基于法布里-珀罗干涉的双电机转速测量

苏 皓,刘冬冬,董太极,高 彪

(东北石油大学电气信息工程学院,黑龙江 大庆 163318)

1 引 言

随着汽车、机器人、机械加工等各种工业应用的发展,对电机的需求越来越大,多电机转速测量越来越受到重视。因此,双转速测量结构被广泛应用于双转子航空发动机振动故障模拟试验台的设计、双电机无级调速耦合传动试验台的设计以及火电厂输煤系统的设计。

速度测量一般采用多普勒频移技术和散斑干涉技术。多普勒频移通常与物体的速度成线性关系,因此可以通过测量多普勒频移来测量物体的速度[1-3]。该方法可以测量转速,相对误差小于5 %,但是多普勒频移法需要考虑激光与物体之间的角度,物体的速度越高,对采样率的要求就越高。散斑干涉是指当照射在漫反射表面的相干光被表面散射时出现散斑并呈粒状干涉结构[4-9],当目标移动,散斑图案将相应地以成比例的速度移动[10],它是一种干涉的一种典型现象。借助于散斑特征,不仅可以研究粗糙表面本身的特征,还可以研究其形状和位置的变化。散斑测量具有非接触、无损的优点。它广泛应用于机械测量[11],信息处理[12-14]和天文学[15-16]。在激光散斑速度测量领域,通过分析散斑信号的统计特性可以容易地实现速度测量[17-20]。参考文献[21]建立了一个紧凑的散斑调制光纤调Q谐振器系统,利用散斑信号的平均频率与旋转速度间的线性相关,实现了实时速度测量。但是计算方法比较复杂。此外,参考文献[18]介绍了基于自相关算法的半导体自混合散斑测速系统。该方法不需要线性拟合,可用于低采样率的高速测量,相对误差小于0.5 %。然而,半导体激光器抗电磁干扰能力弱,抗噪声性能差。与传统的散斑速度测量相比,法布里-珀罗干涉传感器精确、简单、通用、灵敏,并且不受环境噪声的影响[22]。

鉴于此,本文提出了一种基于全光纤法布里-珀罗散斑干涉(Fabry-Perot Speckle Interferometer,FPSI)的新型测速结构。该装置利用一个耦合器和两个环行器将激光分成两个独立、无干扰的测量臂,然后形成两个F-P散斑测速结构,在单个分布反馈激光源(Distributed Feedback,DFB)下完成双测速。利用自相关计算可以得到相应的延迟,结合物体的周长可以测量对应速度[18,23-24]。该结构不仅具有恶劣条件下传输可靠、结构紧凑的优点,而且可以用单个光源独立测量两个旋转物体的速度。因此,所提出的方法具有低采样率,并且是有效的、简单的、精确的、实现廉价的和非接触的测量。

2 理论分析

法布里-珀罗干涉仪的特点是采用单根光纤进行多光束干涉传感。在光纤传输过程中,腔体可以由光纤端面和转轴端面组成,该实验的转轴为鼠笼式三相异步电机的转轴,表面粗糙,从而形成多次反射,如图1所示。当激光束通过耦合器照射到表面时,耦合器的端面会发生反射。当系统稳定时,由于光纤端面的反射率很小,FPSI近似等于双光束干涉。当FPSI发生时,光电探测器接收散斑干涉功率。当电机转动时,FPSI信号反映了电机的运动信息,通过分析FPSI信号可以得到测量转速。在这项研究中,F-P腔结合惠更斯-菲涅耳原理,被用来描述FPSI。

在图1中,re为光纤端面的反射系数；rs为目标物体的反射系数,Se为光纤端面,L为干涉信号传输距离；ω表示旋转对象的角速度；D表示光纤端面和对象之间的距离;S为被测物体。

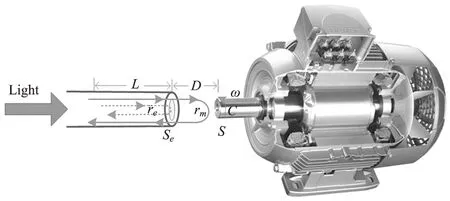
图1 FPI干涉原理图Fig.1 Schematic diagram of FPI

当光经过一根光纤发射到一个物体时,光纤端面Se与物体S等效一个反射面,其反射系数为:

(1)

|rm|=re(1+βcosφ)

(2)

(3)

式中，A表示激光照射到物体粗糙表面所引起的光波幅值；φ表示相位变化；γ表示耦合系数。利用惠更斯-菲涅耳原理描述了反馈光的振幅和相位。

(4)

式中，ψ(x,y) 表示干涉波,r表示从透镜入口处沿光轴方向的一点到物体的距离,r0为测量目标反射系数,k是波束,A=|ψ(x,y)|(0,0)| 和φ=Arg|ψ(x,y)|(0,0)|表示携带物体信息散斑信号的振幅和相位。由于φ=ωt+φ,输出功率为:

(5)

其中,t为一束光经过粗糙物体上的一点并反射回光纤端面的时间,φ为两束光的初始相位,根据公式(5),通过分析输出功率可以获得FPSI所携带物体的信息。当光束照射到物体的一点时,经过一个旋转周期后,返回到光纤端面形成散斑干涉,此时光电探测器(Photodetector,PD)接收到的散斑输出功率:

(6)

其中，t=2D/c为光在外腔的传播时间；c为光速；φ(τ1) 为物体表面的周期性随机散斑信号。利用输出功率的自相关算法,得到该点在经过一个旋转周期后返回光纤端面时的最大值,函数可以表示为:

R(τ)=E[P(τ1)·P(τ1-τ)]

(7)

其中,τ为一个旋转周期的时延,由式(6)和式(7)可得:

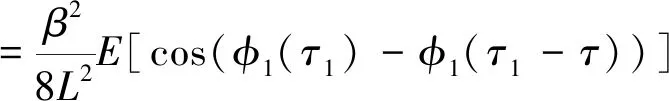
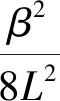
cos(φ1(τ1)-φ1(τ1-τ))]

(8)

由于激光频率2ω超过PD的响应带宽,因此散斑信号的自相关可以表示为:

(9)

当满足φ1(τ1-kΔτ)=φ1(τ1) 和τ=k·Δτ时,利用散斑信号的自相关系数来获取相对最大值,t为一个旋转周期,当k=1,τ=Δτ时,自相关系数达到绝对最大值,得到旋转速度ω:

(10)

其中,C为旋转物体的周长。

3 实验装置与结果

基于双路全光纤法布里-珀罗散斑干涉方法的实验装置图如图2所示。在这个实验中,分布反馈激光器内部有一个40 dB的隔离器,以确保反射的激光不返回激光腔,光源波长为1550 nm,输出功率为2 mW。3 dB耦合器功率比为50∶50,为4端口耦合器。这两个环形器是相同的3端口环形器并具有这样的特性,其中发射到端口1的光将从端口2射出,并且发射到端口2的光将从端口3射出,光不能在环形器中直接从端口1传输到端口3处。由于这一特性,两个散斑信号不会回到激光腔内同时也不相互干扰。在该实验中,两个透镜到每一个到电机的距离不需要完全相等。电机的速度由变频器控制。当光束通过耦合器垂直照射到电机转轴表面并发生反射时,光纤端面与电机之间的距离约为1～2 cm。两个外置PD收集两个旋转电机的散斑信号,这些信号被放大并传输到连接到电脑的数据采集卡,然后数据采集卡将模拟信号转换成数字信号。此外,电机装配有编码器,为实验提供参考速度。

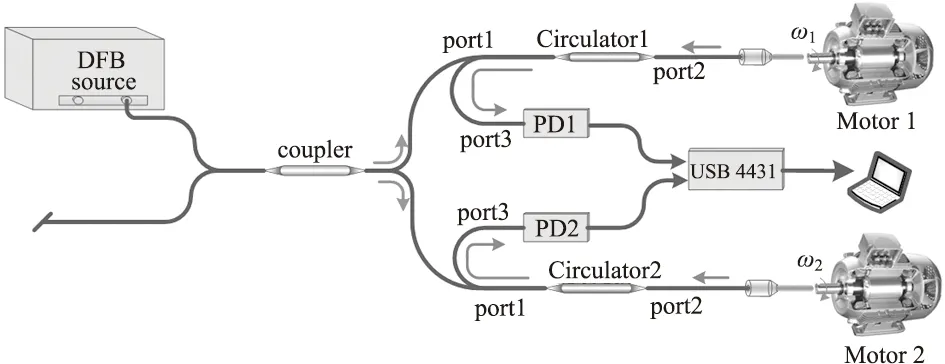
图2 实验装置图Fig.2 Schematic of the diagram experimental setup

对数据采集卡采集的信息进行处理,获得携带速度信息的散斑信号；然后对散斑信号进行自相关运算,得到相关系数最大点的时间延迟；最后根据公式(10)将运动时延与一个周期的运动所经历的距离相结合来获得被测旋转轴的速度。

在实验中,FPSI的自相关方法被用来获得准确的时间延迟。当物体的一个点被激光照射并在一个旋转周期后返回激光腔时,自相关系数达到最大值,得到时间延迟。PD1和PD2分别检测两个电机的散斑信号。如图3所示,由实验测得的散斑干涉信号,图3(a)代表由PD1产生的信号波形,图3(b)代表由PD2产生的信号波形。

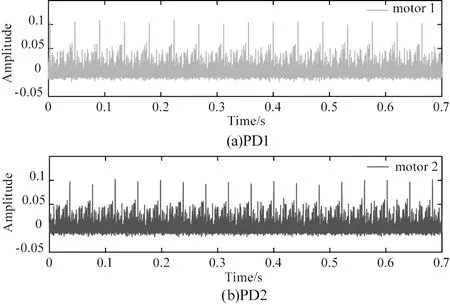
图3 实验测得的散斑干涉信号Fig.3 The speckle interference signal measured by the experiment

此外,图4(a)、(b)为旋转参考速度分别为1361 r/min和1486 r/min时的自相关函数图。在该图中,当自相关数分别达到最大值时,时间延迟分别为0.04412 s和0.04042 s。根据公式(10)便可测量旋转电机的速度。通过计算所得转速分别为1359.93 r/min和1484.41 r/min,最大相对误差分别为0.079 %和0.11 %。

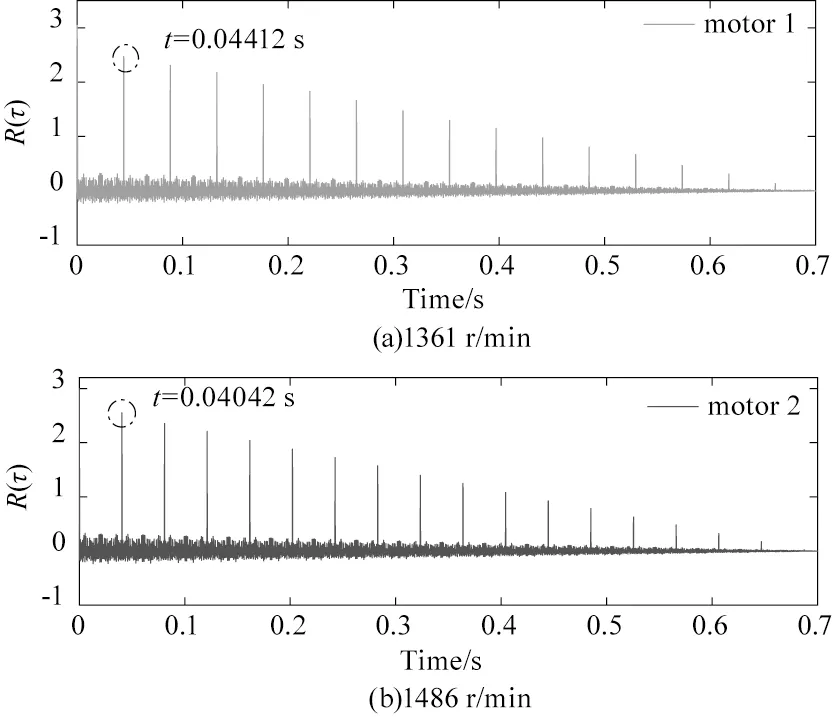
图4 参考转速在1361 r/min和1486 r/min时各自的自相关函数图Fig.4.The respective autocorrelation function diagram of reference rotary velocity at 1361 rpm and 1486 rpm

本文为鼠笼式三相异步电动机提供了一个可调节频率的变频器。通过从低到高调节频率,旋转速度稳定增加。两个物体的随机速度也可以近似相等。调节两电机频率使两个速度分别如下:150和1500 r/min、300和1486 r/min、450和1482 r/min、600和1472 r/min、750和1468 r/min、900和1454 r/min、1050和1447 r/min、1200和1436 r/min、1350和1407 r/min以及1500和1361 r/min。在上述参考速度下每组分别进行了十次实验。图5显示了三相鼠笼式电动机在不同速度水平下的最大相对误差,其中第一电机和第二电机对应的最大相对误差分别为0.23 %和0.14 %。

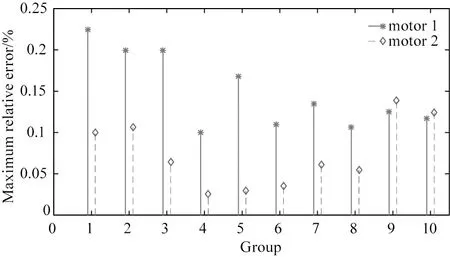
图5 不同速度下的最大相对误差Fig.5.Maximum relative error errors at different velocities

为了验证实验装置的稳定性和可靠性,我们创建了误差棒(errorbar)曲线,如图6所示。误差条的长度代表速度的总不确定度,小于0.0047。

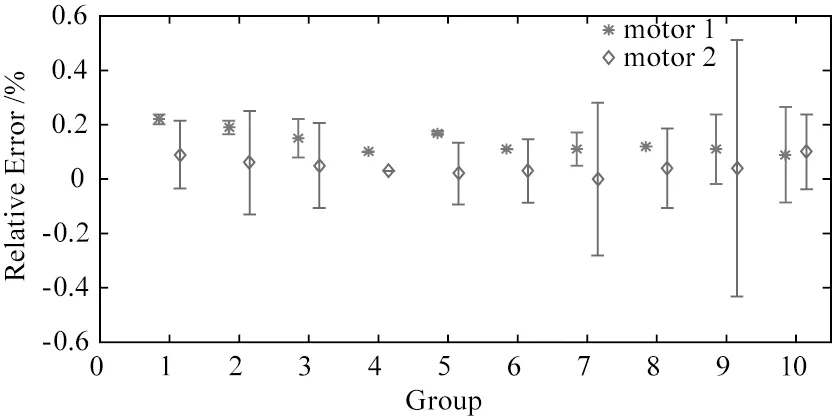
图6 不同速度下的相对误差线Fig.6 Relative error bars at different velocities

为了使实验更精确,进行了六个不同速度的平行实验。以每个平行实验的相同速度对每组数据进行五个重复实验。两个物体的散斑信号相互独立。如表1所示,速度测量的最大绝对误差约为1.75 r/min,测量误差的标准偏差低于1.16 r/min。

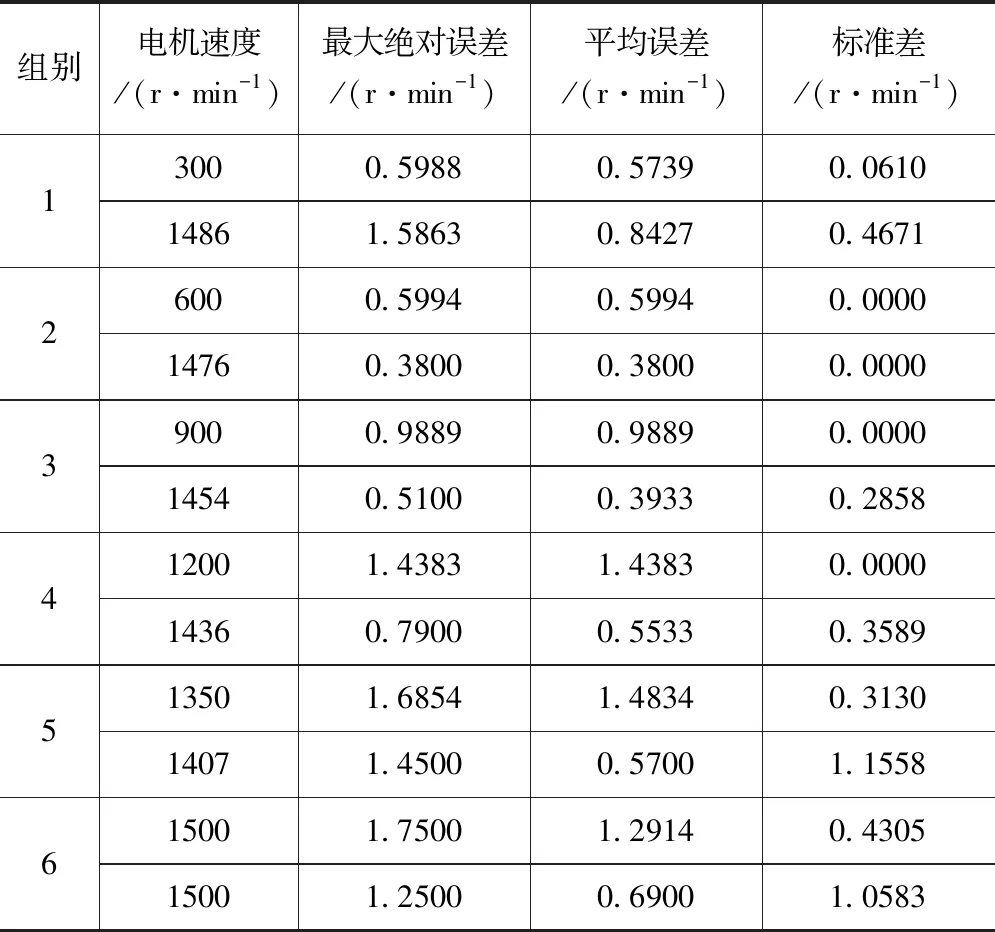
表1 真实速度和实测速度的误差分析Tab.1 Error analysis of real and measured velocities

4 结 论

综上所述,本文使用单个光源实现测量两个电机的速度参数,基于全光纤法布里-珀罗散斑干涉的双电机速度测量方法,减少了实验设备的数量和必要的成本。实验结果表明,该结构利用自相关算法对散斑信号进行分析并且能够准确地同时测量两个电机速度,测量速度的最大相对误差为0.23 %。与传统的速度测量方法相比,该方法的相对测量误差较小。