基于有限元研究传感器位置对矩张量反演方法精度影响
2022-01-11陈致名余艺萌
陈致名,余艺萌
(中国飞行试验研究院,陕西 西安 710089)
0 引言
Gilbert[1]在20世纪70年代提出了矩张量这一物理概念,可以通过矩张量理论相关公式推导出地震时地下天然裂纹开裂后辐射出压缩弹性波的信息。矩张量不仅可以描述天然地震的开裂模型,还可以在地下爆炸等领域描述爆炸点源体积的快速膨胀及由于传播介质相变导致的爆炸点源体积的快速坍塌[2]。Ohtsu[3]在20世纪90年代尝试将矩张量反演理论与声发射试验相结合,利用传感器数据获得裂纹开裂机制,但在声发射试验研究中,对裂纹开裂机制的研究遇到了问题。不过随着相关技术的进步,传感器精度有了明显提高,将声发射试验和矩张量反演理论相结合的相关研究也重回研究学者的视线内[4]。Aki[5]等研究了从震源开裂形成弹性压缩波到传感器接收波动数据并分析处理、反演计算的整个过程。
目前矩张量源的研究也引起了相关学者的兴趣[6],在用矩张量等效体现震源的动力学特性之后,仅需远场假设,整体位移就可以由远场位移替代,远场位移和矩张量之间保持线性关系。地震观测中,采用初至波幅值进行反演计算求得震源开裂机制的等效矩张量时,要求有数个位置合理的台站可以提供台站数据,受条件因素影响,无法布置合理位置的台站时,需要从位置不佳的台站获得数据[7]。利用声发射技术模拟岩石裂纹开裂时,采用矩张量反演理论不仅可以得到岩石内部裂纹面的时空演化机制,而且可以详细描述裂纹面开裂信息,从而掌握不同裂纹开裂时裂纹之间互相干扰、互相影响的规律及单个裂纹扩展或裂纹之间互相穿透的机制[8]。
近年来矩张量反演理论更多的应用在水力压裂、岩体工程、地下采矿等许多领域,并且在以上介绍的不同场景下,矩张量反演理论与不同实际情况相结合,有了更长足的发展[9-11]。在实际工程中,常在裂纹附近位置均匀布置传感器,对矩张量反演计算结果的精度也无法定量判断;而在飞机结构中,结构间存在互相干涉且局部可能存在大量铆钉,由于复材与金属结构的共同存在,材料参数也极为复杂,利用均匀布置的传感器矩张量反演结果精度未必可以得到保证。目前并没有成熟的方法用来判断复杂结构下最优传感器位置,本文将有限元计算与矩张量反演相结合,提出了一种有效判断传感器最优布置位置及矩张量反演精度的方法。
1 研究方法
1.1 矩张量理论和矩张量反演理论
矩张量的物理意义是,一个微裂纹开裂的动力学特性可以等效为在一个微体积元上加载力矩。而这个受载的微体积元其上分布的等效载荷依方向可分为9个力矩,将9个力矩按顺序组合成矩阵,该矩阵即为矩张量,形式如下:
(1)
式中,右侧矩阵内的分量mij为对应震源的等效矩张量分量。当i与j相同时,mij代表法向力矩;当i与j不同时,mij代表切向力矩。
裂纹开裂时的动力学状态与矩张量元素之间互相等效,公式如下:
mpq=λvk[uk(ξ,τ)]δpq+μ(vp[uq(ξ,τ)]+vq[up(ξ,τ)])
(2)
式中:mpq为矩张量元素(不同方向的等效力矩);λ、μ为拉梅常数(可由E、σ导出);ui为裂纹面的法向向量;vi为裂纹面的位移向量;δpq为狄拉克雷函数。
基于震源的波动论和点源假设,引入格林函数,把矩张量与传感器收集到的数据联系起来。传感器k接收到的波形位移振幅uk应为:
uk(x,t)=Gki,j(x,t;ξ,t′)Mij(ξ,t′)
(3)
式中:*为卷积符号;Gki(x,t;ξ,t′)为弹性动力学格林函数,是由单位脉冲集中力引起的位移场,即震源(ξ,t′)和监测端(x,t)之间介质的脉冲响应;Mij(ξ,t′)为3×3大小的矩张量矩阵。
公式(3)中Green函数的解为弹性波位移场,可以依据监测端与裂纹中心距离的不同,将裂纹开裂辐射后的弹性波位移场的三个分量分别表示为近场项、中场项以及远场项。当传感器的位置与裂纹较远时,近场项与中场项相比于远场项足够小,可以将这两项弹性波位移场的分量忽略,这个距离条件也被成为远场条件。
当监测端与裂纹之间的距离符合远场条件时,矩张量反演公式可以简化为下式:
(4)
式(4)为三维空间下的矩张量反演公式。由于本文的研究内容范围为二维空间,因此需将此方程进一步简化:
(5)

1.2 有限元计算内容
在有限元计算过程中,需要构造一个简单的裂纹模型,筛选出符合远场条件的节点编号,再求出裂纹开裂后以上节点的初至波幅值,将幅值带入矩张量反演计算,通过对比得到最优的传感器布置位置。
本文选用物理模型为半径400 mm的圆,将传感器布置在半径300 mm的圆上,点源设置在正中心,传感器与点源距离大于波长的8倍,满足远场条件(由于飞机上被监测结构之间形状差别很大,因此模型的形状并无具体要求,只需满足传感器的布置条件即可,模型具体形状依据划分网格的方式而定)。
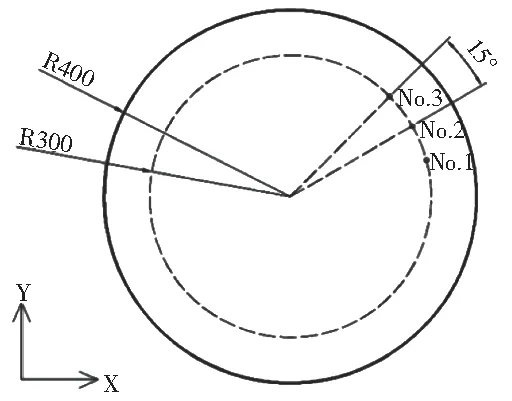
图1 物理模型
图1为一种物理模型示意图。
由于裂纹开裂过程为动态受载,整个加载过程中力的变化类似于阶跃载荷。因此在有限元建模时对裂纹面施加强制位移来模拟裂纹的断裂过程,经归一化处理,强制位移的最大值设为1,加载点的强制位移与时间的函数关系如式(6)所示:
(6)
式中:Tr为半周期长,时间到达Tr时位移的幅值达到峰值。强制位移-时间函数图如图2所示。
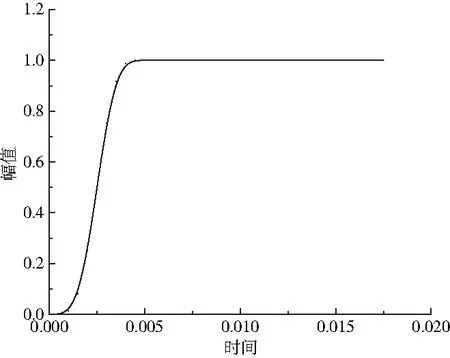
图2 强制位移-时间函数图
首先将有限元计算结果整理成极坐标的形式与理论结果比较,其后从所有符合条件的节点中任取三个节点反演计算出点源矩张量,将其与设定值进行对比,利用蒙特卡洛方法进行大量重复试验,从众多样本中筛选出一系列使计算结果误差最小的传感器布置组合,将每个组合连线成三角形,并画在一张图上,就可以最优的传感器布置位置的分布方式,同时把得到最优传感器组合的样本数与总样本数进行比较,比值的高低可视为反演精度的高低。
得到反演矩张量后,需要对其精度进行判断,本文给出一种判断方法:首先通过矩张量反演计算从有限元计算结果中得到计算矩张量,将其进行归一化处理,分别计算该矩阵与有限元建模时的加载等效矩张量的Frobenius范数,将两范数比较得到误差,同时还需比较计算矩张量矩阵与加载等效矩张量矩阵的主元素大小差别,最后只有当范数误差与主元素误差同时小于一定程度时,才可以将该组合视为最优组合。
2 简单模型计算结果
分别采用四节点四边形单元和三节点三角形单元两种有限元网格划分形式分析矩张量反演问题,并比较了两种简单裂纹模型的精度区别。
模型材料参数设定为:E=5.4 GPa,σ=0.2,ρ=3000 kg/m3。
裂纹的构造方式为在同一位置放置两个节点,两点之间不作约束,同时对两个节点施加方向不同的强制位移。
2.1 拉伸裂纹模型
2.1.1 模型介绍


(7)
2.1.2 计算验证
首先整理所需节点编号,在NASTRAN中导出所有节点的位移文件后,提取初至波峰值,同时利用矩张量反演公式,可以求得任意节点的理论初至波峰值,将两者以极坐标的形式进行比较并归一化。
由图3和图4可知,对于拉伸裂纹来说,三角形网格的计算结果与理论结果吻合效果较好,整体无较大计算误差。

图3 四边形网格对比图 图4 三角形网格对比图
2.2 剪切裂纹模型
2.2.1 模型介绍

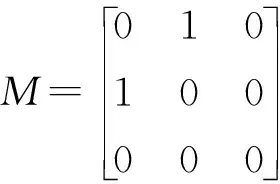
(8)
2.2.2 计算验证
计算初至波峰值与理论初至波峰值比较图如图5和图6所示。
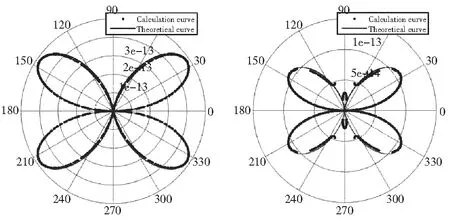
图5 三角形网格对比图 图6 四边形网格对比图
由图5和图6可知,对于剪切裂纹来说,三角形网格的计算结果与理论结果吻合效果较好,整体无较大计算误差。
2.3 总结
矩张量反演问题与常规裂纹计算问题不同,矩张量反演问题关注不同方向幅值的相对大小,而不是有限元计算结果与真实结果之间的绝对大小。三角形单元作为常应变单元计算精度较低,但是其在单元的不同边上计算位移与真实位移之间的误差近似,误差的空间分布更平均,因此用三角形单元有可能会得到更好的矩张量计算结果。
两种裂纹的理论幅值与计算幅值的拟合效果都很好。而由于拉伸裂纹的幅值形状为双页,剪切裂纹的幅值形状为四页,双页形状变化更便于观察,因此在分析材料属性及材料缺陷产生的影响时,选择拉伸裂纹模型。
3 材料参数的影响
本章分析材料参数对反演精度产生的影响,将不同材料参数导入模型进行矩张量反演计算,分析矩张量反演方法应用于各种不同材料时的精度变化。

3.1 泊松比
分别对不同泊松比模型分析计算,比较各个模型符合反演精度的最优组合占比。

表1 反演精度随泊松比变化
泊松比为0.2时最优组合分布如图7所示(将每个最优组合用三角形表示)。
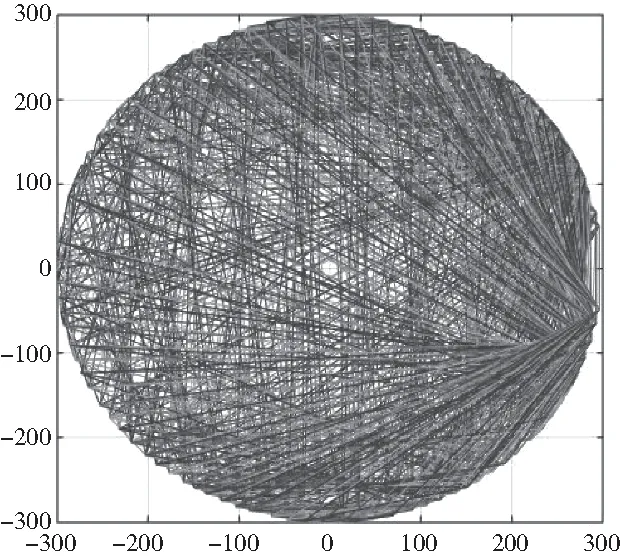
图7 泊松比为0.2时最优组合分布图
可得最优组合的位置分布并无明显规律,理想拉伸裂纹模型的最优传感器选择受较低限制,最优组合占比低于100%的原因是筛除掉了传感器位置较近的传感器组合,且将最优组合的误差条件设置得较高。
由于泊松比影响较小,因此有限元计算时,不用过多考虑泊松比的变化对反演精度的影响。
3.2 弹性模量
分别对不同弹性模量的模型分析计算,比较各个模型符合反演精度的最优组合占比。

表2 反演精度随弹性模量变化
随着弹性模量的变化,反演精度变化较小。当弹性模量变大时,最优组合数量占比略为减小。
3.3 复合材料的适用性
选用两种复合材料进行分析计算,两种复合材料的材料参数见表3,幅值比较图如图8和图9所示。

表3 两种复合材料的材料参数
由图8和图9可知,两种复合材料的计算与理论幅值曲线图相差不大,其最优组合占比见表4。
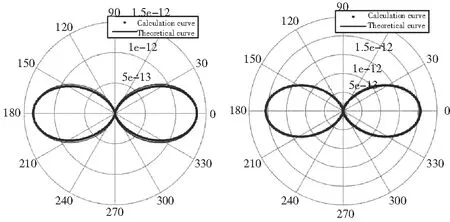
图8 复材1对比图 图9 复材2对比图

表4 不同各向异性材料的最优组合占比
复材1的最优组合分布如图10所示。
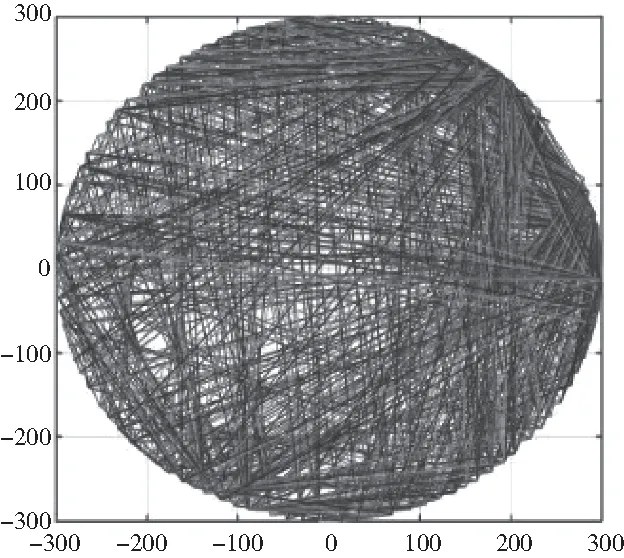
图10 复材1的最优组合分布
可得以上两种复合材料与理想模型相比反演精度差别较小,且最优传感器位置分布规律并未因材料为复合材料而发生明显变化,即对于常见的复合材料矩张量反演计算时,不需要特意调整传感器布置位置。
4 结论
1)有限元方法配合蒙特卡罗方法可以有效辅助矩张量反演问题的计算,筛选总结出最优传感器位置;
2)有限元模型网格划分形式对矩张量反演计算结果的影响较大,单元精度的空间均匀性比绝对大小更重要;
3)简单模型的最优传感器位置几乎不受材料参数影响,对于飞机的复杂结构(如多条裂纹同时开裂、局部存在多个铆钉、结构存在孔隙及孔洞等),可通过本文提出的方法有效判断其传感器的最优位置。
