一种微棱镜角度误差测量系统的研究与应用

郗鸿振，娄志峰，钱 钧，任伟鹏，张忠宁

(大连理工大学机械工程学院，辽宁 大连 116000)

0 引言

反光膜的作用是把照射在其上的入射光线反射出来，且出射光线与入射光线平行且反向，在城市和道路交通中的应用非常广泛[1]。高等级微棱镜反光膜的制作对反光膜材料、模具和制作工艺都提出了很高的要求，尤其是反光膜模具微棱镜结构的表面粗糙度和角度精度。随着国内市场对高等级微棱镜反光膜的需求增加，迫切需要提出新的微棱镜角度误差测量方法以改善其角度精度。反光膜内部的微棱镜反光阵列实际为正三棱锥结构，在实际工业生产中对于具有正三棱锥结构的棱镜，对其三直角面间夹角的角度误差的测量通常有两种方法。一是使用精密测量仪器直接检测角度误差，其优点是可以准确直接地测量棱镜的被测参数，缺点是检测效率慢，不适合快速测量。二是搭建光学测量系统进行检测，其主要优点是测量系统简单易于搭建，且操作简单，缺点是光学测量系统误差影响因素较多，需分析各种误差来源[2-5]。对于尺寸较小的微棱镜，国内微棱镜反光膜生产商主要采用常规共聚焦显微镜图像识别的方法测量微棱镜的角度误差，但此方法检测效率过低，很难达到实际的测量需求。因此，提出一套快速准确的微棱镜角度误差测量方法对制作高性能微棱镜反光膜具有重要意义。

本文基于角锥棱镜角度误差的测量原理，结合微棱镜的反光原理和结构特点，先建立微棱镜角度误差的光学测量模型，并搭建基于自准直测量原理的光学测量系统完成对微棱镜角度误差的测量。在测量实验前对测量装置进行灵敏度标定实验与稳定性测量实验，实验数据表明该测量系统精度较高，可用于微棱镜角度误差的测量。最后利用该测量系统可快速实现对微棱镜反光阵列角度误差的测量，试验表明，相比于常规共聚焦显微镜图像识别的测量方法，本测量系统测量效率更高。

1 测量原理与方法

1.1 测量原理

微棱镜结构如图1所示。进入微棱镜的一束平行光线，由三棱锥结构的斜面入射，经三个直角面的反射后再次经斜面射出，如果微棱镜是理想棱镜，三直角面之间没有加工误差，则出射光线会与入射光线平行[6-7]，如图2所示。但是由于实际上在生产制作过程中，微棱镜三直角面之间总会存在加工误差，由微棱镜反射后的出射光线不可能与原入射光线完全平行，且二者之间夹角的大小与微棱镜角度加工误差的大小有着直接的关系。通过研究入射光线在微棱镜内部的折射反射规律，结合空间坐标系的矢量关系，建立微棱镜角度误差的光学测量模型。最后通过自准直法测得出射光线与入射光线的夹角，并结合上述数学模型求得微棱镜的角度误差。

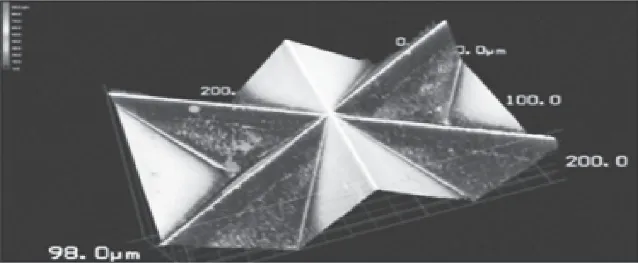
图1 微棱镜结构示意图

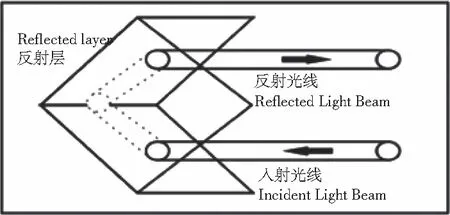
图2 反光原理

1.2 测量方法

精密角度测量普遍采用自准直测量原理[8]，因此入射光与出射光之间的夹角采用自准直仪测量，如图3所示，测量精度可以达到2角秒。

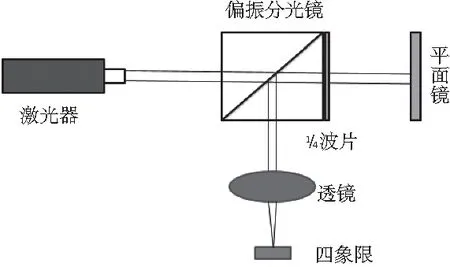
图3 自准直仪光路原理图

1.3 光学测量的数学建模

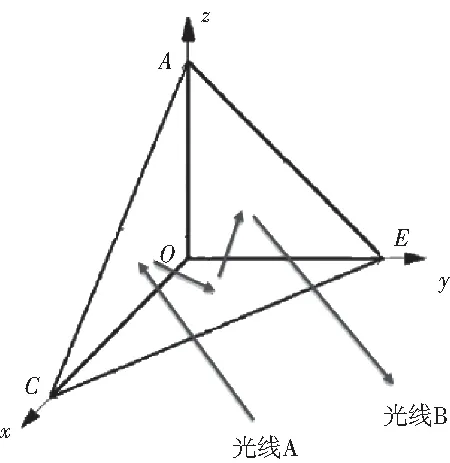
图4 坐标系示意图

对于理想的微棱镜(无角度加工误差)，建立空间直角坐标系，如图4所示。设三直角面之间的角度误差分别为θ12、θ23、θ13。

(1)

1-2nθ13+2nθ23)

(2)

(3)

同理可计算入射光线分别由2、3面入射微棱镜，经2、3、1以及3、1、2面反射后出射光线与入射光线之间的夹角δ2、δ3，最后建立光线夹角δ1、δ2、δ3和角度误差θ12、θ13、θ23关系的数学模型：

(4)

2 实验

2.1 自准直仪的搭建

自准直仪的测量原理是基于光学自准直原理实现的，光学自准直原理主要包括光的准直原理以及平面镜对光束的反射原理[9]。如图5所示。

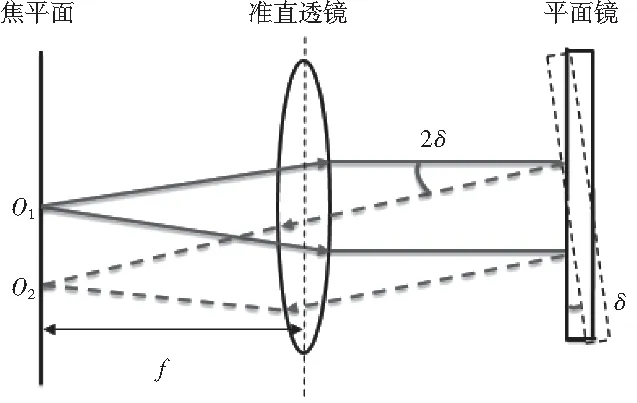
图5 自准直原理图

当准直透镜、平面镜、焦平面与光路垂直时，在O1处(透镜焦点)发射的光束经过准直透镜后形成平行光，平行光经平面镜反射后原路返回，经准直透镜聚焦后在出射点O1处成像；当偏转反射镜一个角度δ时，平行光经反光镜反射后将偏转2δ，经过准直透镜聚焦在O2处成像，这时出射光与入射光之间的夹角同样为2δ；由图中几何原理可求出：

O1O2=ftan2δ

(5)

式中，f为准直透镜的焦距，当偏转角δ为一微小角度时，角度的弧度值约等于正切值，如公式(6)所示[10]。

(6)

图3为自准直仪原理图，主要由激光器、偏振分光镜、聚焦透镜和四象限组成，可以实现小角度的精密测量[9]。光线由激光器发出，经偏振分光镜后照射到平面反射镜上，经过平面镜反射后的光束入射到偏振分光镜中发生反射，然后经聚焦透镜入射到四象限上；当平面反射镜偏转一定角度时，经平面镜反射后的光线会与入射光线形成相应的角度变化，然后经透镜聚焦后在四象限上产生光斑位置的变化，进而可计算得到平面镜的角度偏转值。

2.2 标定实验

图6 标定原理图

四象限探测器输出信号为电流信号，经信号处理电路转换后可获得电压信号，处理后的电压信号与光斑位置的关系需要通过标定实验确定该关系的比例系数K(灵敏度)，所以在测量实验前需要对自准直仪进行标定。自准直仪标定时采用的是AUTOMATD265光电自准直仪，精度0.2角秒，图6为标定原理图。

当角度微调座带动自准直仪和平面镜发生微小角度变化后，光电自准直仪可以准确测量出角度变化值，通过自准直仪的读数和光电自准直仪的读数可实现自准直仪的标定。在±100角秒测量范围内对自准直仪进行标定，自准直仪标定结果及残差图如图7、图8所示，自准直仪偏摆角灵敏度1827.52，标定残差在±1.4角秒以内，俯仰角灵敏度1945.16，标定残差在±1.2角秒以内。

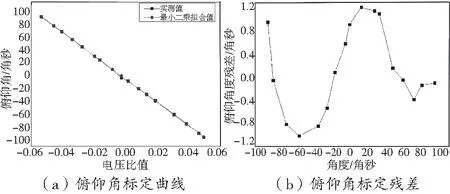
图7 俯仰角标定结果

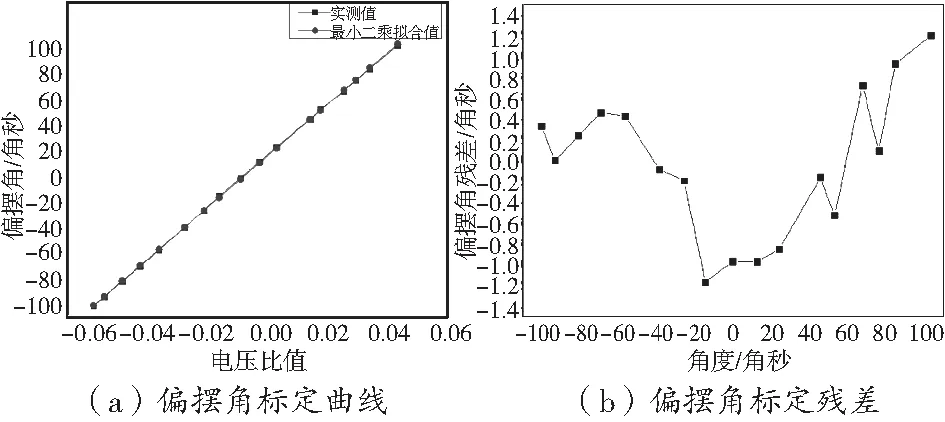
图8 偏摆角标定结果

2.3 稳定型实验

为获得稳定准确的测量数据还需对测量系统的稳定性进行实验验证，分别以1 S/s的采样频率进行40 min的采样零漂实验和以10 S/s的采样频率进行10 s的短时间稳定性实验，零漂曲线和稳定性曲线如图9(a)、(b)所示。由测量结果可知，自准直仪偏摆角和俯仰角在40 min内的漂移量在1.2角秒和0.8角秒以内，在10 s内的数据波动量分别在0.12角秒和0.24角秒内，由稳定性实验结果可知该自准直仪的稳定性较好，可用于角度误差的测量。

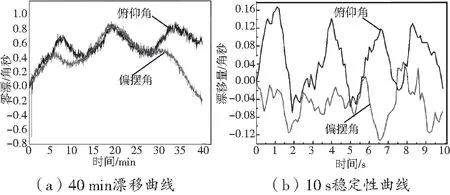
图9 稳定性曲线

2.4 微棱镜角度误差测量实验

本文测量对象为微棱镜反光膜样品，其实物图如图10所示，图11为在光学显微镜下观察到的微棱镜内部结构。

图10 微棱镜反光膜实物图 图11 微棱镜内部结构图

图12 测量装置实物图

本文测量装置实物图如图12所示，测量装置结合数据采集系统以及数据处理系统构成本文微棱镜角度误差的光学测量系统。

表1、表2列出了在相同实验环境下得到的实验测量数据(单位：秒)。

表1 1-10组角度误差测量值与标准值对比

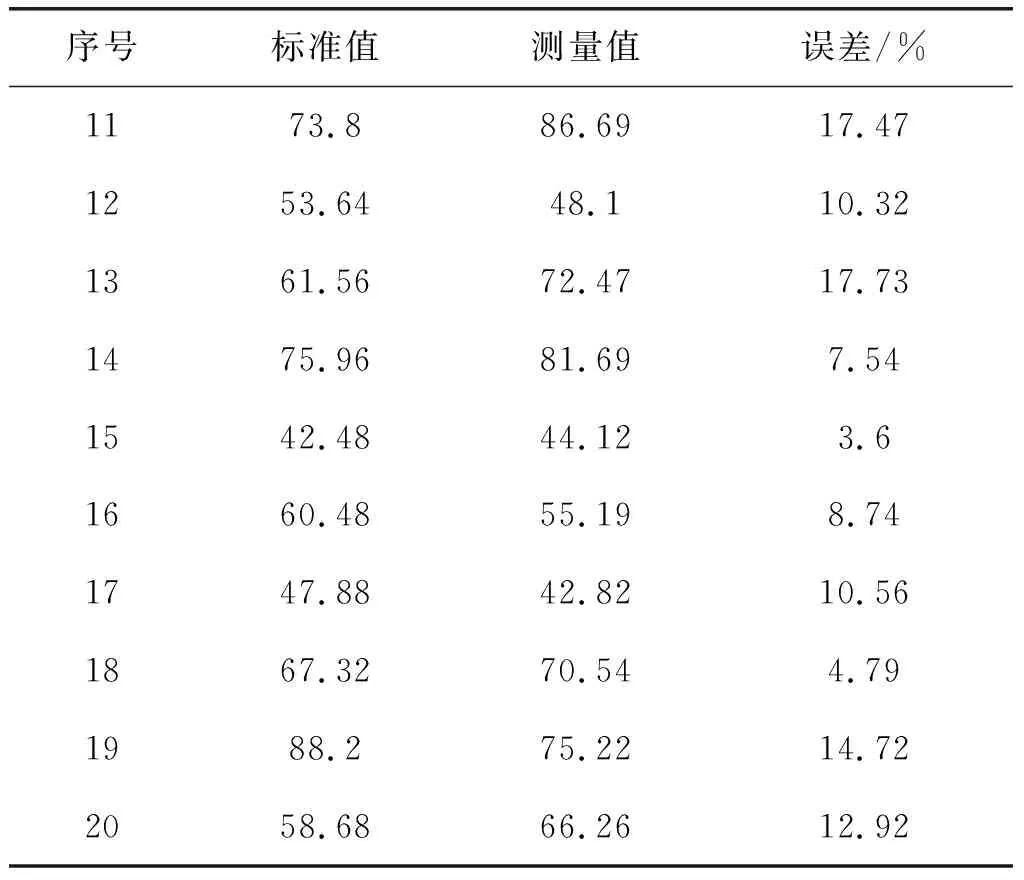
表2 11-20组角度误差测量值与标准值对比表

说明：

①微棱镜由微棱镜反光膜生产商提供；

②标准值是微棱镜反光膜生产商提供的通过激光共聚焦显微镜测得的角度误差；

③测量值表示微棱镜各夹角综合角度误差，其值为三直角面间三个夹角的均方根，由本文开发的测量系统测得。

由检测数据可知，在20组被测数据中，本测量系统测量数据与激光共聚焦显微镜测量数据间的误差小于5%的4个，误差在5%～15%之间的12个，误差大于15%的4个。

3 结论

本文针对微棱镜角度误差共聚焦显微镜测量方法的局限性提出一套基于自准直仪结合光学测量数学模型实现对微棱镜三直角面之间夹角角度误差的测量系统。在测量实验前对测量装置进行灵敏度标定实验与稳定性测量实验，标定残差在±2arcsec以内，稳定性实验表明，测量系统漂移量在±12arcsec以内，该测量系统精度较高，可用于微棱镜角度误差的测量。最后利用该测量系统完成了对微棱镜角度误差的测量实验，实验结果表明，相比于常规共聚焦显微镜图像识别的测量方法，本测量系统测量效率更高，可以满足实际生产中的测量要求。