基于概率预测的电网静态安全运行风险评估及主动调控策略

2022-01-11姜新雄刘志成邹曜坤廖思阳

电力系统自动化 2022年1期

徐浩，姜新雄，刘志成，邹曜坤，廖思阳，徐箭

（1. 国家电网公司华中分部，湖北省武汉市 430077；2. 武汉大学电气与自动化学院，湖北省武汉市 430072）

0 引言

随着特高压交直流混联大电网和可再生能源的快速发展，新能源出力特性给电网带来的影响和挑战日益加剧［1］，电力系统特性发生了深刻变化。电网运行全局监视、全网防控、集中决策的需求日益突出［2］，研究电网主动调度控制（以下简称“调控”）策略是提升调控水平、促进经验型调控向分析型和智能型转变的重要手段［3］。一般来说，面对源荷双重不确定性，现有调控方式仍主要停留在被动控制阶段［4-5］，即等需要调控的场景或故障到来之后再制定策略并实施。然而，此控制方式往往会错过最佳的预先调控时间，无法充分利用调控时间常数较大的资源，使得电网安全处于被动位置［6］。

考虑现有调控方式主动性的不足，若能在调控场景到来之前对其进行预测［7-9］，提前制定策略，便可为系统调节争取更多的资源以及准备时间［10］。目前，这方面的研究主要集中在态势感知［6-11］、暂态稳定评估［12-14］等方面，其评估结果往往是未来电力系统所属的状态类型［15］。然而一般情况下，仅有类型信息难以反映场景的危急程度，无法帮助调度运行人员准确判断局势，导致类别信息起不到理想作用，工作人员依然需要凭自身经验重新判断并制定策略。于是，许多学者开始进行风险预警研究，以此来辅助调度人员进行更精确的决策。

目前，风险评估在电力领域的研究主要集中于概念建立及必要性分析［16-17］、风险指标改进［18-22］以及基于风险的调度决策［23-26］等方面。其通常采用可能性与可靠性并重的模式，其中对可靠性的研究主要集中于严重度建模方面，文献［19］较早提出了风险评估的相关概念，并建立线路过载、电压越限等事件的风险评估指标；文献［20-21］进一步加入设备重载、失负荷等指标，丰富了评估体系。上述研究虽然对严重度进行了建模，但随着大量新能源及电力电子设备的接入，系统动态特性愈加复杂，这类基于确定性假设和模型驱动的风险评估方法已较难准确估计系统真实风险。于是，基于数据驱动的风险评估方法近年来受到了广泛关注［27-32］，但其中大部分仍主要针对数据驱动方式下的指标改进［27］且基于确定性故障进行假设［28］，未涉及各类可能事件的概率获取方法［29-30］。仅有少量研究将场景概率与风险评估相结合［31-32］，如文献［31］采用生成对抗网络来考虑系统各可能事件的概率及对应后果，实现配电网运行风险分级；文献［32］基于迭代随机森林，利用实时数据对系统风险进行动态评估，具有良好的鲁棒性。但上述研究仍局限于对系统当前状态的评估，没有量度未来场景下的风险，也未利用安全风险评估结果指导调控。

因此，本文基于电网中关键变量的时序预测信息，沿用文献［19］提出的电压、潮流等风险指标，并加入对变压器越限事件的考虑，构建典型场景的概率预测模型，输出关键元件在未来时刻的越限概率，计算系统安全风险，从而辅助调度运行人员提前进行系统调控，增强电网安全运行主动性。

1 基于时序预测及支持向量机（SVM）的概率预测模型

本文所提出的安全风险评价模型的评估对象为系统未来的运行状态，需要滚动地对系统关键变量（如新能源发电、负荷功率等）进行超短期时序预测，并将其作为目标场景（指线路过载、电压越限等）概率预测模型的输入，从而得到系统未来各假设场景的概率结果，作为安全风险评价模型的输入，并最终集成为系统量化风险值，从而指导主动调控。本文采用长短期记忆网络（LSTM）对系统关键变量进行超短期时序预测［33］，作为场景概率预测模型的基础。

1.1 SVM 原理介绍

SVM 在电力系统中应用广泛，在暂态稳定评估、变压器故障诊断等方面都展现出了较好的预测性能，具有训练样本少、泛化能力强等特点［34-35］。同时，对于一个任意的样本x，SVM 可以获取其与分类超平面的距离，从而定义分类结果的置信程度，具有概率意义［36］。因此，本文采用SVM 对特定场景的未来状态进行预测。

设有样本集(xi，yi)，i=1，2，…，n，其中xi∈Rm为第i个样本的m维输入特征；yi为样本标签值，值为1 表示线路过载，值为0 表示不过载；n为样本数量。SVM 采用核函数K(xi，x)将原问题映射至高维空间，而后在其内部构造最优分类超平面f(x)，即SVM 决策函数。

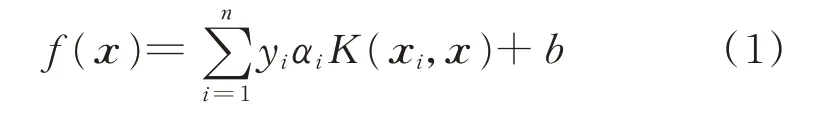
式中:αi为拉格朗日乘子；b∈R 为偏移量。αi可以通过求解式（2）至式（4）的优化问题得到。

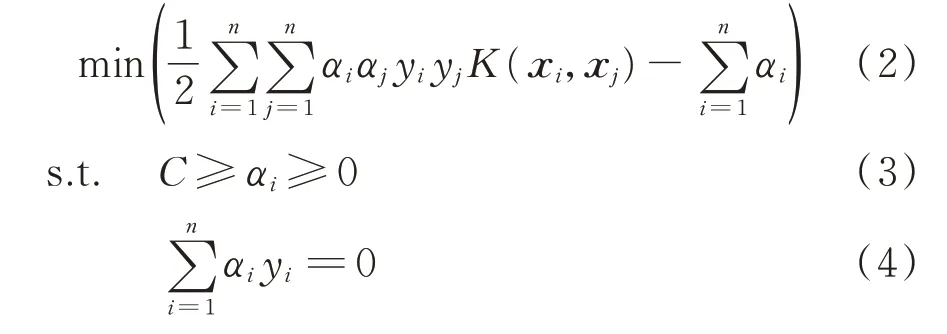
式中:C∈R 为惩罚因子。

核函数K(xi，xj)选用径向基核函数（RBF）［37］:

式中:γ∈R 为核参数；‖ · ‖表示求2 范数函数。一般情况下，可通过网格搜索或启发式算法获取模型的最优参数γ和C。

1.2 SVM 概率输出

如式（1）所示，对于任意一个待分类样本x，决策函数f(x)输出为一确定的数值，即决策分数。在二分类问题中，SVM 可基于决策分数完成类别预测，但决策分数只能反映样本距离分类超平面的远近，而不具有概率形式。采用一个带参数的sigmod函数修改SVM 的输出，可以将其决策函数值映射到区间［0，1］，从而实现概率输出［38］，其形式为:

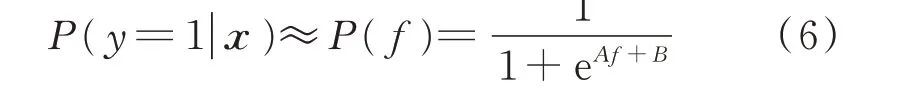
式中:A和B为sigmod 函数参数，可以由决策分数集训练得到［39］；y为样本分类标签值，y=1 表示正例样本；P(y=1|x)代表样本x属于正例的概率；f=f(x)为决策函数。

一个样本集(xi，yi)需要同时训练得到SVM 分类器和参数A、B。为避免过拟合，采取交叉验证的方式，将训练样本集(xi，yi)分为d组，利用其中的d-1 组训练得到SVM 模型，并计算剩下一组样本的决策分数f，如此处理d次便可得到所有样本的决策分数，进而形成sigmod 函数参数训练数据集(fi，yi)。求解参数A、B的具体过程如下。

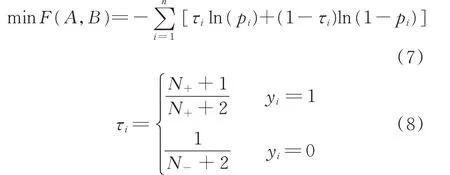
式中:pi=P(fi)为对应第i个样本为正例的概率估计；N+为全部样本中正例的个数；N-为全部样本中负例的个数。上述方法得到的概率输出实际上是模型决策分数的另一种表现形式，是在统计意义下对决策分数的最优映射，而后者直接决定了模型的分类表现。因此，概率预测的准确与否实际上也可从模型的分类表现得到体现。

概率估计能够反映待识别样本x属于不同类别的概率，有效地对样本与分类超平面的距离进行归一化，对一个常见的二分类问题，概率输出pi在0%～100%之间。除了分类模型给出的预测标签外，概率输出提供了更多信息，使相关人员对电网未来态势有更加全面的了解。具体地说，对于一个线路是否重载的场景，基于系统可观测变量，分类模型可以给出下一时刻该线路是否重载的预测结果，而概率预测模型则可以输出该线路在下一时刻重载概率值，从而辅助调度人员做出更加全面的判断和分析。同时，该概率输出也将作为安全风险评估模型的输入及量化系统风险值的基础。

1.3 SVM 多分类概率输出

实际上，电力系统中存在的绝大多数预测问题属于多分类问题，二分类模型通常难以表示系统元件或者态势的完整状态［28］，如一条线路在其负载率超过重载阈值之后便属于重载线路，但重载的严重程度却无法表述出来。通常期望获取的不仅仅是变量的二分类信息，而是变量处于某个范围或者超出某个阈值多少之类的信息。因此，本文将电力系统目标场景分类模型扩展至多分类模型，同时计算各假设场景的多分类概率输出作为安全风险评估模型的输入，为调度运行人员提供全面精准的辅助信息。

2 考虑风险评估的电网主动调控模型

风险评估的意义在于将以往只能定性分析或根据运行经验判断的电网场景和事件予以量化，从而更加明了地评估风险大小。本章依据上文介绍的概率预测方法，构建考虑关键对象越限概率的风险量化指标，作为电网主动调控的触发指令。

2.1 考虑裕度的电网稳定性风险评估

整体上，风险评估包括事件发生的可能性和事件的严重性，其定义如下。

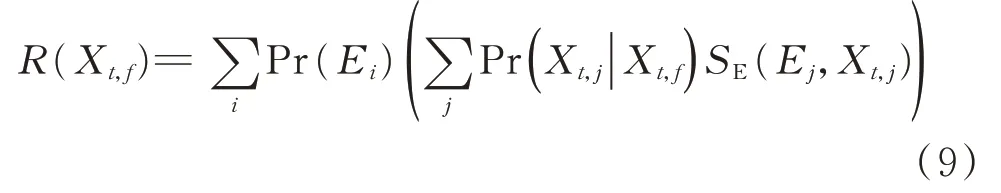
式中:Xt，f为t时刻的预测运行方式；Xt，j为t时刻的第j种负荷情况；R(Xt，f)表示系统在运行方式Xt，f下的量化风险大小；Ei为第i个场景；Pr(·)表示场景发生的概率；SE(Ej，Xt，j)为第j个场景的严重度函数。从式（9）可以看出，t时刻系统的运行风险是各个场景的概率与其后果的乘积之和，从数学本质上来讲是t时刻在预测的运行方式下全场景后果严重度的期望值。

从式（9）可以明确风险评估主要分为3 个步骤，即目标场景的假设、对目标场景进行概率分析以及后果分析。其中，目标场景可以依据实际的工程应用需求和网络特点进行合理假设（如线路过载、节点电压越限等），针对特定场景的概率分析可通过上文所述的基于时序预测的概率预测模型完成，因而对场景后果的分析即严重度函数的构建成为本节的重点。确定场景后进行后果分析一般有2 个步骤，即选择严重度函数和对严重度函数进行计算。关于严重度函数的选择，除传统的安全性评估外，考察系统充裕度的风险评估方式在近年来也愈发被重视。充裕度是指系统各设施在其额定容量以及电压波动的允许范围内，考虑计划和非计划停运等各种约束下持续向用户供电的能力［19］，从充裕度角度进行计算可以描述系统可接受风险的范围和当前系统状态与崩溃点之间的距离。

本文基于严重度函数建立应遵循的6 个原则［19］，分别从电压稳定性、线路潮流、变压器运行状况等角度建立稳定性裕度表达式并建立相应风险指标如下。

1）电压越限事件严重度函数

式中:Vlim为电压限值，在计算不同指标时可分别取电压上限Vmax或下限Vmin；Vk为事件k发生时的电压标幺值；Svolt，k为电压越限事件k的严重度。

2）线路过载事件严重度函数

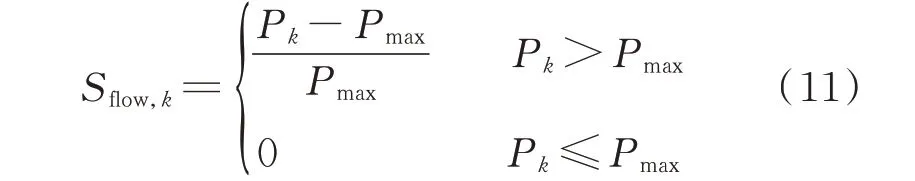
式中:Pmax为线路潮流安全限值；Pk为事件k发生时线路潮流标幺值；Sflow，k为线路过载事件k的严重度。

3）变压器越限事件严重度函数

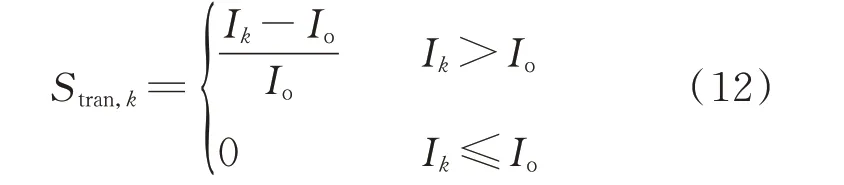
式中:Ik为事件k发生时变压器电流；Io为变压器重载运行判据，一般取额定电流的70%；Stran，k为变压器越限事件k的严重度。

在上述严重度函数的计算式中不难发现，Svolt，k、Sflow，k、Stran，k均无量纲，若直接将不同种类风险值相加可能会出现遮蔽现象［18］，故需要对严重度函数的计算结果按式（13）进行归一化处理。

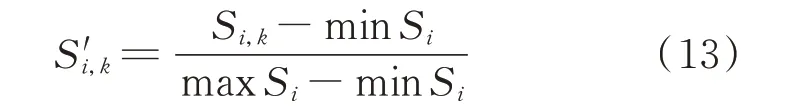
式中:Si，k为第i类事件中第k个事件的严重度；S′i，k为归一化后第i类事件中第k个事件的严重度；Si为第i类事件的严重度。式（13）表达的含义为对每一类事件（如电压越限事件）分别按其最大、最小值进行归一化处理。

采用层次分析法［40-41］计算电压越限事件、线路过载事件、变压器越限事件权重ωvolt、ωflow、ωtran，分别为0.17、0.17、0.66。将归一化处理后的严重度函数计算结果进行加权求和即可评估全网风险，根据电网的实际运行情况可以设定阈值以判断风险能否接受；若无法接受则根据下文提出的策略下发指令进行优化调控。

2.2 基于风险评估的主动调控策略

如上所述，主动调控实质上是在每一时刻滚动对未来一定时间段内的运行场景进行风险评估，在系统即将面临重大风险时提前下发调度指令，改变系统运行方式以避免发生安全事故，其架构如图1所示。

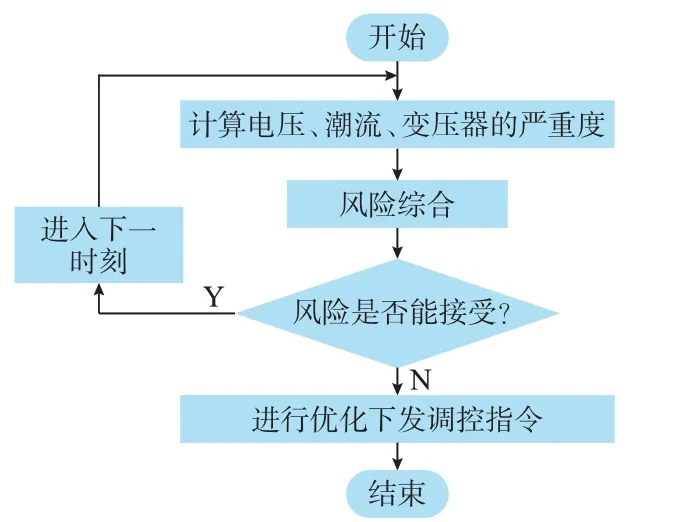
图1 滚动安全风险评估体系架构Fig.1 Architecture of rolling security risk assessment

在降低系统运行风险的优化模型中，考虑在传统经济调度常规约束基础上加入风险函数作为不等式约束，以此确保预防控制策略的执行能使系统安全充裕度得到提高。以调节成本最小为目标函数，即

机组运行成本函数为:

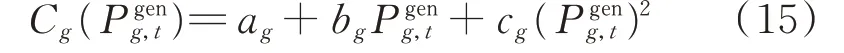
式中:ag、bg、cg为发电机g的燃料成本系数。

1）发电-负荷平衡约束

4）线路潮流极限约束

5）风险约束

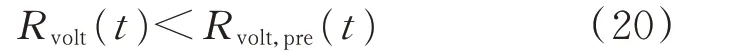
式中:Rvolt(t)为按预定调度指令动作后时刻t电网中电压事件风险；Rvolt，pre(t)为预测电压风险。风险的计算方法如上文所述为同类事件的严重度期望之和。

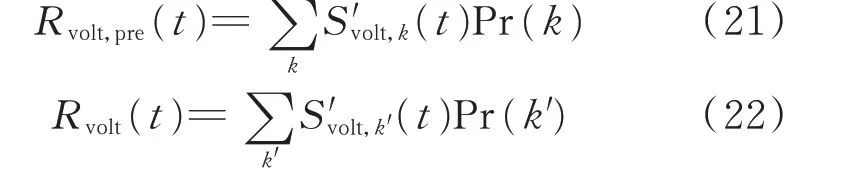
式中:S′volt，k′归一化后电压越限事件k′的严重度。

同理可以写出潮流风险约束Rflow(t)和变压器风险约束Rtran(t)如下。

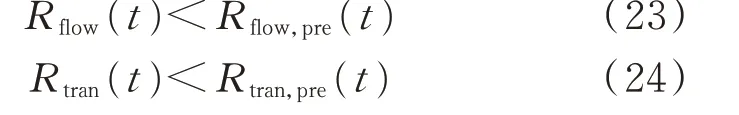
式中:Rflow，pre(t)和Rtran，pre(t)分别为预测潮流风险和预测变压器风险。

综上所述，优化调度模型的实质是以机组发电量及负荷调整量为决策变量的二次规划模型，通过基于LSTM-SVM 的概率预测模型得出下一时刻目标事件的发生概率，经由风险评估模型定量计算并判断该风险能否接受，并以此触发主动调控手段，合理避免电网运行过程中重大风险事故的出现。在计算用时方面，由于关键变量的时序预测模型及关键对象的概率预测模型均为离线构建，故模型在线计算的耗时主要集中于优化策略的制定部分。针对本文提前式的静态预防控制场景，利用模型预测所带来的缓冲处理时间（与预测时间尺度相同），优化程序可获得较长时间制定策略，因而在计算时间方面较为充裕，可满足在线主动控制的尺度要求。当系统规模扩大时，也可通过调节预测时间尺度进一步获取更长的处理时间。基于概率预测的电网主动调控策略的完整结构如图2 所示。

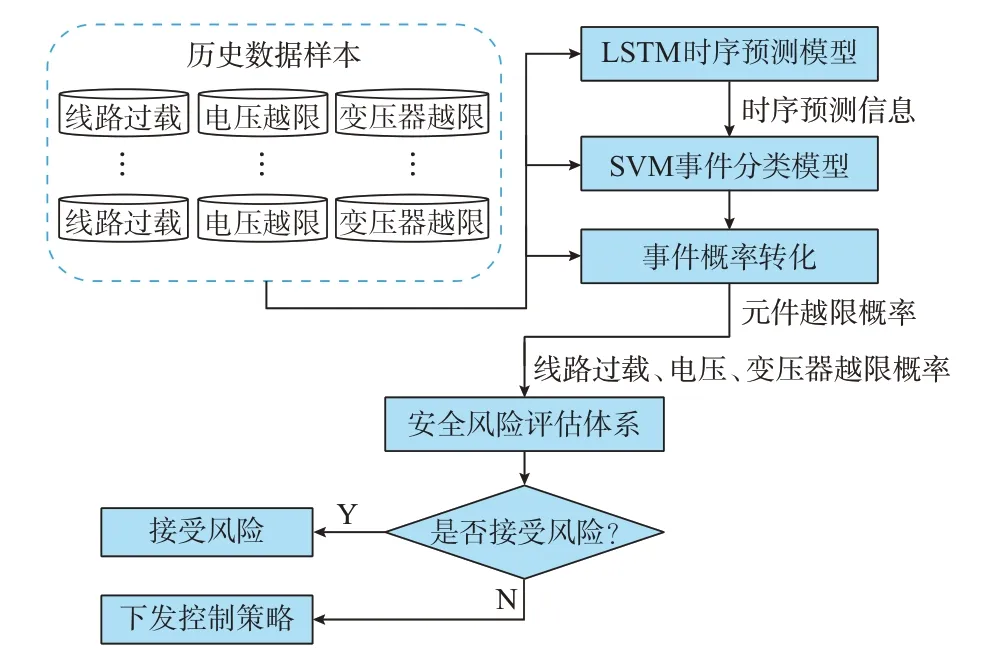
图2 基于概率预测的电网主动调控策略结构图Fig.2 Structure diagram of proactive regulation and control strategy for power grid based on probability prediction

3 算例分析

为验证所提方法的有效性，本文采用IEEE 39节点标准系统结合中国某省网负荷实际数据进行算例测试。

3.1 模型样本制作

本文采用的标准系统如附录A 图A1 所示，利用从中国某省网收集的实际负荷数据作为波动源，接入标准系统中，可产生线路潮流、节点电压和变压器负载波动数据，生成线路过载、电压越限、变压器过载等场景数据，从而得到时序预测模型及概率预测模型的训练及测试样本。本文选取时间跨度360 d、间隔5 min 的负荷数据，作为潮流断面样本生成的输入，共计生成103 678 个时间断面的潮流样本，该数据样本充分考虑了来自波动源的一年内的所有波动模式，包含单线路过载、多线路过载、单节点电压越限、多节点电压越限，以及上述过载事件并存的多重越限场景。基于潮流样本数据，计算得到系统历史严重度数值序列，并通过基于相关性分析的特征选择方法筛选了15 个关键变量，如附录A 表A1 所示。本文为这15 个关键变量构建了时序预测模型（共计13 个，包含2 个不需要预测的时间和季度特征）。与此同时，依据在历史上是否出现过越限事件，可筛选出部分关键线路、关键电压节点以及变压器支路，如附录A 表A2 所示，并为每一个对象构建一个概率预测模型（共计21 个），用于对未来时刻的系统安全风险进行评价。

3.2 时序预测模型构建

在时序预测模型构建过程中，选取70%的样本进行模型的构建和选择，剩余30%的样本作为时序预测模型的测试集。需要说明的是，时序预测模型在测试集上的输出叠加时间特性取值之后，将作为概率预测模型的测试输入，而其余30%样本（原测试数据集）将不会作为概率预测模型的测试数据，为了区分，先前预留的30%样本称为测试集，而利用时序预测模型得到的数据集为预测数据集，测试集可作为预测数据集的校验。预测数据集考虑了预测误差，将更加有效地评估概率预测模型的表现，关于预测数据集的描述详见附录B。

考虑到本文所提安全风险评估系统和实际生产调度相结合，采用过去8 个时间点的实际数据来预测未来1 个时间点。与此同时，利用交叉验证及网格搜索的方式每次将70%的样本进一步拆分为训练集和验证集，对每种参数组合对应的模型进行评估，从而获取最佳模型及参数设置。附录B 图B1 为最佳模型在训练过程中的损失迭代曲线，结果表明所构建的LSTM 预测模型在训练过程中损失函数值随着迭代次数的增加快速下降，且验证集误差始终略大于训练集误差，但差别不大，模型具有良好的泛化能力［37］。图3 为所筛选的13 个关键变量中部分变量的时序预测对比图。图3 中，时序预测曲线与实际曲线间的误差始终在较小范围内，可见各关键变量在未来的数值得到了良好的预测，这也为后续SVM 分类模型提供了精准的输入。

图3 LSTM 对于部分变量的预测表现Fig.3 Predicted performance of LSTM for some variables

在LSTM 模型构建完毕之后，将先前保留的30%样本输入，得到针对此30%样本的时序预测值，此数据集也是后续概率预测模型的输入数据，即预测数据集。

3.3 概率预测模型构建

在滚动预测模型的构建过程中，70%的样本用于模型训练，30%的样本用于模拟预测。于是，在分类模型的构建过程中，同样只能使用前70%的样本进行模型的择优和训练，在模型构建完毕后将使用上述预测数据集进行模型评价。本文采用交叉验证以及网格搜索的方式，每次将输入的70%样本进一步拆分，以保证预测结果的客观性。经过模型训练和择优，共计形成21 个概率预测器，从而完成了安全稳定风险评估体系的构建。

在进行模型择优时需要依靠一定的评价方式，对于二分类问题，常采用混淆矩阵来判断模型的好坏，并引申出查全率、查准率等评价准则［37］。正例通常代表非正常情况，而负例则代表正常情况，在电力系统中正例的样本数会远大于负例，属于不平衡分类问题，传统的依靠精度的方式已不再适用。进一步考虑不平衡的多分类问题，本文采用“宏”平均f1分数对分类模型进行评价，它将计算未加权的按类别f1分数，并对所有类别给出相同的权重。“宏”平均f1分数计算方式如下。

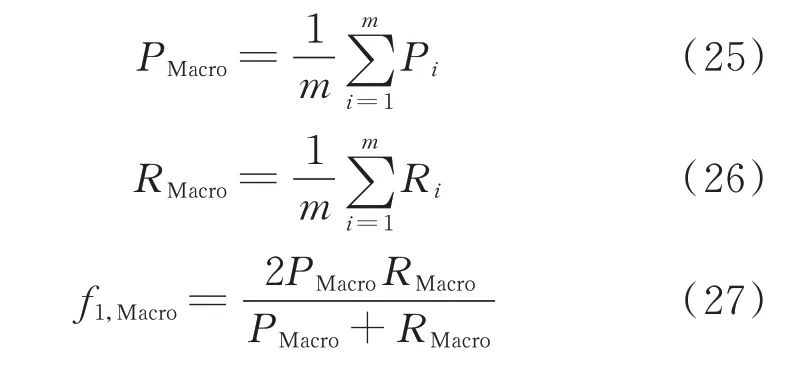
式中:f1,Macro为宏f1分数，能综合宏查准率PMacro和宏查全率RMacro来量度算法的性能；Pi为第i类样本的查准率；Ri为第i类样本的查全率；m为总分类数目。

基于“宏”平均f1分数可以筛选得到最佳模型及参数，从而完成关键元件的越限概率预测。本文将SVM 与部分常用算法进行了对比，以线路6 是否过载作为观测目标为例，图4 和图5 给出了各类算法在测试数据集以及预测数据集上的混淆矩阵图形，包括逻辑回归（logistic regression，LR）、随机森林（random forest，RF）、高斯朴素贝叶斯（Gaussian naive Bayes，GNB）以及SVM。

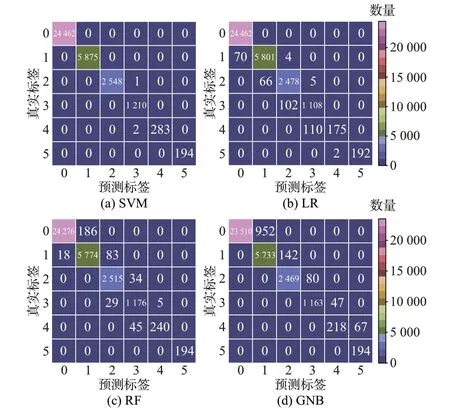
图4 各类分类器在测试数据集上的分类表现Fig.4 Classification performance of various classifiers on test data set

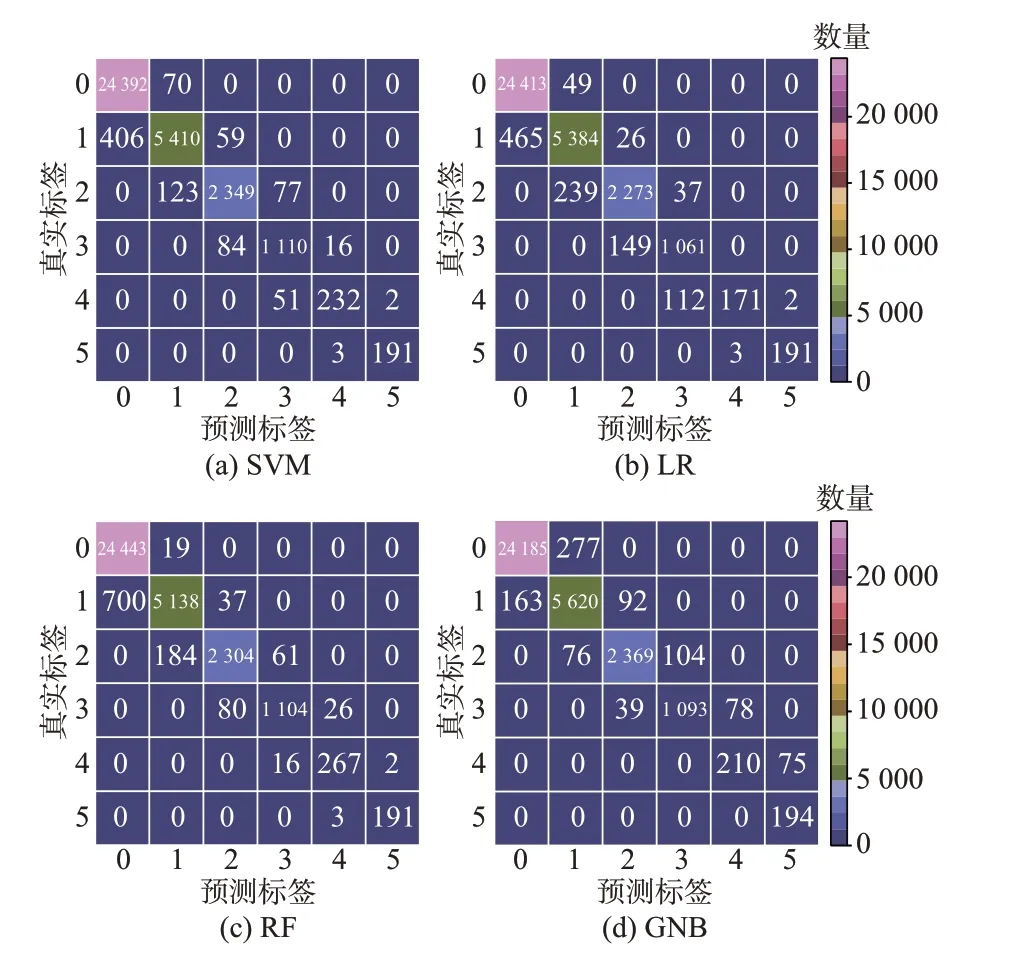
图5 各类分类器在预测数据集上的分类表现Fig.5 Classification performance of various classifiers on predictive data set

对比实验将线路6 的负载率划分为6 个区间，区间划分点依次为50%，60%，70%，80%，90%，其中小于50%和大于90%为开区间（为了留有一定的缓冲裕度，将上区间设置为大于90%），对线路6 负载的监测即可转化为六分类问题。从图4 和图5 可以直观看出，从测试集到预测数据集，每个模型的分类准确度均有不同程度的下降，这是因为预测误差的存在使得依靠原数据训练的模型精度受到了一定的影响，但两者精度效果差别不大也从侧面印证了时序预测模型的准确性。

对比不同模型在预测数据集的实际分类效果可以看出，SVM 虽在80%～90%的区间内要略逊色于RF，但在其他区间的表现均要优于其他分类器。在测试数据集中，SVM 除了在60%～70%区间内略逊色于GNB，其在剩余区间内均领先于其他分类器，可见SVM 的精度在此预测问题中总体上要优于其他常见分类器，这也是本文选择SVM 的要素之一。列出各模型在预测数据集以及测试数据集上的“宏”平均f1分数以及其他评价指标，如表1 和表2所示。

如表1 及表2 中所示，PMacro反映的是模型总体的查准率，表示模型将样本判断为正例的准确率；RMacro反映的是模型总体查全率，表示模型将正例样本准确找出的能力。实验结果表明，无论是在预测还是测试数据集中，SVM 的表现均优于其他模型，具有对越限情况良好的分类表现，可见本文所提出的概率预测模型可以实现对越限概率的有效评估。同时，本实验中利用网格搜索获取的最佳模型能够有效地对元件在未来的状态进行判断。

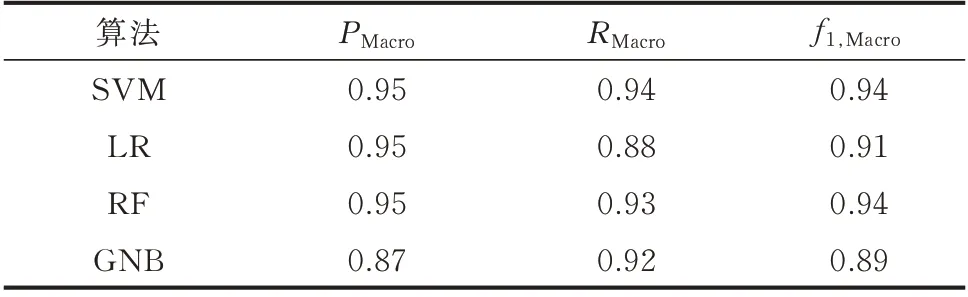
表1 各类分类器在预测数据集的表现统计Table 1 Performance statistics of various classifiers on predictive data set

表2 各类分类器在测试数据集的表现统计Table 2 Performance statistics of various classifiers on test data set

3.4 基于安全风险评估的主动调控仿真结果

在概率预测模型构建完成后，即可进行主动调控仿真验证。本实验设定严重度可接受阈值为0.095，即当预测出下一时间点全网风险大于0.095时，进入优化调度步骤，使用Yalmip 调用Cplex 求解器对上文所述优化模型进行求解得到调控指令。考察样本数据可发现，第696 个时间步全网风险之和超过设定阈值，故在第695 个时间步启动优化调度程序，对风险进行规避。选取第1 道调度指令下达的前后各12 个时间点绘制全网风险严重度图像进行比对，如图6 所示。

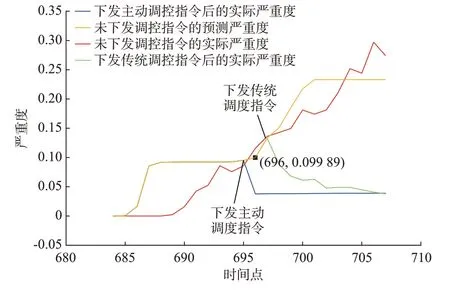
图6 考虑安全风险的主动调控前后系统严重度对比Fig.6 Comparison of system severity before and after proactive regulation considering safety risk

对比未下发调控指令时系统的预测严重度以及实际严重度评估结果可以看出，本文提出的基于概率预测的安全风险评估体系较好地实现了对系统安全风险的预测评估，成功对其走势进行了感知，有利于相关调度人员对系统未来总体安全态势的评估，并基于此做出准确判断。且从图6 可以看出，当安全风险评估模型对未来系统风险的预测值超过设定阈值之后，便启动了策略制定并实施主动调控，指令下发后全网风险量化值立刻降低，且始终维持在一个较低的水平（蓝色曲线），因此可以认为系统风险得到了控制。因此，本文所提出的模型可以有效地对系统风险进行预测并实施主动调控，对比传统调控方式（绿色曲线）可以提前将系统控制在安全状态，为系统争取了更多的缓冲时间。

为进一步验证模型的正确性和有效性，将主要线路在调度指令下发后的运行负载率与未进行调控的预测负载率进行比较。从图7 可以看到，当系统部分负荷持续增长，各关键线路及变压器负载均有不同程度的上升，而本文所提出的安全风险评估体系则会在线评估系统所面临的安全风险大小，并在超出设定阈值时启动调控策略的制定和指令下发，从而提前控制系统各关键线路及变压器的负载，避免越限，完成主动调控。从控制前后的各线路、变压器负载率数值可以看出，没有附加安全控制时总体负载持续走高，安全风险持续增大，并与图6 中系统总体安全风险预测走势（黄色曲线）相对应，此时系统真实安全风险走势也在上升（红色曲线），部分线路的负载率已超过90%，甚至接近100%，系统面临巨大安全风险，可见本文所提安全风险评估及预测方法实现了对系统真实情况的有效反映。采用基于风险评估的优化调度方法后，各关键元件的负载率均提前下降，并维持在允许范围内，可见系统的安全风险得到了有效控制。

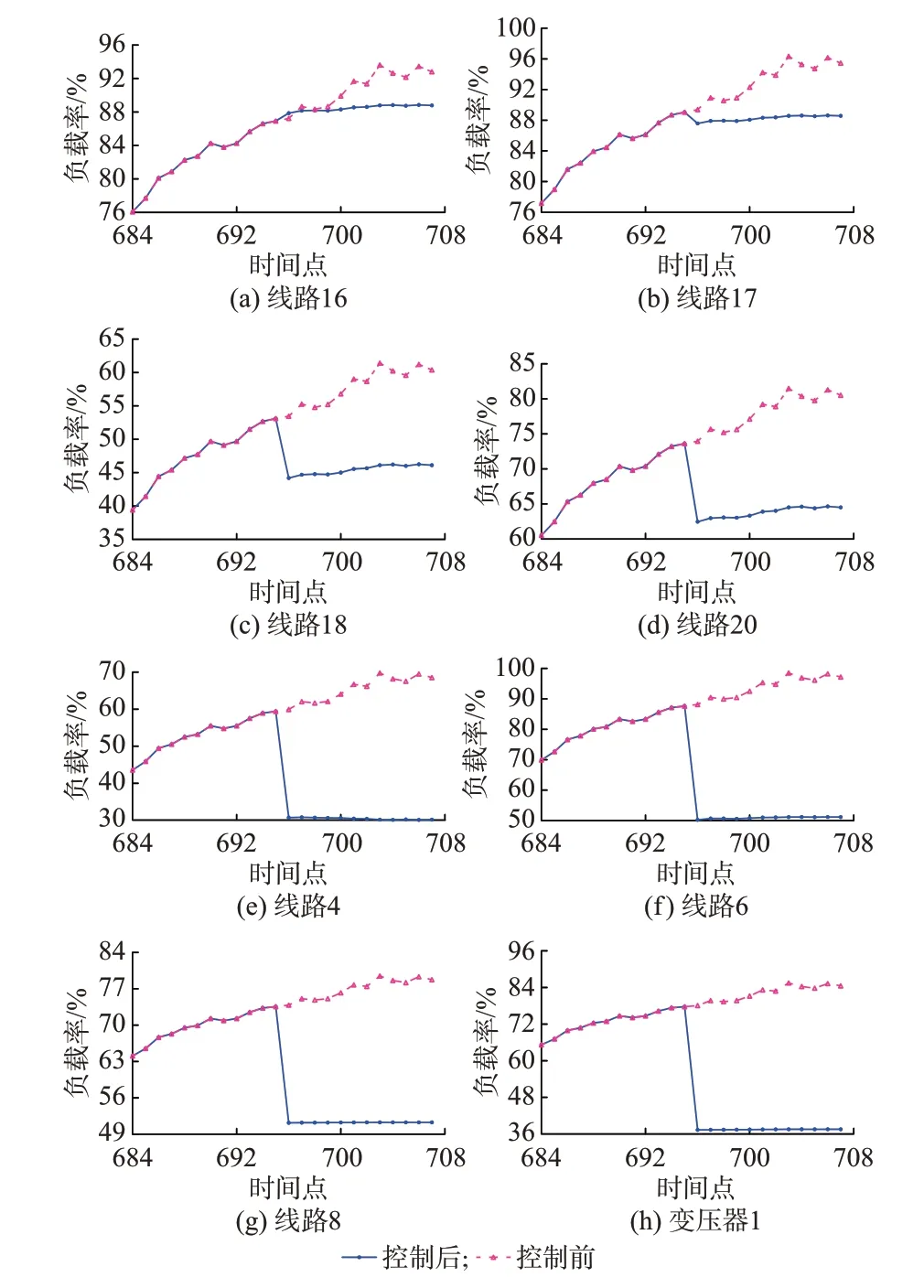
图7 主动调控前后各关键线路及变压器负载率对比曲线Fig.7 Load ratio comparison of critical lines and transformers before and after proactive regulation and control

核算本文所提主动调控策略在该算例中的调控成本，与传统被动调控方式对比，如表3 所示。传统方式的调控成本为39 087.42 元，而主动调控成本为32 057.57 元，仅为传统调控方式的82.02%，可见本文所提主动调控策略不但有效预测并降低了系统安全风险，在调控经济性方面也优于传统控制方式；对比调控指令下发时间点，主动调控能够做到提前事件5 min，相比传统调控方式滞后5 min 而言能够起到更好的预防作用；对比调控指令下发后5 个时间点内的平均系统严重度，主动调控后系统平均严重度仅为传统调控方式的57.99%。综上所述，本文所提出的基于概率预测的主动调控方式在调控成本、动作时间、控制效果等方面均优于传统调控方式，可以有效预测并降低系统安全风险，以更低的调控成本完成预防控制，提高系统的安全裕度。