基于深度神经网络的数据驱动潮流计算异常误差改进策略

雷江龙，余 娟，向明旭，杨知方，杨 燕，李文沅

（输配电装备及系统安全与新技术国家重点实验室（重庆大学），重庆市 400044）

0 引言

潮流计算作为电力系统分析的必要工具，广泛应用于运行优化、安全分析等场景，其计算效率及精度影响着电力系统安全稳定运行［1］。近年来，为应对风能、光能等新能源大规模并网所带来的强不确定性，N-1 安全校核［2］、概率潮流计算［3］和实时安全分析［4-5］等需要进行大规模重复潮流计算的场合将面临更高的计算效率和精度要求。非线性交流潮流模型的求解方法计算精度高，但面对大规模重复潮流求解的计算需求时，计算效率面临挑战［6］。线性化潮流模型可有效提高计算效率且不存在收敛问题，但线性简化潮流模型牺牲了计算精度［7-9］。

随着数据驱动技术的不断发展，已有研究提出采用神经网络（neural network，NN）提高大规模重复潮流计算的求解效率。NN 通过对潮流数据特征的迭代学习，实现大量系统状态至对应潮流结果的直接映射，计算效率高且不存在收敛问题，具体包括极限学习机［10］、反向传播神经网络［11］、径向基函数神经网络［12］、深度神经网络（deep neural network，DNN）［13-15］等。相较于浅层NN，DNN 具有更强的特征提取和泛化能力［13］，在电力系统研究中已受到广泛关注。然而，现有DNN 训练方法存在误差异常问题:即使模型整体精度已达标，但仍有部分潮流变量的误差较大［13-15］。上述问题将影响N-1 安全校核等场景下潮流越限判别的准确率，威胁电网安全稳定运行。而如何处理数据驱动潮流分析方法的异常误差问题现有文献鲜有涉及，还有待进一步研究。

对此，本文结合DNN 参数更新过程及数据标准化原理，对数据驱动潮流分析误差异常的成因进行了理论分析。为改善该问题，本文在现有DNN训练框架的基础上，面向潮流计算提出了一种基于动态学习权重的DNN 自适应训练方法，可引导DNN 高精度学习误差异常的潮流变量，提升潮流计算精度。本文主要贡献如下。

1）根据DNN 梯度更新理论及数据标准化原理，理论分析部分潮流变量存在异常误差的原因。本文发现DNN 训练需依据的标准化误差，无法准确反映各潮流变量的真实学习误差和实际精度需求是导致潮流计算存在异常误差的重要原因之一。

2）提出基于动态学习权重的DNN 自适应训练方法。通过每轮迭代验证集的真实学习误差、越限误判率及误差评价标准，动态设置各潮流变量的学习权重，有效衡量训练中各潮流变量的真实学习效果，并嵌入DNN 引导各潮流变量的学习。

1 基于DNN 的潮流计算模型

本文所构建的DNN 潮流训练模型将考虑负荷、新能源出力不确定性以及支路或发电机故障引起的N-1 拓扑结构变化，但并未关注网架新增线路情况。若网架新增线路，需针对新场景重新训练DNN 潮流模型，此时可基于迁移学习技术［16］进行快速训练。DNN 输入特征向量Xf包括节点注入功率和拓扑结构变化信息（其中，拓扑结构信息表征方法详见文献［15］）。输出特征向量Yf包括节点电压幅值、电压相角、支路有功和无功功率。

DNN 基本训练流程如图1 所示。为消除不同类型潮流变量间（如电压幅值、相角、支路功率等）的量纲差别，保证DNN 训练的收敛性，在对DNN 进行训练前，需对样本数据（包括输入和输出）进行标准化预处理［17-18］。本文潮流数据中包含源荷及拓扑变化，宜采用z-score 标准化方法［15］。以输出数据为例，z-score 标准化方法如式（1）所示。

图1 DNN 基本训练流程Fig.1 Basic training process of DNN

式中:Yf，mn为第m个样本中第n个潮流变量的待标准化数据；Ymn为第m个样本中第n个潮流变量的标准化结果；μY，n为第n个输出潮流变量的均值；δY，n为第n个输出潮流变量的标准差。

DNN 主要包括单个输入层、多个隐藏层和单个输出层，各层由若干神经元构成，仅层与层之间的神经元相互连接。多隐藏层的结构使得DNN 相较于浅层网络具有更强的特征提取能力，适用于拟合具有强非线性的潮流方程。DNN 模型由输入计算得到输出的前向传播过程如式（2）—式（3）所示。

式中:X为标准化的DNN 输入；为标准化的DNN预测输出；L为DNN 的总层数；Xl为第l（2 ≤l≤L）层的输入；为第l层的预测输出；fl(·)为第l层的预测输出函数；s(·)为神经元的激活函数，本文分别选择ReLU 函数和线性函数作为隐藏层和输出层的激活函数；Wl-1为第l-1 层与第l层之间的权重；bl为第l层的偏置。

训练后的DNN 可根据潮流输入直接映射得到潮流计算结果。为得到实际潮流计算结果还需对DNN 预测输出进行反标准化处理，如式（4）所示。

最后，通过统计计算结果来评价模型性能。

2 异常误差问题描述及原因分析

本章将对现有数据驱动潮流计算方法面临的异常误差问题进行详细描述并分析其产生的原因。

2.1 问题描述

电力系统潮流计算不仅需要关注DNN 整体精度，同时还要求各节点、支路的潮流变量具有较高的学习精度。因此，对比分析了各潮流变量的学习精度，发现现有DNN 潮流计算模型存在如下问题:即使DNN 整体精度已满足要求，但仍有部分潮流变量存在异常误差。基于现有训练方法［15］的DNN 模型测试误差如表1 所示；电压幅值和支路有功功率的统计误差如图2 所示。由表1 可知，DNN 模型的整体精度较高，但不同类型潮流变量的学习精度存在较大差异。其中，电压幅值和支路有功功率的误差明显大于电压相角和支路无功功率。此外，尽管电压幅值和支路有功功率的整体精度较高，但如图2 所示，部分潮流变量误差存在异常。例如，支路27的有功功率统计误差高达20.90%，且经测试证明，支路27 处的异常误差将最终影响N-1 安全校核的准确率。

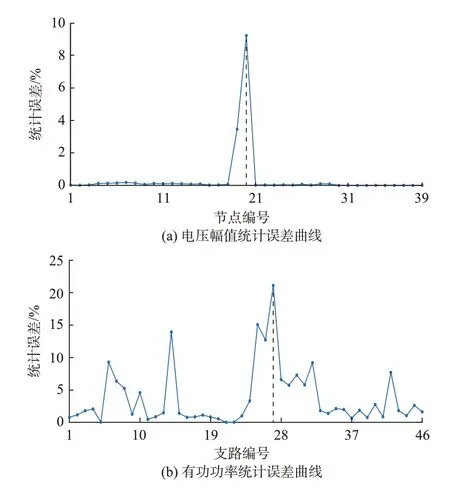
图2 潮流变量统计误差曲线Fig.2 Statistical error curves of power flow variables

表1 IEEE 39 节点系统的DNN 模型误差Table 1 DNN model error of IEEE 39-bus system

2.2 引起DNN 潮流模型异常误差的原因分析

本节将对引起DNN 潮流模型异常误差的原因进行分析。DNN 训练的数学过程是:通过不断迭代训练来优化模型参数ρ，从而降低DNN 预测值Y^mn与样本真实值Ymn之间的偏差。该偏差的大小通常通过损失函数表征。本文选择均方差函数作为损失函数，其计算公式如式（5）所示。

式中:M为训练样本数量；N为输出潮流变量的维数；J为损失函数；Y为标准化DNN 的预测输入。

式（5）所示损失函数中的误差项为标准化后的误差，而在评价DNN 预测精度及应用DNN 进行潮流计算时，所关注的则是各潮流变量的真实误差，即反标准化后的误差。本文以z-score 标准化方法为例进行分析，由式（1）的标准化公式，可将损失函数变换为以真实误差表示，如式（6）所示。

由式（5）和式（6）可知，标准化前后的训练误差通过各潮流变量的标准差相互关联。但由于各潮流变量的标准差大小存在差异，各潮流变量误差在标准化前后的相对大小并不一致，将导致DNN 在训练过程中无法准确获悉潮流变量的真实误差，影响DNN 对各潮流变量的学习效果。下面将进行详细阐述。

DNN 通过反向传播过程更新参数，本文采用RMSProp 算法训练DNN［19］，并据此说明异常误差产生的原因，DNN 模型参数的更新过程具体如下。

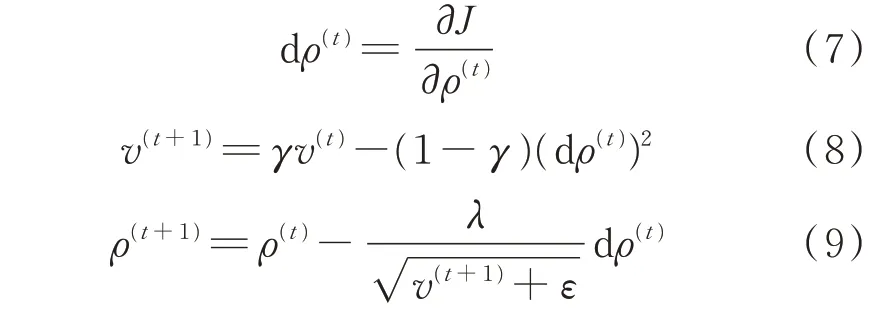
式中:ρ(t)为第t+1 轮迭代时待更新的模型参数；ρ(t+1)为更新后的模型参数；dρ(t)为第t轮迭代时模型参数的梯度；v(t+1)为第t+1 轮迭代时的累积动量；γ为动量衰减率；λ为学习率；ε为取值非常小的常数。

由式（7）—式（9）可知，DNN 参数梯度的大小和方向将直接影响DNN 参数更新量，进而决定着DNN 对各潮流变量学习效果的差异性。同时由式（8）和式（9）可知，当前迭代计算得到的梯度还会通过累积动量影响后续的迭代更新过程。本文所选激活函数为ReLU 和线性激活函数，对于某一次迭代而言，其模型任意一层参数的梯度计算如式（10）—式（13）所示。

由式（10）—式（13）可知，DNN 参数梯度将由式（10）和式（11）所示DNN 各层输出的梯度决定，其与标准化训练误差-Yl，i和真实训练误差-Yfl，i均呈正相关，与潮流变量的标准差δY，i呈负相关。因此，当标准差δY，i较大时，潮流变量真实训练误差对梯度的影响将较小。相反，对于标准差δY，i较小的潮流变量，其真实训练误差对梯度的影响将更为显著。

综上所述，DNN 在训练过程中无法计及真实学习误差以及精度需求，导致其无法获悉各潮流变量的真实学习效果，使得训练中所重视的潮流变量（标准化误差较大的潮流变量）可能的实际学习效果较好，反而忽视实际学习效果较差的潮流变量，最终影响DNN 对各潮流变量的学习效果。由于各标准化方法处理数据思路类似，都需选择基准值缩放数据，故选择其他标准化方法也将存在上述问题。

3 基于动态学习权重的DNN 自适应训练方法

本文在现有DNN 训练框架中引入潮流变量动态学习权重，从而合理引导DNN 模型参数的更新过程，改善部分潮流变量误差异常的问题。

3.1 内嵌学习权重的DNN 自适应训练框架

本文通过在损失函数中嵌入各潮流变量的学习权重指导DNN 训练过程。在嵌入学习权重后，损失函数由式（5）变为式（14）:

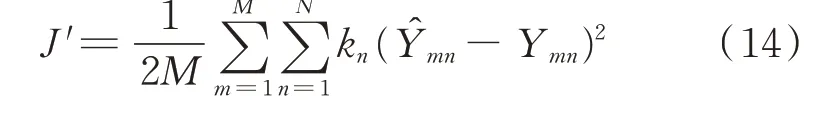
式中:J′为更新后的损失函数；kn为第n个潮流变量的学习权重。

嵌入的学习权重将作用于DNN 模型参数的更新过程，指导DNN 的训练，梯度计算过程中的式（10）将变为式（15）:

由式（15）及式（8）和式（9）可以看出，所嵌入的学习权重能通过损失函数直接影响模型参数的更新过程。学习权重较大的潮流变量对模型参数更新的影响程度将变大；对于权重很小或者为零的潮流变量，其对参数更新的影响程度将随之减小。学习权重将指导DNN 对误差异常潮流变量的学习，从而取得更好的训练效果。而其中的关键在于如何设置学习权重，使其能有效反映DNN 训练过程中各潮流变量的真实学习效果。

3.2 学习权重动态设置方法

如2.2 节所述，各潮流变量标准差的不同是引起本文所述问题的主要原因。因此，较为直观的权重设置方法是根据各潮流变量的标准差设置学习权重。但由于各潮流变量的标准差是固定的，而在训练中各潮流变量学习误差的相对大小关系是变化的，仅使用标准差将无法动态追踪潮流变量的学习误差变化情况，存在一定局限性。对此，本文基于验证集学习情况，提出了一种学习权重动态设置方法，具体介绍如下。

由于不同类型潮流变量的真实误差在量纲上存在较大差异，故本文需针对不同潮流变量类型分别设置学习权重。验证集不同于训练集，可反映DNN对未知样本的学习效果。为避免模型出现过拟合，本文通过验证集的真实学习误差来表征每轮迭代DNN 模型对各潮流变量的真实学习效果，并据此为各潮流变量动态设置误差相关学习权重。此外，早停法［20］的应用可进一步防止过拟合现象。以电压幅值为例，由验证集误差确定各节点电压幅值的误差相关学习权重的具体过程见式（16）和式（17）。

潮流变量整体误差较小不一定代表其越限误判率较小。所以，在N-1 安全校核等需要考虑越限判别情况的场景下，DNN 除绝对学习误差外，还需关注越限判别准确率。因此，本文进一步根据验证集中各潮流变量的越限误判情况为其设置越限相关学习权重，使得训练过程关注误判严重的潮流变量，如式（18）所示。

将误差相关学习权重和越限相关学习权重进行组合，构成最终学习权重，如式（19）和式（20）所示。

前述针对不同类型潮流变量分别设置了相应的学习权重。然而，现有DNN 训练方法还存在某些类型潮流变量的整体误差统计指标偏大的问题。对此，本文进一步提出基于学习权重调整系数的误差均衡策略。其主要思想是通过给不同类型潮流变量的学习权重增加合适的调整系数，从而以适当牺牲误差较小潮流变量类型的学习精度为代价，提升误差较大潮流变量类型的学习精度。添加调整系数后的学习权重的表达式如式（21）所示。

式中:βV、βθ、βP、βQ分别为电压幅值、电压相角、支路有功和无功功率的权重调整系数；分别为对应的组合学习权重。调整系数根据每轮迭代中各潮流变量的误差评价指标进行确定。

3.3 内嵌学习权重的DNN 模型训练流程

本文所提基于动态学习权重的DNN 自适应训练流程如图3 所示。

图3 内嵌学习权重的DNN 自适应训练流程Fig.3 DNN adaptive training process with embedded learning weights

4 算例分析

本文在IEEE 39、IEEE 118 和Polish 2383 节点系统上仿真验证所提方法的有效性。

4.1 算例说明

本文在IEEE 39 节点系统的节点23、24 及25 上分别接入容量为260 MW 的风电场，在节点17、18及19 上分别接入容量为200 MW 的光伏发电站，新能源渗透率为20%。对于IEEE 118 节点系统，容量为330 MW 的风电场和容量为250 MW 的光伏发电站分别接到10 个不同的节点上，新能源渗透率达30%。风速和太阳辐射强度的分布、参数及风光转换模型参见文献［21-22］。假定负荷波动服从正态分布，其均值参考IEEE 标准算例，标准差为均值的10%。本文所用潮流训练样本考虑N-1 支路故障及N-1 发电机组故障［22］。

本文将在不同算例中对比如下方法，以验证本文所提方法的有效性。

M0:基于牛顿-拉夫逊算法的交流潮流计算，结果作为参考值。

M1:基于DNN 的潮流计算，采用常规DNN 训练方法［14］。

M2:在M1 基础上，按潮流变量类型将标准差归一化至［0，1］，并将其设为学习权重。

M3:在M1 基础上，引入本文所提的误差相关学习权重。

M4:在M3 基础上，进一步引入本文所提的越限相关学习权重及调整系数。

M5:在M1 基础上，按不同潮流变量类型进行标准化预处理，标准差选为同类型潮流变量标准差的均值。

M6:直流潮流模型。

为避免超参数不同带来的影响，在进行对比时，不同方法均采用相同的超参数设置。对于IEEE 39节点系统，DNN 模型共有4 层隐藏层，每层有350 个神经元；对于IEEE 118 节点系统，DNN 模型共有4 层隐藏层，每层有500 个神经元。各算例训练集样本数均为80 000，验证集和测试集样本数量均为10 000，迭代次数为1 000；初始学习率设置为0.001，每轮迭代以95%衰减直至0.000 01。

本文使用如下指标来对比不同方法的训练精度。电压幅值、电压相角、支路有功和无功功率的绝对误差超过阈值的比例分别表示为PV、Pθ、PP和PQ，其具体设置见表1。本文算例均在AMD Ryzen 5 3600X 3.8 GHz 6 核CPU，32 GB RAM 硬件环境下完成。

4.2 算例验证及分析

4.2.1 不同潮流变量学习精度对比

本节将验证所提训练方法在改善部分潮流变量存在异常误差问题方面的有效性。不同方法下各潮流变量的最大统计误差如表2 所示。由表2 可见，方法M1 中电压幅值和支路有功功率的最大统计误差存在异常，难以满足计算需求。而所提方法M3、M4 可显著提升各潮流变量中的最大统计误差。相较于M3，M4 通过误差均衡策略，以略微牺牲原本误差较小潮流变量（电压相角和支路无功功率）的学习精度为代价，进一步降低了电压幅值和支路有功功率的最大统计误差。而M2、M5 在支路有功功率上各潮流变量的最大统计误差存在明显的激增。

表2 不同方法下各变量最大统计误差Table 2 Maximum statistical error of variables with different methods

为进一步说明所提方法的有效性，图4 展示了方法M1 至M5 在测试集上电压幅值和支路有功功率的统计误差。由图4 可知，M3、M4 相较于M1 在误差异常潮流变量处的精度均存在不同程度提升。其中，支路27 有功功率的统计误差由20.90%（M1）分别降低至6.81%（M3）和1.27%（M4）。M2、M5 相较于M1 而言，其在绝大部分潮流变量上的精度都有不同程度下降，甚至在支路有功功率上产生了新的异常误差，其中M2 的最大统计误差高达94.93%。

图4 不同方法在电压幅值和支路有功功率上的统计误差Fig.4 Statistical error of different methods on voltage amplitude and active power of branch

经由分析发现，M5 对同一类型潮流变量选取相同的标准差，虽然可保证标准化前后各潮流变量的误差相对大小关系不变，但其也使得标准差更大的潮流变量在标准化后数值相对更大，而标准差更大并不能代表其真实学习误差越大。因此，M5 等价于以标准差的相对大小引导DNN 学习，其结果同M2 相似，均无法保证DNN 的训练效果。

4.2.2 DNN 模型整体性能对比

本节将进一步验证所提方法在提升DNN 模型整体性能方面的有效性。不同方法下的DNN 模型整体测试误差如表3 所示。由表3 可知，相较于M1而言，所提方法M3、M4 可有效提升各类型潮流变量的学习精度。其中，IEEE 39 节点系统中支路有功功率的误差评价指标由3.69%（M1）分别降低至1.97%（M3）和1.42%（M4）。而M2、M5 在部分潮流变量整体精度上相较于M1 也存在明显下降。

不同方法训练集电压幅值和支路有功功率的均方误差曲线见图5。其中，为使损失函数的变化情况更易观测，对曲线进行了截断。由图5 可见，方法M2 由于无法准确追踪各潮流变量误差的相对变化情况，相较于M1 在误差下降速度和最终均方误差值上未有优势，且在部分算例中还出现训练误差上升的情况，由于早停法作用提前终止了训练（如图5（b）所示）；M3、M4 相较M1 而言具有更快的误差下降速度，且在训练终止时，具有更低的均方误差值。

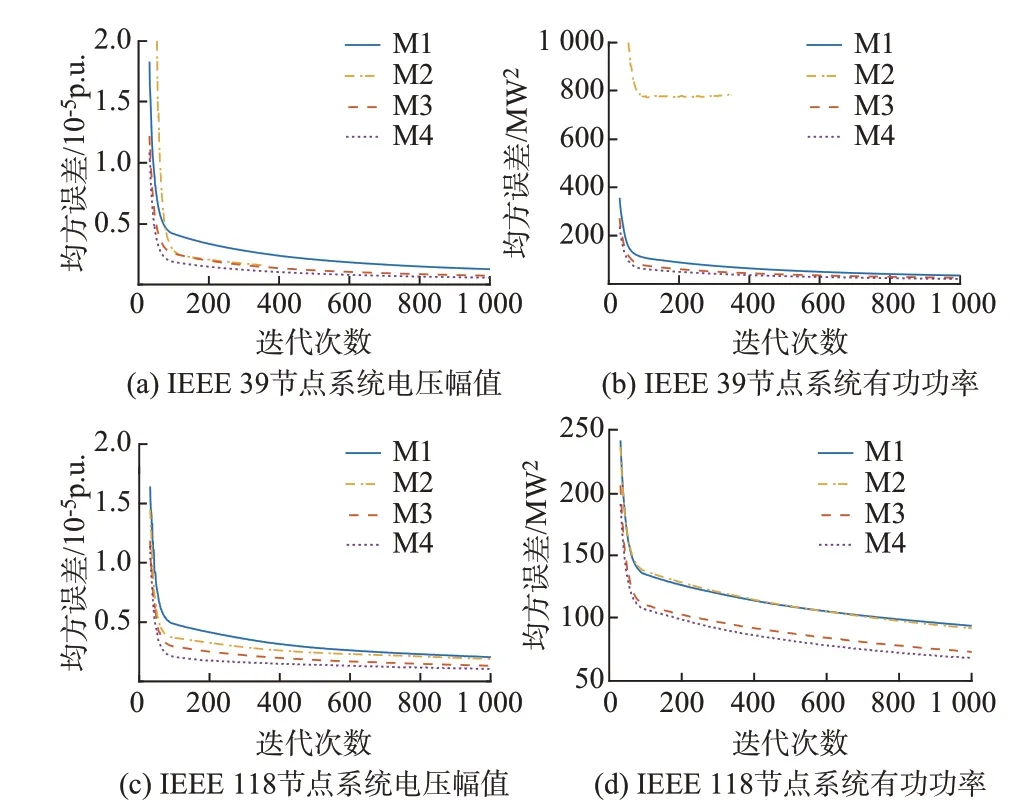
图5 均方误差曲线Fig.5 Curves of mean squared error

综上所述，本文所提方法不仅能够提升DNN模型整体性能，更重要的是还能够有效改善误差异常变量的精度。

4.2.3 所提方法的适用性验证

为验证所提方法在大规模系统的适用性，本节在Polish 2383 节点系统的实际算例中进行了仿真测试。本算例考虑N-1 支路故障，DNN 模型共包含3 个隐藏层，每层有1 500 个神经元，不同方法下各潮流变量最大统计误差及DNN 模型误差分别如表2 和表3 所示，其中上节仿真已验证M2、M5 的局限性，此处不再比较。仿真表明本文所提方法在实际规模的测试系统中具有较好适用性。

表3 不同方法下DNN 模型误差Table 3 Error of DNN with different methods

为验证超参数寻优对异常误差及所提方法有效性的影响，本算例将贝叶斯优化方法［23］搜索最佳超参数后训练所得模型与经验设置训练所得模型进行对比测试。图6 展示了测试集上支路有功功率的统计误差。由图6 可知，通过合理的超参数设置能够提升训练效果，但其最大统计误差仍较高。而本文所提方法在不同超参数下都可降低潮流变量的最大统计误差，有效改善了误差异常的问题。

图6 支路有功功率统计误差Fig.6 Statistical error of active power of branches

4.2.4 考虑不确定性的N-1 安全校核性能对比

本节将验证所提方法在工业界的实用价值。为应对日益增长的不确定性对电力系统运行的影响，电力系统N-1 安全校核除了考虑线路故障场景外，还需要考虑新能源出力等不确定性的影响，将导致安全校核的计算量激增［24］。本节将以Polish 2383 节点系统为例，验证所提方法在N-1 安全校核场景中的有效性。本算例考虑8 个风电场、光伏电站等新能源场站，每个场站考虑2 个不确定性场景，则需计算741 376 个待校核样本。表4 展示了不同方法下支路有功功率安全校核误差及计算时间。

如表4 所示，M0、M6 均需依次计算所有待校核样本，其计算时间达小时级。相比之下，基于DNN潮流模型的M1、M3、M4 在安全校核计算速度上存在大幅提升，且具有较高安全校核精度。本文所提方法M3、M4 相较于M1 可有效改善潮流变量误差异常的情况，从而可进一步提升校核精度。由于DNN 模型仍存在计算误差，故其不可避免存在较小的误差，但通过采用松弛越限阈值筛选出更多样本的方法［25］，可进一步提升校核精度。

表4 安全校核误差及计算时间Table 4 Safety check error and calculation time

5 结语

近年来，基于DNN 的数据驱动潮流计算方法得到广泛关注。然而，在现有DNN 训练方法下，即使模型整体精度已达标，但仍有部分潮流变量存在异常误差。对此，本文基于DNN 梯度更新理论及数据标准化原理，对上述问题的成因进行了理论推导分析。为改善该问题，本文面向潮流计算进一步提出了基于动态学习权重的DNN 自适应训练方法。该方法通过在DNN 训练过程中嵌入可反映潮流变量真实学习效果的学习权重，指导DNN 重点学习误差异常的潮流变量。仿真结果表明，所提方法可有效提升误差异常潮流变量的学习精度以及DNN 模型的整体性能，并有助于提升潮流越限判别精度及计算时间。为实现快速准确的大规模潮流重复求解提供了技术支撑。

本文所做的异常误差原因分析关注于数据处理对训练过程造成的影响，而数据特性及模型结构差异等其他因素的影响机理还有待进一步研究。