离岸流灾害水动力学过程的数值模拟研究

2022-01-11田海平陈雷王维辛立彪

海洋学报 2021年12期

田海平，陈雷,2*，王维，辛立彪

( 1. 太原理工大学力学国家级实验教学示范中心，山西太原 030024；2. 西北工业大学力学与土木建筑学院，陕西西安710129)

1 引言

离岸流是一股垂直于海岸，冲向深海的强劲水流[1]，其宽度一般小于10 m，长度在几十到几百米不等，流速一般在0.3～2 m/s，有时可高达3 m/s[2-3]。流体在受到风力、引力、地形变化等各种因素作用下做周期性振动，并且朝着固定的方向传播，进而形成波浪。当波浪传播到近岸区的时候，其运动状态会发生复杂的变化，如折射、反射、绕射及破碎等，形成沿岸流和离岸流等近岸流。这些近岸流会影响近岸区的泥沙和污染物等物质的输送，从而改变海滩环境和近岸区的地形[4]。

离岸流类型不同，形成因素也因海滩环境和近岸地形的差异而不同[5]。其中，最典型的沟槽离岸流[6]就是水流冲破水下沙坝的阻挡而形成的。沙坝和沙滩共同组成了一个类似“堰塞湖”的水池地貌。波浪朝着海岸运动时，会提供足够多的动力将海水推到水池当中，水池中的水会逐渐堆积，最终大量的海水会在沙坝的某些薄弱部位突破，从而形成强劲的离岸流。通常认为这种离岸流由流根、流颈和流头3部分组成[7]，其结构如图1所示。

图1 离岸流结构示意图Fig. 1 Schematic diagram of rip currents

目前我国对于离岸流的研究工作正处于起步阶段，对不同非线性波产生离岸流的数值模拟工作较少，也尚未形成一套完整的离岸流预警系统。对离岸流的水动力学过程的认识存在不足，规律性和定量化结果仍比较缺乏。本文基于二阶Stokes波浪理论，采用不规则的沙坝模型对典型的沟槽离岸流进行了三维数值模拟，分析了不同流层离岸流的强度和三维速度场的分布特征，对离岸流水动力过程进行了细致的讨论，也探讨了入射波波高对离岸流强度的影响，对深入认识离岸流、防范离岸流危害具有积极意义。

2 数学模型

2.1 控制方程

本文以常黏度的不可压缩黏性流体为研究对象，所使用的坐标系是欧拉描述中的直角坐标系。u、v、w是流体t时刻在点（x，y，z）的速度的分量；fx，fy，fz为单位体积流体受到的外力；常数ν 为运动学黏性系数；ρ 为流体密度；p为压强。

连续性方程为

N-S方程本质为牛顿第二定律：

医学英语作为一种重要的科技文体，句子中派生词多，名词化结构多，被动句多，非谓语动词，长难句较多。在医学英语翻译中，英语语法中的复合句（包括有名词性从句，定于从句和状语从句）都属于复杂的句子，也称之为长难句。在翻译这些复杂句时，需要做到从句法角度准确分析主句以及各个从句，采用归化的方法，做到原文和译文句法对等。笔者将依托尤金奈达的功能对等理论，从医学英语的翻译实例来进行论述，通过对比中英两种语言的句法的差异性，通过三种传统的翻译方法：顺译法，逆译法与重组法来进行分析，力求让学生领悟到如何在译文中做到与原文的句法对等。

2.2 二阶Stokes波浪理论

本文基于二阶Stokes波浪理论对离岸流开展数值模拟。Stokes波浪理论是Stokes在1847年提出来的，假定波浪运动也是势运动，认为水波的运动是不可压缩理想流体在重力作用下的无旋运动。当波陡ς较小时，波动问题是一个弱非线性问题，采用摄动法求解，假设速度势函数 ϕ和波面函数 η 是波陡 ς这个微元参数的幂级数

通过有限振幅波浪理论中Stokes波浪理论的二阶近似解，即n=2时，求出速度势函数和波面函数的解。

速度势函数为

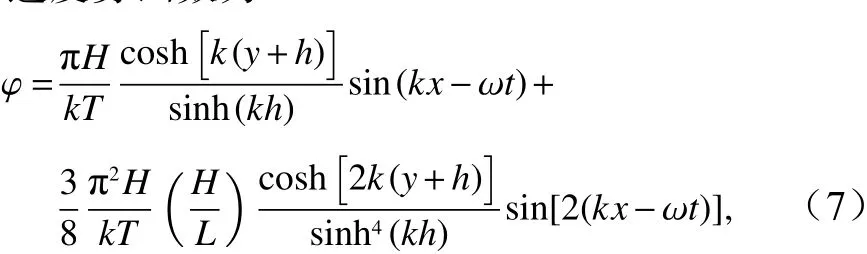
将速度势函数分别对x和y求偏导，水质点流速场如下

波面函数为

二阶stokes波的水质点运动轨迹不再为封闭的椭圆轨迹线运动，波浪传播方向有位移，称为“质量迁移”，（x0,y0）为初始的水质点初始位置，迁移后的位置（X,Y）为

1个周期的质量迁移为

式中，H为波高；k为波数；T为波浪周期；L为波长；h为静水深度；波陡 ς =H/L；ω为圆频率； s inh、cosh 分别为双曲正弦函数和双曲余弦函数。

2.3 自由表面跟踪方法

为了将液相和气相区分开，采用流体体积法（Volume of Fluid, VOF）方法[17]捕捉自由液面。该方法具体的数学理论是定义一个流体体积函数Fq,Fq表示在计算域内的每个单元的第q相流体所占的体积与该单元的体积之比。若Fq=1，则表示该单元被第q相流体占满；若Fq=0，则表示该单元没有第q相流体；若Fq在0～1之间，这种单元体称作交界面单元体。在每一个单元体内，两相流体的体积分数为1，即

又因为Fq(x,y,z,t)=0，满足输运方程

求解式（16）即可得到计算域内每个单元体液相所占的体积分数的百分比，从而确定自由液面的位置。

3 三维波浪数值模型

采用数值模拟可以较为系统地研究离岸流运动状况，目前使用的数值模型分为两类：时均模型和时域模型[16]。波浪时均模型求解思路是将流体的运动方程在一个周期上进行平均，通过求解时均方程得到流场，以辐射应力来考虑波浪的作用。这类模型计算时间短，对电脑硬件要求低，但是不能考虑到波流耦合作用产生的非线性影响。另一种就是波浪时域模型，此模型直接对波浪运动的过程进行求解，计算速度相对较慢。

Haller 等[18]进行了带沟槽沙坝的实验研究，本文数值模拟采用的模型在此基础上进行了一些优化，是为了使沙坝更接近自然水流冲击形成的情况。本文未采用传统的等截面积沙坝，而是将沙坝整体倾斜了3.83°，形成了中间窄两边宽的条状沙坝。模型忽略了自然沙坝的不对称性[19]，采用理想化的单沟槽对称斜坡模型，如图2所示。同时忽略沙床底部粗糙度影响，简化为平整固体壁面。模型计算尺寸为25.17 m×15.80 m×3.39 m，沙滩的倾角为7.09°，其中两段沙坝各长为7.17 m，沟槽宽度为1.46 m，水平坝面和倾斜坝面之间设置了半径为8 m的倒角，以便光滑过渡。

图2 可产生离岸流的典型海滩计算模型Fig. 2 Typical beach calculation model which can produce rip current

数值模拟中，液相为水（不可压缩，黏度为0.001 003 kg/(m·s)），气相为空气，气液界面表面张力为0.07 N/m。初始流场域静止。计算采用SST k-ω湍流模型。初始静水深度h为1.50 m，即图2a 中，Y=0～1.5 m的流体区域，F的初始值为1；其余的区域（气相）初始值为0。自由液面通过VOF来确定液相所占的体积。

计算域中每个面的编号设置如图2a所示，其边界条件分别设置如下：（1）入口处设置为速度入口边界，波高H初始条件分别为0.25 m，0.30 m，0.35m，0.40 m，波长L为8.5 m；（2）左面和右面为对称边界；（3）底部为固壁边界，满足无滑移边界条件；（4）出口和顶部为压力出口边界，忽略大气压的影响。

3.1 网格质量检查

本文采用四面体网格，单元网格的整体尺寸为0.2 m，对两个沙坝的单元格进行局部加密，尺寸为0.1 m。考虑壁面边界层及沙坝对流动的影响，将贴壁网格进行加密。同时，为了适当减小计算量，提高计算精度，在贴壁区域设置了边界层网格，最大层数为5层，边界层的增长率为1.2，过渡比为0.272。网格总数量为1 516 831个。

单元网格质量指标的范围为0～1，越接近1，表示网格质量越好。本次数值模拟的网格的平均质量为0.851 82，大于0.7，基本符合数值模拟计算要求。

3.2 波的适用性检查及模型可靠性验证

波陡 ς =H/L（波高与波长的比值）决定波形，ς越大，则波峰越陡峭，波谷越平坦；二阶Stokes波不适用于相对水深h/L＜0.125的情况，且Ursell数[20]Ur的适用范围为0～25，通过对式（17）的求解，结果如表1所示，可见4种不同波高情况下都满足该适用范围。

表1 不同波高的Ursell数Table 1 Ursell number of different wave heights

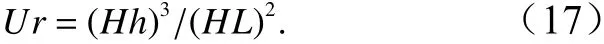
在有限深水二阶Stokes波浪理论中，其周期公式为

由式（17）可知，波浪周期与波高无关，只与静水深度h和波长L有关，g取9.8 m/s2， π取3.14，理论周期T通过式（18）计算出为2.60 s。图3给出了造浪边界处不同波高下3个周期内的波形，表征了液面高度随时间的变化情况，随着波高的增加，自由液面 η的高度也增加，但是周期均为2.58 s，与理论周期的误差小于1%，表明了此次数值模拟工作的可靠性。

图3 液面高度随时间的变化Fig. 3 The height of the liquid level varies with time

4 结果分析

4.1 离岸流水动力过程流场特性

不同波高情况下离岸流的水动力学分布不具有特殊性，仅仅影响离岸流的强度，现以波高H=0.35 m的仿真结果为例进行分析。

为了更清楚地看到离岸流发生时离岸方向（X）和沿岸方向（Z）速度分布的形态和演化的规律，根据定量的结果再次审视离岸流水动力过程的循环体系（图1），因此，重点分析沟槽附近的流体域的速度分布云图，将X、Y、Z方向的瞬时速度的分量分别记为u、v、w。

4.1.1瞬时结果

图4 和图5分别给出了0T、1/4T、1/2T、3/4T时刻离岸方向（X）和沿岸方向（Z）的速度云图。为了更好地分析结果，这里只显示沙坝附近的流场。在0T时刻可以清晰的看到离岸流的流头结构，该时刻波浪刚好到达沙坝附近，还没有翻过沙坝。在X=16 m处，波浪受到离岸流的冲击，向近岸区一侧发生凹陷；在1/2T时刻向深海区一侧凹陷。对比同时刻的速度w可知，离岸流受到波浪的阻挡后，分成两股水流沿着平行于海岸的方向流去，但是由于波浪的影响，其速度会逐渐减小。

图4 1个周期内离岸方向（X）速度云图Fig. 4 Velocity cloud distribution of offshore direction (X) velocity in a period

图5 1个周期内沿岸方向（Z）速度云图Fig. 5 Velocity cloud distribution of coastal direction (Z) velocity cloud map in a period

从不同时刻沿岸方向速度的分布（图5）来看，在X=5～7 m的区域，其速度大小较为稳定，区域分布比较广泛。沙坝外侧处的水流作为离岸流的供水源头，沿着两个沙坝，源源不断的汇聚到沟槽内，进一步发展成为离岸流。在X=7～15 m的区域有两对符号相反的速度结构，缺口处产生的一对符号相反的w速度结构是由于流颈变窄，速度变大，压强变小而带动周边流体补充所致，可见离岸流在形成过程中也会从周围流场积聚流体；流头处则是因为流体积聚，速度变小，压力增高，将海水向两侧排挤所致。

波浪必然与离岸流相互影响，相互制约。如图6所示，提取一个液相的体积分数为25%的等值面（该等值面一定程度上可以代表自由液面），分别取0T、1/4T、1/2T、3/4T4个不同时刻，观察波浪传播的情况以及该等值面上X方向的速度分布情况，可见波浪和离岸流之间的耦合作用明显。由于离岸流的影响，波浪传播到沙坝附近时，沟槽处的速度分布发生断层，可见离岸流在自由液面也并不是稳定存在的。波浪越大，则沙坝内侧汇聚的水流越多，形成的离岸流的强度也越大，会对波浪的冲击有一定的弱化作用。

图6 波浪表面速度u 分布Fig. 6 Offshore velocity u distribution of wave surface

4.1.2时均结果

由瞬态结果可得，离岸流并不是一个能持续稳定存在的流动，因此对其进行时均分析也非常必要。图7a给出了时均场X方向速度u=0.2 m/s的等值面图，可以清晰地看到流头和流颈的三维包络结构。在流颈部分，越靠近海底，其包络面的范围也越来越小，呈现出上宽下窄的倒三角形结构。图7b给出了速度w=-0.15 m/s 和w=0.15 m/s的等值面图，呈现出了两对反向排列的结构。可见，岸边海水沿着海岸向沙坝较高处移动，然后向离岸方向运动，继而在沙坝的阻碍下，沿着沙坝内侧向沟槽处移动，形成如图7b中箭头所示的水循环，构成了离岸流的主要供水源头，这与房克照等[21]实验结果中对离岸流补偿流的描述基本一致。该水循环结构与传统认知的离岸流的循环（图1）有所区别，体现在两点：（1）近岸岸边的水循环系统共同构成补给流；（2）流头是一个“铁锹式”下沉结构，主要是由于流头处的水流速度较低，表面容易受到波浪的影响；由此不难分析，向岸流不是一股具体的流动结构，而是海浪向岸边质量输运的综合效果，只是经由沟槽的海浪携带海水经自由海面流向岸边，构成近岸区水循环的来源。

图7 离岸流流场特性的三维结构Fig. 7 The 3-D structure of rip current

由于自由液面的速度分布出现了断层，为了探究不同水深下流速的分布情况，观察自由液面以下离岸流速度分布是否也产生了断层。研究中选取了压强P为1 000 Pa、3 000 Pa、7 000 Pa和8 000 Pa等4个等压曲面来分析，压强越大，则表示越远离自由液面，亦可反映海面波浪对海面下等压面形态产生的影响。同时，在该研究背景下同一竖直方向上压强大小与海水深度呈现正相关，不同等压曲面亦可反映距自由液面的水深情况。不同等压面上的时均速度分布如图8所示，可见，越靠近自由液面，其速度越容易受到波浪的影响，导致发生断层。

图8 不同等压面上u¯ 分布Fig. 8 The velocity distribution of u¯ under different isobaric surfaces

为了定量地分析不同流层的速度，现依次选取Y=0.9 m、Y=1.1 m、Y=1.3 m和Y=1.5 m 4个不同平面（Y=0 m为海滩底部），沟槽中心（即Z=8 m处）处时均速度随位移变化如图9所示，Y=0.9 m、Y=1.1 m和Y=1.3 m 3条曲线表明越接近海滩底部，由于水的黏性增大，其离岸流的速度越小；Y=1.5 m所在的平面为初始液面，由于受到波浪的冲击，其表面的离岸流的强度有所降低。水流在通过了沟槽（X=6 m）后，继续向离岸方向流动，速度进一步发展，形成流颈。在接近沙坝的沟槽（X=7 m）附近，速度最大，方向为正，即背离海岸指向外海。这股离岸流在受到向岸波浪的作用后，速度开始衰减，强度逐渐减弱。

图9 不同流层随离岸方向变化Fig. 9 The velocity distribution of at different flow layer along the offshore direction

为了更进一步说明波流耦合作用和水黏性的影响，选择流颈附近的一条竖直垂线（平面X=10.2 m和平面Z=8 m的交线），其平均速度随Y方向变化关系如图10所示。在Y=1.4 m的平面，即初始液面0.1 m下的位置是离岸流强度最大的位置，随着水深的进一步增加，上下水体交换越来越弱，离岸流强度也随之减弱。

图10 流颈附近随水位变化Fig. 10 The velocity distribution of near the neck of rip current varies with the water level

4.2 波浪高度对离岸流强度的影响

在研究了波浪高度H=0.35 m情况下离岸流的形态后，进一步改变入射波波高，分析波浪高度对离岸流的影响。图11和图12分别给出了速度u沿着离岸方向变化和速度w沿着沿岸方向的变化情况。其整体的趋势是随着波高的增加，两个方向的速度大小也增大。由图11可以看出，在X=7 m和X=12 m附近分别达到了极大值，表明了沟槽口附近离岸流的速度最大，此处为流颈处流速最快的位置，在受到波浪影响的情况下，速度在X=12 m附近达到了第2个极值。图12中取的是液面以下20 cm处靠近海岸的沟槽附近的速度曲线，该曲线关于Z=8 m呈现出反对称的趋势，表明其水流都沿着海岸朝着沟槽内流动，成为离岸流的供水源头。图13给出了沟槽附近（X=8.25 m）沿岸方向的时均速度分布规律，在Z=8 m处，其速度峰值随着波高的降低而降低，表明了离岸流的强度也随之降低。