基于SAR图像速度聚束调制的海浪反演研究

许荞晖，张彦敏*，王运华,2

( 1. 中国海洋大学 信息科学与工程学院，山东 青岛 266100；2. 青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室，山东 青岛 266237)

1 引言

海浪是海洋动力学的重要组成部分，海浪信息对于海洋工程、近海结构设计和航海以及理解和预测恶劣的海洋天气都是至关重要的。由于合成孔径雷达（SAR）成像过程不受天气和光照的影响，基于SAR图像的海浪反演技术已成为全天时、全天候、大面积海浪观测的主要途径之一。合成孔径雷达的海浪成像机制主要包括3种调制作用：倾斜调制、流体力学调制以及速度聚束调制[1-3]。其中，倾斜调制是由于大尺度海浪斜率改变了雷达局地入射角度，从而引起了回波强度的变化；流体力学调制则是由于大尺度海浪轨道速度所引起了Bragg共振波振幅的变化，进而导致雷达回波强度的变化；速度聚束调制则是SAR所特有的，是由于海浪的雷达视向速度导致海面散射面元沿SAR图像方位向发生位置偏移，进而引起回波强度沿着雷达方位向产生辐聚辐散效应[4-8]。以上3种调制是SAR图像海浪谱反演算法的基础，1991年，Hasselmann和Hasselmann[9]基于倾斜调制、流体力学调制和速度聚束调制，推导给出了SAR图像谱和海浪谱之间的非线性映射关系，并基于初猜谱与SAR图像谱构建价值函数，通过不断迭代计算使价值函数最小，从而获取最优海浪方向谱。1994年，Brüning等[10]为提高效率，对迭代求逆过程进行了改进。1996年，Hasselmann等[11]进一步改进了成像过程中非线性映射关系。2000年，Mastenbroek和De Valk[12]提出了基于Hasselmann所得非线性映射关系的半参数化海浪谱反演方法。2005年，Schulz-Stellenfleth等[13]则在MPI方法基础上，应用交叉谱提出了PARSA （Partition Rescaling and Shift Algorithm）海浪谱反演算法，该算法可有效解决海浪谱180°模糊问题。2010年，Zhang等[14]在He等[15-16]提出的海浪斜率谱极化调制算法基础上，利用全极化的Radarsat-2数据分别反演了海浪沿SAR图像方位向和距离向的海浪斜率谱，进而求取了海浪参数，该方法有效消除了流体力学调制的影响，但是，当入射角较小时，水平极化图像和垂直极化图像之间的差异较小，从而导致新构建图像中的海浪纹理变弱，从而不利于海浪反演。

近年来，基于SAR图像回波散射系数及截断波长等参数的海浪有效波高、主波波向等的经验化反演算法也引起了广泛关注。2007年，Schulz-Stellenfleth 等[17]提出了CWAVE经验化算法，由于这种方法主要是针对ERS SAR数据开发的，所以也称作CWAVEERS算法，该算法可直接反演得到海浪有效波高和平均波周期。在CWAVE基础上，后来不同学者又相继提出了针对其他卫星SAR数据的经验算法，例如适用于ENVISAT ASAR数据的CWAVE_ENV算法[18]，适用于Sentinel-1 SAR数据的CWAVE_S1A算法[19]和适用于Terra SAR-X数据的XWAVE算法[20]等。2015年，Romeiser等[21]则针对飓风极端海况条件下，建立了一种海浪有效波高与NRCS之间的经验函数来反演有效波高。2016年，Shao等[22]和Grieco等[23]则分别提出了关于有效波高和截止波长[24-25]、雷达入射角、海浪传播方向之间的半经验化关系。需要说明的是：基于海浪参数与SAR参数之间经验关系的反演算法，并不能得到海浪谱。

本文首先对比分析了倾斜调制、流体力学调制和速度聚束调制对SAR海浪图像的影响，结果表明，当海浪传播方向在偏离SAR距离向的过程中，3种调制因素中速度聚束调制对海浪SAR图像的影响始终最为显著。基于此，文中建立了基于速度聚束调制海浪方位向斜率反演算法，进而基于经验关系提取海浪有效波高。通过将Radarsat-2数据海浪反演结果与浮标数据相比较，本文反演算法较MPI算法和同极化调制函数算法反演结果的误差更小。

2 影响SAR图像的调制因素的比较

2.1 调制因素影响的理论分析

在线性调制理论的框架下，海面高度 ζ(r,t)和后向散射截面 σ(r,t)随大尺度海浪的变化均可表示为线性叠加的形式[9]，即

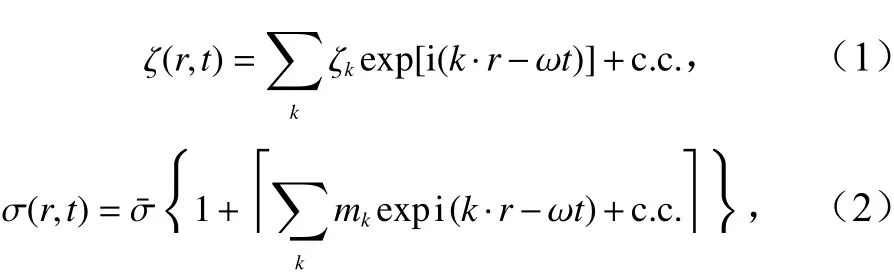
对于垂直极化（VV），倾斜调制函数为

式中，θ为雷达入射角；kl是雷达视向上的大尺度海浪波数分量。流体力学调制传递函数可根据短波与长波相互作用的双尺度模型推导得出[28]

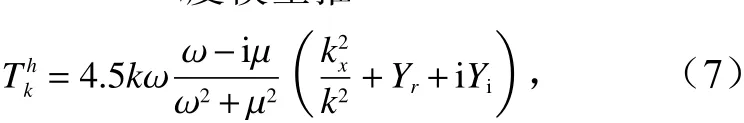
式中，μ为阻尼系数；Yr+iYi为 负反馈因子；kx是海浪波数距离向分量。

对于实孔径雷达，定义归一化图像强度为

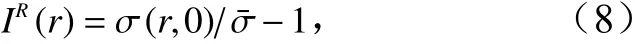
于是结合式（2）和式（8）可得IR(r)图像的傅里叶变换系数为

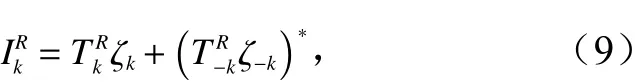
进而可得，IR(r) 图 像谱与海浪谱Fk的关系为[9]

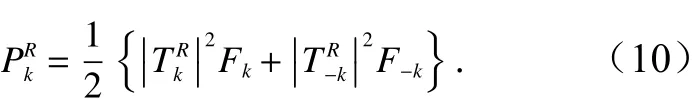
然而，对于海浪SAR图像而言，海浪运动所引起的速度聚束效应非常显著，在线性条件下，考虑到速度聚束效应的影响后海浪归一化SAR图像的傅里叶变换系数为[9]

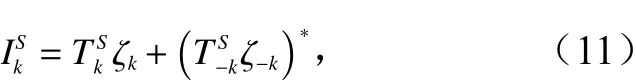
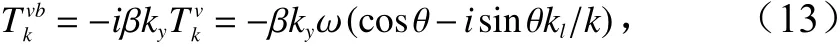
式中，β=R/V，其中R为斜距；v为SAR平台飞行速度；ky是大尺度海浪波数沿雷达方位向的分量。

由于SAR图像同时存在倾斜调制、流体力学调制、速度聚束调制3种调制因素，基于式（11），可将海浪归一化SAR图像的傅里叶变换系数分解为为仅考虑实孔径雷达调制的傅里叶变换系数为仅考虑速度聚束调制的傅里叶变换系数，二者分别为

图1 仿真海面SAR图像（a），仅考虑速度聚束调制的海面SAR图像（b）和仅考虑倾斜调制和流体力学调制的海面SAR图像（c）Fig. 1 Simulated SAR image of sea surface (a), simulated SAR image of sea surface with the velocity bunching modulation (b) and simulated SAR image of sea surface with the tilt modulation and the hydrodynamic modulation (c)

图2 a至图2c则给出了图1中3幅海面SAR图像所对应的图像谱。通过图像谱可以看出，仅考虑速度聚束效应影响的图像谱（图2b）与考虑3种调制的海面仿真SAR图像谱（图2a）的谱值在同一数量级，而仅考虑倾斜调制和流体力学调制影响的SAR图像谱（图2c）的谱值则小得多。另外，从谱的形态上，仅考虑速度聚束效应影响的图像谱与考虑3种调制的海面仿真SAR图像谱更为相近。

2.2 实测海面SAR图像调制因素影响分析

为了进一步验证图1和图2所示的结果，我们采用真实的SAR卫星数据进行分析。本文后续使用的实验数据为Radarsat-2 SAR数据，Radarsat-2 SAR具有高分辨率多种极化通道的成像能力，本文中使用的Radarsat-2 SAR数据为超精细全极化模式数据，方位向分辨率为4.73 m，距离向分辨率约为4.9 m，表1为本文所用到的所有数据目录，图3给出了一幅Radarsat-2 数据2 SAR图像的总体位置示例。

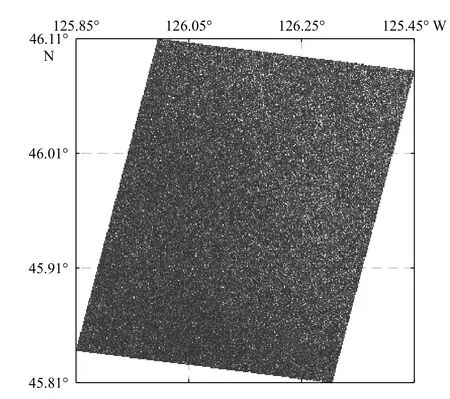
图3 Radarsat-2数据2的SAR图像Fig. 3 SAR image of Radarsat-2 data 2

图4 和图5中基于Radarsat-2真实测量SAR数据进了不同调制因素的影响分析，这里选用SAR图像来自表1中的数据2。图4a为截取的512×512个像素大小的HH极化归一化SAR图像，图4b为仅考虑速度聚束调制时的归一化SAR图像，图4c则是仅考虑倾斜调制和流体力学调制影响的归一化SAR图像。由图可见，对于真实SAR海面图像而言，所得结果与图1仿真结果所得结论相一致，即：仅考虑速度聚束调制影响的归一化SAR图像与考虑3种调制的归一化SAR图像的强度和海浪纹理非常接近，而只考虑倾斜调制和流体力学调制影响的SAR海面图像的强度值明显偏低且海浪纹理并不明显。图4中3幅海面SAR图像对应的图像谱分别如图5a至图5c所示，图5中的结果与图2仿真SAR图像的结果一致，仅含有速度聚束调制影响的SAR图像谱（图5b）与原SAR图像谱（图5a）的谱形状和谱密度都非常接近，而仅包含倾斜调制和流体力学调制影响的图像谱（图5c）的谱值就小得多，且峰值位置与原SAR图像谱相比有一定的偏离。

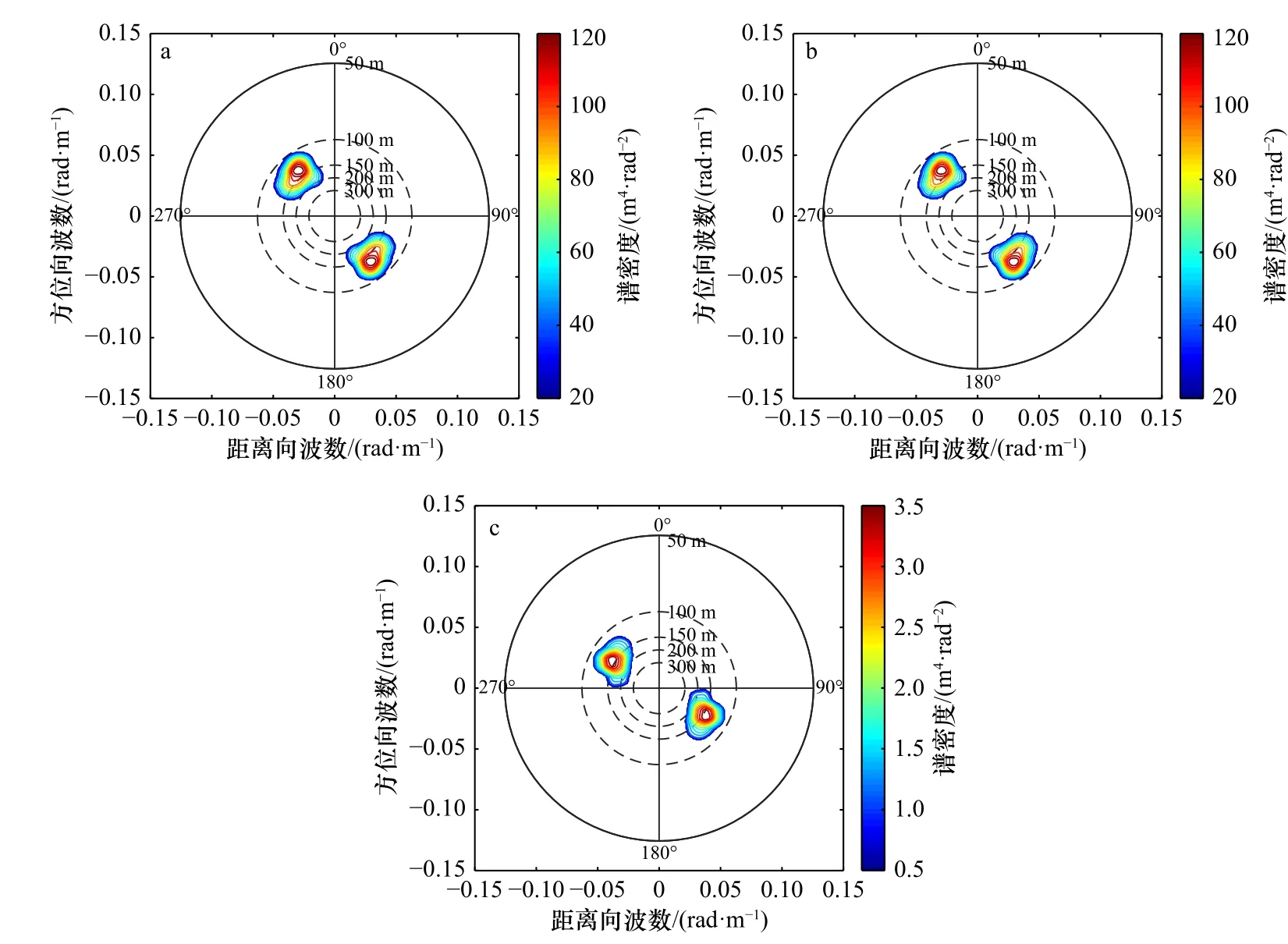
图2 仿真海面SAR图像谱（a），仅考虑速度聚束调制的仿真海面SAR图像谱（b）和仅考虑倾斜调制和流体力学调制的仿真海面SAR图像谱（c）Fig. 2 The spectrum of the simulated SAR image of sea surface (a), the spectrum of the simulated SAR image of sea surface with the velocity bunching modulation (b) and the spectrum of the simulated SAR image of sea surface with the tilt modulation and the hydrodynamic modulation (c)

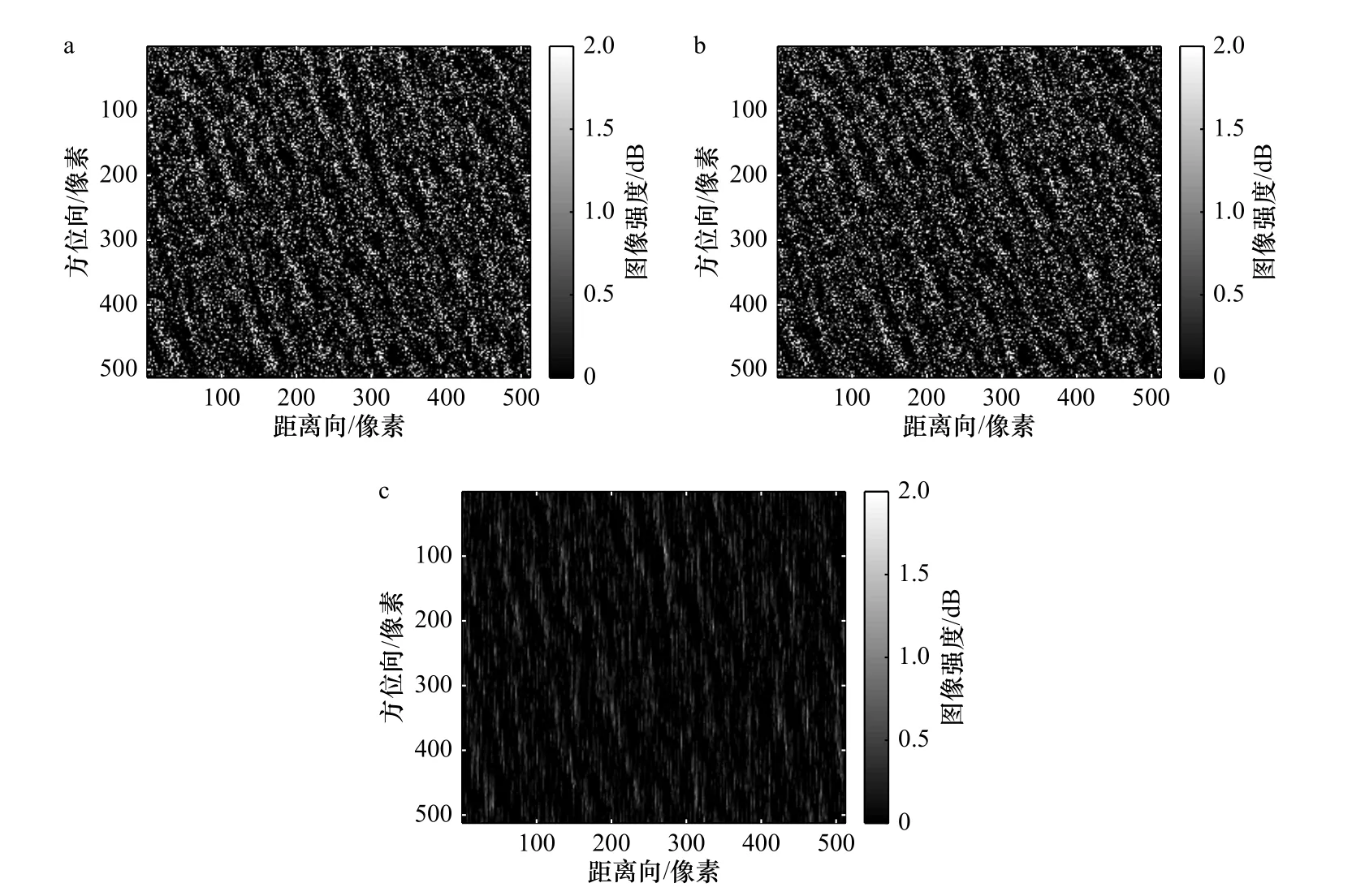
图4 Radarsat-2数据2中选取的512×512像素SAR图像（a），仅考虑速度聚束调制的SAR图像（b）和仅考虑倾斜调制和流体力学调制的SAR图像（c）Fig. 4 SAR image of 512×512 size selected in Radarsat-2 data 2 (a), SAR image that only the velocity bunching modulation is considered(b) and SAR image that only the tilt modulation and the hydrodynamic modulation are considered (c)

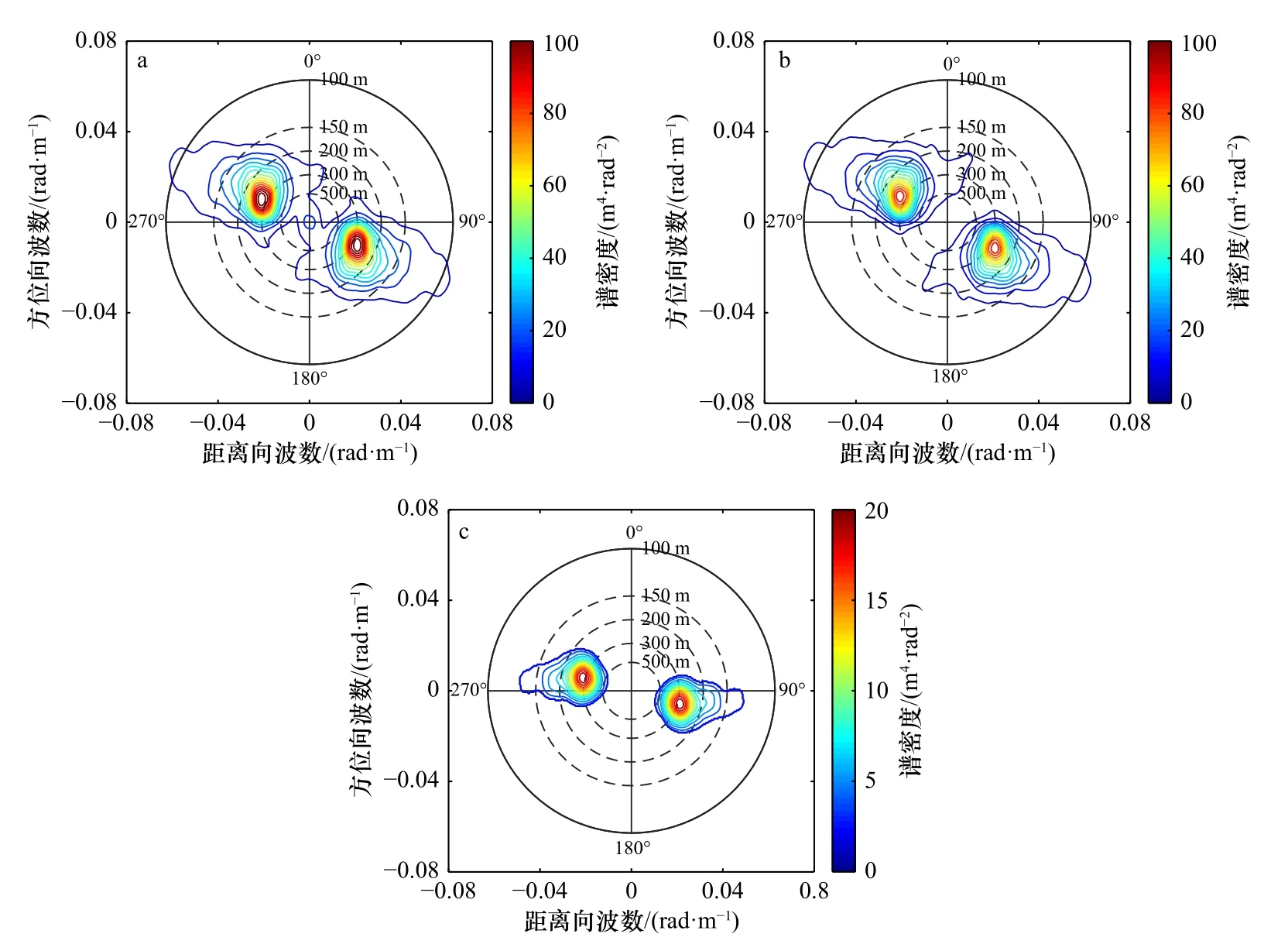
图5 SAR图像谱（a），仅考虑速度聚束调制的SAR图像谱（b）和仅考虑倾斜调制和流体力学调制的SAR图像谱（c）Fig. 5 The spectrum of the SAR image (a), the spectrum of the SAR image that only the velocity bunching modulation is considered (b)and the spectrum of the SAR image that only the tilt modulation and the hydrodynamic modulation are considered (c)

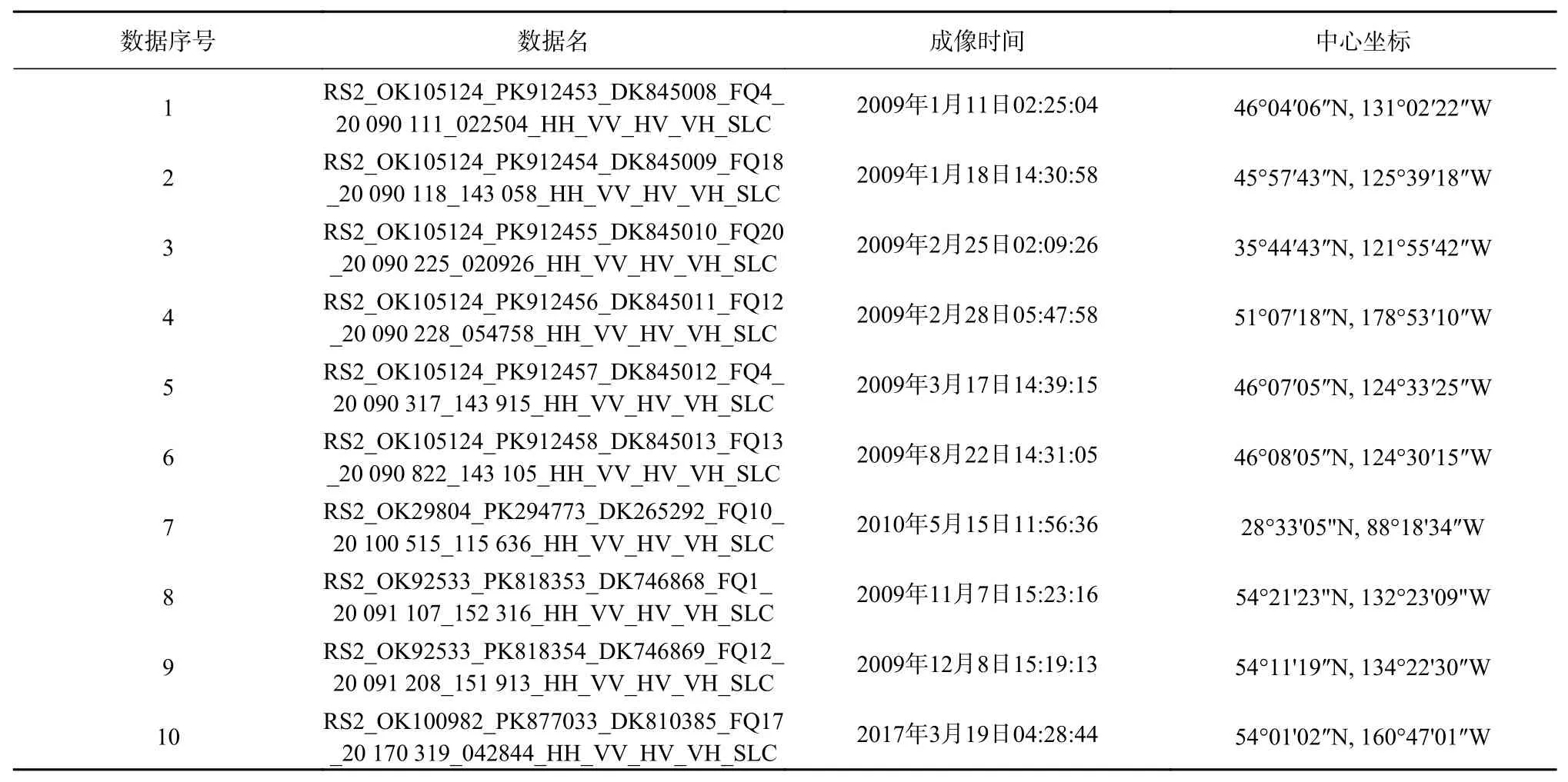
表1 Radarsat-2全极化SAR数据信息Table 1 Radarsat-2 full polarized SAR data information

2.3 海浪不同传播方向时的调制因素比较

为了进一步分析不同海浪传播方向时各调制函数对SAR图像的影响，我们仿真不同涌浪传播方向角（与距离向的夹角分别为0°、15°、30°、45°、60°、75°、90°），其他参数同图1情况下的海面SAR图像，进而将考虑3种调制效应的归一化SAR图像谱、仅考虑速度聚束调制效应的归一化SAR图像谱与仅考虑倾斜调制和流体力学调制时的归一化SAR图像谱等3种谱的积分能量进行了比较。图6a为给出考虑不同调制因素时图像谱积分能量随海浪传播方向的变化，图6b则为仅考虑速度聚束调制时的SAR图像谱积分和仅考虑倾斜调制和流体力学调制影响时的SAR图像的谱积分能量分别占考虑3种调制效应的图像谱能量的比重。由图可见：在海浪传播方向角远离距离向的变化过程中，仅考虑速度聚束调制的SAR图像谱积分能量和考虑3种调制效应的图像谱积分能量呈现上升趋势，而且通过图6b可以看出，仅考虑速度聚束调制影响的SAR图像谱积分能量占考虑3种调制效应的SAR图像谱积分的比重不断增大，而且总保持在70%以上。实孔径调制（倾斜调制和流体力学调制）对SAR图像的影响随着海浪传播方向与距离向的夹角的增加呈现出减小趋势，而且倾斜调制与流体力学调制影响下的图像谱积分能量较考虑3种调制效应的SAR图像谱积分能量来说所占比重较小，基本都在20%以下。以上结果进一步表明速度聚束调制对SAR图像纹理的影响远大于倾斜调制和流体力学调制的影响。

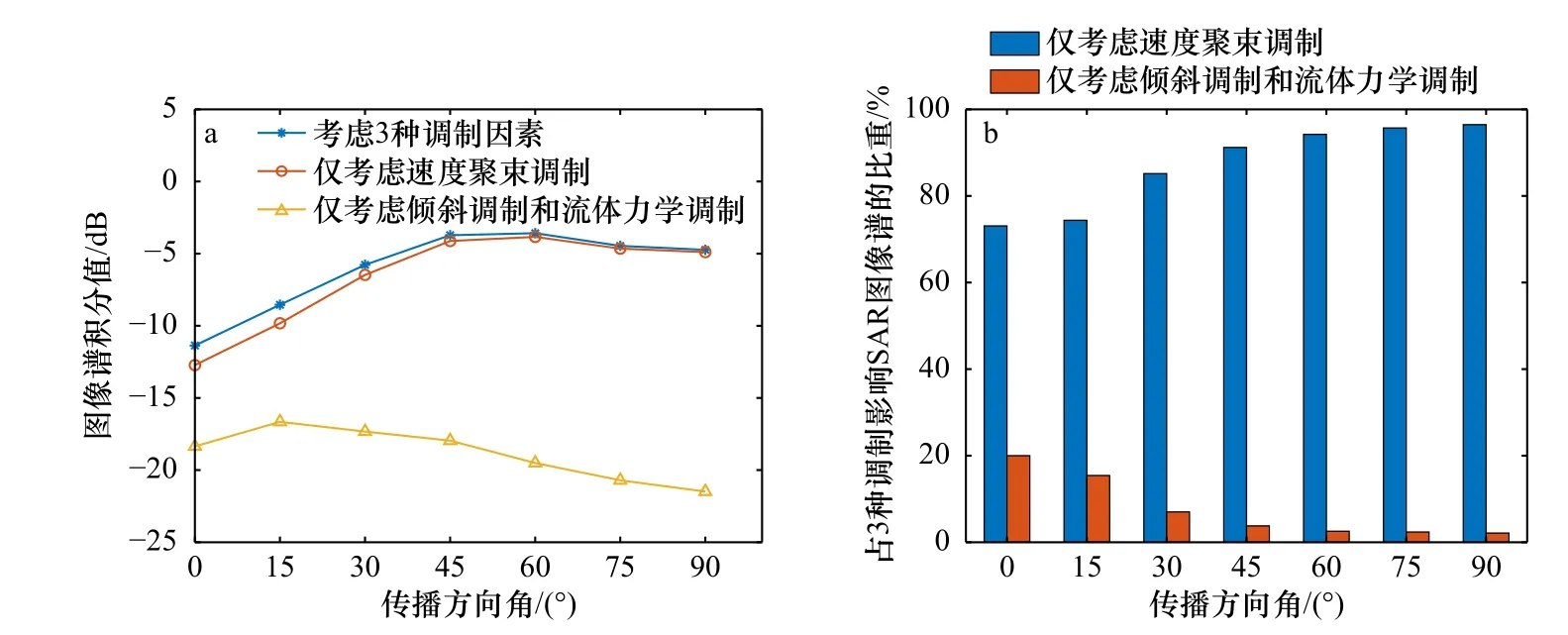
图6 仿真SAR图像谱积分能量随涌浪传播方向角的变化（a），在不同传播方向角下，考虑不同调制的谱积分能量占总能量的比重（b）Fig. 6 The spectral integration value variation of the simulated SAR images with different wave propagation direction angle (a), the proportion of the spectral integration variation under the different modulation conditions with different wave propagation direction angles (b)

通过上述结果我们发现在SAR成像过程中，速度聚束效应对SAR图像中海浪纹理的影响远大于倾斜调制和流体力学调制的影响。通过式（5）、式（7）、式（12）可知，海浪沿方位向的波数只要稍微有所增大，此时，由于β的值较大，从而导致影响非常显著，相比较而言，倾斜调制和流体力学调制的影响则非常小。

3 相干斑噪声影响

在海浪反演过程中相干斑噪声的影响也是不可忽视的。Arsenault 和 April[29]证明了相干斑噪声是乘性独立同分布的。因此在空间域时，一般采用的相干斑噪声模型可表示为[30-32]

式中，I是观测到的SAR图像中像素点的强度；x是相应的真实反射强度；乘性噪声n满足Gamma分布，其均值为1，并且对于均匀区域它的标准差σn为[28]

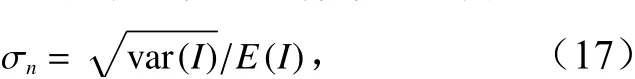
式中，var( )表示求随机变量的方差；E( )表示求随机变量的均值；对于单视图像来说，方差σn为1。据此对模拟的二维海面回波信号（图7a）添加乘性噪声如图7b所示。

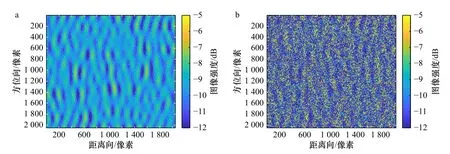
图7 未添加（a）和添加（b）乘性噪声的二维海面回波信号Fig. 7 Two-dimensional echo signal of ocean wave without (a) and with multiplicative noise (b)

为分析乘性噪声对图像谱的影响，将未添加乘性噪声和添加乘性噪声的二维信号的图像谱进行比较，图8中给出沿着方位向波数平均的平均功率谱密度，可以看出添加乘性噪声后的所得功率谱密度要高于未添加乘性噪声的平均功率谱密度。对于基于SAR图像的海浪反演算法而言，尤其值得关注的是：在图像谱的低波数区域，乘性噪声引起了功率谱的增大，此时基于调制函数直接进行海浪反演时，根据Hasselmann海浪谱与图像谱的映射关系可知，乘性噪声在低波数区必将引起显著反演误差[9]。

图8 沿方位向的平均图像谱密度Fig. 8 Mean density of image spectrum along azimuth direction

4 基于速度聚束调制的SAR图像海浪反演

目前，在Hasselmann海浪谱反演算法中，由于Bragg理论并不能准确反映海面回波随大尺度海浪斜率的变化，因此，基于Bragg理论所得海浪倾斜调制函数并不准确；此外，流体力学调制至今也尚不成熟。然而，通过前面的分析可见，相对于倾斜调制和流体力学调制而言，速度聚束调制对SAR图像纹理特征的影响起主导作用，这使得单纯基于速度聚束调制的海浪谱反演算法所得海浪参数可能更为准确。另外，通过上一节讨论可知，相干斑会给SAR图像谱带来影响，尤其是低波数范围内的噪声会导致海浪谱的反演产生显著误差，为减小该因素的影响，我们基于速度聚束调制反演海浪方位向斜率谱。

由式（1）可得，海面沿方位向斜率可表示为

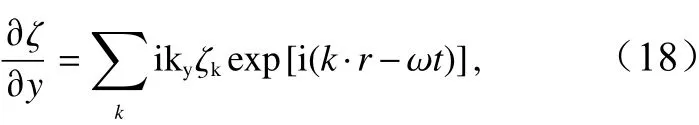
式中，ky代表方位向波数。根据SAR图像海浪调制理论，仅考虑速度聚束调制影响时的归一化SAR图像可表示为

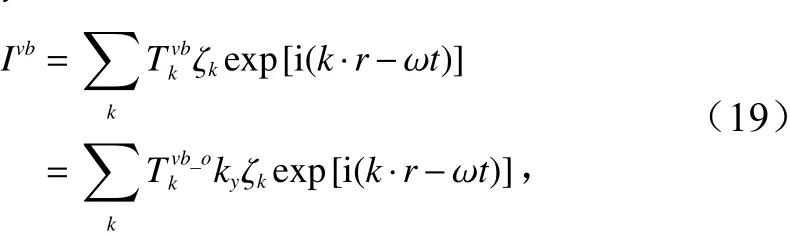
式中，

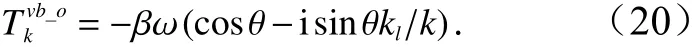
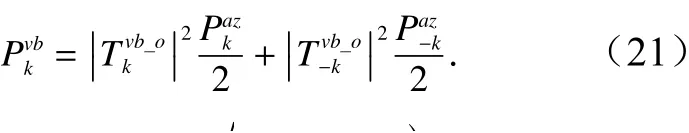
根据斜率谱可求主波波长为

式中，kp为主波波数，主波周期为

当海浪并非严格地沿距离向传播时，海浪斜率均方根

式中，σas为方位向斜率均方根；ϕ表示海浪传播方向与距离向的夹角；有效波高HS可以通过主波波长和斜率均方根求出[14]

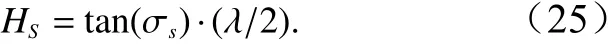
图9 中分别给出了基于数据2和数据3 SAR图像选取的一块子图像反演所得海浪方位向斜率谱。图9a中为数据2 SAR图像基于速度聚束调制反演所得斜率谱，计算得到的有效波高为3.39 m，主波波长为256.74 m，海浪传播方向与方位向夹角为63.23 °。图9b中，反演所得到的有效波高为2.18 m，主波波长216.85 m，传播方向角为126.69 °。一般情况下，对于开阔海域中的海浪而言，在统计意义上相近海域的海浪是一样的，因此，在整幅SAR图像中选取一块区域反演所得海浪谱与SAR图像中其他区域反演所得海浪谱具有相似性。为了更好地说明这一情况， 作为示例，我们基于数据2和数据3两幅SAR图像的整幅图像对海浪谱进行了反演，所得结果为图10a和图10b，将图10反演结果与图9中选取SAR子图像反演结果进行对比可见：整幅图像与局域图像反演所得海浪谱的形状、有效波高、主波波长和传播方向等趋于一致。

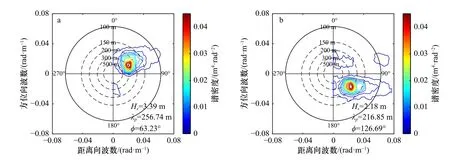
图9 Radarsat-2数据2（a）和数据3（b）中 SAR子图像反演所得方位向斜率谱Fig. 9 The azimuth slope spectrum retrieved from the sub-image of SAR in Radarsat-2 data 2 (a) and data 3 (b)

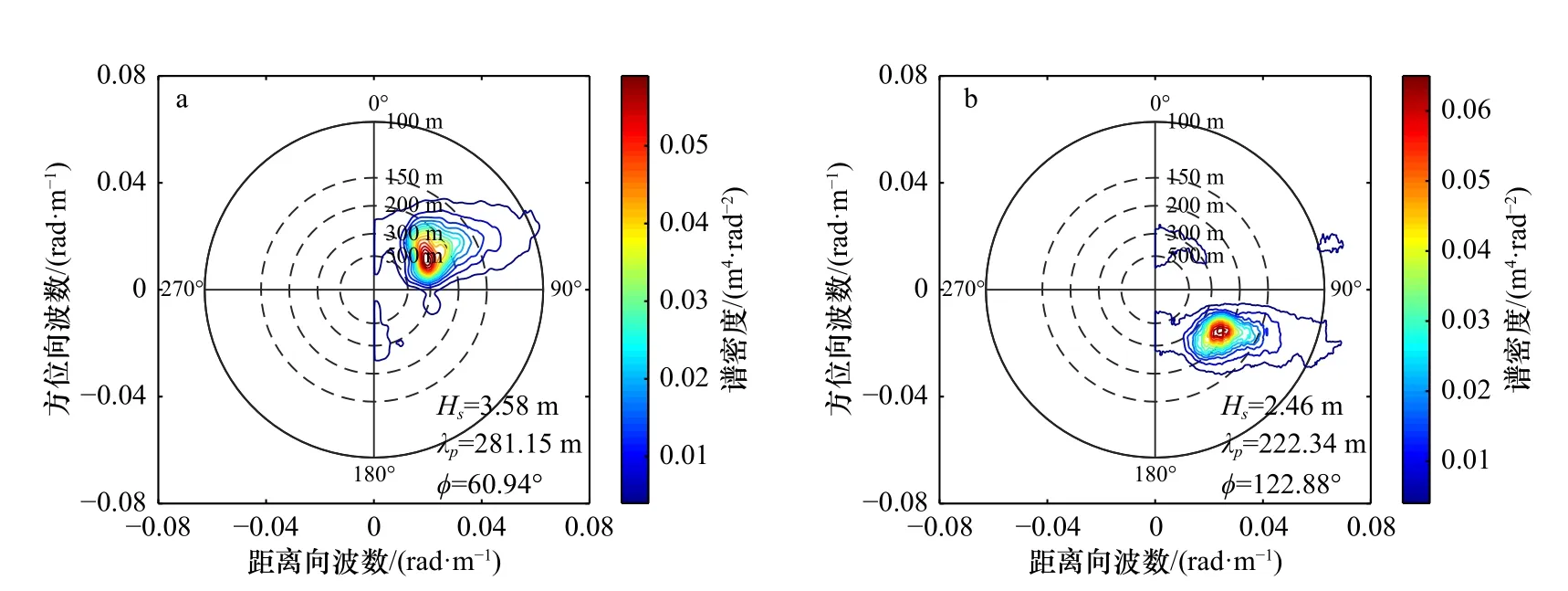
图10 Radarsat-2数据2（a）和数据3（b）整幅SAR图像反演所得方位向斜率谱Fig. 10 The azimuth slope spectrum retrieved from the SAR in Radarsat-2 data 2 (a) and data 3 (b)

为验证本文方法反演结果的有效性，我们将表1中10景Radarsat-2 SAR数据反演所得结果分别与浮标数据和ECMWF再分析数据进行了对比，结果如表2所示，作为比较，表2中还给出了MPI法和同极化调制函数法反演所得结果，为了减少对外部数据的依赖，在MPI法中尝试将通过SAR图像谱和海浪谱的一阶线性映射关系得到的海浪谱作为初猜谱进行输入。3种不同反演方法所得有效波高与浮标观测结果对比的散点图如图11所示，与ECMWF再分析有效波高数据的对比散点图见图12。在与浮标实测数据对比的图11中，红色散点和红色实线分别代表本文方法反演所得有效波高及其拟合线，反演所得波高的均方根误差为0.79 m，拟合线斜率为1.13；绿色散点和绿色实线分别为MPI方法反演的有效波高结果及其拟合线，其均方根误差为1.47 m，拟合线的斜率为0.44；蓝色散点和蓝色实线代表同极化调制函数法反演的有效波高结果及其拟合线，该方法所得结果的均方根误差为1.46 m，拟合直线斜率为0.62。通过与ECMWF再分析数据对比的图10可以看出，其结果的整体趋势与图9中一致，并且本文方法反演所得波高的均方根误差0.92 m也为3种方法中最小。通过图11和图12不同方法反演结果的对比分析，可见：与MPI方法和同极化调制函数法反演的有效波高相比，利用本文算法反演斜率谱进而计算得到的有效波高的误差更小，与浮标实测数据对比的拟合直线斜率更接近1。但是需要说明的是：当海浪沿距离向传播时，由式（24）可得，本文方法不再适用，而同极化调制函数法则仍适用。

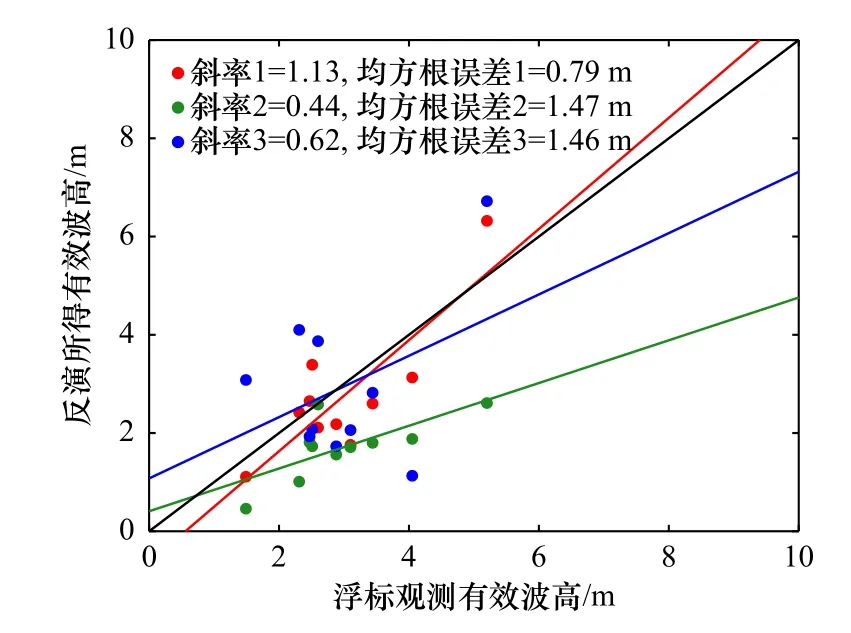
图11 不同方法反演有效波高与浮标观测结果对比散点图Fig. 11 The scatter plots of retrieved significant wave height by different methods with buoy data

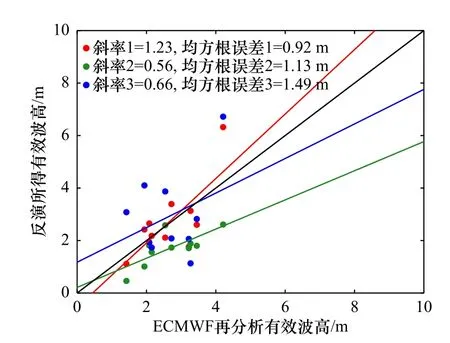
图12 不同方法反演有效波高与ECMWF再分析数据对比散点图Fig. 12 The scatter plots of retrieved significant wave height by different methods with ECMWF reanalysis data

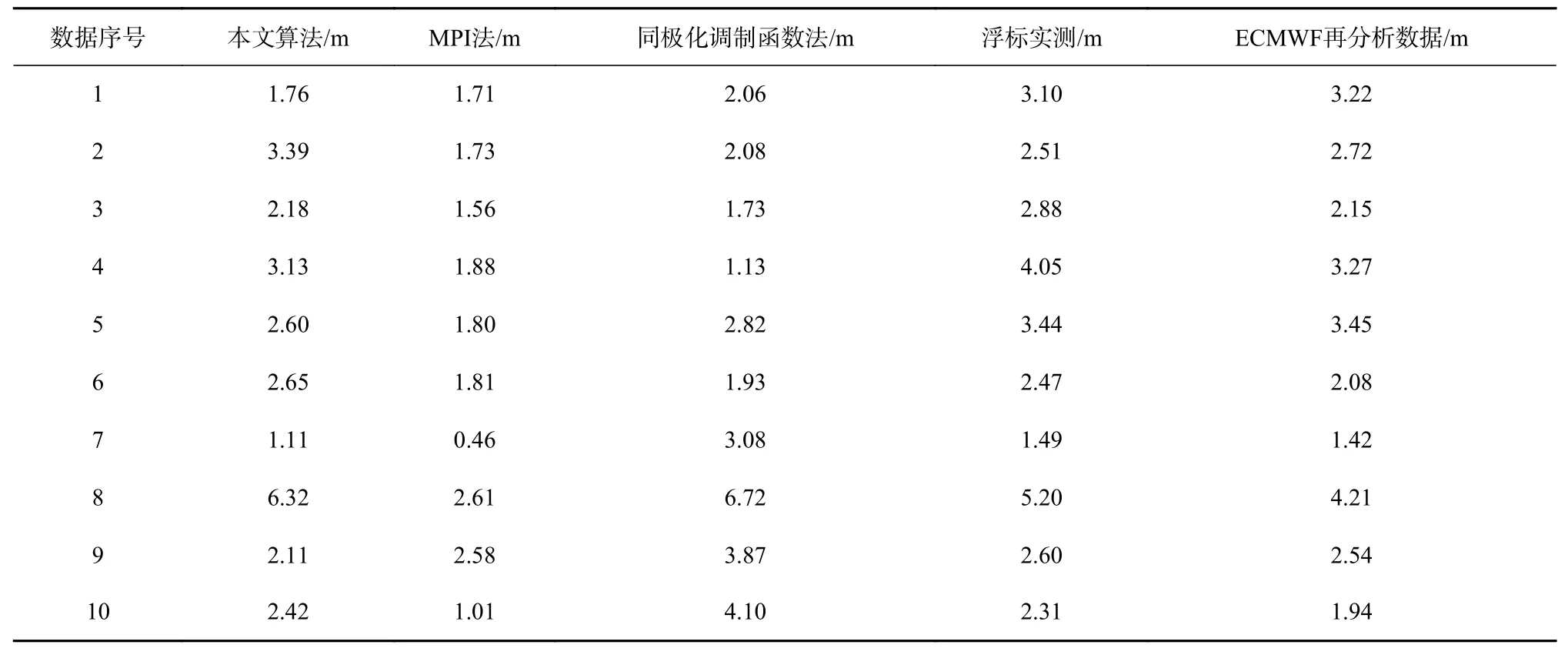
表2 Radarsat-2数据不同反演方法的有效波高结果Table 2 The retrieved significant wave height of different inversion methods for Radarsat-2 data

5 结论

本文首先分析了海面SAR图像中倾斜调制、流体力学调制和速度聚束调制3种调制函数的影响，将考虑不同调制函数的SAR图像分别提取对比，并在不同海浪传播方向情况下统计分析比较，结合理论分析，发现速度聚束调制在3种调制中对SAR图像的影响尤为显著，远大于倾斜调制和流体力学调制的影响。通过对相干斑噪声的影响分析发现相干斑噪声对海浪SAR图像反演有一定影响，特别是在低波数区域相干斑噪声对反演结果的影响显著，基于此，我们利用只考虑速度聚束调制的SAR图像直接反演方位向斜率谱的方法以降低相干斑噪声的影响。通过比较，可得：本文算法反演所得有效波高结果较MPI方法和同极化调制函数法所得结果与浮标数据和ECMWF再分析数据吻合更好。与Zhang等[14]提出的全极化斜率谱反演算法不同的是，本文算法是基于单极化SAR数据，从中提取出仅考虑速度聚束调制影响的SAR图像反演海浪方位向斜率谱。然而，需要说明的是：当海浪沿距离向传播时，本文反演海浪有效波高的方法不再适用。