库水变动下水库滑坡变形预测研究

程江涛

中化地质矿山总局湖北地质勘查院，湖北 武汉 430075

水库滑坡是岸坡内地下水动力学条件改变而产生的一种地质灾害，主要发生在水库建设与运营期间，由水位上升、水位骤降或降雨等导致[1]。水库滑坡是我国三峡库区较为常见的一种地质灾害，据不完全统计，三峡库区范围存在体积大小不等的各类滑坡、崩塌体约2490处，其中在175m水位范围内的滑坡体约有1630处[2]，占不稳定斜坡体数量的65.5%。大量滑坡的存在势必给三峡水库的正常运营带来巨大的安全隐患，其变形失稳的危害主要体现在两个方面[3-4]：①滑坡失稳形成的大量岩土体涌入水库内，导致水库不能正常运营；②高速滑入水库内的岩土体将会产生巨大涌浪，当滑坡体位于近坝库岸时，由涌浪产生的巨大冲击荷载将可能导致大坝在瞬间垮塌，同时涌浪波及范围内的城镇居民往往来不及转移，给库区人民的生命财产造成严重损失。

国内外有关水库滑坡失稳的实例屡见不鲜：1963年10月发生于意大利瓦依昂（Vajont）水库左岸巨型滑坡，20s内有超过 2亿 m3的滑体以28m/s的速度飞越宽约 80m的河谷，造成水库下游约2600人死亡，同时滑体将坝前 1.8km范围内的库容全部填满，导致整个瓦依昂水库完全报废[5]；2003年7月发生于三峡库区支流青干河左岸的千将坪特大型岩质滑坡，约有1500万m3滑体在5min内滑入水库内，导致14人死亡，10人失踪，造成的直接经济损失高达8000多万元[6-7]。以上典型事例表明，水库滑坡失稳造成的后果往往是灾难性的。

水库滑坡一直是水利水电工程与工程地质领域研究的热点与难点问题，并得到了广大学者与业内人士的高度重视[8-9]：在1992年召开的第六届国际滑坡专题研讨会议上，水库滑坡的稳定性问题被作为一个重点进行了专题讨论[10]；2002年ICOID为水库滑坡的勘察与评价建立了专门的分析指南[11]。滑坡的变形预测预报问题的难度就更大，滑坡变形监测资料是反映内外系统相互作用的有效信息来源，如何通过监测资料揭示滑坡内外因素相互作用的过程是滑坡变形预测的关键。自 1968年日本学者斋腾迪孝提出基于蠕变破坏三阶段的经验预报模型以来，经国内外学者近40余年的苦心探索，已开拓出以统计分析、非线性科学、系统综合分析以及实时动态跟踪为理论基础的综合预测预报模型[12-15]。

在已有研究中存在以下几方面问题：①基于岩土体微观变形机制的力学预测模型是建立在室内物理力学试验基础上的，由于滑坡是一个离散体，位于不同空间部位的土体其物质组成与结构是不同的，与之相对应的力学变形机制也是不同的，采用离散部位的室内试验结果代替复杂的滑坡系统显然只适用于均质土坡；②基于时序分析的统计预测模型是建立在滑坡变形监测信息基础上的，由于变形监测信息中不仅包含有滑坡内动力物质系统产生的变形，而且还包含有滑坡外动力激励系统产生的变形，而外动力激励系统是一个随机的系统，单纯依靠时序监测数据建立的预测模型显然难以反映滑坡变形演化的内在机理；③基于滑坡变形来源机制的动力成因预测模型是建立在滑坡变形影响因素基础上的，能较好反映滑坡内外系统相互作用的过程，但针对水库滑坡开展这方面的预测模型研究却较为少见，需进一步进行深入研究。

本文以李家湾滑坡为研究对象，以实测的变形监测数据为基础，利用逐步回归分析的数学方法，试图从影响因素与变形之间的相关性上来构建滑坡的变形预测模型。通过研究，不仅能为水库滑坡的变形预测提供一些新的思路，同时为三峡库区水库滑坡的防灾减灾及监测预警提供一些行之有效的方法。

1 滑坡概况

李家湾滑坡位于长江左岸斜坡地带，距三峡大坝坝址71.73km，行政区划隶属巴东县东瀼口镇旧县坪村一组。地理坐标为：X 3437798，Y 37439310；E 31°03′34″，N 110°21′51″。研究区内主要的地表水系为自西向东横穿巴东县中部的长江水系，西起边域溪河口，东至牛口入秭归县境，流经县境长约38km，多年平均流量4487.7 亿 m3。

滑坡区地处长江北岸，地形地貌类型属构造剥蚀中低山峡谷地貌，地势总体上呈现出北东高、西南低的空间分布特征。滑坡后缘高程300m，前缘最低高程90m左右，相对高差约210m。坡体中部200～210m高程处修筑有雷太公路，公路上部切坡地段形成4～8m高的陡坡（图1）。李家湾滑坡区出露的地层主要为中生界中三叠统巴东组第二段（T2b2）陆相层状碎屑岩地层和第三段（T2b3）浅海相碳酸盐岩地层，以及上覆新生界第四系（Q4）松散堆积层。

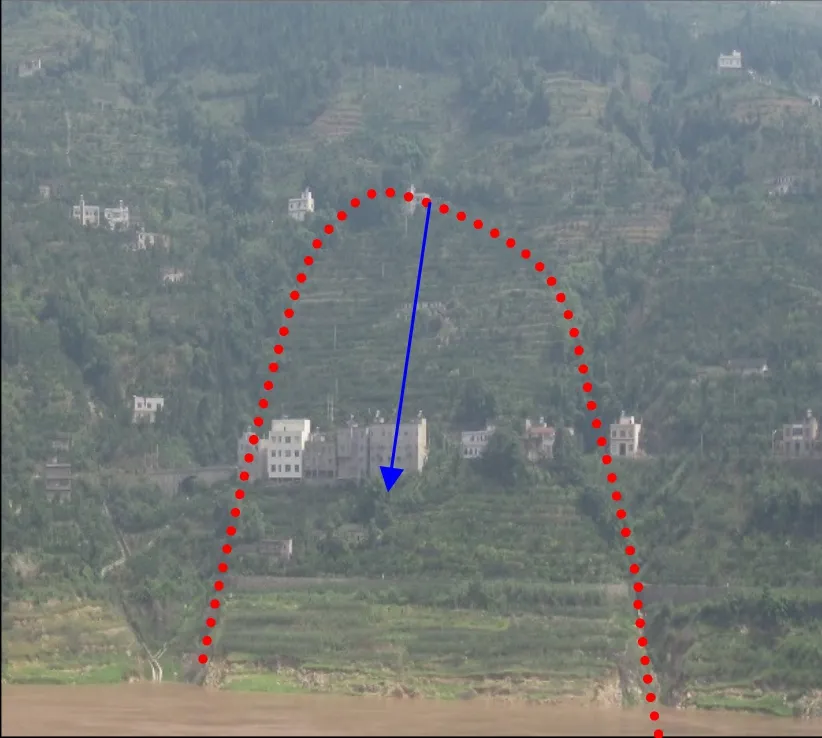
图1 滑坡全貌图Fig.1 Landslide panorama

2 回归分析模型

滑坡变形监测分析的目地主要有两方面：一方面是了解滑坡变形的主要影响因素；另一方面是找出滑坡变形的演化规律及其发展趋势，在遇到异常情况时能及时发出安全警报，以确保滑坡周边建筑物及居民的安全。目前，大多数滑坡变形预测模型都是建立在位移数据的时序分析和数学构造基础上的，未能考虑滑坡变形影响因素的作用效果，而工程实践中大多数滑坡的位移突变都是由影响因素的作用引起的。为此，有必要从滑坡变形影响因素的角度来建立滑坡变形的预测模型。

按照影响因素作用方式的不同可将滑坡变形分为两部分，一部分是由滑坡内动力物质系统控制的以大时间尺度表现的时效变形，该类变形通常具有不可逆性；另一部分是由滑坡外动力激励系统控制的以小时间尺度表现的随机变形，该类变形通常具有可逆性，对于水库滑坡而言，影响滑坡变形的外动力激励因素主要有库水变动和大气降雨两种。为此，可通过时效[16]、库水位和降雨量[17]三个影响因子来构建滑坡的变形预测模型[18]，其表达形式如下：

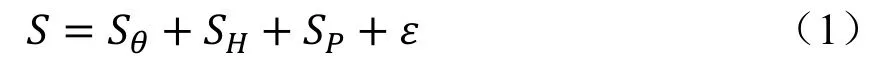
式中：S为滑坡总变形量，mm；Sθ为时效变化引起的变形分量，mm；SH为库水位变化引起的变形分量，mm；SP为降雨量变化引起的变形分量，mm；ε为统计常数，可通过回归分析得到。

2.1 时效引起的变形分量

时效变形是由滑坡内动力物质系统作用所产生的那部分变形，一般由不同时刻滑坡体所受的自重应力和抗滑阻力所决定，该类变形具有不可逆性，其大小与滑坡体所经历的累积时间相关，通常可用多项式模型来表征，其具体函数如下：

式中：θ为时效因子，为观测日期至基准时间的天数除以 100得到的值；a1、a2、a3为时效变化引起的变形分量回归系数。

2.2 库水位引起的变形分量

库水位变形是指由库水变动过程中的地下水水力学效应产生的那部分变形，一般由库水位涨落引起的水位差所决定，该类变形具有可逆性。已有的研究表明，库水位变化引起的变形可通过库水位涨落高差h的一、二、三次函数来表示，其中库水位变化引起的挠曲变形与h3有关，库水位变化引起的剪切变形则与h2有关，由水体自重引起的沉降变形与h有关[19]。考虑到库水变动作用对滑坡变形的滞后性，可通过指数函数构建该变形分量，具体如下：

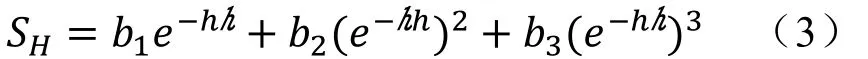
式中：h为库水位涨落高差，为观测当日的库水位与前期库水位之差除以100得到的值；b1、b2、b3为库水位变化引起的变形分量回归系数。

2.3 降雨量引起的变形分量

降雨量变形是指由降雨入渗过程中的地下水水力学效应产生的那部分变形，一般由降雨量引起的水头差所决定，该类变形具有可逆性。已有的研究表明[20]，滑坡发生前 1～2个月的有效降雨量均会导致滑坡变形的发展，为此可通过当前降雨量、前1月平均降雨量和前2月平均降雨量作为衡量该变形的指标。考虑到降雨入渗作用对滑坡变形的滞后性，可通过指数函数构建该变形分量，其具体形式如下：

式中：P0为观测日期当月平均降雨量除以100得到的值；P1为观测日期至前1月平均降雨量除以100得到的值；P2为观测日期至前2月平均降雨量除以100得到的值；c1、c2、c3为降雨量变化引起的变形分量回归系数。

通过上述三种变形分量构建的滑坡总变形预测模型如下：

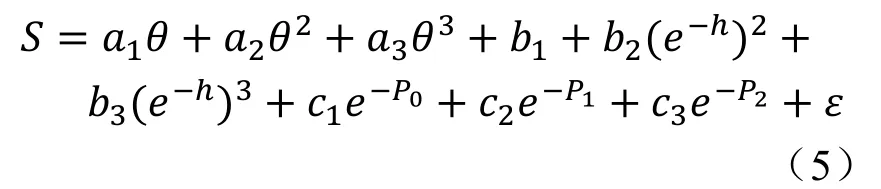
根据上述回归预测模型，结合实测的影响因子参数（自变量）和位移值（因变量），即可通过最小二乘原理获取上述回归系数，进而建立基于影响因子回归分析的变形预测模型。

3 逐步回归分析模型的求解

3.1 逐步回归分析的基本原理

回归分析是研究因变量y与自变量x=（x1，x2，…，xn）之间相关关系的一种数理统计方法。滑坡变形回归分析的目地不仅仅是建立因变量与自变量之间的函数关系，更重要的是抓住滑坡变形的主要影响因子。在多元回归分析中，对于不同自变量的组合，通常可以得到不同的回归方程，为此有必要从众多的影响因子中遴选出显著性的自变量，以建立最优的回归方程，同时该回归方程也能反映出滑坡变形的主要影响因子，逐步回归分析正是实现上述功能的一种有效统计方法。逐步回归分析主要通过两个方面得以实现：一方面，按自变量对因变量的显著性程度，按照从大到小的顺序逐个引入回归方程；另一方面，当先前引入的自变量由于后面自变量的引入而使得回归方程变得不显著时，就将该自变量剔除。由此可见，逐渐回归分析是分步进行的，在每一步回归分析过程中有时会引入自变量，有时则会剔除自变量，这取决于引入自变量对回归方程的显著性，即逐步回归分析中的每一步均要作统计检验，以确保回归方程中只包含显著因子。由于最终建立的回归方程中只包含显著性的自变量，因此其预测效果较好。

3.2 逐步回归分析的求解步骤

首先计算出各自变量之间的相关系数矩阵，初步分析各自量之间的相关性，观察自变量之间是否有多重共线性现象。假定初始回归方程为：

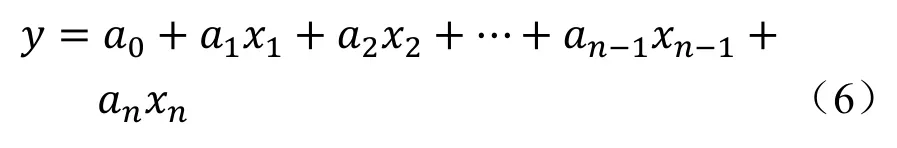
利用最小二乘法求得统计回归方程为：

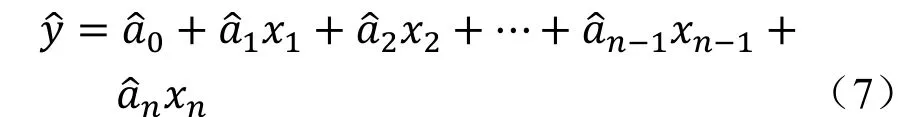
利用实测值与回归值计算初始模型的残差平方和为：

假定从初始回归方程中剔除x1自变量，则经过回归分析求得的新模型为：

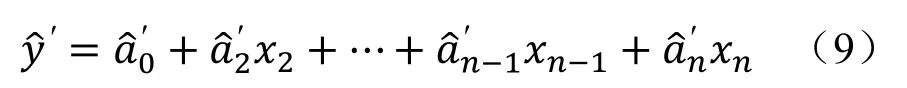
利用实测值与回归值计算新模型的残差平方和：

计算两个模型的残差平方和之差，该值反映了x1自变量对回归方程贡献的大小：

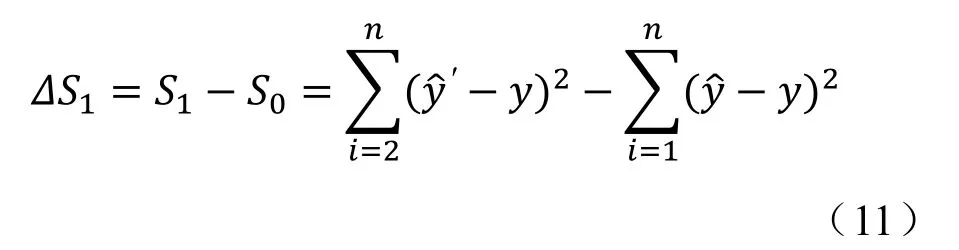
构造统计检验量，检验x1自变量对回归方程的显著性：

式中：k-观测次数；n-回归方程中自变量个数。

4 预测模型的建立与分析

4.1 建模数据的选取与处理

李家湾滑坡的变形监测资料显示，滑坡前部监测点的变形主要受库水变动的影响，滑坡中部监测点的变形则受降雨和库水变动的联合作用影响，滑坡后部监测点的变形则主要受大气降雨的影响。为研究不同影响因素作用下的滑坡变形预测模型，选取李家湾滑坡主剖面上的三个地表位移监测点（BDT-35、BDT-36、BDT-37）作为研究对象（图2，编号1、2、3分别代表BDT-37、BDT-36、BDT-35监测点），截取 2007-8-8～2009-7-13之间的25组监测数据作为样本，其中以2007-8-8～2009-2-13之间的20组监测数据作为建模样本，为检验模型的预测效果，以2009-3-13～2009-7-13之间的 5组监测数据作为预测样本，观测基准时间为 2007-8-8，各组样本的数据信息如表1所示。利用表中数据建立的变形影响回归因子如表2所示。

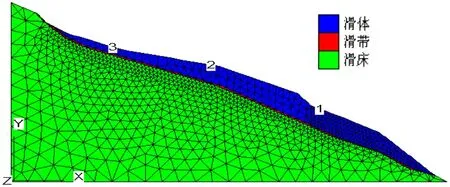
图2 滑坡数值计算模型Fig.2 Numerical calculation model of landslide

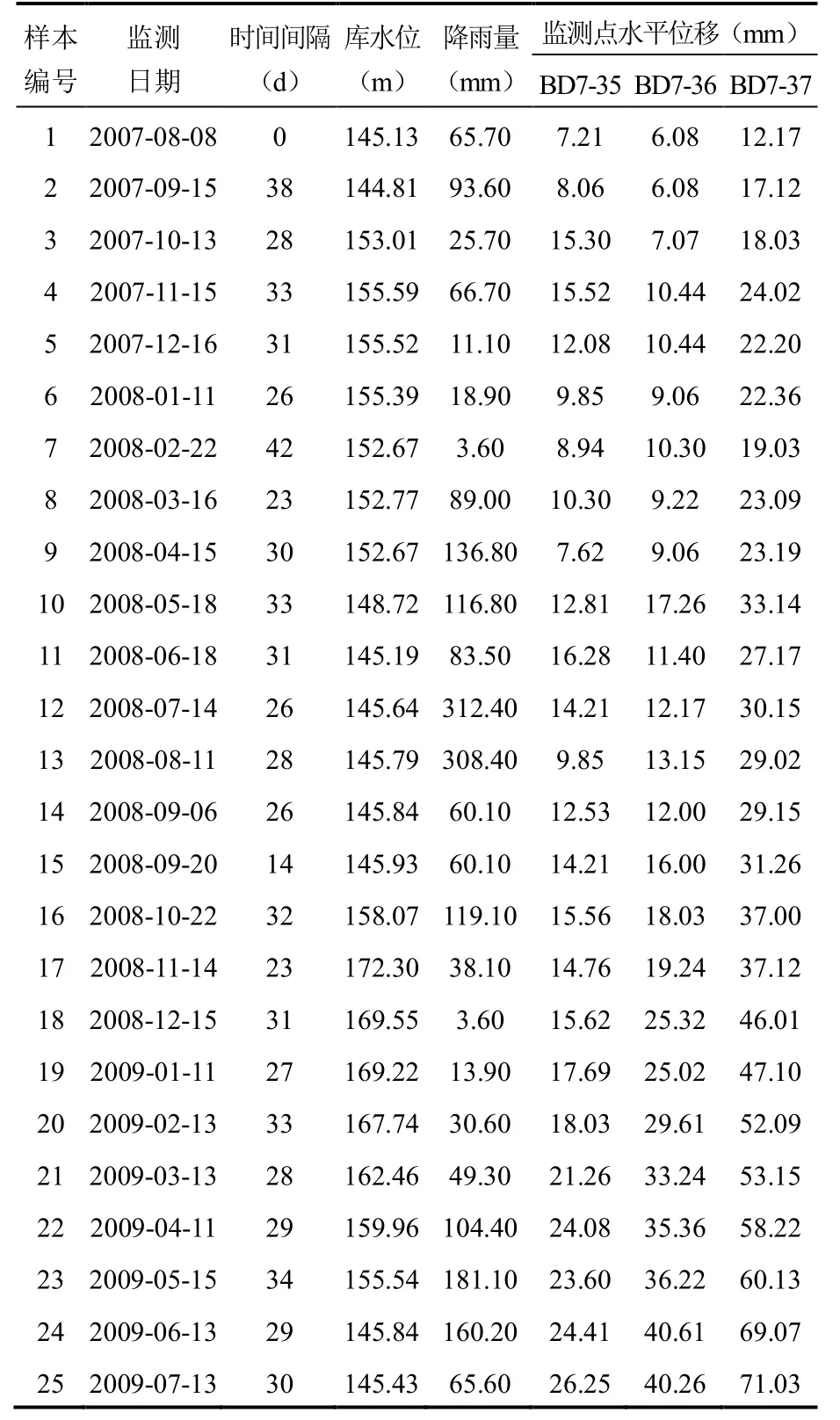
表1 建模样本数据Table 1 Modeling sample data

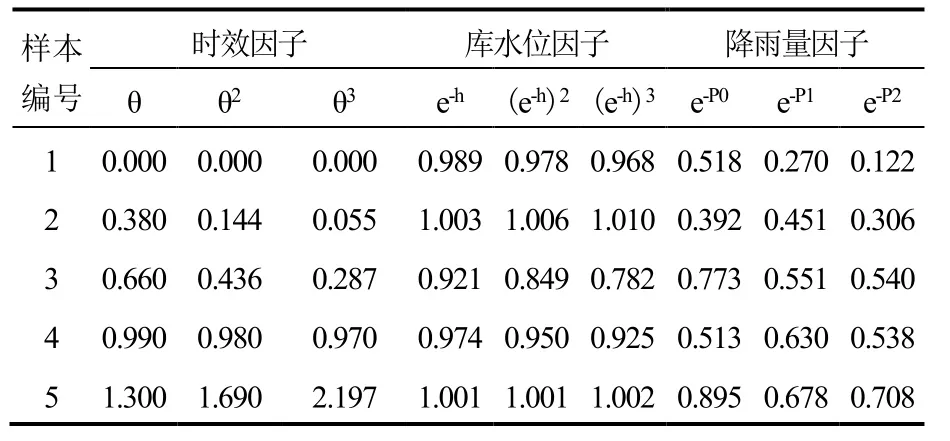
表2 影响因子参数Table 2 Influencing factor parameters

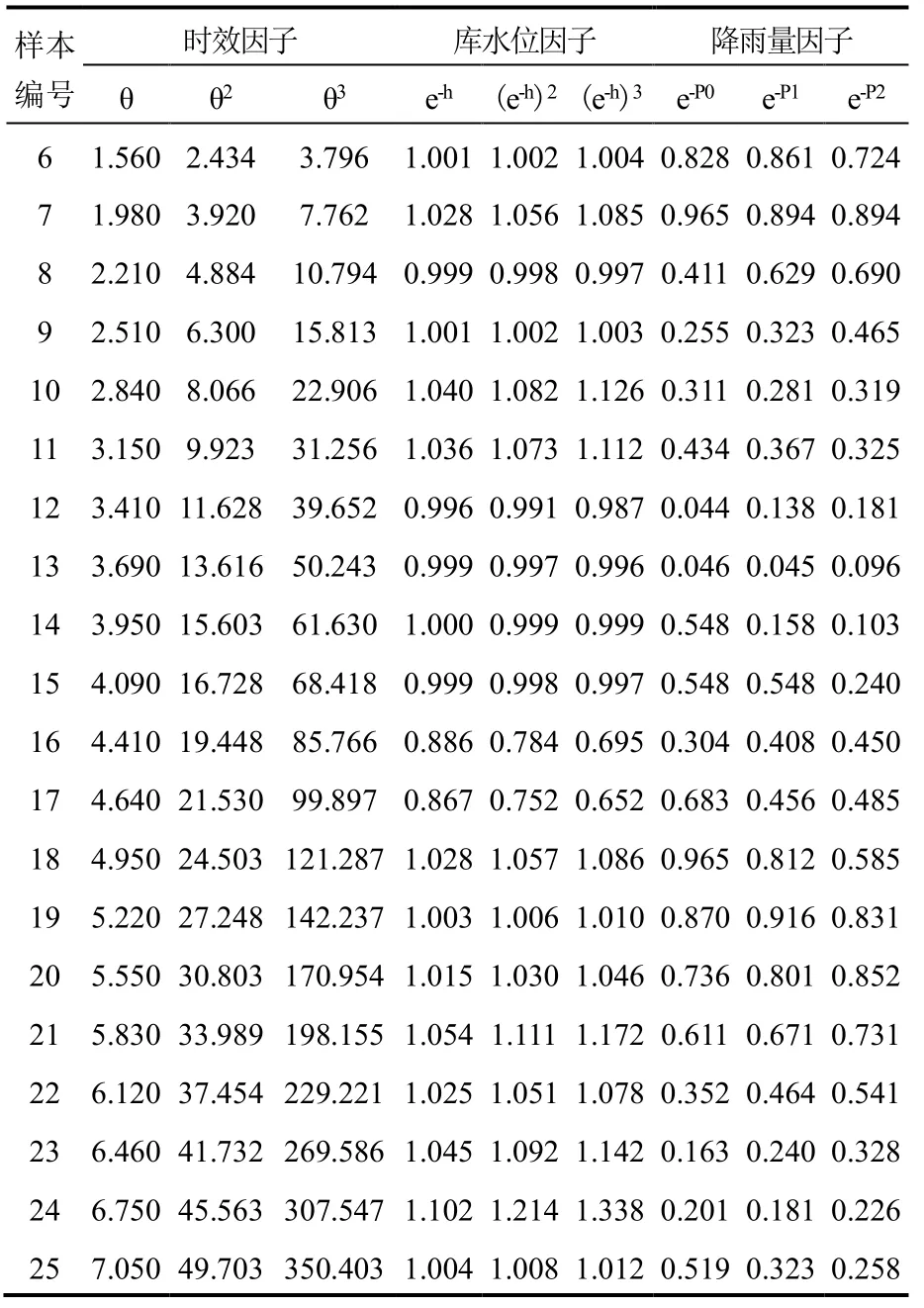
续表2

4.2 预测结果分析

4.2.1 滑坡后部 BDT-35监测点变形预测模型与影响因素分析

通过回归分析建立的 BDT-35监测点变形预测模型如下：

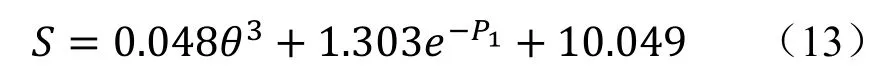
预测结果见表3。通过该表可以看出，基于影响因子分析建立的回归预测模型不仅能很好的拟合历史监测数据，而且其预测误差在 1.27%～10.1%之间，具有较好的预测效果，但基于模型的时效性，应不断利用新的监测数据建立新的回归预测模型才能保证预测的可靠性。

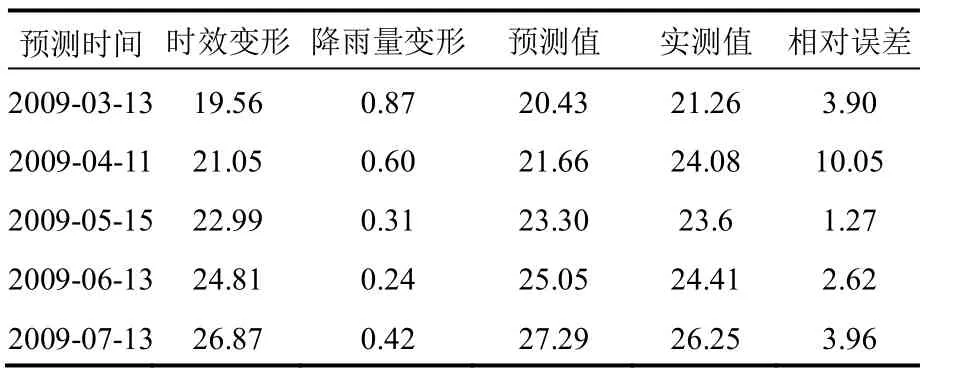
表3 BDT-35监测点水平位移预测成果表Table 3 Horizontal displacement prediction results of BDT-35 monitoring point

4.2.2 滑坡中部 BDT-36监测点变形预测模型与影响因素分析

通过回归分析建立的 BDT-36监测点变形预测模型如下：

预测结果见表4。通过该表可以看出，基于影响因子分析建立的回归预测模型不仅能很好的拟合历史监测数据，而且其预测误差在 0.41%～4.69%之间，具有较好的预测效果。

表4 BDT-36监测点水平位移预测成果表Table 4 Horizontal displacement prediction results of BDT-36 monitoring point

4.2.3 滑坡前部 BDT-37监测点变形预测模型与影响因素分析

通过回归分析建立的 BDT-37监测点变形预测模型如下：

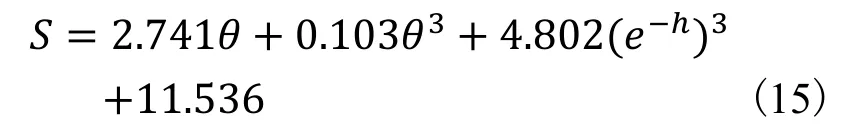
预测结果见表5。通过该表可看出，基于影响因子分析建立的回归预测模型不仅能很好的拟合历史监测数据，而且其预测误差在0.80%～3.90%之间，具有较好的预测效果，但基于模型的时效性，应不断利用新的监测数据建立新的回归预测模型才能保证预测的可靠性。

表5 BDT-37监测点水平位移预测成果表Table 5 Horizontal displacement prediction results of BDT-37 monitoring point

综上所述，李家湾滑坡后部BDT-35监测点的变形主要是由时效变形和降雨量变形引起的，且降雨量对该部位变形的影响较小；滑坡中部BDT-36监测点的变形主要是由时效变形、库水位变形和降雨量变形共同引起的，且降雨量对该部位变形的影响较库水位大；滑坡前部 BDT-37监测点的变形主要是由时效变形和库水位变形引起的。另外，从时效变形中影响因子的成分上看，BDT-35和BDT-37监测点变形回归方程中均含有θ3因子，而BDT-36监测点变形回归方程中含有θ2因子，这说明李家湾滑坡后部和前部滑体处于加速蠕变阶段，而中部滑体则处于匀速蠕变阶段，即滑坡中部滑带尚未贯通。

5 结论

（1）滑坡变形是滑坡内动力物质系统与外动力激励系统共同作用的结果，按照变形影响因素作用方式的不同可将其分解为时效变形、库水位变形和降雨量变形；其中时效变形反映内动力物质系统的作用，该变形具有不可逆性，是时间的函数，可用多项式函数来表征；库水位变形和降雨量变形反映外动力激励系统的作用，该变形具有可逆性，其中库水位变形是库水位涨落高差的函数，降雨量变形是前期1～2个月累计平均降雨量的函数，可用指数函数来表征，上述三种变形分量的组合即为滑坡的总变形。

（2）BDT-35监测点的变形影响因素主要为时效因子和降雨量变化因子，其中时效变形分量随着时间的推移呈现出三次方增长趋势；降雨量变形分量与前1个月的累积平均降雨量相关，其变化幅值仅为1.14mm，与该部位附近地下水位监测孔基本为干孔的事实相吻合。

（3）BDT-36监测点的变形影响因素主要为时效因子、库水位变化因子和降雨量因子，其中时效变形分量随着时间的推移呈现出二次方增长趋势；库水位变形分量在水位上升过程中产生趋向坡内的变形，在水位下降过程中产生趋向坡外的变形；降雨量变形分量与前2个月的累积平均降雨量相关，且降雨量变形分量的变化幅值较库水位变形分量大，与该部位附近地下水位监测孔为季节性孔的事实相吻合。

（4）BDT-37监测点的变形影响因素主要为时效因子和库水位变化因子，其中时效变形分量随着时间的推移呈现出三次方增长趋势；库水位变形分量在水位上升过程中产生趋向坡内的变形，在水位下降过程中产生趋向坡外的变形，与该部位附近地下水位监测孔与库水位具有一致性的事实相吻合。