基于差分进化的连续Hopfield神经网络模型参数优化

张伟丰

（湖北汽车工业学院 经济管理学院，湖北 十堰 442002）

连续Hopfield神经网络（continuous hopfield neural network,CHNN）解决组合优化问题是神经网络应用的重要方面，在实际应用中将优化问题的目标函数转换为连续Hopfield神经网络的能量函数，优化变量对应于网络中神经元的状态，当神经元状态趋于平衡点时，网络的能量函数趋于最小值，最终达到稳定状态，问题的最优解也随之求出，网络由初始值向稳态收敛的过程即目标函数优化计算的过程。由于神经网络是并行计算的，计算量不会随维度的增大而指数性增加，能有效进行快速优化计算。网络的优化效果受参数的影响较大，因此确定合适的参数是Hopfield神经网络需要解决的关键性问题。目前用优化算法对其他某些算法的参数进行优化来提高其性能的研究取得了较好的成果，文献［1-4］分别以改进的粒子群算法或蚁群算法优化支持向量机的参数，以便更好地解决分类问题。文中以此为借鉴，提出了以差分进化算法优化Hopfield神经网络的参数用来求解组合优化问题。差分进化算法进行优化计算时，以参数序列作为编码来表示个体，网络的能量函数作为适应度函数，以网络计算稳定后的能量值评价个体好坏，经过若干代进化操作后，选择种群中最优个体作为网络的参数，然后以搜索到的最佳参数构建网络对组合优化问题进行优化计算，实验表明，只要搜索到恰当参数，Hopfield网络均能稳定收敛，较快地求得最优解。

1 Hopfield神经网络求解TSP问题

连续Hopfield神经网络是单层结构的反馈网络，由n个神经元（N1,N2,…,Nn）组成，每个神经元既是输出单元也是输入单元，其输出作为其他神经元的输入，如图1所示。Hopfield网络优化计算的步骤描述如下：1）选择合适的问题表示方法，使神经元输出与问题的解对应；2）构造能量函数，使其最小值对应问题的最优解；3）由能量函数求得对应的权重和偏置参数；4）构造网络的动态方程；5）初始化网络，优化计算求解。

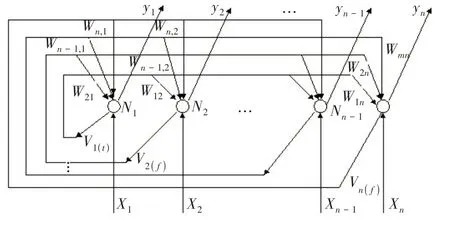
图1 Hopfield网络结构图

TSP问题是典型的组合优化问题，当城市个数增加时，计算量会激增，容易收敛到局部解或非法解。根据连续Hopfield网络优化计算特点，将TSP问题的目标函数即最短路径与约束条件和网络的能量函数对应，将经过的城市顺序与神经元状态对应，当网络能量趋于最小值时，神经元趋于平衡点，对应的城市顺序即最佳路径。

对于N个城市的TSP问题，采用N×N换位矩阵（各行和各列的和均为1的矩阵）来表示，需要用N×N个神经元来实现，考虑到所求解的实际意义，即换位矩阵的每行每列只有1个1，网络的能量函数由目标函数和约束项组成，定义如下：

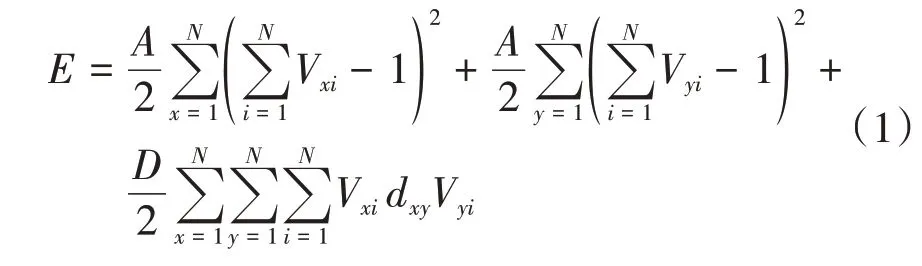
通过求导，网络的动态方程为

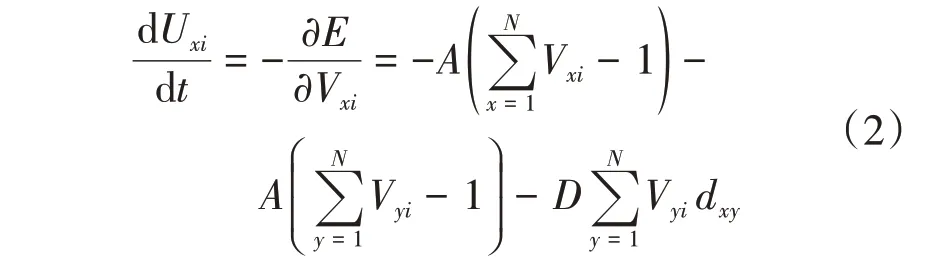
式中：A为能量函数的系数；D为动态方程的系数。根据研究经验，按式（3）对网络输入进行初始化：

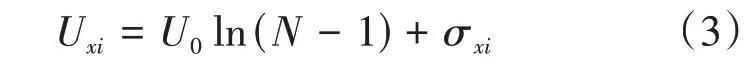
式中：N为城市个数；U0为方程系数；σ为[-1,1]的随机数。综上所述，需要优化的参数有A、D、U0和σ，找到合适的参数值对网络的计算至关重要。

2 DE-Hopfield算法模型及流程

2.1 编码

利用差分进化算法解决优化问题，首先需要解决编码问题，由于优化的是Hopfield网络参数，文中采用实数编码的方式，即直接以参数序列表示某个个体。需要优化的参数有4个，设Pt为第t代个体，编码表示为

在个体初始化时，根据给定的各参数的取值范围，分别产生给定范围的随机数，生成第1代种群。

2.2 适应度函数

适应度函数是评价个体好坏的标准，当个体分解为参数后，进入Hopfield网络的求解过程，以网络经过若干次计算后达到稳态后的最终能量函数值作为此个体的适应度函数，能量值越低，说明参数越合适，即个体越好。适应度函数可表示为式中：EHop为以此个体所代表的参数进行网络优化计算后的能量值。fitness取负数表示能量值越低，适应度越大。

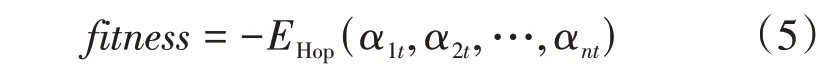
2.3 算法流程

算法输入为各参数搜索区间、TSP问题城市坐标值、种群大小、迭代次数；算法输出为最优参数、最低能量函数值、最优路径和最短距离。算法如下：1）对需要优化的参数A、D、U0、σ，根据以往的经验设置各自搜索区间，设置种群大小，随机初始化种群，设置最大迭代次数K,记录最优个体gBest；2）对种群中每个个体进行差分变异操作，按照前述的择优保留方式保存变异操作后的个体；3）对每个个体进行交叉操作，同样保留较优个体；4）步骤2）和步骤3）择优保存时需要进行适应度的计算，适应度即个体所代表的参数进行网络优化计算后的能量函数值，计算网络优化后的能量值；5）从种群中选择适应度最优个体，保存在gBest中，判断是否达到K，如果达到，算法结束，输出gBest及其对应的参数，最佳路线和最短距离，否则转步骤2）。

网络优化后的能量值计算步骤如下：1）读取城市坐标数据，并计算各城市间的距离，根据个体编码解析出网络参数，初始化网络，设置最大迭代次数k；2）利用式（2），用一阶欧拉法计算

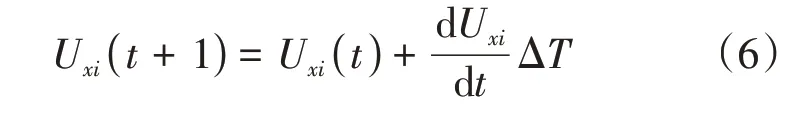
3）计算网络输出为

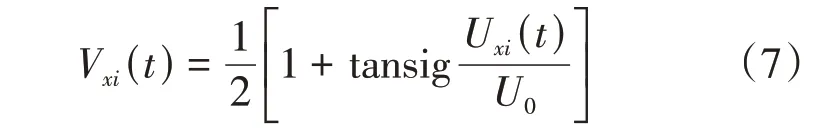
4）利用式（1）计算能量函数E；5）判断是否达到最大迭代次数k，如果t大于k，则输出能量函数值、路径、距离，否则t=t+1，转步骤2）。

3 仿真实验

3.1 TSP问题

算法用Python编程实现，为验证算法的有效性，用多个TSP问题的测试数据集进行实验。首先以10城市问题对算法进行测试，坐标数据见表1。

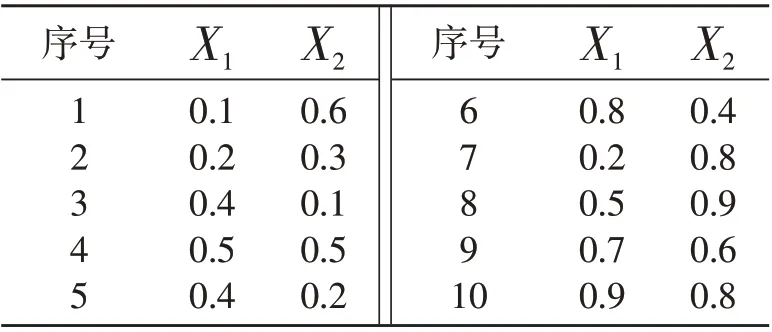
表1 10城市问题坐标数据

参数设置如下：U0取0.01～03，σ取-2～2，对Hopfield神经网络性能影响较大的参数A和D，根据事先用Hopfield神经网络计算结果确定大致范围，然后用差分进化算法进行最优参数的搜索，确定A∈（10,1200）,D∈（0,800）。在差分进化算法种群初始化时，在上述参数范围内用随机数产生个体，种群大小P为20，有4个参数需要优化，即编码长度n为4，交叉概率Pc为0.4，每个个体计算适应度时，k为150，返回计算得到的最低能量值作为适应度值，K为60。通过多次仿真实验，算法均能搜索到最优参数，根据最优参数，Hopfield网络求解到最优路径，结果如图2所示。

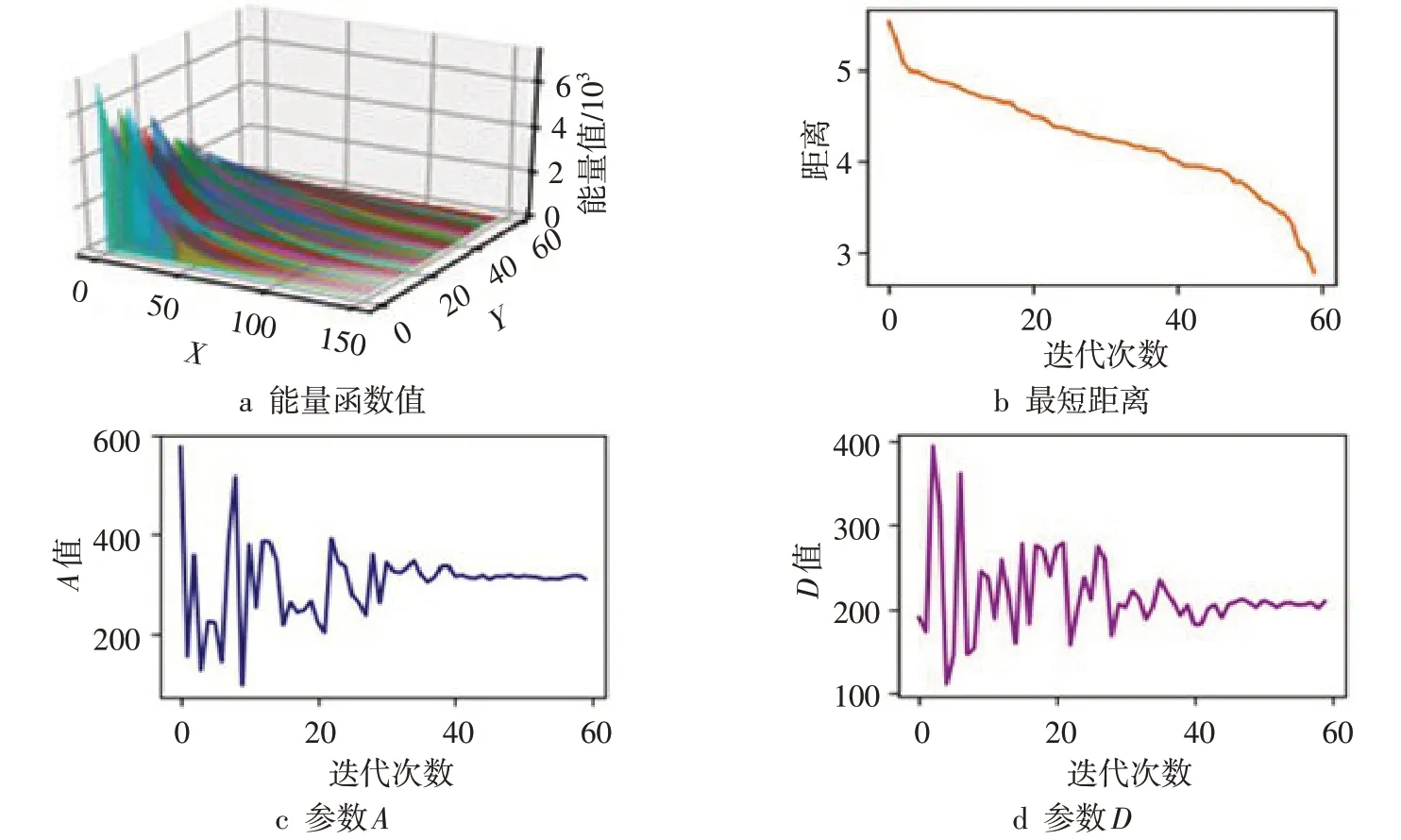
图2 能量函数值、最短距离和参数变化图

图2a为各代最优个体所对应的Hopfield网络计算的能量函数值变化情况，可以看出：算法初始迭代时，差分进化算法尚未找到合适的参数，Hopfield网络能量值比较慢的下降或者不能收敛；而在差分进化计算的末期、已找到合适参数时，网络能量能很快下降并稳定下来，这时网络能有效地求出最短距离。图2b为各代最短距离变化曲线，可以看出：所求最短距离呈单调下降，算法初始时，Hopfield网络难以收敛，从而不能有效地求解；而在末期，搜索到合适参数的情况下，Hopfield网络很快收敛，能较快地达到稳定状态，求出最短距离。图2c～d为参数A和D的变化情况，从各代最优个体编码中解析得到，可以看出：在差分进化计算后期，参数值基本处于稳定，表明算法找到了针对优化问题的最佳参数。根据搜索到的最佳参数，用Hopfield网络求解10城市问题的结果如图3所示。图3b为网络优化计算后得到的最短路径图，可以看出，网络迭代计算达到稳态后求得最短路径。图3c为网络能量函数值收敛曲线，只需经过400多次迭代，输出能量即可达到稳定状态。

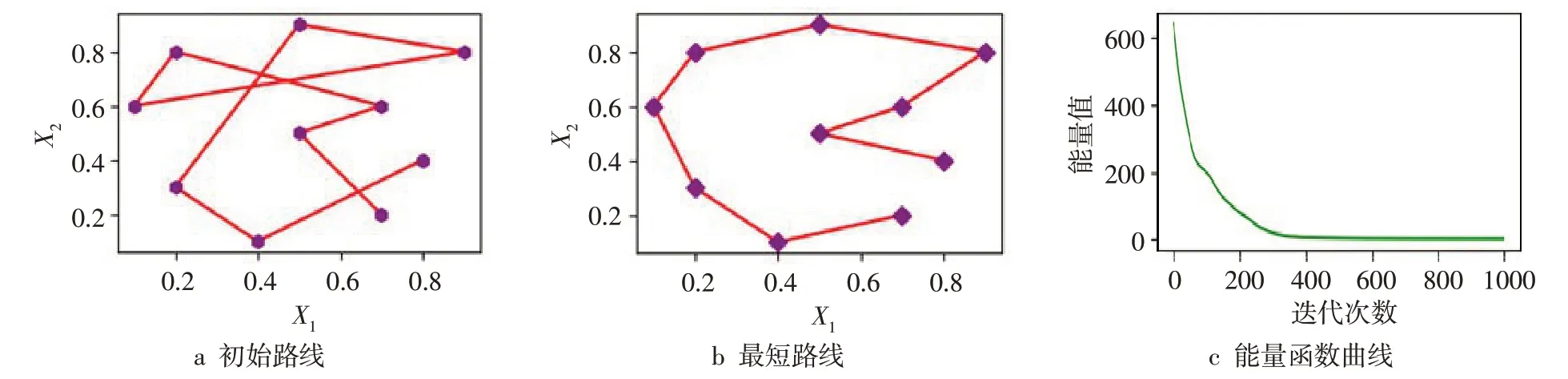
图3 用最优参数求解10城市问题结果

为检验算法求解较为复杂的TSP问题的性能，从TSPLIB测 试 库 中 选 择 了kroC100、ch150、a_gr666、pcb442、pr1002、pr2392城市规模较大的6个TSP问题实例进行测试，由于计算量和问题复杂性增加，为了确保算法能求解到较好的解，算法迭代次数和主要参数搜索范围适当取大一点，参数A,D∈( 0,120000)，P为100，k为800，K为2000，其他参数设置不变，进行10次仿真计算后求平均值，将算法所求解和实例的最优解进行对比，如表2所示。算法求解的结果如图4～5所示。从表2可以看出，文中算法所求解基本接近当前的最优解，表明算法在复杂TSP问题求解上效果良好。

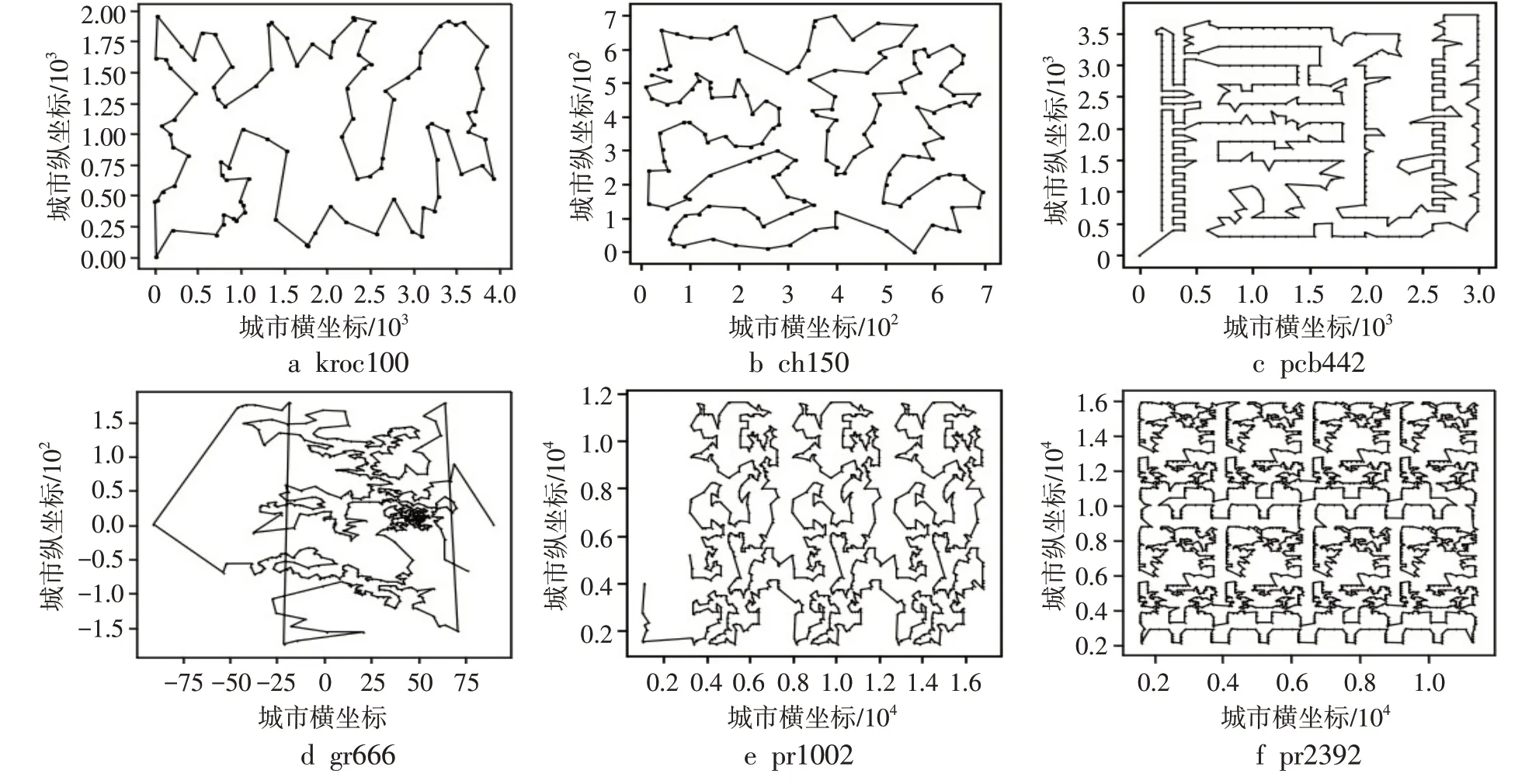
图4 TSP实例优化路径图

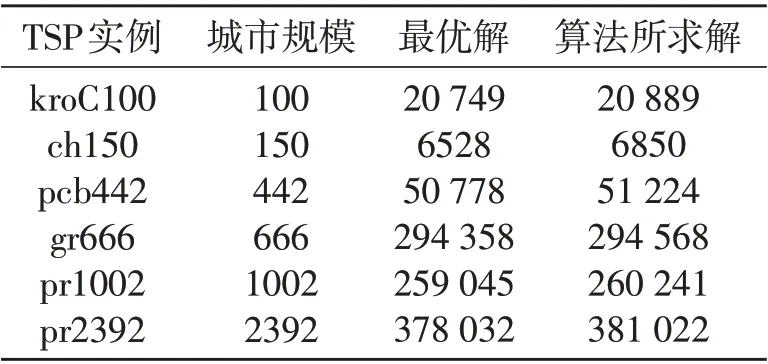
表2 TSP实例求解结果

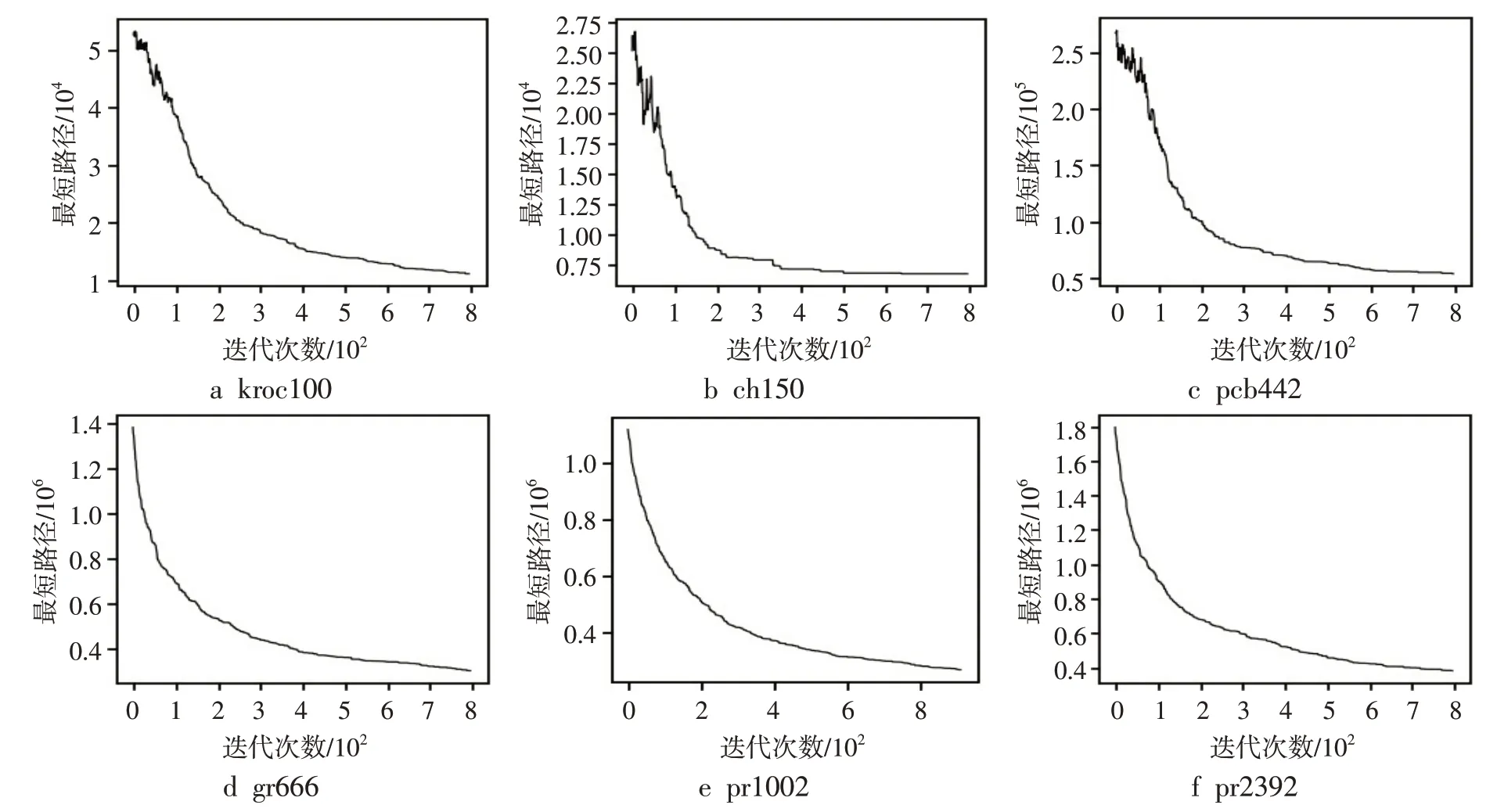
图5 算法在6个测试实例运行能量函数曲线

3.2 欺骗函数与等级函数问题

用4个典型的欺骗函数来测试算法的性能，其中每个输入变量的取值均为0或1，u为输入变量中1的个数，函数如下：

1）goldberg三阶欺骗函数

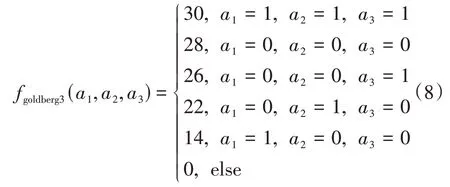
2）deceptive三阶欺骗函数

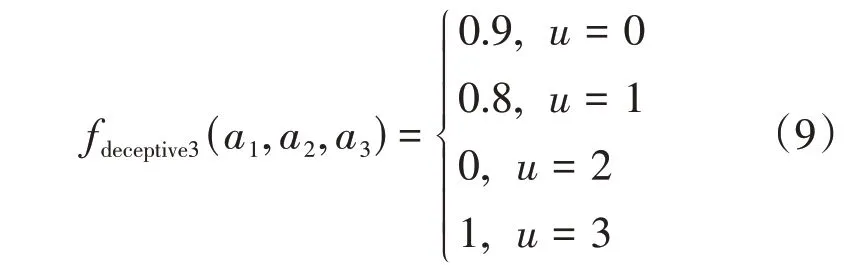
3）trap5五阶陷阱函数

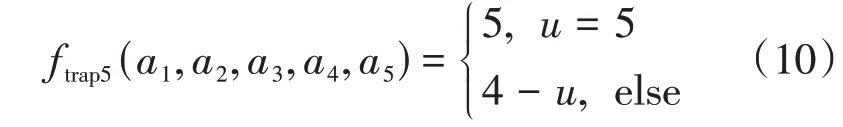
4）bipolar六阶双极欺骗函数

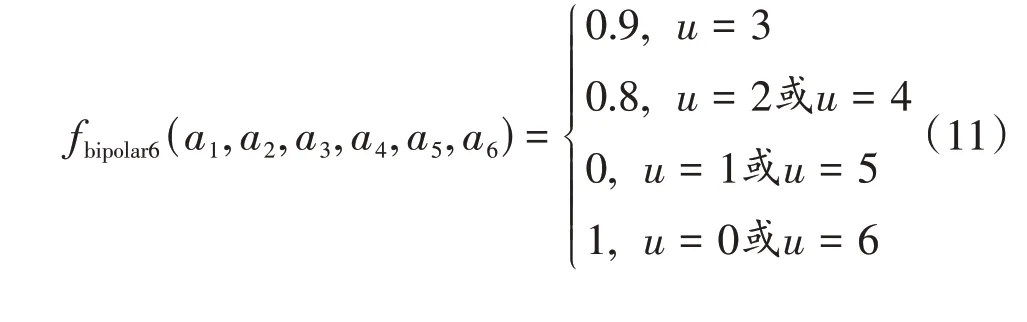
按如下连接方式构成大规模欺骗函数：

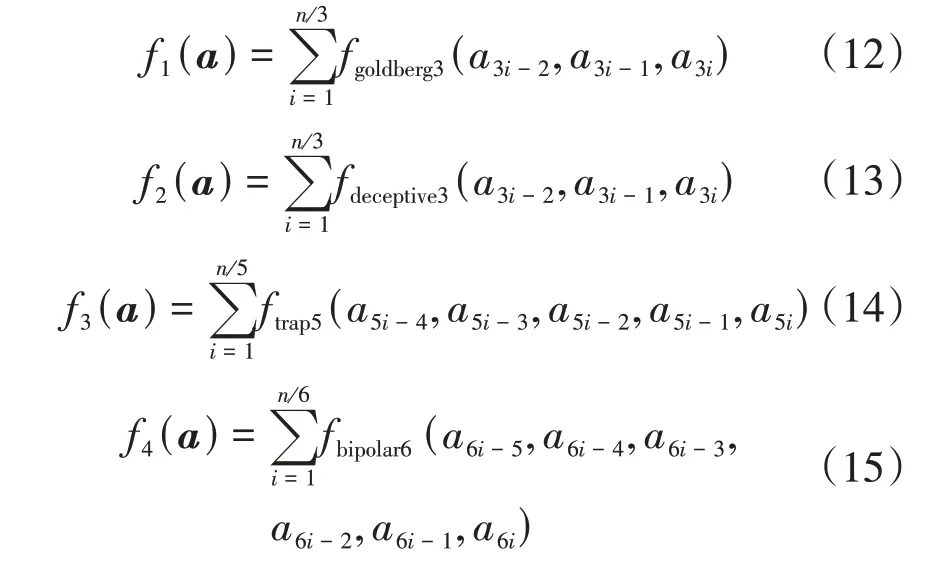
对goldberg、deceptive和bipolar函数，取变量长度为60，最优解为全1或全0，函数极大值分别为600、20、10；对trap5函数，取变量长度为100，最优解为全1，函数极大值为100。Hopfield网络和差分进化算法的主要参数设置和前述TSP问题的实验参数相当，对goldberg和trap5函数分别求解，求解过程中能量函数值、函数极大值、最优参数变化如图6～7所示。从图6c～d和图7c～d来看，在差分进化末期，参数值趋于稳定，算法搜索到了最优参数，同时也表明求解不同的函数，网络的最佳参数也不一样。从图6a和图7a可以看出，在算法初期、参数不合理的情况下，Hopfield网络基本不会收敛，求不出函数最优值，随着进化计算的进行，当搜索到最佳参数时，网络能比较稳定地收敛，快速求解出函数最优解。图6b和图7b显示的是，进化计算终止后，Hopfield网络以最优参数计算得到的收敛曲线，可以看出网络能稳定收敛。

图6 求解goldberg函数

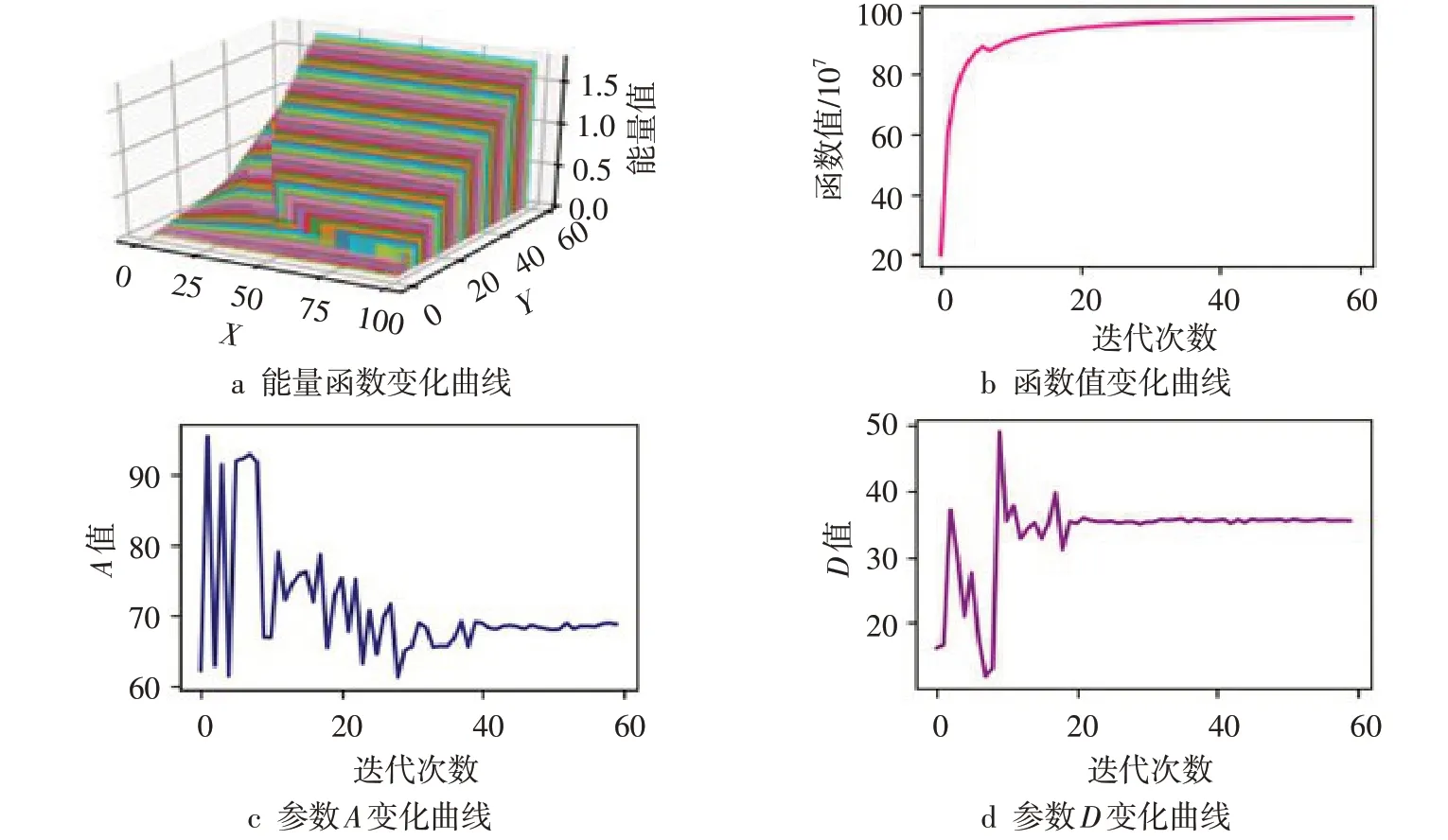
图7 求解trap5函数

选取等级函数HIFF和HtrapI进行实验，输入变量作为最底层，按映射函数将下层映射到上层，构成树状结构，每层的函数值之和即最终函数值。

HIFF函数的映射函数将下层的2个变量映射为上层1个变量，问题规模n为2level，映射函数为

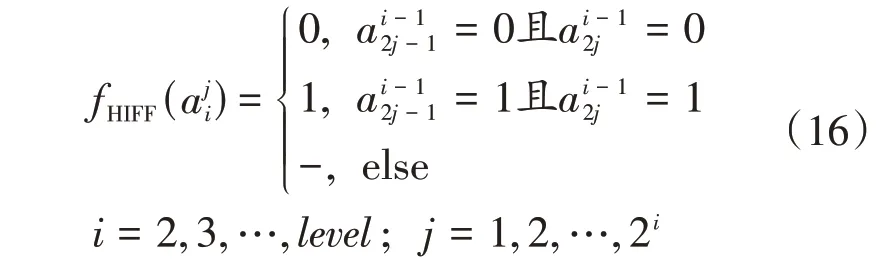
式中：level为层数。每层的函数值为

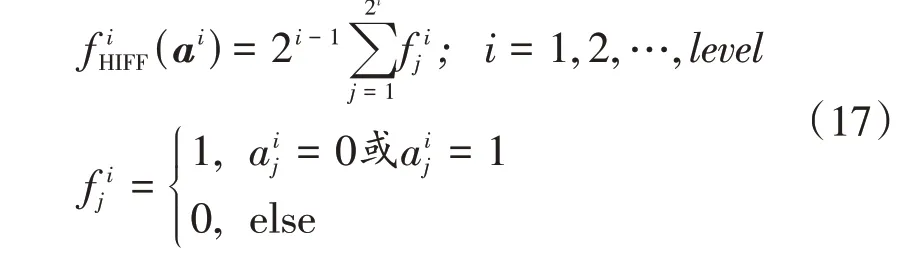
总函数值为

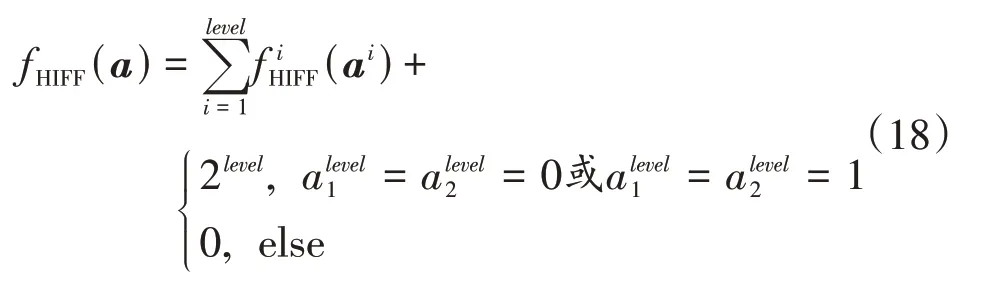
HtrapI函数和HIFF函数映射过程类似，将下层的3个变量映射为上层的1个变量，问题规模n为3level。映射函数为

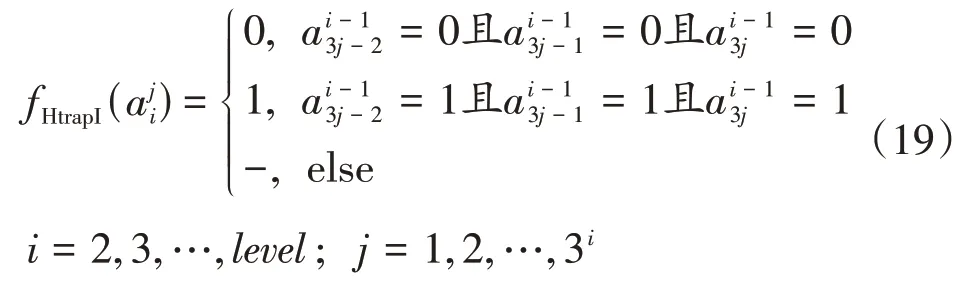
各层的函数值为

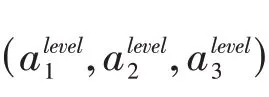
为比较优化性能，引入其他3个性能较好的优化算法进行对比，分别为差分进化算法（DE）、模拟退火算法（SA）和量子进化算法（QEA），文中算法记为DE-Hopfield。对goldberg函数，取n为60、90、120、150进行实验；对trap5函数，取n为50、100、150、200进行实验；对HIFF函数，取n为25、26、27进行实验；对HtrapI函数，取n为33、34、35进行实验。n取不同值时每种算法分别运行10次，并将结果计算平均值，具体运行结果如表3所示。

4 结语

针对Hopfield网络在求解优化问题时对参数过于敏感的问题，提出了用差分进化算法搜索最优参数的方法。文中方法在求解时，对于具体的优化问题，通过差分进化算法的优化计算，寻找到适合此问题的最佳参数，以优化问题和适合此问题的参数构造的Hopfield网络进行优化计算，从而快速、准确地解决各种优化问题。差分进化算法在连续值优化上有良好的效果，利用差分向量更新个体来寻求新的解，能更好地进行全局搜索，再通过优胜劣汰的选择机制保证了种群中的个体逐步朝最优解方向进化，通过上述算子的联合作用，网络参数得到优化。通过对TSP问题和欺骗函数问题这类组合优化问题的实验表明，文中方法提高了求解的稳定性，有效避免了Hopfield网络在给定参数不合适时不收敛的情况。对于超大规模的组合优化问题，随着问题复杂性增加，计算量会成倍增加，Hopfield网络的寻优效果也会变得越来越差，如何对参数搜索范围动态缩小、减小计算量、提高优化效果，是后续研究方向。