基于改进MAXBAND模型的城市绿波协调控制策略

毛源，向郑涛，陈宇峰

（湖北汽车工业学院 电气与信息工程学院，湖北 十堰 442002）

据公安部交通管理局统计数据显示，截至2021年3月，全国机动车保有量高达3.78 亿辆，其中72个城市汽车保有量超过100万辆。随着汽车保有量的大幅增加，城市交通堵塞状况变得愈发严重。通过不同的交通控制方法，可以缓解交通堵塞问题。城市绿波协调控制作为其中一种交通控制方法，广泛应用于城市交通信号控制，在缓解交通堵塞和提高道路通行效率方面发挥着重要作用。城市绿波协调控制主要采用2种方法：最小延误法和最大绿波带法［1］，相较于最小延误法，最大绿波带法可更直观地通过绿波带带宽反映出协调控制优劣，且需要条件少，应用较广泛。目前国内外对城市绿波协调控制开展较多研究，Little［2-3］等人提出了求解最大带宽的经典混合整数线性规划模型，并在日后加以改进，建立经典MAXBAND模型，可从周期时长、相序、相位差和绿波速度进行优化，使绿波带宽达到最大。Messer［4］等人利用半整数算法，提出了包含左转相位的绿波带带宽优化方法。Chang［5］等人从多条干路的路网考虑，提出MAXBAND-86协 调 控 制 模 型。Ganrtner［6］等 人 克 服MAXBAND模型中同一带宽问题，建立多带宽协调控制模型MULTIBAND，满足了不同路段的不同带宽的需求。Lu［7］等人将Robertson交通流离散模型引入到MAXBAND模型中，使其适应更复杂的交通情况。唐克双［8］等人提出了MULTIBAND干线协调模型，通过取消绿波带的中心对称约束、增加绿波带位置的约束提高绿波带带宽。于德新［9］等人通过取消绿波带对称约束及增加带宽比例约束，优化绿波带形式，同时引入红灯排队消散模型，建立改进的MULTIBAND模型。李祥尘［10］等人通过调整交叉口相位顺序和组成，提升了绿波协调控制的效果，不仅能增加干线双向绿波带的带宽，还能提升绿波速度对干线设计速度的适应性。张驰［11］结合NEMA相位和图解法，对相位相序进行调整，提高双向绿波控制中绿波带带宽。潘婷［1］等人考虑速度波动区间，设计求解绿波速度上限及下限，为驾驶者的车速调整提供了参考依据。但上述研究均存在一定不足：交通特性单一，将车辆速度固定，未考虑车队离散情况，相位相序考虑不足，交叉口在不同相位相序组合方式下，会呈现出不同的绿波带带宽。针对上述问题，对经典MAXBAND模型进行改进，在信号控制中引入双环相位，进行相位相序优化调整，并考虑车队行驶过程中存在的离散特性，进一步优化了相位相序，使绿波带宽达到最大化，同时也更加符合实际交通状况，获得较好的绿波协调控制效果。

1 MAXBAND模型优化

1.1 相位相序优化

当前交通信号控制领域主要采用2种相序方案：1）传统单环相位［12］，基本由4个相位组成，如图1所示，广泛应用于我国城市道路之中。由于单环相位存在对称性特点，在1个相位内至少为2股车流提供通行权，且无法调整，因此会造成某股车流的绿灯时长损失或不足的情况，进而影响交叉口通行能力。2）双环相位［13］，由美国电气制造协会提出，由8个相位组成，如图2所示。其中同环同段内2个相位的放行顺序及时长可任意调整，不会对其他相位产生影响，较好地避免了单环相位中存在的问题，同时在城市绿波协调控制中通过调整相位顺序及时长，实现绿波带宽最大化。双环相位相序4种组合方式如图3所示。

图1 单环相位

图2 双环相位

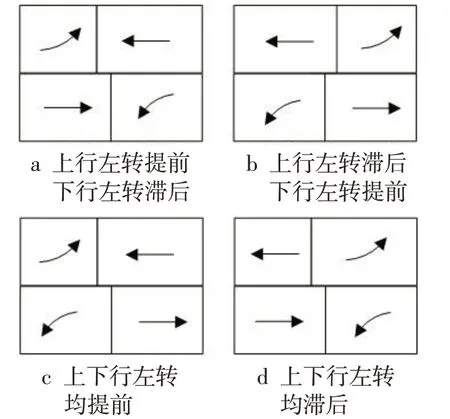
图3 双环相位相序方案

1.2 车队离散现象

城市道路上交叉口把连续的交通流分割成多股车队。车队从上游交叉口停车线驶出后，由于车辆运行条件、驾驶行为和自身特性等不同，导致车辆行驶速度存在差异，在到达下游交叉口停车线之前，逐渐拉开距离，发生车队离散现象，从而使车辆到达行程时间发生变化。对车队离散现象描述有2个经典模型，分别为Pacey模型和Robertson模型[14]。Pacey模型较适用于长距离路口，而在城市道路中交叉路口多为中短距离路口，Robertson模型更适用于城市绿波协调控制。因此采用Robertson模型描述车队离散现象。Robertson模型假设上下游交叉口断面之间的车辆行程时间服从移位几何分布，不同车辆的行程速度之间的差异通过车队离散系数来反映。即

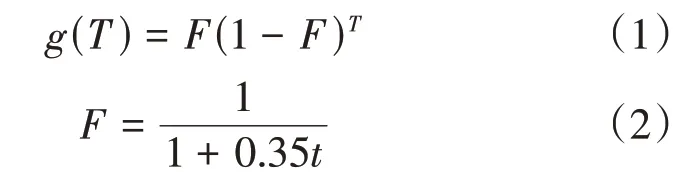
式中：g（T）为相邻交叉口间行程时间为T的车辆概率分布函数；T为车辆行程时间；F为车流离散系数；t为车辆最快的行驶时间。

1.3 改进模型

根据上述讨论，在MAXBAND模型的基础上采用双环相位进行相位相序调整，同时考虑城市道路中车队离散现象，结合Robertson模型，得到改进的MAXBAND模型：

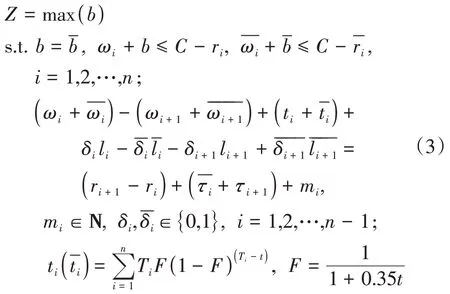
2 实验仿真分析

以某条由4个交叉口组成的城市道路为研究对象，仿真数据来源于文献［9］，交叉口1到交叉口4为上行方向，交叉口4到交叉口1为下行方向，4个交叉口的南北方向均为双向八车道，东西方向交叉口1、4为双向四车道，东西方向交叉口2、3为双向六车道。交叉口间距沿上行方向分别为566m、654m、720m，4个交叉口的小时交通流量如图4所示，其中实虚线箭头分别表示有无车流量进入，括号内数字从左至右分别对应进口道左转、直行和右转的流量。

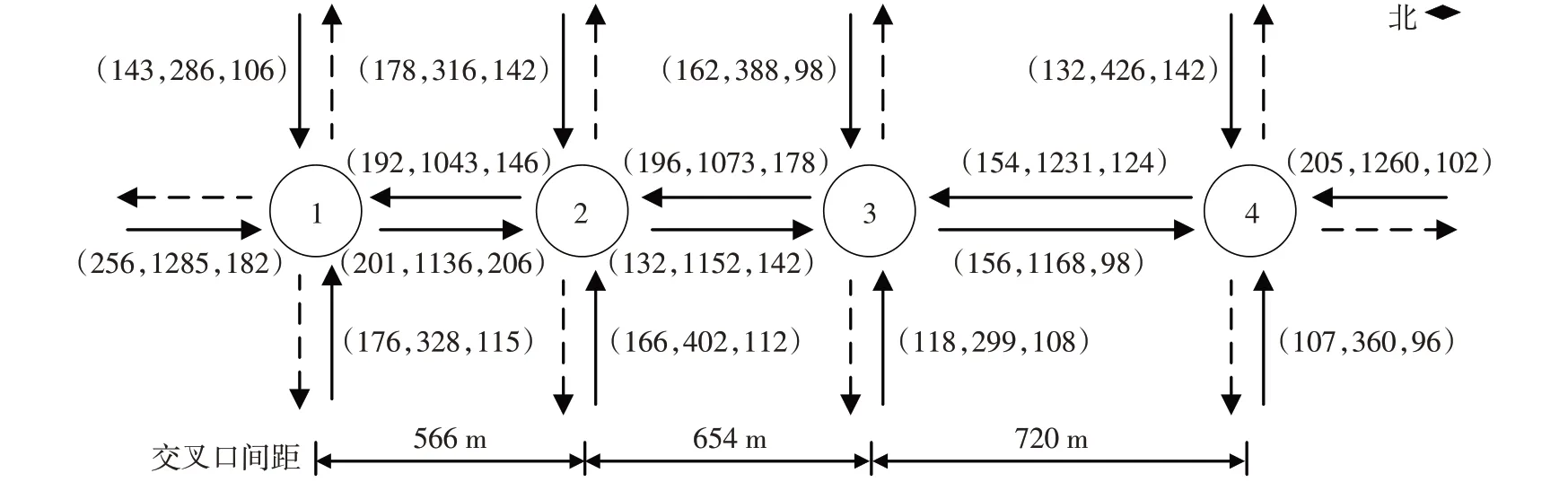
图4 仿真数据示意图

根据调查流量及车道分布情况，利用Webster模型［15］计算出各交叉口单环相位下的最佳信号周期及绿灯时长分配方案，计算结果如表1所示。其中交叉口1的信号周期时间最长，为145s，因此确定交叉口1为关键交叉口，将其他交叉口的周期时间调整为145s。在各交叉口单环相位信号配时方案基础上，采用双环相位对各个交叉口相位及绿灯时长进行调整，通过有效绿灯时长及绿信比的计算，得出双环相位下各交叉口的配时方案，如表2所示。南北方向信号设置存在相位搭接情况，相位相序的4种基本结构如图3所示。

表1 交叉口单环各相位信号配时 s

表2 交叉口双环各相位信号配时 s

根据改进模型以及交叉口数据，采用最优化求解工具Lingo进行求解［16］，求解结果如表3所示。各交叉口间相对相位差由各参数求解结果计算得出。相邻交叉口相位差计算公式为

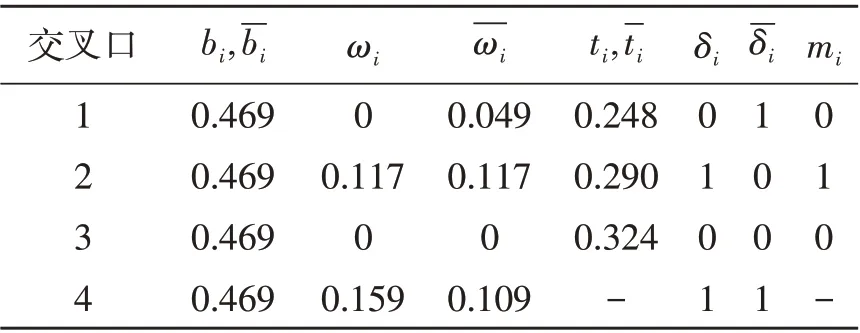
表3 改进的MAXBAND模型求解结果

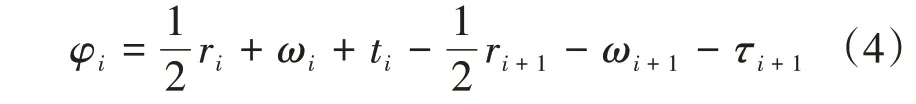
经计算可知，各交叉口间的相对相位差分别为17s、57s、22s。为便于仿真，采用绝对相位差，以交叉口1为基准交叉口，设定相位差为0，求得交叉口2～4的绝对相位差分别为17s、74s、96s。

选用Vissim交通仿真软件对优化后模型的有效性与实用性进行验证，以车辆平均旅行时间、延误、排队长度及停车次数作为主要指标进行分析。仿真时长为3600s，因仿真初期交通量逐渐增加，数据不具代表性，故分析指标数据选取600～3600s的数据，以10min的时间间隔输出评价参数。为防止单次仿真造成的随机性，采用10个随机数种子进行10次仿真，对仿真结果求其平均值。将改进模型与MAXBAND模型进行仿真结果对比，如图5所示。与经典MAXBAND模型相比，改进模型在交通信号中引入双环相位，通过Lingo求解结果，对相位相序进行相应调整，提高了绿灯时长的利用率，也进一步提升了绿波带宽；同时优化了车辆在路口间的行程时间，使之更加契合实际道路运行情况。改进模型在平均旅行时间、延误、排队长度及停车次数指标上均有较好效果，其中平均旅行时间减少了9.73%，平均延误时间减少了33.66%，平均排队长度减少了50.09%，平均停车次数减少了26.54%，整体绿波协调控制效果得到有效提升。

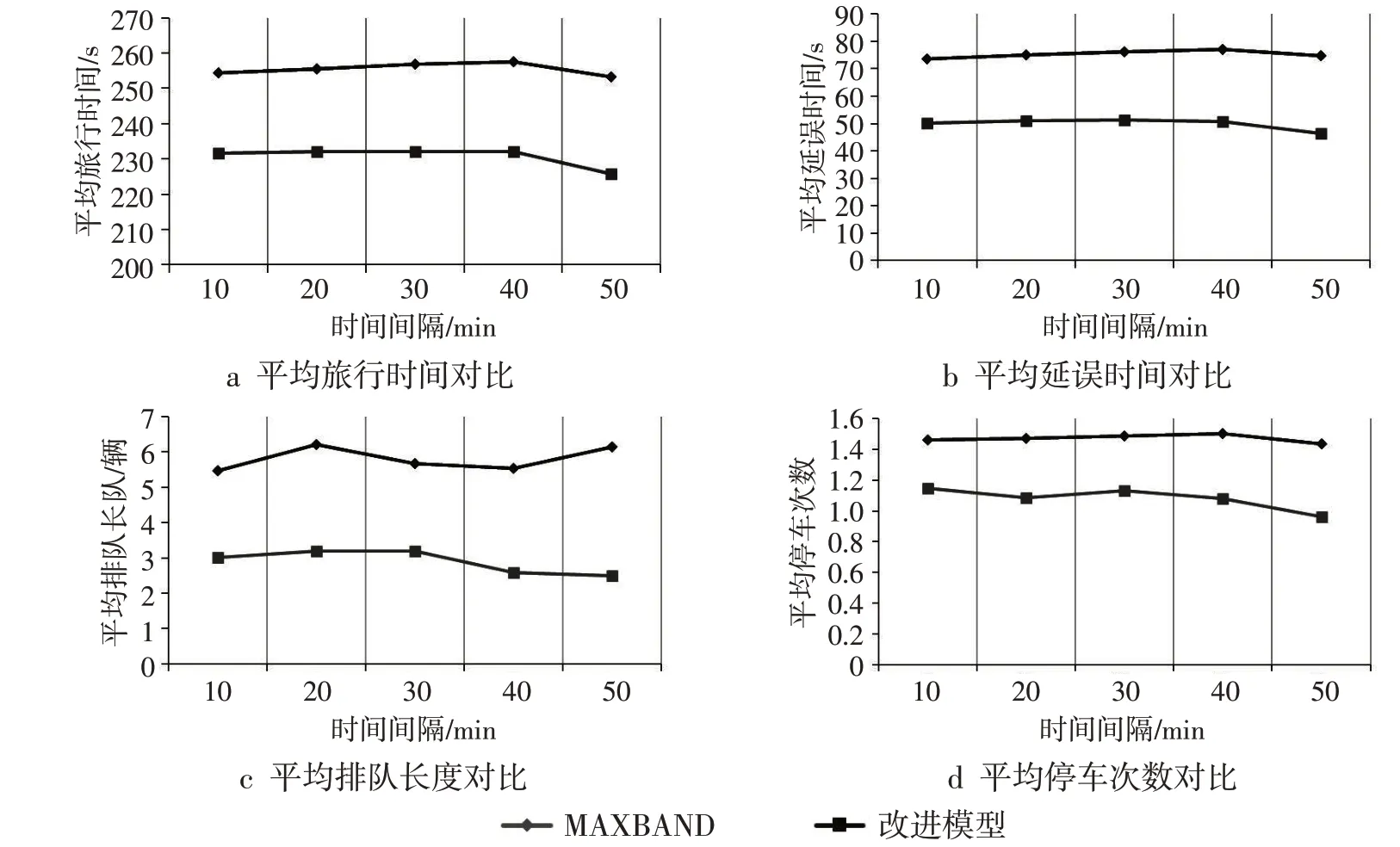
图5 仿真结果分析图

3 结论

通过分析城市绿波协调控制方法中存在的局限性，考虑了交通信号相位相序的调整，对车辆在行驶过程中存在的车队离散现象进行优化，提出改进的MAXBAND模型方案。实验仿真结果表明改进方案具有一定的有效性以及实用性，提升了城市道路整体通行效益。但在优化过程中未考虑排队清空时间动态变化带来的影响，难免有所偏差，后续研究中将考虑更多影响因素，设计出更适用于实际交通状况的城市绿波协调控制系统。