高速动车组撒砂装置振动疲劳寿命预测研究
2022-01-11赵子豪邹洪伟鞠增业刘元君
赵子豪,邹洪伟,鞠增业,刘元君
(中车青岛四方机车车辆股份有限公司,山东青岛266111)
高速动车组在运营服役过程中,撒砂装置作为车下安装部件,受到的随机振动激励是引发其失效破坏的主要原因。针对撒砂装置的振动特性,文献[2]对比了现车安装和试验室安装情况下的振动特性,发现边界条件对于撒砂装置的振动特性影响很大,进而可以影响随机振动耐久性试验的结果;文献[3]对撒砂装置及构架端部进行长期跟踪测试,发现等效应力幅值出现大幅波动与运行线路有关,并在时域及频域内分析了导致结构振动及应力水平过高的主要原因。本文基于目前的研究,将对撒砂装置进行模态试验,以校正撒砂装置的有限元模型并获得对应模态的阻尼比,依据IEC 61373:2010[4]进行随机振动及振动疲劳分析,以期形成高速动车组撒砂装置随机振动疲劳寿命预测方法。
1 IEC 61373:2010中对车辆安装设备的振动试验要求
IEC 61373:2010规定了对要安装在轨道机车车辆上的设备进行随机振动和冲击试验的要求,用于验证被试设备在铁路机车车辆正常环境条件下承受振动的能力。采用加速振动应力的方式来进行长寿命试验,通过每个轴向5 h的振动试验来等效25年的正常运行振动疲劳损伤。撒砂装置安装在车轴上,在其长寿命试验中采用3类车轴安装的ASD频谱。图1为随机振动ASD频谱密度,其中X为ASD频谱密度的标称值,f2为上限频率。撒砂装置的质量小于50 kg,因此f2取500 Hz,根据图1分别计算出垂向、横向、纵向的ASD频谱密度,具体数据如表1所示。
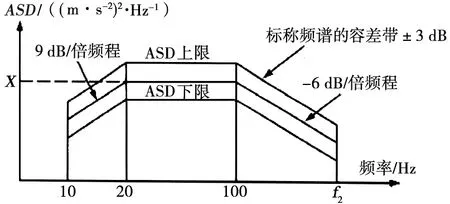
图1 3类车轴安装ASD频谱密度曲线

表1 车轴安装随机振动试验参数
2 模态试验与模态仿真
撒砂装置安装在轴箱体下方,通过4个螺栓固定在轴箱体上,由安装臂、排障板托架、管线等组成,如图2所示。
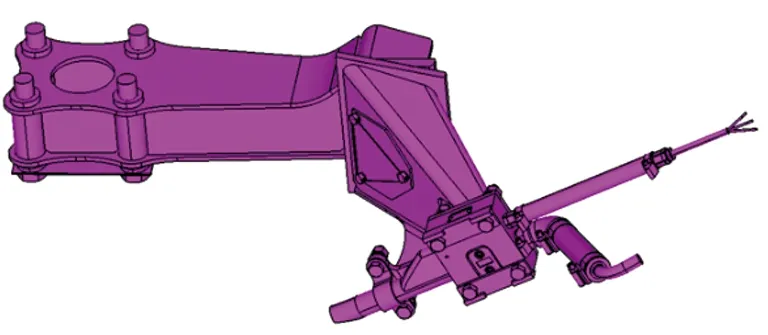
图2 某型动车组撒砂装置示意图
考虑在试验室无法完全实现现车安装情况下的随机振动试验,对于垂向振动、横向振动、纵向振动试验分别采用图3所示的试件安装方式进行试验,传感器布置如图4所示。

图3 振动试件安装方式
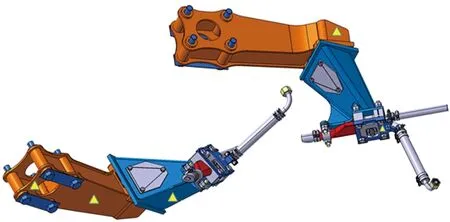
图4 传感器布置
2.1 模态试验
试件在垂向安装状态下,使用力锤对其进行敲击,通过加速度传感器将激励转换为电信号,经LMS数采装置把电信号转换为模态响应参数。模态参数利用幅频特性和相位共振原理进行辨识。在激振条件下,观测振动响应的幅值和相位,当满足幅值和相位共振条件时记录振动响应和频率信息,这时的激励频率就是撒砂装置对应振型的共振频率。振型根据撒砂装置响应的幅值和相位信息按模态辨识理论中的共振法确定。
表2为垂向模态试验测得的模型的频率数据,图5为试验得到的1阶模态振型。
综上所述,将控制血糖护理干预措施应用于子宫肌瘤合并糖尿病患者中效果显著,可确保患者血糖水平趋于平稳,并控制并发症发生几率,促进患者机体康复,临床应用价值较高,可大面积推广并应用。

表2 垂向模态试验数据
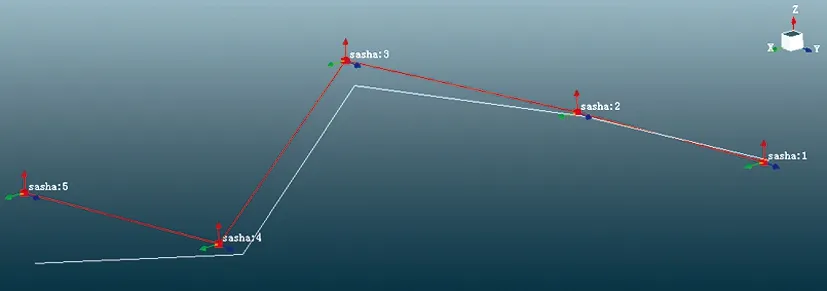
图5 垂向模态试验1阶振型
2.2 模态仿真与模态试验结果对比与分析
根据试验模型进行仿真建模,计算试件垂向安装状态下结构的模态并与模态试验结果进行对比。表3为在实施修改连接方式及网格类型等优化措施后,仿真模型的模态与试验模态数据对比,其中相对误差=|(仿真数据-试验数据)/试验数据|×100%。同时采用相同步骤获得试件横向和纵向安装状态下结构的试验频率及模态阻尼比。

表3 垂向仿真模态与试验模态数据对比
由于安装在振动台上的撒砂装置是个完整的装配体,涉及多个部件之间的螺栓连接,而螺栓连接造成了机械系统的非连续性,会引入额外的能量耗散,连接接触阻尼占到了整体结构阻尼的90%,导致了整体刚度变化,从而直接影响系统的固有频率和动力学特性[5]。螺栓连接的作用机理极其复杂,具有较强的非线性特性,而动力学仿真基于线性分析假设,本身不能考虑非线性的影响,因此在计算原理上存在一定误差。
3 随机振动分析
随机振动分析方法分为时域法和频域法。因时域法不适用于长时间随机激励工况,而且IEC 61373:2010规定的是ASD频谱,所以本文使用频域法进行随机振动分析。
频域随机振动基于如下动力学方程:
f(s)=(Ms2+Cs+K)u(s)
(1)
式中:f(s)——基于复频率的外载荷函数;
M——质量矩阵;
C——阻尼矩阵;
K——刚度矩阵;
u(s)——基于复频率的模态振型函数;
s——复频率。
令H(s)=(Ms2+Cs+K)-1,得到:
u(s)=H(s)f(s)
(2)
式中:H(s)——结构的频响函数。
式(2)两边乘以其转置共轭项,得到:
u(s)u(s)*=H(s)f(s)f(s)*H(s)*
(4)
记为:
Suu*(s)=H(s)Sff*(s)H*(s)
(5)
式中:Suu*(s)——输出的互功率谱矩阵;
Sff*(s)——输入的互功率谱矩阵。
在M、C、K一定的情况下,就能得到结构的振动响应。
使用OptiStruct软件对撒砂装置进行3个方向上的随机振动分析。阻尼采用试验值,先进行基于预应力的频响分析,得到结构的频响函数H(s),再进行随机振动工况分析。认为振动台对于结构的激励幅值相位一致,Sff*(s)简化为自功率谱加载,分析中载荷谱使用图1的ASD频谱密度曲线,求解得到撒砂装置的随机振动响应。图6、图7、图8分别为得到的垂向、横向及纵向的RMS应力,最大值分别为40.8 MPa、34.3 MPa、26.4 MPa。

图6 垂向振动RMS应力
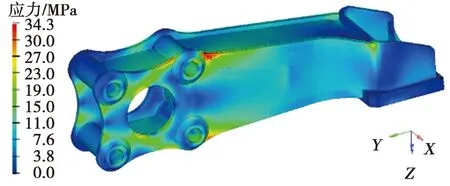
图7 横向振动RMS应力
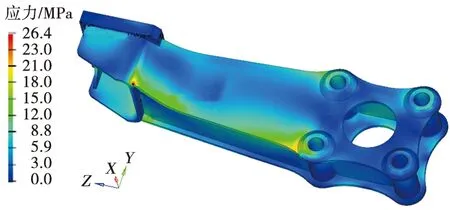
图8 纵向振动RMS应力
4 振动疲劳分析
Dirlik雨流幅值分布公式是一种经验公式[6],适用于窄带和宽带的计算,是随机振动疲劳分析采用的普遍方法,Dirlik概率密度函数p(σ)可表达为:
(6)
其中:
D3=1-D1-D2
式中:σ——应力;
m0、m1、m2、m3、m4——功率谱密度函数的惯性矩。
基于Miner线性累积损伤理论使用HyperLife软件进行求解疲劳寿命,一般的随机振动疲劳分析软件基于频响分析的结果,再设置ASD频谱密度进行求解,HyperLife软件可以基于随机振动分析的结果进行疲劳寿命统计。
图9、图10、图11分别为垂向、横向、纵向的疲劳寿命云图。

图9 垂向振动疲劳寿命
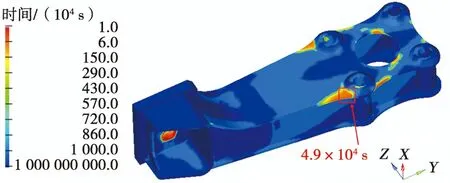
图10 横向振动疲劳寿命
从图9~图11可知,3个方向上的疲劳寿命分别为3.4×104s、4.9×104s和8.3×105s,换算成小时为9.4 h、 13.6 h和230.6 h,均大于IEC 61373:2010中规定的垂向、横向、纵向均为5 h的冲击试验结果,表明撒砂装置的设计能满足随机振动的使用要求。

图11 纵向振动疲劳寿命
5 结束语
本文研究了撒砂装置振动疲劳寿命预测的方法,通过模态试验得到系统的模态阻尼比并校核有限元模型,采用频域分析方法施加IEC 61373:2010中3类随机振动ASD频谱密度得到系统的RMS应力值,再采用Dirlik法和Miner损伤理论对结构疲劳寿命进行统计,最终得到各个方向上系统的疲劳寿命。
由于试验室安装状态与现场安装状态有一定的差别,而且试件3个方向的安装状态各不相同,计算结果中包含了工装对于结构的影响。撒砂装置作为一个装配体,各个部件通过螺栓连接,给系统带来了刚度和阻尼非线性的因素,如何更加合理处理螺栓连接是需要持续关注的动力学问题。
