基于深度可分离卷积和门控循环单元的轴承剩余寿命预测研究

赵志宏，李乐豪，杨绍普，李 晴

(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点试验室，河北 石家庄 050043；2.石家庄铁道大学 信息科学与技术学院，河北 石家庄 050043)

滚动轴承是机械设备中最常使用的零部件之一，对于机械设备的可靠性至关重要，滚动轴承的损坏轻则停机检修，重则危害乘客的生命安全，因此对其展开健康监测具有重要意义。在滚动轴承监测过程中，对轴承进行剩余寿命预测是实现预测性维护的重要途径[1]。

随着滚动轴承寿命研究的不断发展，寿命预测方法逐渐走向成熟，现有的预测方法有3种：基于失效机理的寿命预测、基于统计学的寿命预测和基于模型的寿命预测。基于模型的寿命预测中机器学习方法可以很好地针对不同退化趋势进行拟合，具有原理简单、专家经验依赖少、适用性较广等优点[2]；文献[3]利用支持向量机建立轴承寿命预测模型，较为准确地预测了滚动轴承的剩余寿命；文献[4]以方根均值为特征指标评估轴承的退化状态，并结合多变量支持向量机在小样本下实现了轴承剩余寿命预测；文献[5]使用多层感知机进行轴承剩余寿命预测，并与自回归移动平均方法进行对比，验证了多层感知机具有更好的预测效果。

2006年，文献[6]提出了深度学习理论，深度学习以其强大的函数拟合、特征提取能力推动了很多领域的发展，由于深度学习模型相较于传统的机器学习模型具有更深的网络结构和更强的非线性能力，越来越多的专家学者使用深度学习模型展开轴承剩余寿命的研究；文献[7]提出一种基于深度可分离卷积神经网络(depthwise separable convolutional，DSC)的轴承寿命预测方法，得到了优于其他深度学习方法的预测结果；文献[8]提出一种基于全卷积神经网络的轴承寿命预测方法，并使用加权平均方法对预测值进行降噪，提高了预测精度，获取了较为准确的轴承剩余寿命；文献[9]提出一种基于多尺度卷积神经网络的剩余寿命预测方法，提取轴承的多尺度退化特征信息，获取了较高的预测精度。

本文使用深度可分离卷积提取轴承振动信号中的空间特征信息，利用门控循环单元(gated recurrent unit，GRU)进一步提取振动信号中蕴含的时间特征信息，并通过全连接层进一步进行特征提取和输出健康指标(heath indicator，HI)，利用Savitzky-Golay滤波器对获取的健康指标进行降噪，然后将健康指标拟合为自变量为时间、因变量为已使用寿命的一次函数，较为准确地预测了轴承的剩余寿命。

1 理论介绍

1.1 深度可分离卷积

深度可分离卷积的结构如图1所示，主要由深度卷积和逐点卷积组成。传统卷积每个通道中卷积核的数量与输入的通道数一致，而深度卷积的一个通道只有一个卷积核，因而深度卷积可以大幅减小参数量和计算量；逐点卷积为一种卷积核大小为1×1的传统卷积，通过逐点卷积可以融合每个通道对应位置提取到的特征，避免关键特征只存在于一个通道中，并且可以通过合理设置通道数实现特征的升维和降维。

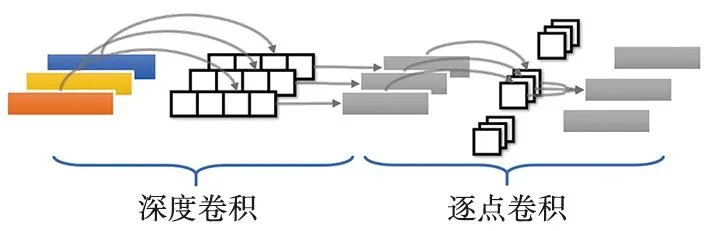
图1 深度可分离卷积结构

1.2 自注意力机制

自注意力机制(Self-attention)是Transformer神经网络的重要组成部分[10]，常用于自然语言处理。自注意力机制计算时，每一个特征都会和其他特征进行加权计算，可以注意到不同特征之间的关系，并根据特征与特征之间的相关程度决定所提取的特征。自注意力机制的计算流程如图2所示。

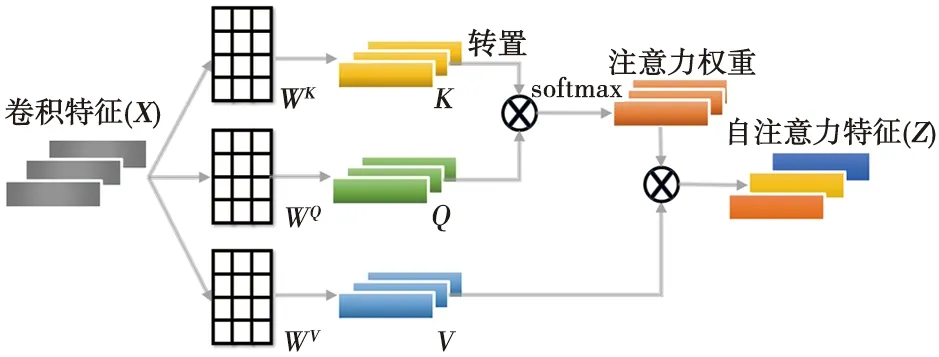
图2 自注意力机制的计算流程

自注意力机制所提取的特征Z可通过softmax将Q、K之间的相关程度转化为权重并乘以V获取：

(1)

Q=X⊗WQ

(2)

K=X⊗WK

(3)

V=X⊗WV

(4)

式中：dk——Q的维度；

X——输入数据；

Q、K、V——分别为X与WQ、WK、WV相乘后经过线性变换所提取到的特征；

Q⊗KT——Q、K之间的相关程度。

1.3 门控循环单元

GRU是一种长短期记忆神经网络(long short-term memory，LSTM)的变体，为门控循环单元，可以解决循环神经网络梯度消失、梯度爆炸问题，是一种可以较好地捕获时间序列中较远时间距离依赖关系的神经网络[11]。相较于LSTM，GRU单元3个门(遗忘门、输入门和更新门)减少到了2个门：重置门和更新门，重置门决定了如何将新的输入数据与前面GRU的状态信息相结合，更新门决定了前面的状态信息保存到当前时间GRU的量。GRU的结构如图3所示。

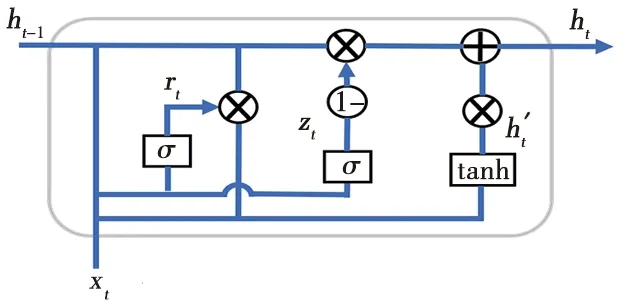
图3 GRU结构

当前GRU的状态信息，即GRU输出ht的计算方式为：

(5)

rt=σ(Wr⊗[ht-1,xt])

(6)

zt=σ(Wz⊗[ht-1,xt])

(7)

h't=tanh(Wh⊗[rt·ht-1,xt])

(8)

rt、zt——分别为重置门和更新门的输出；

Wr、Wz和Wh——权值矩阵；

xt——当前GRU的输入数据。

2 基于DSC-Attention-GRU的剩余寿命预测模型

为解决轴承寿命预测问题，本文提出一种基于深度可分离卷积和门控循环单元、结合自注意力机制的DSC-Attention-GRU模型。DSC-Attention-GRU模型的网络结构如图4所示，图4中，MaxPool为最大池化层(MaxPooling Layer)，Dense为全连接层，DSConv为深度可分离卷积。

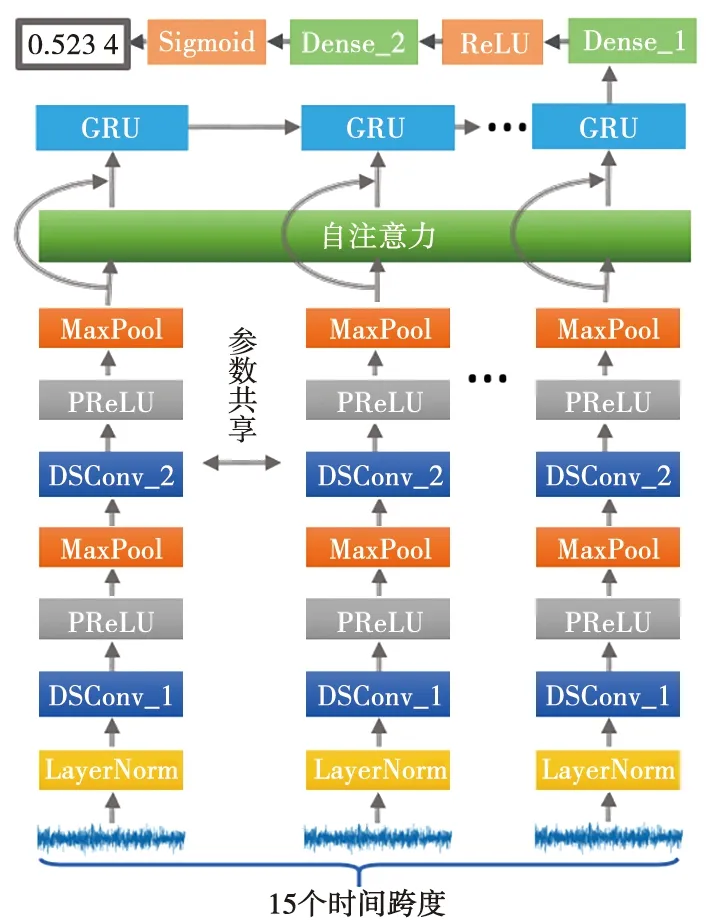
图4 DSC-Attention-GRU模型网格结构

首先使用LayerNorm对输入数据进行标准化[12]，LayerNorm的计算方式为：

(9)

式中：x——输入数据；

E(x)——求均值函数；

Var(x)——求标准差函数；

γ、β——分别为权值和偏置，是通过训练确定的参数；

ε——极小的正数。

使用深度可分离卷积提取每个时间样本的空间特征，深度可分离卷积网络具有相同的参数，在深度可分离卷积层间使用PReLU激活函数增强模型的非线性能力，使用最大池化层缩减特征尺寸；使用Self-Attention关注对于轴承寿命预测有用的信息；使用残差连接将深度可分离卷积所提取的特征和自注意力层提取的特征融合；使用GRU提取特征间存在的时序信息，获取蕴含轴承剩余寿命信息的特征；最后使用全连接层进一步提取特征，输出剩余寿命。神经网络中的重要参数如表1所示。

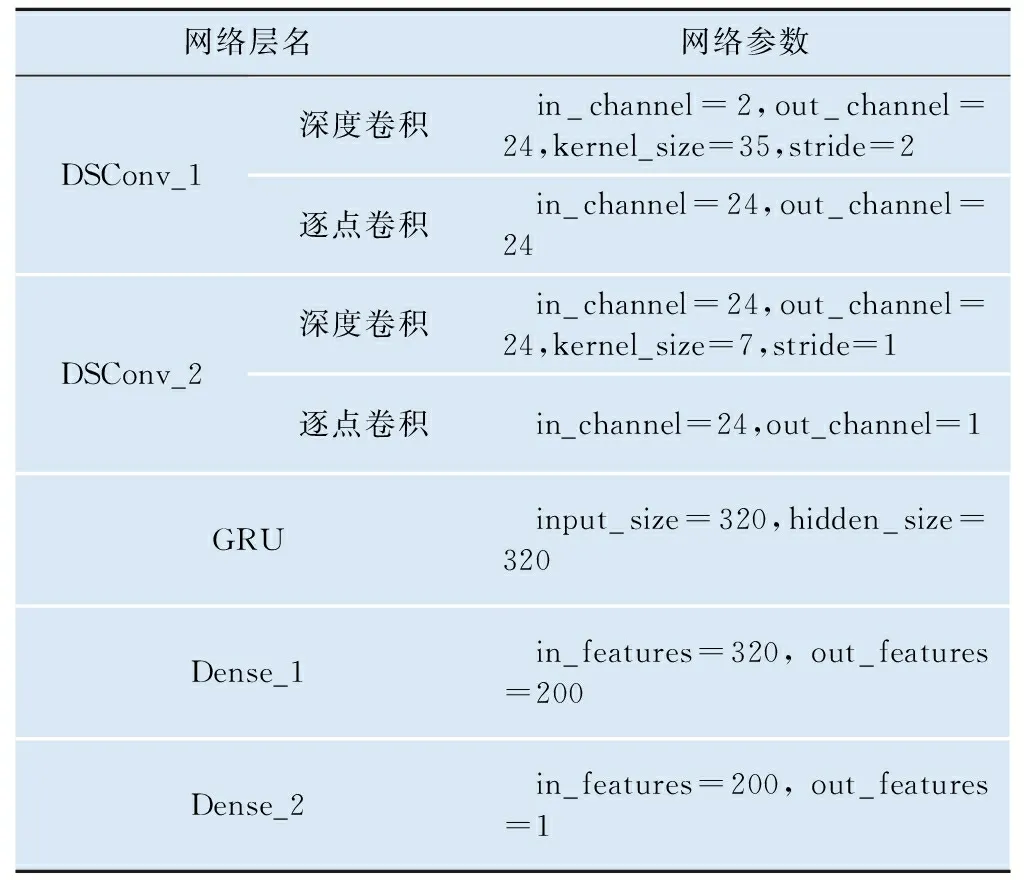
表1 网络参数

3 基于DSC-Attention-GRU的剩余寿命预测方法

基于DSC-Attention-GRU的剩余寿命预测流程如图5所示。可以分为训练阶段和测试阶段。

3.1 训练阶段步骤

(1) 第一步，构建DSC-Attention-GRU模型。

(2) 第二步，选择DSC-Attention-GRU模型中的卷积核数量、通道数、学习率等超参数。

(3) 第三步，将训练数据集中的每15段连续时间对应的水平和垂直方向的2个振动信号作为一个样本，并以轴承已使用寿命为样本制作标签，该标签为轴承实际的健康指标，具体计算方式为：

(10)

式中：HIj——第j个样本对应的健康指标；

m——样本个数。

使用训练数据迭代训练DSC-Attention-GRU模型，使用Adam优化器进行参数优化调整权重。

(4) 第四步，评估模型。如果损失收敛到设定的阈值，保存模型，进入测试阶段；否则返回第三步继续训练。

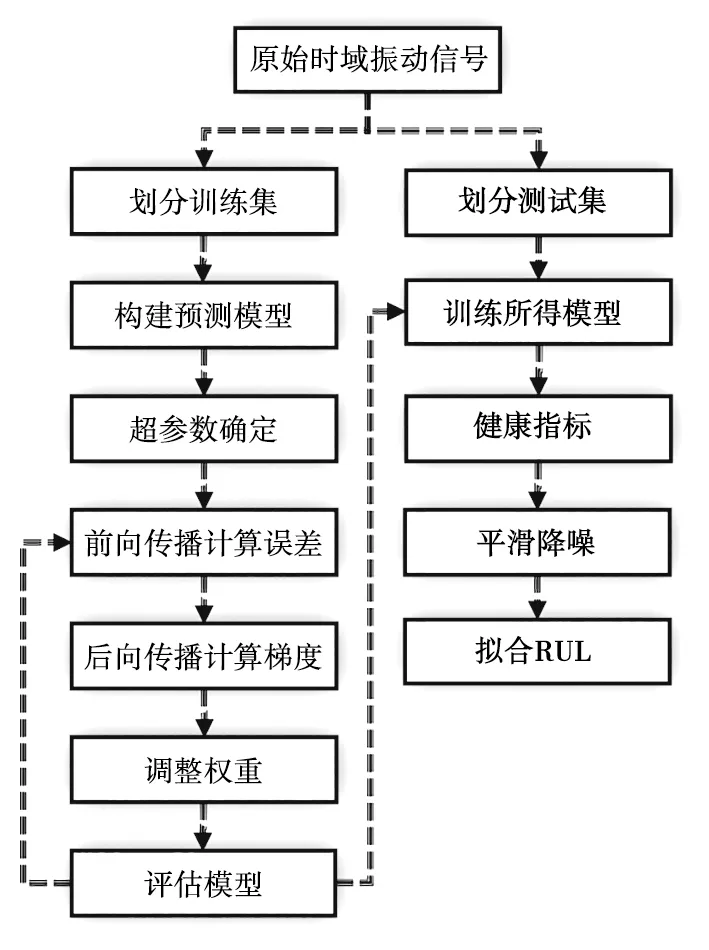
图5 剩余寿命预测流程

3.2 测试阶段步骤

(1) 第一步，将测试数据输入DSC-Attention-GRU模型得到健康指标；

(2) 第二步，使用Savitzky-Golay滤波器[13]对健康指标进行降噪；

(3) 第三步，对降噪后的健康指标进行一次函数拟合，拟合成时间为自变量，健康指标为因变量的一次函数。在一次函数下计算健康指标为1时对应的时间，该时间与当前时间的差值即为预测的剩余寿命。

4 寿命预测试验

4.1 试验数据

为验证本文所提方法在轴承剩余寿命预测中的有效性，使用PHM2012滚动轴承全寿命数据集[14]进行试验。采集数据的试验台主要由采集模块、调压器、压力传感器、加速度计、交流电机、测试轴承等组成(图6)。

图6 数据采集试验台

测试轴承的型号为6804DU，试验时对轴承施加径向负载以加速轴承损坏，每隔10 s采集0.1 s的水平和垂直方向的振动加速度信号，采样频率为25.6 kHz，加速度超过20g时停机。分别在3种工况下对17个轴承进行了试验，工况1的转速为1 800 r/min，负载为4 000 N；工况2的转速为1 650 r/min，负载为4 200 N；工况3的转速为1 500 r/min，负载为5 000 N。轴承与其数据组成如表2所示。

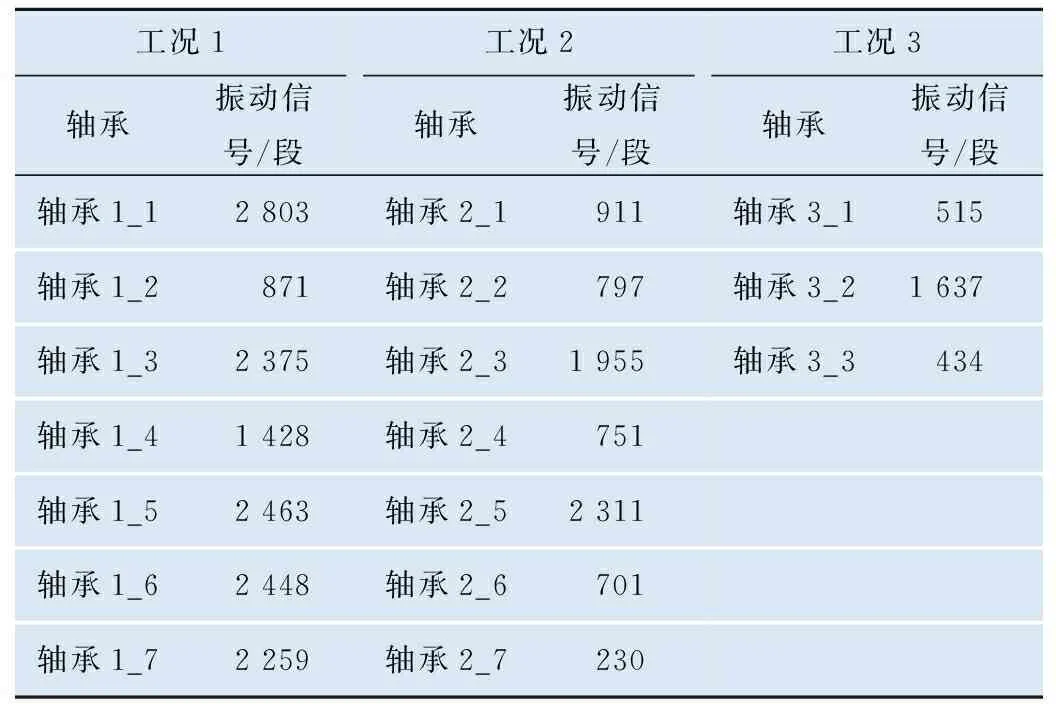
表2 试验数据

4.2 试验结果

为了充分训练模型以得到较好的预测结果，使用轴承1_3和轴承2_6作为测试集，其余轴承作为训练集。模型训练过程的损失曲线如图7所示。从图7可以看出，损失下降的速度较快，同时收敛的过程也较为稳定，没有出现大幅度的波动，最终损失函数收敛至0.002 81，表明对训练集的拟合情况较好。

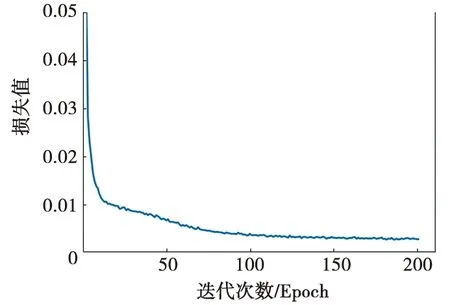
图7 损失曲线

在测试集轴承1_3和轴承2_6上获取的健康指标如图8所示，可以看到获取的健康指标曲线围绕实际的健康指标曲线上下波动，经过Savitzky-Golay滤波平滑后，整体曲线较为光滑，可以反映轴承从健康至完全失效的退化过程。降噪前后的单调性和趋势性的对比如表3所示，可以看到单调性显著增加；趋势性也略有增加，在轴承1_3上增加了0.006，在轴承2_6上增加了0.037。通过图8和表3可以看出，Savitzky-Golay滤波器降噪效果较好，可以有效改善健康指标的单调性和趋势性，更好地拟合轴承的退化过程。

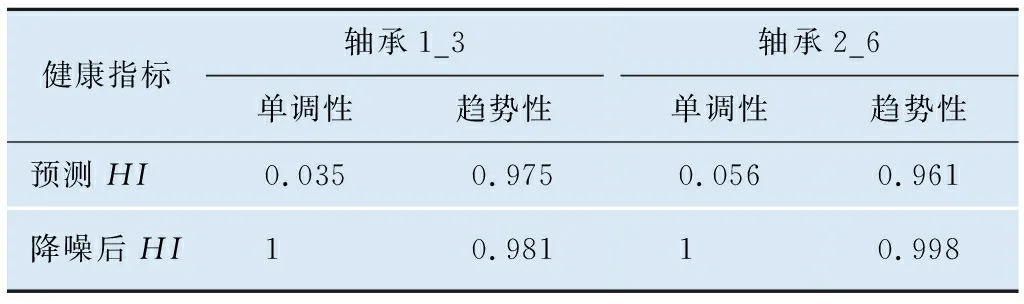
表3 降噪前后轴承健康指标单调性与趋势性对比

使用t-SNE降维可视化方法[15]对轴承2_6的全寿命数据经过GRU提取的特征进行可视化，可视化结果如图9所示。图9中由浅到深的点代表从初始时刻到完全损坏时刻的样本，可以看到不同阶段的样本排列有序，反映出DSC-Attention-GRU模型可以有效提取轴承的退化特征。

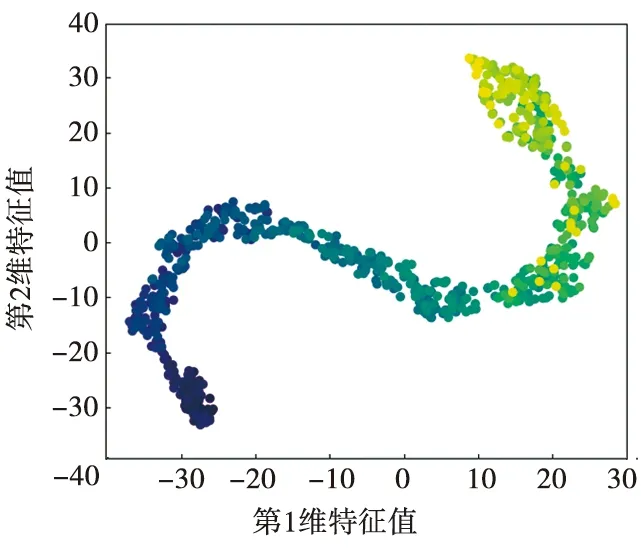
图9 t-SNE降维可视化结果

在实时获取健康指标后，将降噪后的健康指标拟合为一次函数，然后计算该一次函数增长至1所用的时间，使用误差百分比对预测效果进行评价，误差百分比Er的计算方式为：

(11)

式中：ActRUL——预测剩余寿命；

RUL——真实剩余寿命。

轴承1_3和轴承2_6在多个寿命阶段的剩余寿命预测结果如表4所示。从表4中可以看到，轴承1_3随着已使用寿命的增加，寿命预测效果逐渐改善，在已使用9 500 s和14 250 s时取得了较好的寿命预测效果，与真实剩余寿命的误差较小；轴承2_6在多个寿命阶段均都取得了较好的预测效果。

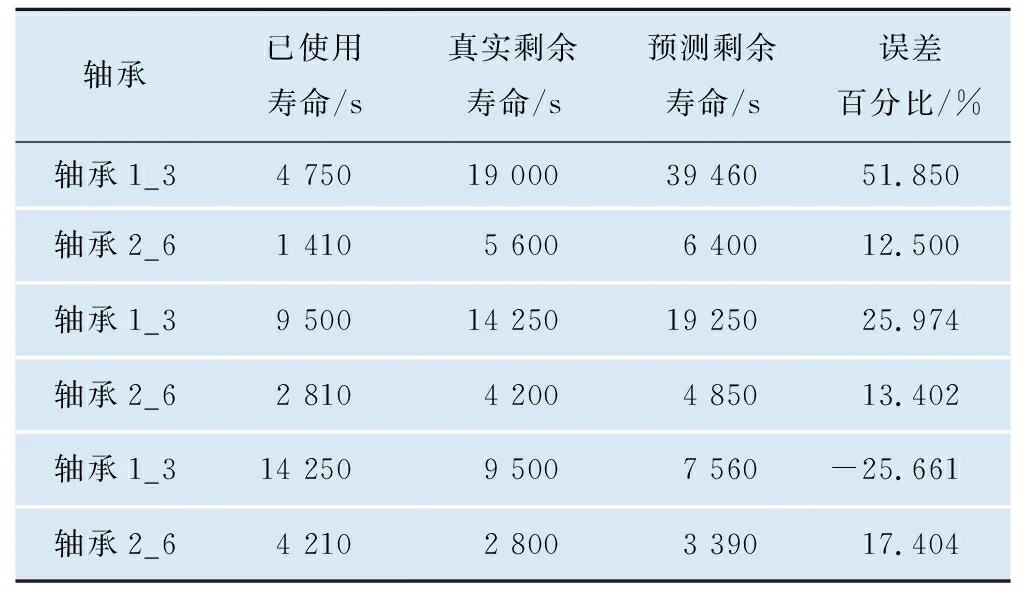
表4 剩余寿命预测结果

5 结束语

本文提出了一种使用自注意力机制的深度可分离卷积和门控循环单元的剩余寿命预测模型，使用Savitzky-Golay滤波器平滑健康指标，并结合一次函数拟合获取剩余寿命值，实现了轴承的剩余寿命预测。寿命预测试验结果表明：DSC-Attention-GRU模型可以较好地从振动信号中提取轴承的退化特征，可以有效拟合从振动信号到健康指标的映射关系。Savitzky-Golay滤波器对健康指标的平滑降噪效果较好，可以显著提升健康指标的单调性，通过一次线性拟合可以较好地预测剩余寿命。