基于WPD-ASTFT和SVM重载铁路钢轨波磨诊断方法
2022-01-11肖炳环刘金朝牛留斌罗泽霖陈仕明
肖炳环,刘金朝,牛留斌,邵 奇,罗泽霖,陈仕明
(中国铁道科学研究院集团有限公司 基础设施检测研究所,北京 100081)
波磨指钢轨表面不均匀的波浪形磨耗,是重载铁路中常见的轨道病害。钢轨波磨会加剧轮轨间相互作用,加上重载列车本身的轴重大,异常的轮轨力会破坏车辆和轨道部件,造成疲劳伤损,严重时会影响行车安全。目前尚无有效消除钢轨波磨的技术手段,相比通过钢轨润滑调解轮轨摩擦因数、采用轨道吸振器等措施,打磨被认为是抑制波磨过快发展的有效措施[1]。利用波磨小车人工上道查找钢轨波磨是最直接的办法,然而,上道作业受到天窗时间限制,同时受作业人员操作水平等因素影响,会造成人工查找钢轨波磨的作业效率低下。如何及时高效地发现并评估钢轨波磨成为国内外众多学者研究的重要课题。
1999年,文献[2]采用簧下质量加速度信号的方法,通过研究波兰的铁路信号总结并分析不同波磨区段频谱;2009年,文献[3] 提出基于时频分析技术对钢轨波磨进行诊断,利用ARCAP方法估计波磨的波深和频率;2001年,文献[4]提出了一种基于钢轨表面纹理分析的技术,用于钢轨波磨的检测和分类;2015年,文献[5]采用轴箱加速度测量系统来检测波磨,并提出了一种基于识别出的特征曲线的自动检测算法;2017年,文献[6]提出了一种基于激光摄像技术的波磨检测方法,通过多传感器并行工作对钢轨轮廓进行高频率采样,并将图像的ROI传送至上位机提取轮廓数据,进而完成钢轨波磨信息的提取;2020年,文献[7]提出一种基于参数优化变分模态分解(Variable mode decomposition, VMD)和平滑伪维格纳分布(Smoothed pseudo Wigner-Ville distribution, SPWVD)的轨道波磨辨识方法,信号分解后以包络熵为指标,采用SPWVD方法对分解后的信号进行时频分析,确定波磨发生的位置及波长。
利用图像检测方法诊断钢轨波磨时,受外部环境因素影响较大,容易造成漏判;利用时频分析方法判断数据特性虽然可行,但是由于时频分布的分辨率问题经常导致结果准确率不高。因此本文提出了自适应时频分析和机器学习结合的方法,通过重载铁路综合检测车采集的轴箱加速度信号诊断钢轨波磨。先利用小波包分解(Wavelet packet decomposition, WPD)的方法将信号分解为若干子信号,然后对子信号进行自适应短时傅里叶变换(Adaptive short-time Fourier transform, ASTFT)获得信号高分辨率的时频分布,并提取每个时频分布的熵值作为分类特征,再对特征数据进行降维,最后将所有数据投入支持向量机(Support vector machine,SVM)进行训练和分类。上述基于WPD-ASTFT和SVM的诊断重载钢轨波磨方法通过自适应时频分析可以提高时频分布分辨率,从而提高诊断结果准确率。
1 基础理论
小波包分解能对原始信号进行全频段的细致分解,即在低频段和高频段继续进行分解,可改进小波分解导致的分辨率不能同时兼顾高低频段的问题,从而可以使原始信号的频率分辨率更佳[8]。原始信号s(t)经过n层小波包分解,得到N=2n个子信号,且:
s(t)=s1(t)+s2(t)+…+sN(t)
(1)
式中:t——时间;
si——分解后的第i个子信号,i=1,2,...,N。
对数据采用SVM分类,如图1所示。
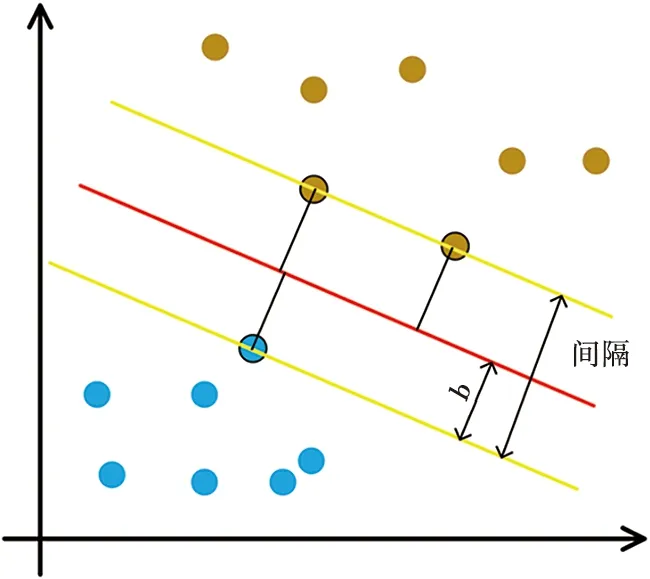
图1 SVM数据分类原理
图1中,两类样本点分布在红色线的两侧,该红色线所在平面称为最大间隔超平面[9],可以表示为:
ωTx+b=0
(2)
式中:ω——平面法向量;
b——支持向量到平面的距离;
x——空间上一点,x=(x1,x2,...,xn)。
样本点到红色线的距离要最大化,空间上一点x到ωTx+b=0的距离为l,表示为:
(3)

对数据进行分类时的分类决策函数h(x)为:
h(x)=sign(ωTx+b)
(4)
sign(x)为sigmoid函数。将预测样本带入分类决策函数中即可得到分类结果[10]。
在已有的基础理论上提出WPD-ASTFT波磨诊断方法,含有多频率成分的信号在进行短时傅里叶变换时,在一个时刻只能选择某一固定窗长,这就使得信号的时频分布分辨率不足,因此,先利用WPD把信号中主频相差较大的频率分解到不同的子信号,这样不同的子信号在同一时刻可以选择不同的窗长进行短时傅里叶变换,然后对不同的子信号进行自适应短时傅里叶变换,通过计算获得使信号时频分布聚集性最好的窗长,称为最优窗长。利用Renyi熵刻画时频分布的聚集性,熵值越小时频聚集性越好。同时窗长与Renyi熵值对应关系作为粒子群优化算法(Particle swarm optimization,PSO)求最优窗长时的适应度函数。
2 自适应短时傅里叶变换和特征提取
2.1 自适应短时傅里叶变换
短时傅里叶变换(Short time Fourier transform, STFT)作为传统时频分析工具,其窗长大小对时频分布的分辨率影响较大,为了避免人工调试窗长并且保证信号做短时傅里叶变换后具有较好分辨率的时频分布,结合Renyi熵和粒子群优化算法提出了自适应短时傅里叶变换。对每个子信号进行自适应短时傅里叶变换,在对应的最优窗长下计算时频分布的Renyi熵[11]。
设某信号包含n个信息y1,y2,y3,…,yn,每一个信息出现的概率是p(y1),p(y2),p(y3),…,p(yn),由它们组成的一个系统S为:
(5)
则这个系统的Renyi熵H(y)为:
(6)
其中,q>0且q≠1。
本文用Renyi熵值作为评判标准,评价时频表示集中度。为使信号做短时傅里叶变换后时频分辨率最佳,需要获取该子信号做短时傅里叶变换时的最佳窗长。因此计算信号在不同窗长下做短时傅里叶变换得到的时频分布STFT(t,f)的Renyi熵Eζ,计算公式如下:
(7)
式中:l——计算系数,为大于0的常数;
α——时间;
β——频率;
T——信号持续时间。
粒子群优化算法相比于遗传算法简单易行,收敛速度快,参数调整方便[12]。若D维空间中有P个粒子,粒子i的位置xi=(xi1,xi2,...,xiD),将xi代入适应函数f(x)求适应值。粒子i的速度vi=(vi1,vi2,...,viD)。粒子i的第d维速度公式更新为:
(8)
式中:pbestid——粒子i个体经历过的最好位置;
gbestd——种群所经历过的最好的位置;
w——惯性权重,非负数,调节对解空间的搜索范围;
c1、c2——均为加速常数,调节学习最大步长,通常c1=c2=2;
r1、r2——均为随机函数,取值范围为[0,1],以增加搜索随机性;
k——迭代次数。
粒子i的第d维位置公式更新为:
(9)

子信号的不同窗长参数设为粒子,做短时傅里叶变换后得到的时频分布的Renyi熵值为适应度函数,计算适应度函数最小时粒子的位置和Renyi熵值。信号经过小波包分解后得到N个子信号。每个子信号主频有所差异,经过粒子群优化过程确定做短时傅里叶变换的最优窗长,对每个子信号si(t)分别和高斯窗函数g做短时傅里叶变换[13]:
(10)
式中:g(ξ-t)——最优窗函数;
f——频率。
经过自适应短时傅里叶变换后,N个子信号在对应的最优窗长下获得Renyi熵值最小的时频分布,同时,在变换过程中Renyi熵值既可以作为分辨率评判标准,又可以在分类过程中作为数据的特征。
2.2 特征指标提取及其降维方法
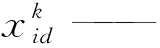
为了提取两类数据Z列熵值差异较大的值作为数据特征,并实现降维,提出均值特征降维法,根据两类数据Z列熵值的平均值差异对数据进行降维处理,具体计算步骤如下:
(1) 计算平均值。
计算正常轨道区段加速度Z列熵值每一列的平均值mi:
(11)
式中:J——正常轨道区段个数;
Oj×i——正常轨道熵值矩阵。
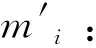
(12)
式中:K——波磨轨道区段个数;
Ck×i——波磨轨道熵值矩阵。
(2) 计算熵值差值。
正常和含有波磨区段Z列平均值对应相减并取其绝对值:
(13)
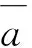
(14)
3 WPD-ASTFT和SVM诊断步骤
基于WPD-ASTFT和SVM的重载铁路钢轨波磨诊断步骤如下:
(1) 将重载铁路轴箱垂向加速度信号按50 m划分为单元;
(2) 各单元信号进行小波包分解,得到若干个子信号;
(3) 每个单元各个子信号进行自适应短时傅里叶变换,并计算时频分布对应的Renyi熵值;
(4) 利用均值特征降维法对熵值数据降维;
(5) 投入SVM分类器训练和预测。
4 试验验证
试验采用国内某重载铁路综合检测列车采集的轴箱垂向加速度信号。将轴箱加速度信号划分为50 m一个单元,一个单元轴箱加速度信号经过小波包分解被分解成若干个频带范围不同的子信号,并且原始信号可由子信号重构:s(t)=s1(t)+…+sN(t),其中N为子信号个数。本文通过三层小波包分解得到8个子信号,并将第6、7、8个子信号相加作为最终的第6子信号,这样既可以节约计算时间,又可以充分分解轴箱加速度信号。
4.1 信号自适应时频特性分析和特征提取
分别选取一段重载铁路正常轨道区段和波磨轨道区段的轴箱加速度信号,如图2所示,正常轨道区段里程为K401+050~K401+100,波磨区段里程为K387+150~K387+200。对2段信号进行三层小波包分解后得到6个子信号,按照WPD-ASTFT步骤计算子信号最优窗长,最后求得时频分布。
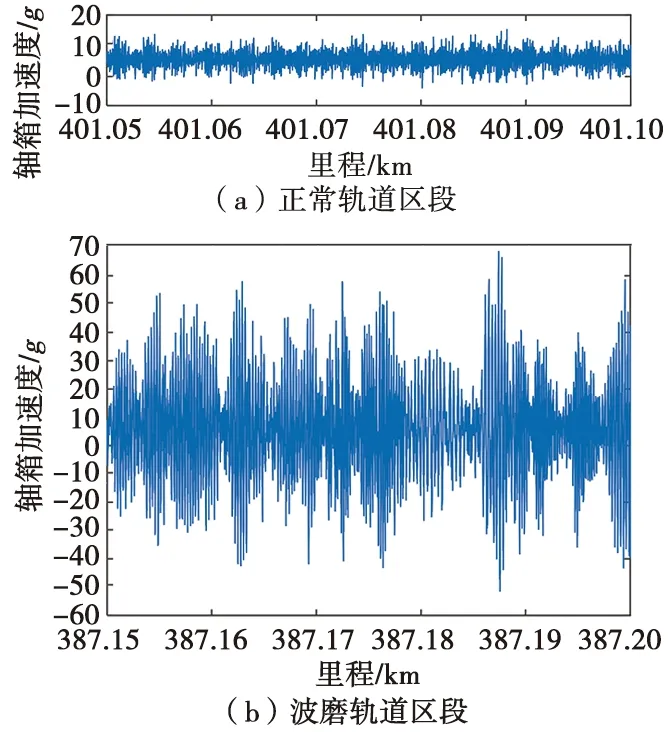
图2 正常和波磨轨道区段轴箱加速度
对正常轨道区段和波磨区段加速度子信号进行自适应短时傅里叶变换,结果如图3所示。由图3可以看出,波磨区段子信号1对应的时频分布中由波磨造成的轴箱加速度的频率集中性明显高于正常轨道区段。计算正常和波磨区段WPD-ASTFT后时频分布对应的Renyi熵值,计算结果如表1所示。
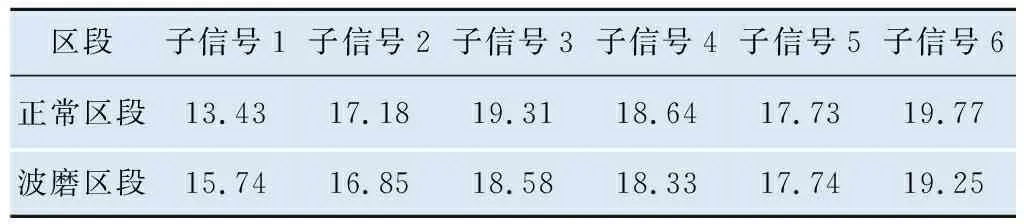
表1 WPD-ASTFT后时频分布对应的Renyi熵值
计算所有区段经过WPD-ASTFT后时频分布对应的Renyi熵值,表2为计算结果,其中1~75为正常区段轴箱加速度信号的Renyi熵值,76~100为波磨区段对应的Renyi熵值。
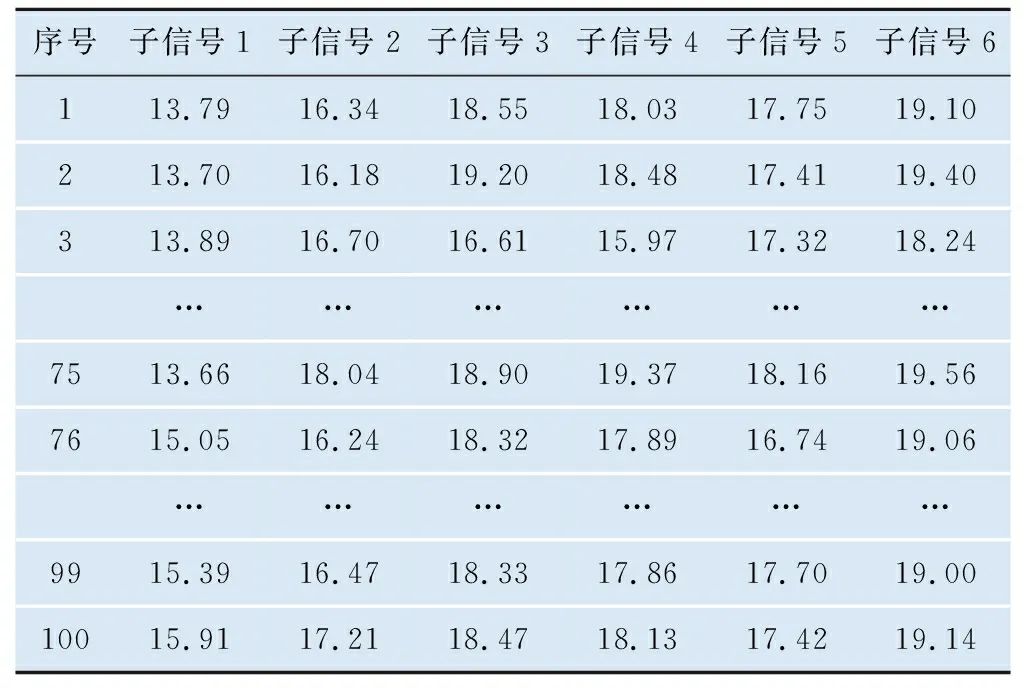
表2 计算所得Renyi熵值
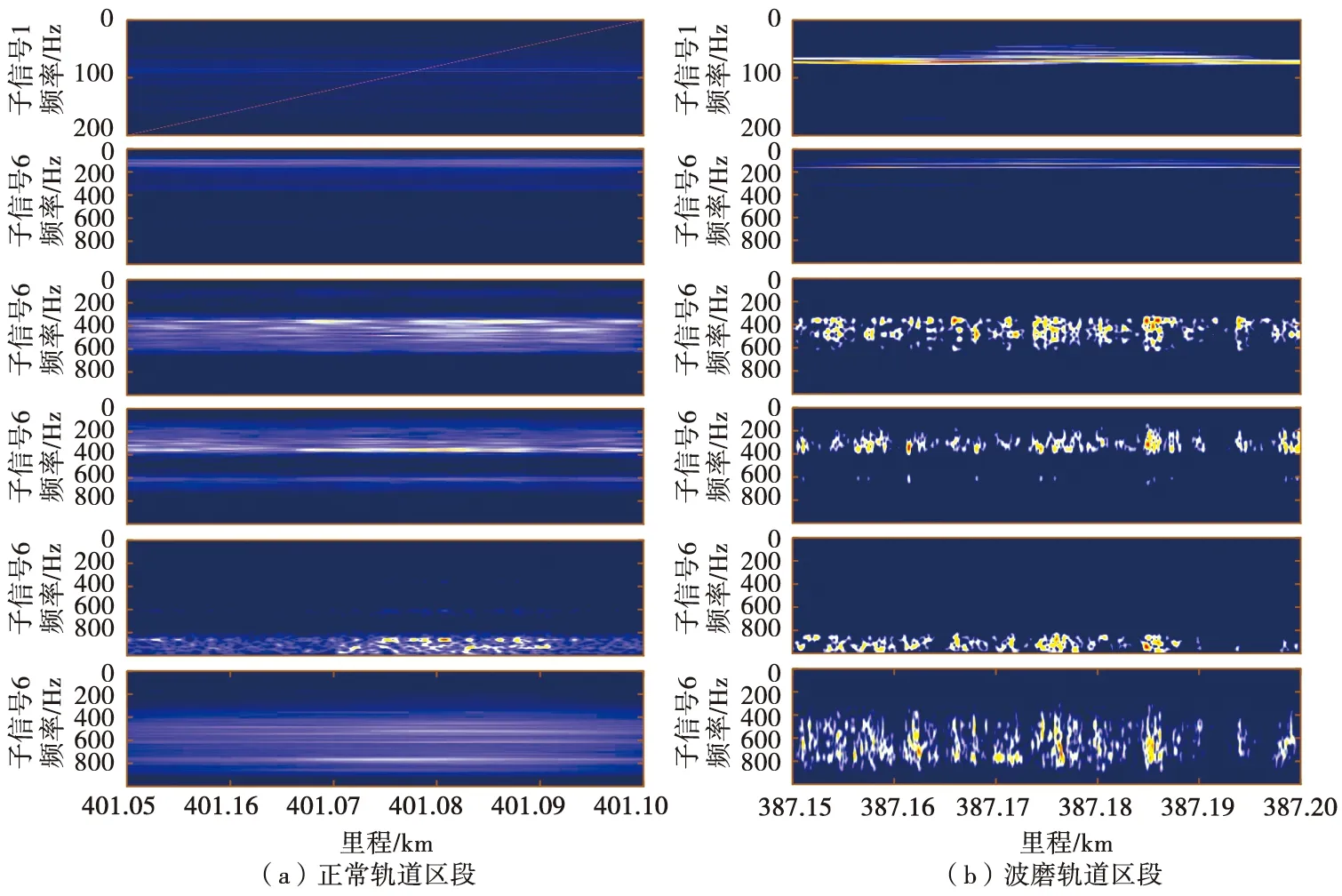
图3 正常和波磨区段子信号对应时频分布
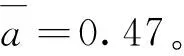
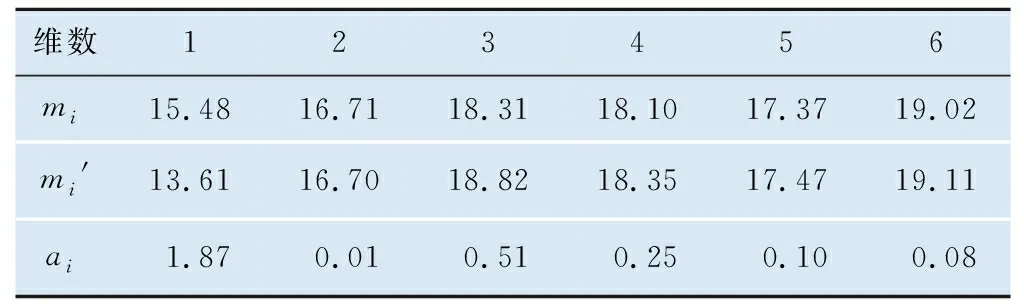
表3 正常区段和波磨区段Renyi熵值的均值和差值
4.2 分类结果
将均值特征降维得到的第一特征熵值和第二特征熵值放入SVM分类器中进行训练。表2中序号1~75为正常区段,标签为‘1’,序号76~100为波磨区段,标签为‘-1’。序号1~100为训练样本,将其投入SVM分类器中进行训练,结果如图4所示,可以看出两类数据被超平面完美分隔。再把测试数据放入分类器进行预测,测试数据同样保留第一特征熵值和第二特征熵值,所有正常区段和波磨区段的训练测试数据及分类结果如图5所示,可以看出15个区段准确预测14个,准确率达93.33%,准确率较高。
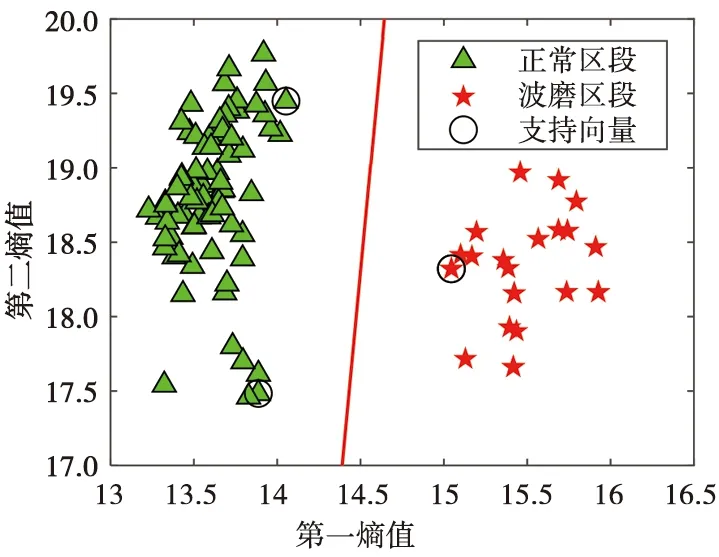
图4 SVM训练结果
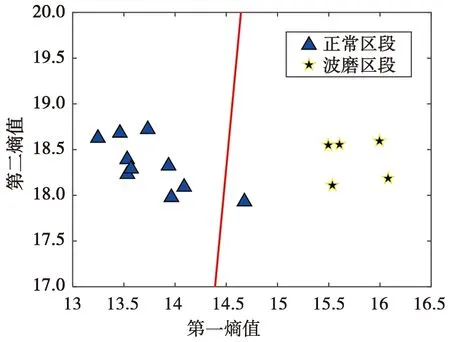
图5 SVM预测结果
5 结束语
本文结合时频分析方法和机器学习,提出了基于WPD-ASTFT和SVM的重载铁路钢轨波磨诊断方法。将该方法应用于诊断重载铁路钢轨波磨,通过预测结果和实际情况对比,验证了方法的可靠性,预测准确率高达93.33%,可以有效指导养护维修工作,抑制波磨的发展。
