旋翼干扰对共轴刚性旋翼振动载荷影响分析

余智豪, 张仕明, 宋彬, 周云

(中国直升机设计研究所 直升机旋翼动力学重点实验室, 江西 景德镇 333001)

突破传统直升机速度限制一直是直升机领域的重要研究方向[1]，以美国Sikorsky公司为代表的国外团队经过几代验证机和型号(XH-59A、X2、S97、SB>1)[2-4]的研制和发展已经证明共轴刚性旋翼直升机是一种极具潜能的高速构型直升机。但随着高速直升机的发展和研制，共轴刚性旋翼动力学问题也逐渐暴露出来，采用“前行桨叶概念”(ABC)[5]，利用升力偏置策略提升旋翼性能和实现高速前飞，但带来了严重的桨根载荷问题，且双旋翼系统以及刚性桨叶设计使得共轴刚性旋翼系统振动载荷更加严重。

XH-59A直升机的飞行试验数据显示在高速飞行状态下驾驶舱垂向振动水平达到0.5g，而横向振动达至0.75g[6]。而X2验证机的飞行试验结果暴露出以400 km/h速度飞行时桨毂俯仰和滚转方向的振动水平出现严重陡增的问题[7]。两者均表明桨毂NbΩ(Nb为单旋翼桨叶片数)谐波载荷为主要振动成分。在马里兰大学风洞中开展的共轴刚性旋翼模型试验[8-9]研究中发现大前进比状态下桨毂俯仰和滚转力矩的2Ω和4Ω(2×2片桨叶)谐波成分相比小前进比时刻增加超过300%，且施加升力偏置也会造成桨毂滚转和俯仰力矩的2Ω谐波成分增加，同时降低了双旋翼桨尖间隙，存在潜在的安全问题。共轴刚性旋翼在工作时存在强烈的双旋翼干扰问题，针对X2旋翼/机身干扰问题开展的CFD/CSD耦合仿真计算研究[10]表明桨叶周期性交叉会引起2NbΩ的强脉冲气动载荷，构成了桨叶2NbΩ结构载荷的主要来源。在德克萨斯州立大学的单片桨叶的共轴双旋翼系统试验中表明[11]悬停时刻桨叶交叉能引起2Ω的挥舞响应以及振动载荷，包括相当于10%旋翼拉力的垂向振动载荷幅值和相当于30%旋翼拉力的拉杆载荷振动载荷幅值。改变上下旋翼的相位关系能影响载荷叠加结果[12]，尤其是桨毂俯仰和滚转力矩，并且具有调节桨尖间距的作用。Gandhi团队利用RCAS软件研究共轴刚性旋翼振动载荷问题[13]时表明优化XH-59A前飞时的俯仰姿态能有效地降低旋翼功率。近些年，国内针对共轴刚性旋翼也开展了较多研究，南京航空航天大学徐国华团队[14]针对悬停状态下的气动干扰进行了研究，表明双旋翼周期性相遇会产生“载荷效应”和“厚度效应”。 用面元法和涡粒子的气动模型[15]研究共轴气动干扰问题时也能捕捉桨涡干扰以及干扰引起的高阶气动载荷，且精度上与CFD方法相当。目前国内针对旋翼干扰下的振动载荷影响研究工作较少，采用CFD/CSD耦合方法能有效提高共轴刚性旋翼振动载荷预估精度，捕捉气动干扰影响下的高阶结构载荷[16]。

本文针对旋翼干扰下的共轴刚性旋翼振动载荷问题，首先建立共轴刚性旋翼气弹分析模型，以XH-59A旋翼为研究对象，详细开展旋翼俯仰角、旋翼间距以及旋翼交叉角对振动载荷的影响分析并总结相应结论，为共轴刚性旋翼振动载荷评估和动力学设计提供理论依据。

1 共轴刚性旋翼气弹分析模型

1.1 共轴刚性旋翼动力学模型

采用广义哈密顿原理，基于中等变量梁理论[17]建立共轴刚性旋翼动力学模型。

(1)

式中：δU为系统应变能变分项；δT为动能变分项；δW为外载荷做功项。动能项包括桨叶旋转产生的动能,而外载荷项包括气动力和气动力矩两部分。

采用5节点15个自由度的梁单元离散桨叶(如图1所示),其中u,v,w,φ表示节点处拉伸、摆振、挥舞和扭转位移。求解每个单元的质量阵、阻尼阵、刚度阵以及外载荷项,最后通过矩阵组集方法得到桨叶动力学方程,如(2)式所示。

(2)

图1 15自由度单元

1.2 共轴刚性旋翼气动模型

采用考虑双旋翼气动干扰的共轴刚性旋翼气动模型,其中入流模型采用自由尾迹模型,桨叶非定常气动力计算采用W-L二阶升力线模型,根据气流无穿透条件(3)式,建立流场速度与环量的关系。

Vi·ni=0

(3)

式中：Vi为桨叶第i个控制点的气流速度;ni为该控制点的法向量,其中Vi包括自由流速度、桨叶运动速度、附着涡诱导速度、近尾迹诱导速度、桨尖涡诱导速度,诱导速度项包含上下旋翼对该控制点的诱导作用。其中附着涡诱导速度和近尾迹诱导速度与桨叶环量分布有关

(4)

VBi为第i个控制点的附着涡诱导速度;AB为桨叶附着涡对控制点的系数矩阵;ANW为桨叶近尾迹对控制点的系数矩阵;Γ为桨叶环量分布;Ns为桨叶分段数。求解桨叶环量分布最终得到桨叶升力分布。通过求解控制方程(5)得到桨尖涡尾迹,其中r(ψ,ζ)为尾迹节点的空间矢量,ψ为方位角,ζ为尾迹寿命角,体现双旋翼干扰。V是桨尖涡线的速度。最后采用预估-修正的迭代方法求解尾迹几何外形。

(5)

1.3 模型验证

本文以XH-59A旋翼作为研究对象,首先计算桨叶模态频率和风洞前飞下的桨叶剖面载荷,并与全尺寸风洞试验[18]数据进行对比,验证模型的准确性,其中旋翼旋转方向为上旋翼逆时针,下旋翼顺时针。旋翼主要参数如表1所示。

表1 XH-59A旋翼参数

图2为桨叶模态频率结果对比图,图中1阶挥舞,摆振和2阶摆振频率吻合度高,2阶挥舞结果存在偏差,但误差不超过8%。

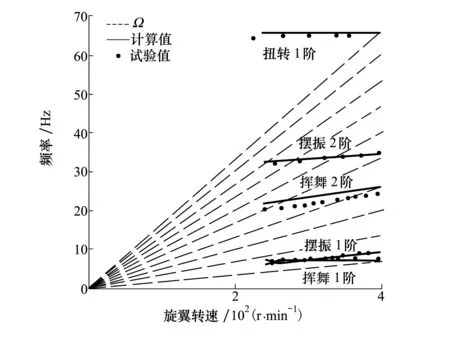
图2 桨叶模态频率

选取2种风洞试验状态,验证对比桨叶剖面载荷,试验状态如表2所示,2个试验状态下半径0.2R挥舞弯矩前4阶谐波幅值计算结果如图3所示。

表2 风洞试验状态

图3a)为run24p10(前进比0.396)状态下的前4阶载荷对比结果,此时桨根挥舞1阶谐波载荷为

图3 谐波幅值

主要成分,2～4阶谐波载荷占比低,同时表明计算结果具有较高的准确性。在run23p13(前进比0.300)状态下,桨根挥舞弯矩以1,2阶谐波载荷为主。在2,3阶谐波载荷对比中,计算值与试验值有一定偏差,因为run23p13状态前飞速度下降,试验中旋翼/机身气动干扰影响增加,而计算分析中未考虑机身模块,故在低阶载荷上出现偏差。

综合模态频率和剖面载荷对比结果,本文采用的共轴刚性旋翼气弹分析模型准确度良好,可信度高。

2 旋翼干扰下的振动载荷特性及影响分析

本节以XH-59A旋翼为研究对象,从俯仰角α,旋翼间距D和旋翼交叉角Ψ这3个对双旋翼气动干扰影响显著的参数展开详细分析。

2.1 俯仰角

在定义俯仰角α时,桨盘低头为负。共轴高速直升机在前飞时俯仰角变化不大,故在小角度范围展开参数影响分析。

图4为前进比μ=0.125状态下2种俯仰角下的旋翼尾迹图。在α=-5°时桨盘前倾(见图4a)),在来流速度和下旋翼诱导作用的影响下,上旋翼桨尖涡脱离后向后下方移动并与下旋翼尾迹汇聚;而下旋翼受上旋翼尾迹诱导作用在桨盘后侧出现向上运动,随后与上旋翼尾迹汇聚一起向后下方运动。而在α=5°时桨盘后倒(见图4b)),此时上下旋翼桨尖涡向后下方移动时会再次穿过桨盘区域,与该区域的尾迹发生干扰和畸变。观察二者俯视图中尾迹畸变和运动,在α=5°时,尾迹呈扩散态势。俯仰角变化直接改变了桨盘区域附近的流场环境,并改变旋翼尾迹的运动,必然会引起桨叶上的气动、结构载荷的变化,最终引起桨毂振动载荷变化。

图4 旋翼尾迹

选取前进比μ=0.125和μ=0.35配平状态下展开计算分析,其中α变化区间为[-3°,3°],配平目标为桨毂垂向力Fz,桨毂滚转力矩Mx和桨毂俯仰力矩My。图5～6为μ=0.125状态下的旋翼桨盘升力云图。对比结果可观察到:在配平条件下桨盘升力区集中在桨叶外端,而α=3°时升力集中区域减小,表明这些区域受到了更强的尾迹干扰,导致桨叶升力下降,同时升力分布的变化也必然会引起桨毂滚转和俯仰力矩发生变化。

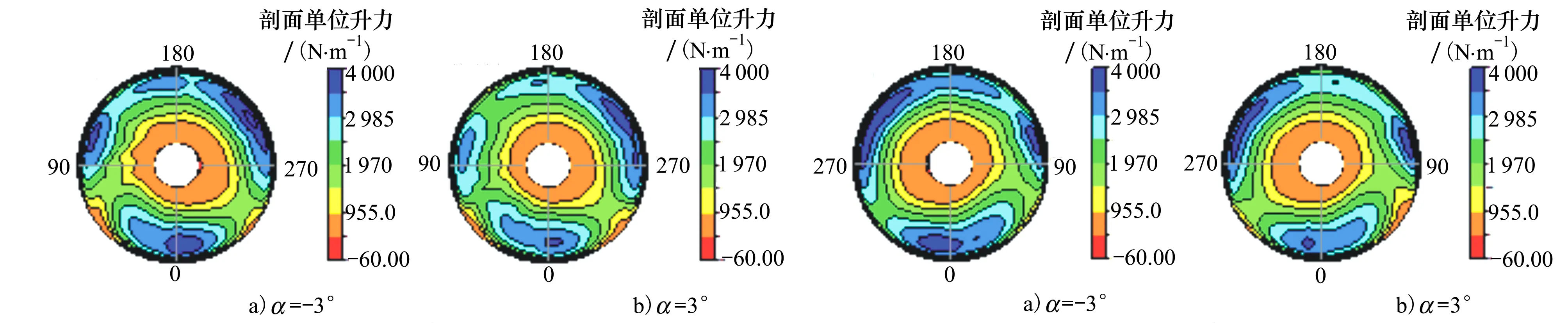
图5 下旋翼桨盘升力云图图6 上旋翼桨盘升力云图

桨毂振动载荷主要以桨叶片数的整数倍谐波载荷为主,其中桨毂载荷主要成分为Fz,Mx和My。图7为μ=0.125状态下桨毂3Ω和6Ω谐波幅值结果。由图7a)可以看出，桨毂垂向力Fz的3Ω谐波幅值随α增大而降低,6Ω谐波幅值变化不大。垂向力Fz的谐波载荷主要来源于旋翼升力变化,图6升力云图也反映出在α=3°时,升力集中区域(0°,90°,270°)减弱,进而使得升力谐波振荡减弱,最终使得桨毂Fz的3Ω谐波幅值降低。由图7b)可以看出，桨毂滚转力矩Mx的3Ω谐波幅值随俯仰角增加而急剧增加,6Ω谐波幅值降低。俯仰角增加后,旋翼尾迹干扰效应加剧且存在尾迹二次穿过桨盘区域现象,使得桨盘横向升力产生剧烈振荡,尤其是桨涡干扰、尾迹畸变最严重的90°和270°度附近。图7c)中桨毂俯仰力矩My的3Ω和6Ω谐波幅值均降低,而桨盘180°附近来流将尾迹吹向后方,受气动干扰影响较低,主要影响0°区域附近,进而导致了俯仰角在增加过程中虽然尾迹干扰变严重了,但桨毂俯仰力矩载荷降低。图7结果还表明旋翼尾迹干扰主要影响气动力的低阶成分,对桨毂高阶谐波载荷影响较低。

图7 双旋翼桨毂谐波载荷

图8为μ=0.35时刻桨毂3Ω和6Ω谐波幅值计算结果。桨毂垂向力Fz(见图8a))和桨毂俯仰力矩My(见图8c))的谐波载荷与μ=0.125时趋势一致。值得注意的是桨毂滚转力矩Mx的3Ω谐波幅值先增大后减少,因为在μ=0.35时,来流速度增大后,桨尖涡脱离后离开桨盘而并没有二次穿过桨盘,一定程序上减弱了旋翼尾迹干扰对桨叶气动力的影响,进而降低了振动载荷。

从2种前进比状态的结果可知,俯仰角增加使得桨毂Fz和My谐波幅值降低,而Mx谐波幅值增加,侧面表明俯仰角能一定程度上调节桨毂振动载荷水平。

图8 双旋翼桨毂谐波幅值

2.2 旋翼间距

旋翼间距D是反映上下旋翼桨毂中心距离的参数。图9为μ=0.125时2种旋翼间距下的旋翼尾迹图。在D=0.20R时,下旋翼尾迹并未穿过上旋翼桨盘,桨盘后方尾迹汇聚后的畸变效应也比D=0.14R时弱。

图9 旋翼尾迹

为减少高速前飞的桨毂阻力,旋翼间距设置在0.14R[18]。本节对前进比μ=0.125状态下的0.14R,0.16R和0.18R3种旋翼间距展开载荷特性分析,在配平状态下(配平目标不变)得到以下结果。

图10为2种间距下的上旋翼桨盘升力云图,升力分布差别不大。在0.18R间距下升力集中现象减弱。图11为桨毂Fz,Mx,My谐波幅值计算结果,间距增大后,3Ω和6Ω幅值均降低,且桨毂Fz和My的6Ω幅值下降幅度更大,但桨毂Mx的3Ω幅值在0.18R状态有所增加,表明旋翼间距增大后,旋翼间的干扰效应减弱的同时,自身的桨涡干扰效果增加,引起了高阶气动力的增加,尤其是在尾迹脱出汇聚的90°和180°区域,引起桨盘横向的不平衡性,产生了滚转力矩Mx。

图10 上旋翼桨盘升力云图

图11 双旋翼桨毂谐波幅值

2.3 旋翼交叉角

旋翼交叉角Ψ是反映上下旋翼桨叶周期性交叉的参数,通过改变相位关系来改变上下旋翼载荷叠加和最终载荷结果。以3片桨叶为例,上下旋翼单片在一个周期内交叉6次(如图12所示),在前飞状态下,不同交叉角必然引起不同的气动干扰效果,导致桨叶高阶气动力的变化,进而改变结构载荷,并且直接双旋翼桨毂载荷相位叠加,最终会导致共轴刚性旋翼桨毂振动载荷的变化。

在μ=0.125状态下分析0°和30°交叉角下的振动载荷,结果如图13和图14所示。在配平状态下的桨盘升力结果中观察到:在Ψ=30°时,升力分布的不均匀性增加,其中0°，90°和180°区域附近的升力集中效应增强,桨尖位置的升力振荡变化更剧烈,最终会增加桨毂载荷高频部分。

图12 双旋翼交叉角 图13 上旋翼桨盘升力云图

图14a)为桨毂Fz的谐波幅值计算结果,在Ψ=30°时Fz的3Ω幅值增加,这是桨盘部分区域升力集中导致(见图13b)),但6Ω幅值降低,与两幅旋翼载荷叠加有关。在Ψ=30°时Mx谐波幅值增大,My减小,但Mx谐波幅值增加量更大。综合考虑振动结果,0°交叉角的振动水平略优于30°交叉角。

图14 双旋翼桨毂谐波幅值

3 结 论

本文以XH-59A旋翼为研究对象,建立共轴刚性旋翼气弹分析模型并进行对比验证,针对旋翼干扰下的共轴刚性旋翼振动载荷问题详细地开展了参数影响分析,并得到以下结论:

1) 俯仰角α主要影响上下旋翼桨叶桨尖涡脱离后的畸变与尾迹干扰效应,主要影响桨毂NbΩ(Nb为桨叶片数)谐波载荷,α增大(即桨盘抬头)则桨毂垂向力Fz和俯仰力矩My谐波载荷降低,其中垂向力Fz的3阶谐波幅值在计算区间内最大可降低42%,俯仰力矩My的3阶谐波幅值最大降低30%;而小前进比状态下滚转力矩Mx的3Ω谐波幅值增大,但大前进比状态Mx的3Ω谐波幅值先增大后减小。研究表明控制共轴刚性旋翼高速前飞的俯仰姿态是一种潜在的减振手段。

2) 旋翼间距D通过改变上下旋翼尾迹干扰的程度来影响桨毂振动载荷,旋翼间距越低,振动问题更严重,在本文计算区间内桨毂垂向力Fz的3阶幅值最大增加23%,6阶幅值最大增加30%。

3) 前飞时交叉角Ψ对桨毂滚转力矩Mx和俯仰力矩My影响明显,前飞时Ψ=0°桨毂振动载荷水平低于Ψ=30°状态下的桨毂振动载荷水平。