基于多目标优化的危废焚烧配伍模型研究
2022-01-10郝亮钧楚金旺
郝亮钧,楚金旺,姚 心,庞 慧,3,陈 鑫
(1.中国恩菲工程技术有限公司,北京 100038;2.中国矿业大学(北京)力学与建筑工程学院,北京100083;3.北京科技大学 机械工程学院,北京 100083)
0 引言
危险废物主要指具有腐蚀性、毒性、易燃性、反应性或者感染性等一种或者几种危险特性的废物[1]。对于危险废物处置不当,不仅会对人体健康造成直接危害,同时也会在自然环境中发生迁移转化,进而对土壤、水体和大气等生态环境造成污染。危废经过焚烧处置,除重金属以外的其它有害成分可被充分分解和消灭,减量化效果显著,同时焚烧产生的热量可回收利用,用于供热和发电,具有可观的经济效益[2-3]。
其中,危废配伍是危废进入焚烧系统之前的必要操作过程,即结合各拟焚烧物料粒径、热值、水分、挥发分、硫氯含量、灰渣特性等物理及化学性质,实现不同物料燃烧特性的有效融合,使焚烧系统能够持续、稳定、经济运行。
目前,关于危废焚烧处置配伍方法的研究,主要集中于单个目标最优,很少考虑多目标同时最优的情形,尤其是焚烧处置系统综合处置量和企业经济效益同时达到最优的状态[4-7]。2017年[8],重庆大学张宏良以重庆市某水泥厂为例建立了水泥窑替代燃料原料焚烧配伍模型,用于验证现场配伍数据的合理性,但并未给出最优配伍方案的求解方法;2018年[9],四川大学梁学栋等提出了一种危废配伍方法,通过对焚烧指标矩阵进行求解计算,得到各种危废的配伍权重,但并未表述配伍原则的控制途径;2019年[10],光大环保技术研究院(南京)有限公司在考虑各配伍原则的基础上,提出了一种以日处理量最大为目标的配伍方法,而并未考虑经济效益最大。此外,缺乏关于多目标最优的配伍算法研究,使多目标配伍方案的现场实施应用存在困难。
为此,本文基于多目标优化方法,同时考虑综合处置量和经济效益最优,构建了多目标优化的危废配伍模型,并通过多目标函数的加权求解方法,获得最优配伍方案,不仅能够保证危废焚烧处置系统的最大运行能力,同时能够兼顾危废处置企业的最大经济效益。
1 配伍模型的建立
1.1 配伍原则
在保证物料相容性的基本条件下,还需满足以下两个主要条件:
(1)保证合适的热值。
通过配料将热值控制在合适的范围之内。避免热值过高,使窑内温度超过耐火材料能够耐受的最高温度,而造成的安全问题;同时,避免热值过低,补充天然气等其他辅助燃料,而增加的运行成本。
(2)控制有害物质占比。
控制酸性物质、卤化物、重金属、碱金属等有害物质的占比,进而控制产生烟气的有害气体含量,从而一方面避免对设备产生腐蚀损坏,另一方面保证满足系统的净化能力,烟气能够排放达标。
1.2 配伍模型
假定现有n种废物进入焚烧系统协同处置,其中a1,j、a2,j、a3,j、a4,j、a5,j、a6,j、a7,j、a8,j、a9,j、a10,j、a11,j、a12,j、a13,j、a14,j、a15,j、a16,j分别表示第j(1≤j≤n,且j为整数)种废物中的有机碳含量(质量%)、无机碳含量(质量%)、H含量(质量%)、O含量(质量%)、N含量(质量%)、P含量(质量%)、S含量(质量%)、Cl含量(质量%)、F含量(质量%)、重金属含量(ppm)、碱金属含量(ppm)、H2O含量(质量%)、热值(kcal/kg)、处置量(kg/盘)、处置成本(元/盘)、经济效益(元/盘);bi和ci分别表示处置系统对第i(1≤i≤16,且i为整数)个指标处置能力的下限值和上限值,如果下限值不存在,则取bi=-∞,如果上限值不存在,则取ci=∞;dj表示第j中废物的库存量(盘)。构建相关指标参数矩阵:

设xj为第j种废物的处置量,可知,xj为大于零的正数。令:

则入窑处置废物中,有机碳的总含量为a1,1x1+a1,2x2+…+a1,nxn,表示成矩阵形式为a1,:x,根据废物配伍原则,需满足约束不等式b1≤a1,:x≤c1。同样地,可得第i个项目需满足的约束不等式为bi≤ai,:x≤ci,其中,ai,:=[ai,1,ai,2,…,ai,n],表示矩阵A中第i行元素,即各废物关于第i个指标的数值。焚烧配伍满足的约束条件为:

另一方面,各废物的处置量不应该超过各废物目前的库存量,即xj≤di。则废物处置量满足的约束条件为:

实施上述配伍规则,处置系统单次综合处置量、单次运行的经济效益分别为:
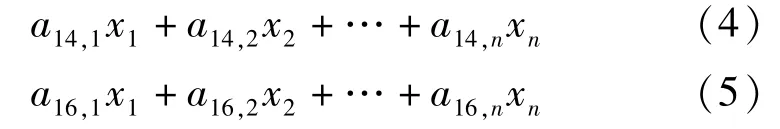
表示成矩阵形式为:

由此建立处置系统单次运行综合处置量最大,且济效益最大的配伍模型为:

2 配伍模型的求解
引入剩余变量和松弛变量,将配伍模型(8)转化为标准型:

其中,xb为n维剩余变量:

xc和xd为n维松弛变量。

利用专家打分法或加权因子分解法等,确定各个目标函数的权重系数,保证着重考虑的模型目标具有较大权重,设wk为第k个模型目标的权重。依据不同模型目标的权重系数,将多目标模型转换为新的单目标加权模型:

新的目标模型为单目标规划模型,求解可得整个模型的最优解。
3 案例分析
以某危废处理厂为例,假设有4种物料,配伍物料和处置系统的相关指标参数,如表1所示。

表1 配伍物料和处置系统的相关指标参数
设xj为第j(j=1,2,3,4)种废物的处置量,建立焚烧系统综合处置量和经济效益最大的配伍模型,求解可得不同权重分配下的配伍方案,如表2所示。

表2 不同目标权重下的配伍方案
4 结论
基于多目标优化方法和加权求解算法,得到了兼顾处置系统最大运行能力和处置企业最大经济效益的最优配伍方案,不仅能够满足焚烧处置系统的持续稳定运行,而且可以为企业在不同生产负荷和不同市场环境下提供最佳的配伍方案。
