基于奥美拉唑在水和乙醇二元溶剂体系中热力学模型的分析
2022-01-10戴明明董文侠张桂兵王金峰陈夏夏
吴 刚,吴 伟,戴明明,董文侠,张桂兵,陈 强,李 新,王金峰,陈夏夏
(南京正大天晴制药有限公司,江苏南京210038)
奥美拉唑是一种白色粉末或类白色粉末状固体,分子式为C17H19N3O3S(图1),其化学物质登记号(CAS)为73590-58-6,是由一个亚砜链连接到苯并咪唑的取代吡啶环组成。作为胃质子泵H+/K+-ATP酶的可逆抑制剂,奥美拉唑及其制剂常被广泛应用于胃溃疡、十二指肠溃疡、反流性食管炎和卓-艾综合征的治疗[1-3]。奥美拉唑是目前国际上使用最为广泛的处方药之一,同时在一些国家也被作为非处方药进行销售。奥美拉唑及其衍生物具有较高的医药使用和工业生产价值。

图1 奥美拉唑的化学结构式Fig.1 Chemical structure of omeprazole
众所周知,纯化处理是药物生产的重要组成部分。药物溶解度及其性质在固-液相平衡、液-液相平衡中具有重要作用。本文旨在对奥美拉唑的固-液相平衡数据进行收集、拟合和分析,以期为奥美拉唑的工业生产与使用提供基础数据。此外,基于基础数据还可以进一步探讨关于奥美拉唑的结晶和萃取等工艺问题。
采用质量法,测定了常压下奥美拉唑于278.15~333.15 K,在混合溶剂(水和乙醇)中的溶解度,并将溶解度数据采用修正的Apelblat模型、近理想二元溶剂/Redich-Kister(CNIBS/R-K)模型和Jouyban-Acree模型进行拟合。同时利用范德霍夫分析和吉布斯方程,计算热力学参数(包括焓、熵和吉布斯自由能)。根据实验数据,从混合溶剂中找出奥美拉唑结晶和萃取过程中的相平衡规律。此外,热力学性质分析也有助于确定最佳温度区间,并得出不同温度下溶解度的变化趋势[4],以补充奥美拉唑的基础理论研究,以期为其纯化萃取工艺提供一定指导,也对奥美拉唑的使用、药物制剂开发和清洁等方面提供参照。
1 实验
1.1 材料与仪器
奥美拉唑(纯度≥98.0%),上海德默医药科技有限公司;蒸馏水,南京正大天晴公司超纯水系统生产,其电导率标准≤0.80 μS/cm(25 ℃);实验所用材料的详细信息见表1。BS124S型分析天平,北京赛多利斯科学仪器有限公司,量程为0~120 g,精度值为±0.1 mg;WDC-0540型循环恒温水浴系统,南京舜玛仪器设备有限公司,量程为268.15~373.15 K,精度值为±0.1 K。

表1 化学试剂属性
1.2 实验方法
实验通过质量法进行溶解度的测定,采用文献[5-6]中所述的方法,即将过量的奥美拉唑与不少于8 mL的有机溶剂加入带塞子的10 mL玻璃试管中(避免实验过程中溶剂蒸发)。将所有玻璃试管置于循环恒温水浴系统中,开启磁力搅拌器连续搅拌24 h以上,以确保玻璃试管中的液体达到平衡。关闭搅拌并保持温度至少6 h,以确保未溶解固体在玻璃试管的底部沉淀。用移液枪吸取1 mL透明澄清的饱和溶液,迅速转移至5 mL已称质量的烧杯中。立即称量含有溶液的烧杯总质量,然后将烧杯置于室温下的干燥器中。定期(如每星期一次)对烧杯称质量,直至质量没有变化。为了检查溶解度测定的重复性,每个实验至少重复3次。用同样的方法,在不同的温度下测量了3个样品的溶解度,并用平均值计算了溶解度的摩尔分数。以摩尔分数表示的溶解度(x)的计算见式(1)~(2)。
(1)
(2)
式中:xA为二元溶剂中乙醇的摩尔分数;m1、m2和m3分别代表奥美拉唑、乙醇和水的质量;M1、M2和M3分别代表奥美拉唑、乙醇和水的摩尔质量。
2 结果与讨论
2.1 数据与模型
在278.15~333.15 K温度范围内,将奥美拉唑在二元溶剂混合物(水和乙醇)中的溶解度(x)记录于表2。
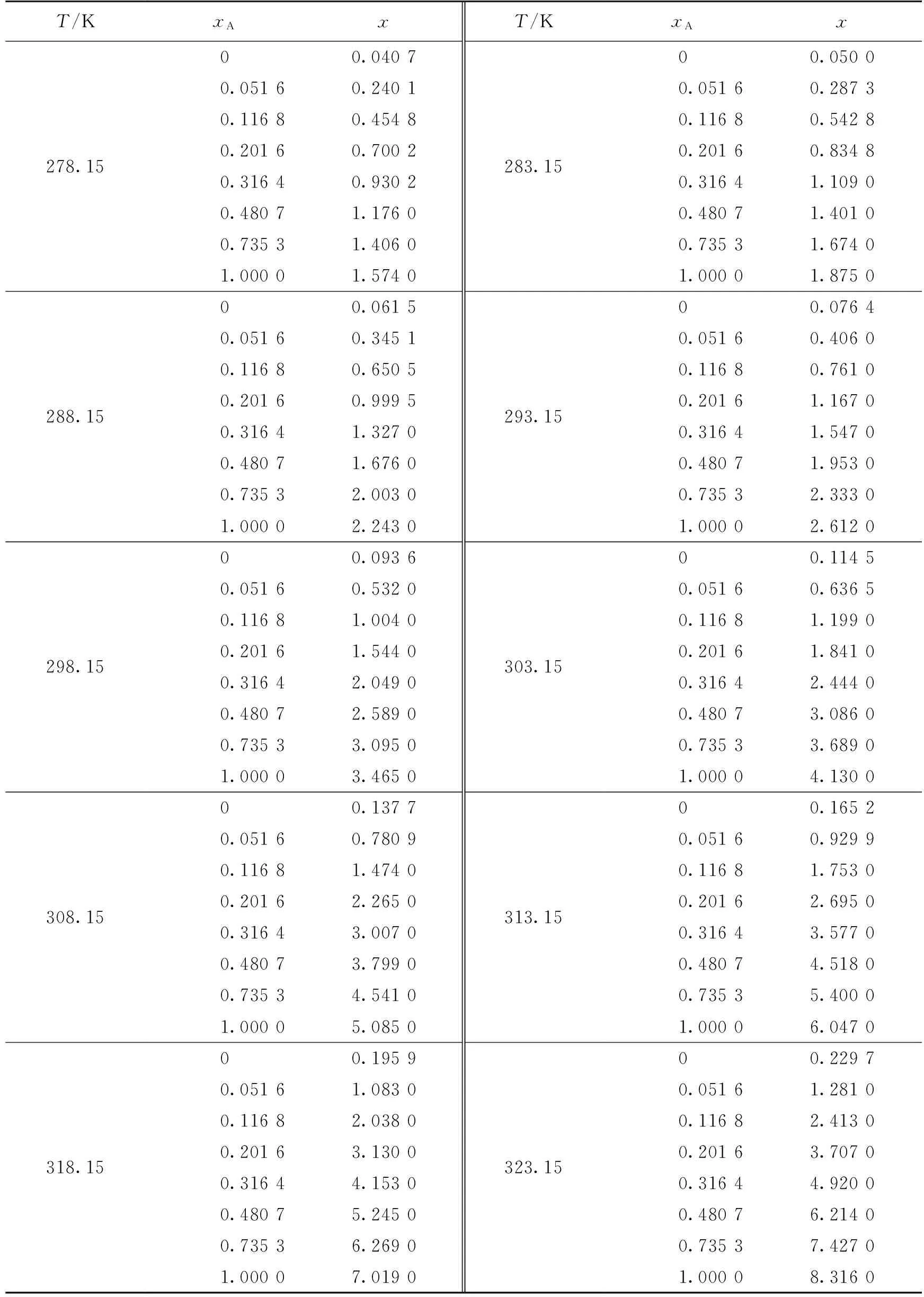
表2 奥美拉唑在二元溶剂(水和乙醇)中的溶解度(x)
由表2和图2可知:奥美拉唑在二元溶剂混合物(水和乙醇)中的溶解度随温度升高而增加,恒温时,奥美拉唑的溶解度随二元溶剂中乙醇含量的增加而增加。
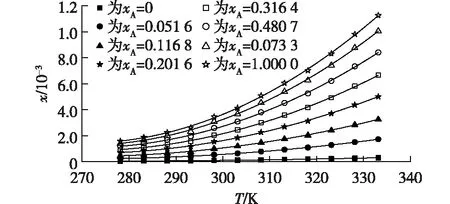
图2 二元溶剂体系中奥美拉唑的溶解度(x)与温度(T)的关系Fig.2 Solubility(x) of omeprazole versus temperature(T) in the binary solvent mixtures
2.1.1 修正的Apelblat模型
奥美拉唑溶解度随温度变化的变化关系可利用修正的Apelblat模型进行拟合[7-9],得到式(3)。
(3)
式中:T代表绝对温度(K),因子A和B代表溶液活度系数的变化,表示溶质溶解度的非理想溶液效应,因子C表示温度对熔融焓的影响,即热容(ΔCp)[10-11]的修正;x代表奥美拉唑二元溶剂中的溶解度。修正后的Apelblat模型回归曲线参数见表3。由表3可知:奥美拉唑二元溶剂体系在修正的Apelblat模型的标准偏差(RMSD)为3.39×10-4。
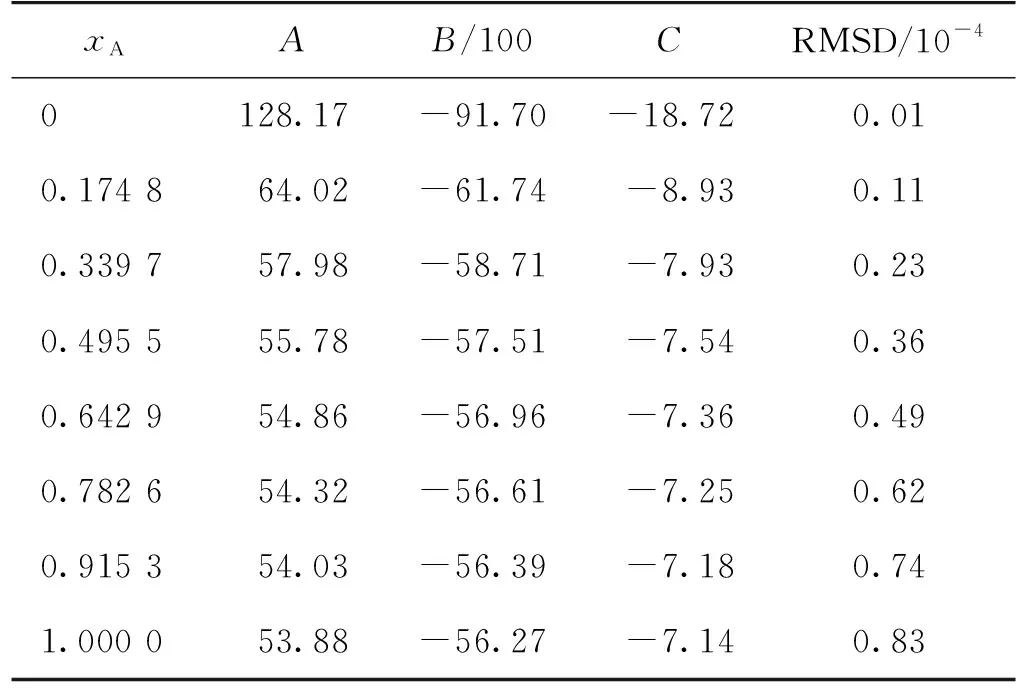
表3 奥美拉唑二元溶剂体系在修正的Apelblat模型的参数
2.1.2 CNIBS/R-K 模型
近理想二元溶剂/Redich-Kister(CNIBS/R-K)模型也是计算二元溶剂中溶质溶解度的理论模型之一[12-16]。等温条件下,溶解度随混合溶剂中乙醇摩尔分数的变化趋势常用CNIBS/R-K 模型进行拟合,CNIBS/R-K 模型可用式(4)表示。
(4)
式中,x代表奥美拉唑的溶解度;xA和xB代表未添加溶质时二元溶剂的初始摩尔分数;XA和XB分别代表奥美拉唑在纯乙醇和纯水中的溶解度;Si是模型常数;N可以等于0,1,2,3,i,无实意。当N=2时,可用(1-bxA)代替xB,其中b代表溶液中的一个组分,则式(4)可重排为式(5)。
lnx-(1-xA)lnXB-xAlnXA=
(1-xA)xA[S0+S1(2xA-1)+S2(2xA-1)2]
(5)
这是CNIBS/R-K 模型的一种变形,参数Si可以通过拟合{lnx-(1-xA)lnXB-xAlnXA}与{(1-xA)xA[S0+S1(2xA-1)+S2(2xA-1)2]}得到。
拟合得到的参数值见表4。由表4可知:CNIBS/R-K模型只能用来描述溶解度数据和预测不同浓度混合溶剂在固定温度下的溶解度数据。为了描述溶剂组成和温度对奥美拉唑溶解度的影响,可采用Jouyban-Acree 模型。奥美拉唑二元溶剂体系在CNIBS/R-K模型的RMSD为29.33。
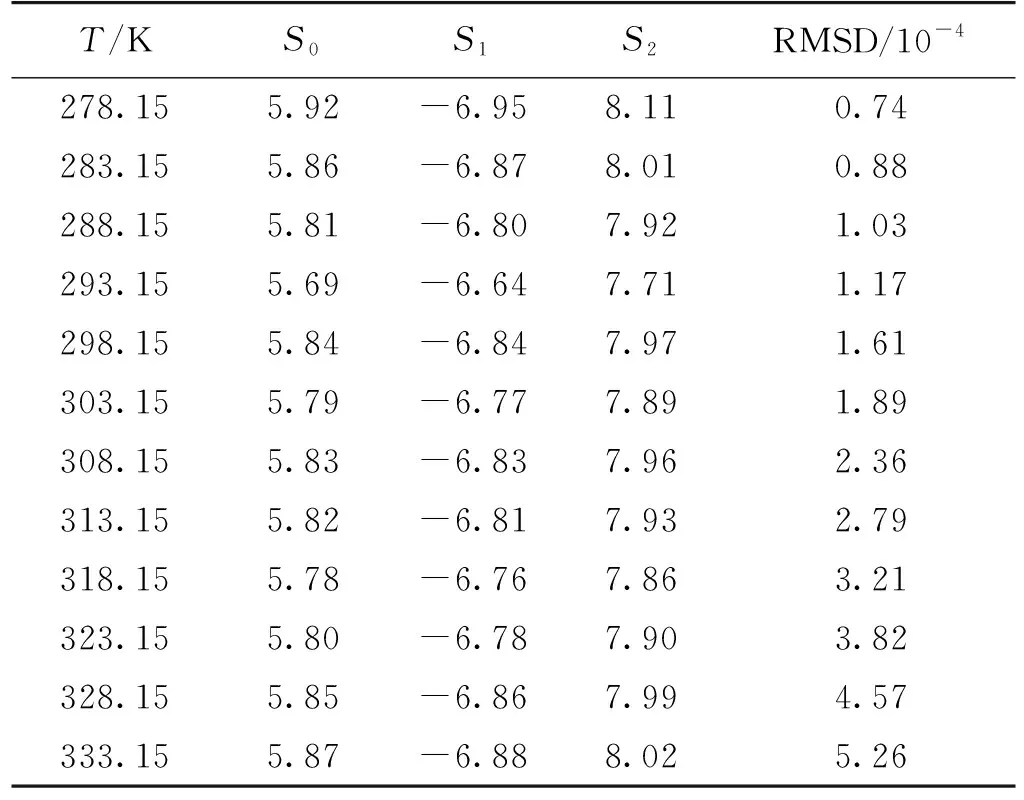
表4 奥美拉唑二元溶剂体系在CNIBS/R-K模型的参数
2.1.3 Jouyban-Acree 模型
Jouyban-Acree 模型是一种描述溶质溶解度随温度和二元溶剂初始组分的变化而变化的常见模型[17]。
(6)
式(6)中,Ji是模型常数;T是绝对温度(K);其他符号的含义与式(4)含义相同。当N=2时,可用(1-bxA)代替xB,由式(6)可得到式(7)。
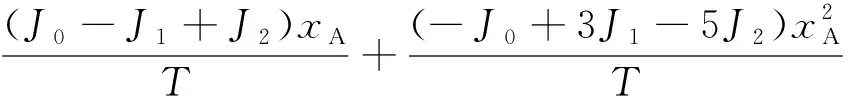
(7)
由式(7)可以进一步简化为式(8)。
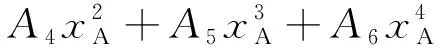
(8)
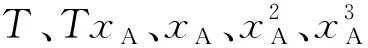

表5 奥美拉唑二元溶剂体系在Jouyban-Acree模型的参数
由表5可知:修正的Jouyban-Acree模型的RMSD值为16.30×10-4。结果表明:修正的Apelblat模型拟合效果最好。因CNIBS/R-K模型和Jouyban-Acree模型更多阐述二元溶剂比例对溶解度的影响关系,可以通过上述2种模型实现对修正的Apelblat模型的补充完善。
2.1.4 RMSD
RMSD是用以描述预测值与真实值的偏差情况,也常用于衡量实验数据与计算数据的偏差[18]。本实验中用其评估比较各模型与实验数据的拟合适用情况,相对偏差数据见表6。由表6可知,修正的Apelblat模型在温度较低情况下,其相对偏差值相对较大,随着温度的升高,相对偏差值逐渐变小;而就CNIBS/R-K 模型、Jouyban-Acree 模型而言,在乙醇比例低的情况下,其相对偏差值相对较大,随着乙醇比例的逐渐变大,相对偏差值逐渐变小。此现象可考虑为溶解度数值相对较小时,其相对偏差值可能相对较大。RMSD的计算方法见式(9)。
(9)

表6 奥美拉唑不同摩尔分数(xA)下溶解度(x)在各模型下相对偏差
式中:N表示实验点的个数;x和xcal分别表示实验数据和计算数据。
3.1.5 热力学参数
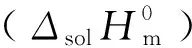
(10)
式中:R为通用气体常数(8.314 J/(mol·K),T表示绝对温度(K)。平均温度时标准摩尔溶解焓亦可用上式表达[19-20]。由此可以得到式(11)。
(11)
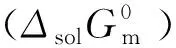
(12)

图3 二元溶剂体系中奥美拉唑的摩尔分度溶解度(ln x)对应(1/T-1/Tmean)的范德霍夫分析图Fig.3 Mole fraction solubility(ln x) of omeprazole versus temperature(1/T-1/Tmean) in the binary solvent mixtures
(13)
(14)
(15)
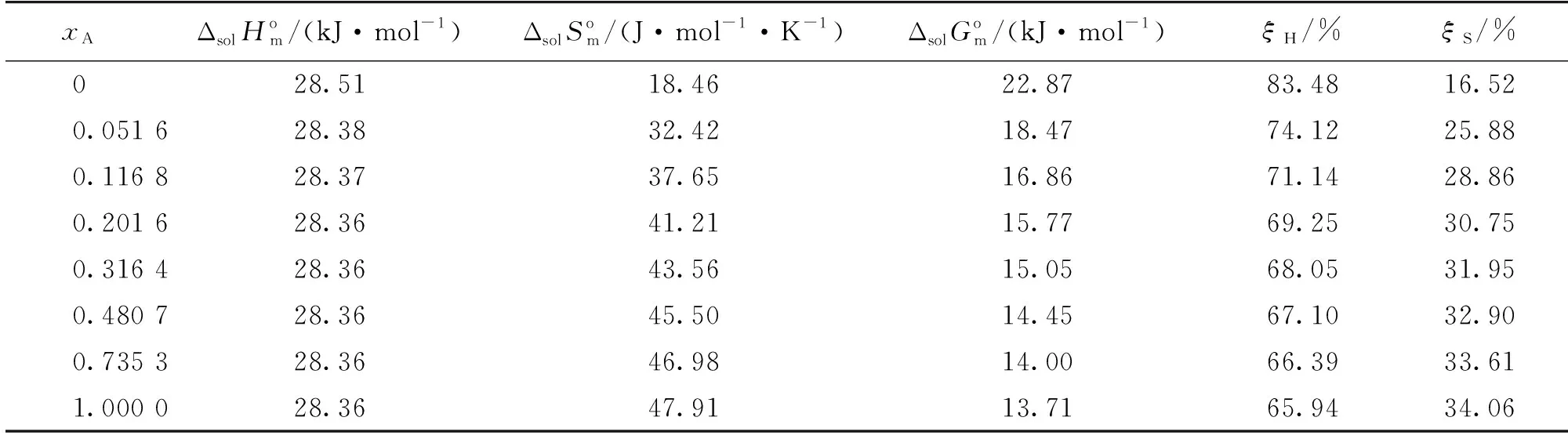
表7 平均温度下奥美拉唑在二元溶剂体系溶解过程的热力学函数
3 结论
可以根据以上图表数据及分析得出以下结论:
1)奥美拉唑在二元溶剂(水和乙醇)中的溶解度随着温度的升高而增加,随着乙醇比例的增加而增加;
2)所采用的修正的Apelblat方程、CNIBS/R-K模型和Jouyban-Acree模型均可成功拟合溶解度数据,其中修正的Apelblat方程因RMSD值最小而拟合情况更好,并可以通过其他2个模型实现对修正的Apelblat模型的补充完善;
3)根据范德霍夫分析的热力学参数和吉布斯方程可知,奥美拉唑在二元溶剂(水和乙醇)体系中的溶解过程是吸热的,非自发的。
上述结论能为优化奥美拉唑的纯化萃取工艺提供一定指导,同时在实际工业生产中,对奥美拉唑的使用、药物制剂开发等方面的研究提供一定的参考意义。
