基于IGM-WOA-SVM的埋地管道腐蚀深度预测技术研究

李金松，赵元东，宋明垚，田东海，梁昌晶

1.中国石油华北油田公司发展计划部，河北任丘 062552

2.中国石油华北油田公司二连分公司，内蒙古锡林浩特 026000

3.中国石油华北油田公司巴彦勘探开发分公司，内蒙古巴彦淖尔 015000

我国大部分陆上和海上油气管道已进入事故多发期，根据2006—2018年的失效数据统计，因腐蚀造成的管道失效占失效总次数的32%，因此对管道腐蚀深度和剩余寿命进行准确预测是加强管道完整性管理的一项重要工作[1]。目前，国内学者已针对腐蚀深度的预测进行了大量研究。骆正山[2]等采用Frechet极值分布预测了管道最大腐蚀深度，但未针对预测误差进行评价；张新生等[3]采用GM（1，1）模型预测了管道腐蚀深度，并利用马尔科夫链对剩余寿命进行了预测，但腐蚀深度预测值的最大相对误差为10.41%；胡群芳等[4]通过对模型参数的分布进行贝叶斯估计，根据MCMC方法对不同样本独立性区间内的腐蚀深度进行预测，但未对预测结果进行评价；王文辉等[5]采用PSO-GRNN模型对管道剩余寿命进行了预测，其最大相对误差为13.77%，平均相对误差为6.63%。以上研究大都采用单一方法对腐蚀深度进行预测，且模型的适用性和可靠性均有待提高。考虑到影响埋地管道腐蚀的因素具有随机性和差异性，本文采用改进的GM（1，1） 模型（IGM） 对腐蚀深度进行预测，采用WOA（鲸鱼优化算法）-SVM（支持向量机）模型对IGM的预测误差进行修正，形成误差补偿器，克服单一模型预测的不足，构建适合埋地管道腐蚀深度的预测模型，为管道完整性管理提供理论依据和实际参考。

1 GM（1，1） 模型

1.1 传统GM（1，1）

GM（1，1） 建模的原理和条件为：原始数据要具有准光滑性，且累积的数据要具有准指数规律；因此，在利用灰色理论解决问题之前，需要进行建模可行性分析[6]。可设非负原始序列为：X（0）={x（0）（1），x（0）（2），…，x（0）（n）}，该序列是由埋地管道腐蚀深度检测值组成的一组序列。为减弱原始序列随机性，对X（0）进行一阶累加得到X（1）={x（1）（1），x（1）（2），…，x（1）（n）}，其中 x（1）（k）=，k=1，2，…，n。

采用光滑比ρ作准光滑性检验：

式中：ρ（k）为第k次检验的光滑比。当k＞3时，如ρ（k）＜0.5，则埋地管道腐蚀深度检测值组成的序列为准光滑序列。

采用级比σ作准指数规律检验：

式中：σ（k）为第k次检验的级比。当k＞3时，如σ（k）∈[g，h]，且h-g＜0.5，则埋地管道腐蚀深度检测值组成的累加序列为准指数序列。

将X（1）作紧邻均值生成处理，得到紧邻生成序列：Z（1）=｛z（1）（2），z（1）（3），…，z（1）（n）｝。

其中：

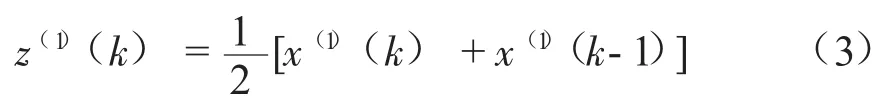
建立GM（1，1）模型的灰色微分方程：

将式（4）变形为白化微分方程：

式中：a为发展系数，反映控制系统的发展态势；b为灰色作用量，反映数据变化的关系。a和b采用最小二乘法计算。

在初始条件 x（0）（1） =x（2）（1） 时，GM （1，1）模型的时间响应序列为：

对式（6）进行累减还原：

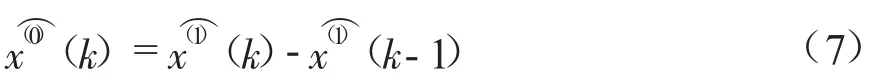
1.2 IGM （1，1）

根据式（6） 和式（7） 可知，GM（1，1）预测结果的准确性与a、b的取值有关，而根据最小二乘法计算 a、b 取值与 z（1）（k） 密切相关[7]。因此背景值z（1）（k） 是影响GM（1，1） 模型精度的重要因素。对式（5） 在区间[k-1，k]进行积分：

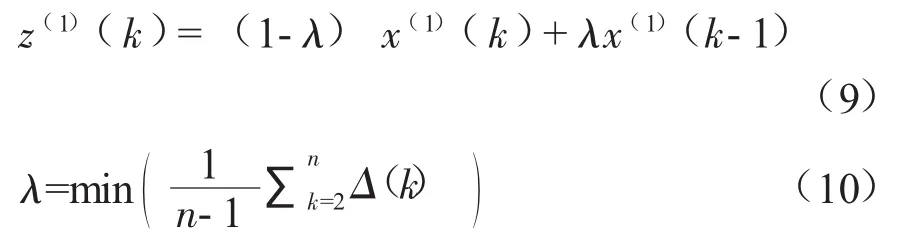
式中：Δ（k）为相对残差序列。

优化条件是通过选取合适的步长，将实际值和模型预测值之间的平均相对误差最小作为约束条件选取可变权参数λ，用于降低背景值的计算误差。

此外，随着内外环境的不断变化，埋地管道的腐蚀趋势也处于变化中，由式（6）可知，拟合曲线经过第一个数据点，传统的GM（1，1） 模型只利用了旧数据，但对于埋地管道腐蚀深度而言，新数据往往更有意义。根据灰色系统新信息优先的原则，采用 x（1）（n） 代替 x（0）（1），此时 x（1）（n）为累加数据，原始序列中的每一个数值均在x（1）（n）中得到体现，且n的不断变化体现了新信息的不断更新，也解决了传统模型中预测值与x（0）（1） 无关的问题，形成新陈代谢的GM（1，1）模型：

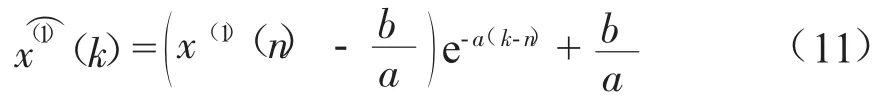
2 WOA-SVM模型

SVM支持向量机模型以统计学VC理论和结构风险最小化为基础，可用于处理小样本数据的非线性分类和回归问题。本文涉及回归问题，基本思想是将数据集通过一个非线性映射将低维空间转换为高维空间，然后在高维空间对数据集进行回归拟合。此外，该方法可通过核函数将高维空间中的运算转换为原样本空间，降低高维运算的复杂性，缩短样本训练和预测的时间。由于埋地管道的腐蚀数据检测周期较长，获取的数据量有限，故SVM模型适合在数据少、信息贫的样本中使用。SVM模型的回归函数f（x） 为：

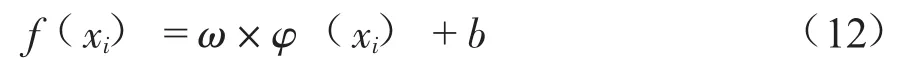
式中：xi为数据集 （x1，x2，…，xn），φ（xi)为非线性映射函数，n为样本数据个数，ω和b均为回归因子。

根据多元统计分析理论，通过以下目标数的极小化确定SVM回归函数：

约束条件为：

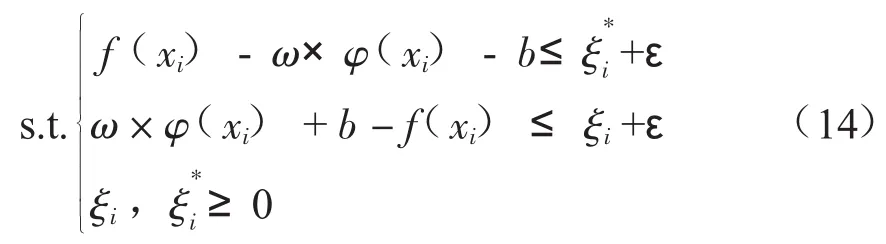
式中：C为惩罚变量，ε为不敏感损失函数的参数，ξi和为松弛变量。

引入拉格朗日函数，将上述优化问题转为对偶性变量问题，并选用径向基核函数，得到：

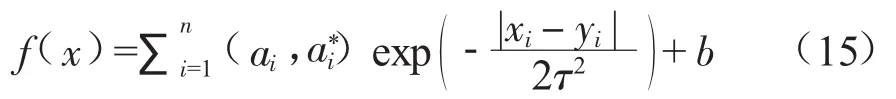
式中：ai和为拉格朗日乘子，为径向基核函数，τ为核函数宽度。

对于SVM模型，预测性能受惩罚变量C和核函数宽度τ两个参数的影响较大，在此采用WOA模型对参数进行优化，以提高SVM的回归性能。

WOA模型属于仿生学算法，原理是根据鲸鱼捕食过程：鲸鱼发现猎物后先潜入到猎物底部，随后沿着螺旋路径向上形成独特气泡，最终将猎物缩小在较小范围内吞食，整个过程分为收缩气泡、随机狩猎和螺旋狩猎3部分[8-9]。用参数A表示鲸鱼是通过收缩气泡还是随机狩猎来搜索猎物。

当|A|＜1时，在鲸鱼种群中选择位置最好的一头鲸鱼，其余鲸鱼向这个位置逐步靠近并包围猎物，位置更新公式如下：

式中：t为当前迭代次数；X*（t）为当前鲸鱼的最优位置向量；X（t）为当前鲸鱼的位置向量；A和C均为系数向量，定义如下：

式中：r为[0，1]之间的随机数；a经迭代后其值由2线性减小到0。

当|A|≥1时，在鲸鱼种群中随机选择一头鲸鱼位置Xrand为最优位置向量，用于更新其余鲸鱼的位置，位置更新公式如下：

当鲸鱼寻找到猎物时，针对猎物形成螺旋形运动轨迹捕获猎物。位置更新公式如下：

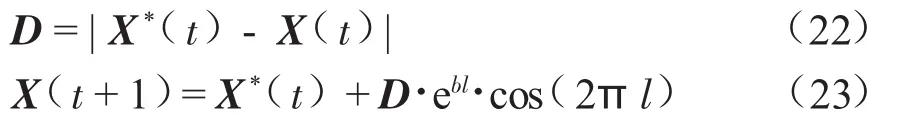
式中：b为常数，l为[-1，1]之间的随机数。

3 基于IGM-WOA-SVM的腐蚀深度预测模型

基于IGM所需数据较少和SVM可挖掘复杂系统退化信息的特点，建立IGM-WOA-SVM的腐蚀深度预测模型。管道腐蚀深度的变化是管材老化和环境随机变量相互影响的结果。管材老化可用灰色模型预测，而灰色模型预测值与实际值之间的差异可视为环境因素作用下的非线性数据行为，可用SVM模型进行非线性回归，形成误差补偿器。步骤如下：

（1）选取n组固定检测周期下的腐蚀深度数据作为原始序列，其中m组作为训练集，n-m组作为测试集，训练集的数据经IGM预测后得到灰色预测值。

4 实例分析

选取某区域X70管道进行研究，该管道外径340.8 mm、壁厚10.5 mm、最小屈服强度529 MPa、运行压力4 MPa，至今已服役10年，每半年进行一次腐蚀深度检测，根据所管理的部分历史记录及部分开挖检测数据，共获得20组腐蚀深度数据。

4.1 可行性分析

对20组数据进行累加处理后，根据式（1）和（2） 进行可行性分析。其中，ρ（3）、ρ（4） 均大于等于0.5，检测序次1～3的原始数据呈直线分布，可将其视为无限光滑序列，0.137 9≤ρ（5）～ρ（20）≤0.4000，满足ρ（k）＜0.5；1.1379≤σ（3）～σ（20） ≤1.5000，满足h-g=1.5000-1.139 7=0.360 3＜0.5。因此，检测值构成的序列为准光滑序列且累加生成的序列具有准指数规律，可以利用GM（1，1） 建模。

4.2 IGM（1，1） 预测

采用传统的GM（1，1） 模型进行预测，得到发展系数a=-0.127 0，灰色作用量b=0.038 8，根据式（6）得到腐蚀深度的时间响应序列为：

利用式（7）进行累减还原，即可得到如表1所示的GM（1，1） 预测结果。可知GM模型在不同阶段的预测精度差别较大，其中第14次的预测值与实际值基本重合，而其余时刻的相对误差较大，最大相对误差为150.35%，平均相对误差为25.03%，不满足精度要求。

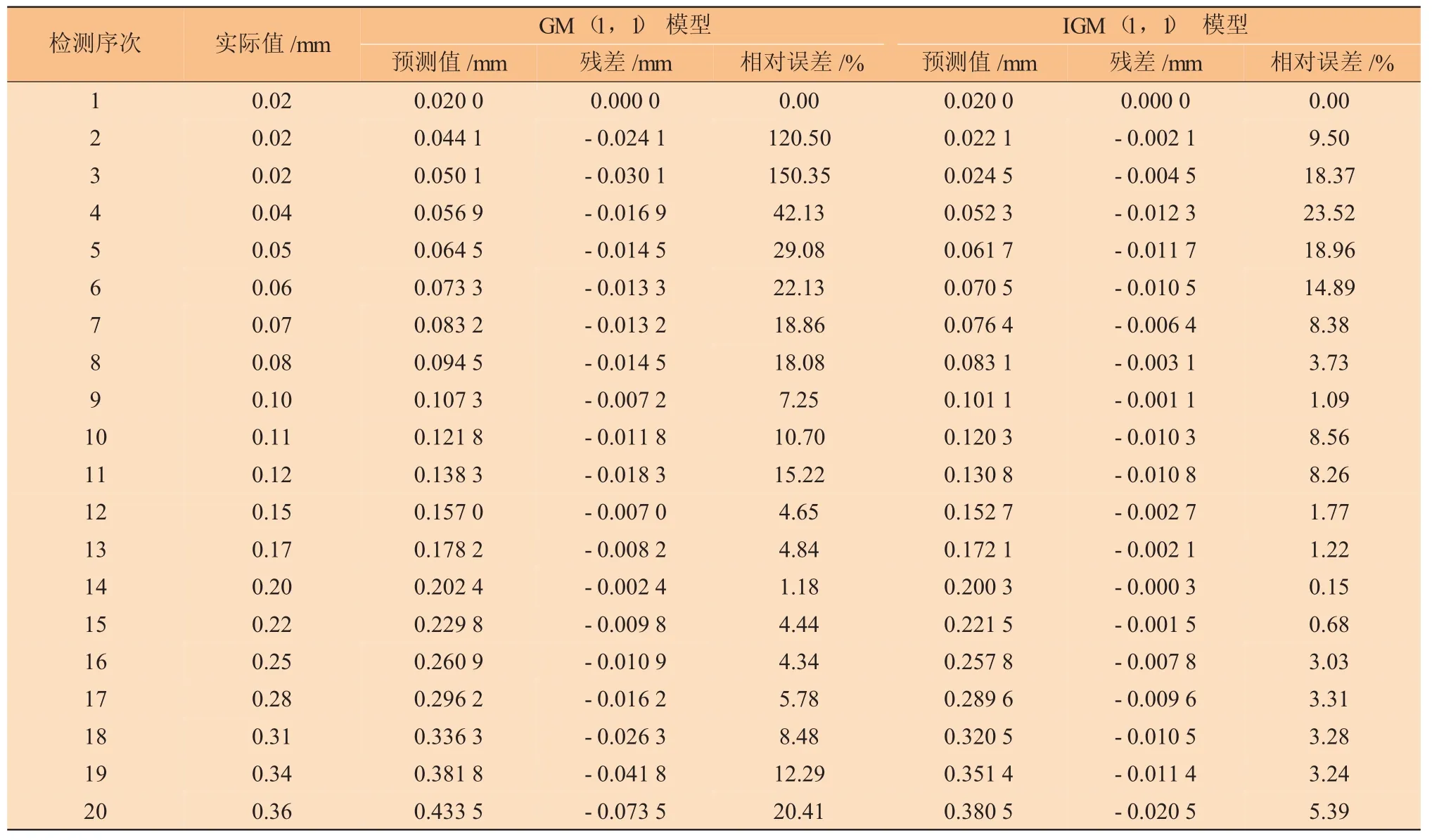
表1 GM（1，1）和IGM（1，1）的预测值结果对比

考虑到灰色系统新信息优先和最少信息原则，对背景值和初始值进行改进，形成IGM（1，1）模型，得到发展系数a=-0.121 5，灰色作用量b=0.059 3，根据式（11）得到腐蚀深度的时间响应序列为：

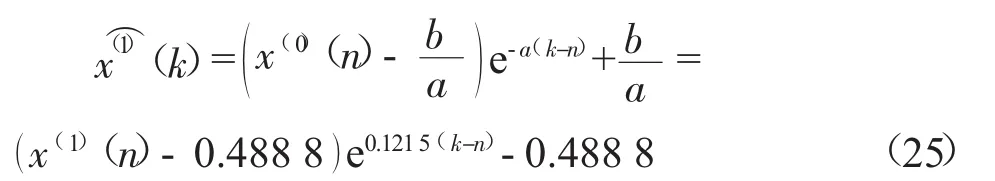
利用式（7）进行累减还原，即可得到如表1所示的IGM（1，1） 预测结果。由表1可知：IGM（1，1）模型的拟合精度与传统GM（1，1）模型相比有很大提升，最大相对误差为23.52%，平均相对误差为6.86%，且IGM（1，1）发展系数的绝对值较小（发展系数越小，预测范围越大，精度越高），说明IGM（1，1） 模型不仅适合短期预测，同样适合中、长期预测，也证实了腐蚀深度的动态变化和新数据优先对预测的重要性。

4.3 WOA-SVM误差补偿器

为了验证WOA算法的优越性，分别选择GA（遗传算法）[10]、PSO（粒子群算法）[11]、FOA（果蝇优化算法）[12]进行对比，其中GA交叉因子取0.8，变异因子取0.05；PSO学习因子取1.5，惯性权重取0.2，粒子维数取1；FOA的遗传代数为200；WOA的种群数量为20，迭代次数100次，选用5折交叉验证，以均方根误差和相关系数作为优选标准，对SVM模型中的C和τ参数进行优选，结果见表2。

表2 C和τ参数优选结果

4种算法的均方根误差均较小，其中WOA的均方根误差比其余3种算法小一个数量级；WOA的相关系数最大，为0.991 5；同时，WOA算法在迭代的过程中均方根误差在前、中、后期均有所波动，说明WOA算法可避免陷入局部最优，该算法可适用于基于SVM的腐蚀深度预测。

将表1中的IGM（1，1） 的预测结果作为WOA-SVM模型的输入变量，将残差序列作为输出变量，取1～12检测序次的数据为训练集，13～20检测序次的数据为测试集，在Matlab工具箱中进行训练。测试集的预测结果如表3所示。

表3 残差序列预测结果

将训练集和测试集的残差预测值与IGM（1，1）的预测结果相加，得到最优输出值，见图1。IGM（1，1） 模型和IGM-WOA-SVM模型的相对误差见图2。

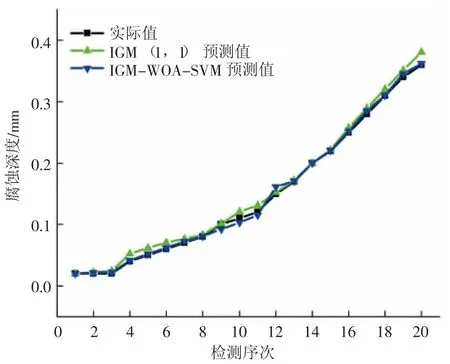
图1 预测结果对比

图2 相对误差对比

IGM-WOA-SVM模型比IGM（1，1） 模型的预测精度更高，除第10组和第12组预测误差较大外，其余组的相对误差均在5%以内，平均相对误差1.21%，与实际值的拟合效果较好。参照文献[13]，分别计算GM（1，1） 模型、IGM（1，1）模型和IGM-WOA-SVM模型的后验差比和小误差概率。3种模型的后验差比分别为0.45、0.08、0.05，小误差概率分别为0.85、0.95、1，预测精度等级分别为合格、好、好，IGM-WOA-SVM模型的预测精度最好。这是由于SVM模型具有较强的非线性逼近能力及训练能力，对影响管道腐蚀深度变化的随机变量进行了定量化处理，在腐蚀深度预测上进行了补偿，使预测结果更加准确。

4.4 剩余寿命计算

根据AMSE B31G—2009的相关要求，计算管道的最大腐蚀深度为7.50 mm，即管道的极限腐蚀深度为7.50 mm。采用IGM-WOA-SVM模型预测第20次以后检测的腐蚀深度，见图3。第42次检测时，管道腐蚀深度预测值为6.89 mm，第43次检测时，管道腐蚀深度预测值为7.53 mm，因此在第42次检测后，应及时对管道进行维修或换管处理，防止腐蚀穿孔发生，得到剩余寿命为11年。

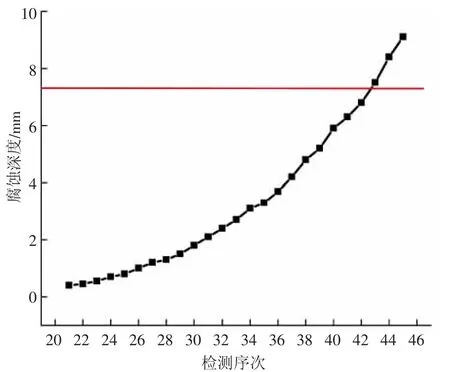
图3 腐蚀深度发展趋势

5 结论与建议

（1） 对GM（1，1） 模型的背景值和初始值进行改进，形成IGM（1，1） 模型，预测准确性大幅提高，预测结果的平均相对误差为6.86%。

（2） 训练WOA-SVM模型为误差补偿器，IGM-WOA-SVM模型预测结果的平均相对误差为1.21%，该模型对于管道腐蚀深度的预测具有很好的适用性。

（3）管道除受到腐蚀影响外，还受其余载荷应力的影响，今后应综合考虑多方面因素，完善预测模型。