一类3线缠绕的染色数

王树新， 王 一， 葛 悦， 杜 怡

(辽宁师范大学 数学学院，辽宁 大连 116029)

20世纪纽结和链环理论作为低维拓扑学的一个重要组成部分快速地发展起来，寻找纽结和链环强有力的合痕不变量，一直都是纽结和链环理论研究的一个重要课题. 1970年，J. H. Conway给出了有理缠绕连分数的定义并实现对有理缠绕的分类[1]；2004年，L. H. Kauffman和S. Lambropoulou不仅给出了缠绕的染色规则，而且证明了在此规则下的染色分数是一个同痕不变量[2]；2019年,卢硕在有理缠绕染色的基础上，讨论了两类代数缠绕染色的性质[3]；2020年,王冬雪等讨论了有理缠绕染色矩阵的性质，将2线缠绕的染色问题推广到n线缠绕的染色问题，并研究了一类n线缠绕的染色性质[4-5].

本文从上述研究结果出发，对缠绕染色进行进一步的研究，将2线缠绕的染色与3线缠绕的染色紧密地结合起来，对一类3线缠绕染色进行细致的研究和分析，给出了上述3线缠绕的一种特定染色，在此基础上，确定了相应3线缠绕的染色数. 本文得到的一类3线缠绕染色数及其染色性质，为进一步的研究广义缠绕以及更一般的多线缠绕的染色性质和分类提供了一种新的研究思路，同时也对纽结和链环的分类起到了积极的促进作用.

1 预备知识

定义1设(B,t)是一个偶对，若B是一个三维实心球体，t是真嵌入B中的有限条、非定向的互不相交的弧段，则称(B,t)为一个缠绕，若t=t1∪t2，则称(B,t)为一个2线缠绕.

注1本文不特加说明，一般用大写字母T或Ti(i∈+)表示缠绕.

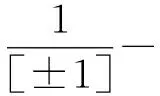
定义4设T1，T2是两个缠绕，如图1所示，将T1的NE端与T2的NW端相连接，T1的SE端和T2的SW端相连接，称上述操作为缠绕T1和T2的加法，记所得缠绕为T1+T2，如图1(a)所示.把T1的SW端和T2的NW端相连接，把T1的SE端和T2的NE端相连接，称上述操作为缠绕T1和T2的乘法，记所得缠绕为T1*T2，如图1(b)所示.

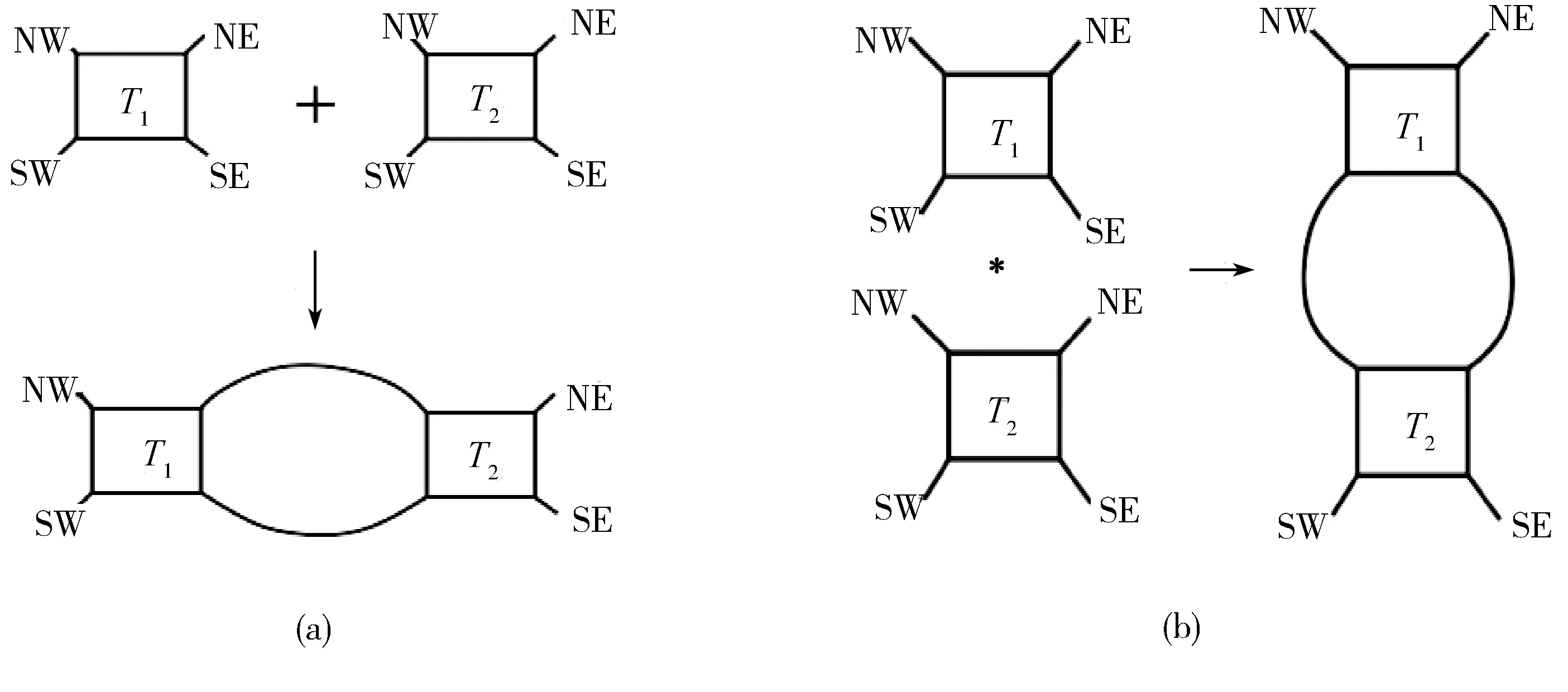
图1 缠绕T1和T2加法和缠绕T1和T2乘法Fig.1 The addition and multiplication of tangles T1and T2

定义5设T为一个缠绕，在T中任选一个交叉点，上弧段标记整数β，两条下弧段分别标记整数α和γ，使得α，β，γ满足2β=α+γ，其中，α≠γ，若T的每个交叉点对应的弧段均保持上述染色规则，且相连的弧段不出现矛盾，则称T为一个染色缠绕.

图2给出了某一缠绕特定交叉点的局部染色规则.

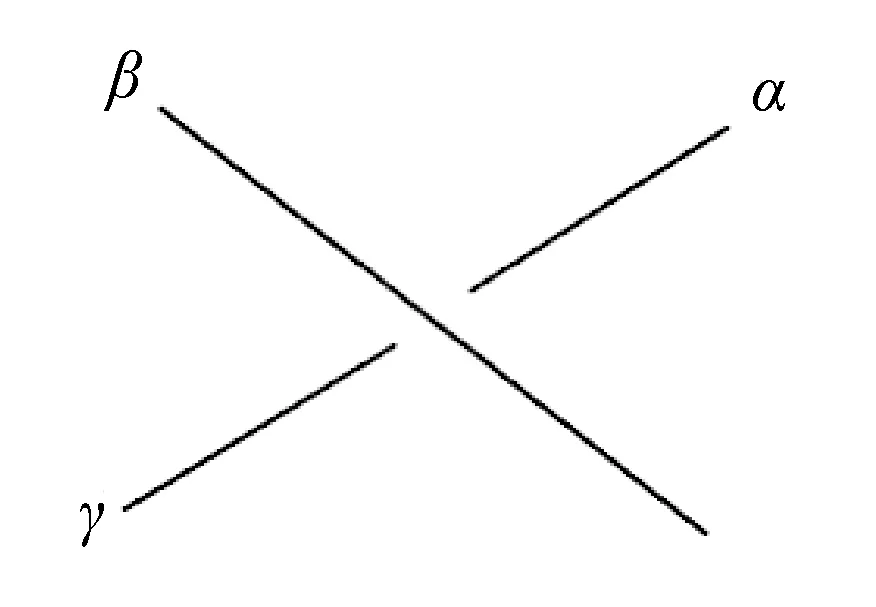
图2 缠绕交叉点的局部染色规则Fig.2 The coloring rule of local crossing of tangle

定义7设T1，T2，T3，…，Tn(n∈+)均为整数缠绕，若缠绕T是由T1，T2，T3，…，Tn按照如图3所示的完全非代数连接方式构造得到，则称T是一个完全非代数连接3线缠绕.

注3若横向观察图3中3线缠绕，易知此3线缠绕是由两行整数缠绕按照完全非代数连接方式得到的.本文仅研究定义7中给出缠绕的染色数.

图3 一类3线缠绕T的构造方式Fig.3 Constructions of a class of 3-tangle T

定义8设T为一个缠绕，DT是缠绕T的任意一个投影图，对DT进行染色，记C*(DT)是相应染色所需不同染色整数的个数，称C**(T)=min{C*(DT)|DT为缠绕T的任意一个投影图}为缠绕T的染色数.

命题1设T是一个如图4所示的3线缠绕，则C**(T)=5.

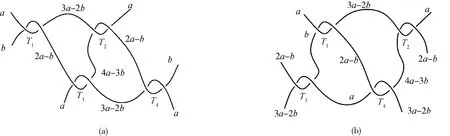
图4 3线缠绕TFig.4 3-tangle T

注4利用缠绕染色规则，命题1的证明参见文献[6]中的命题2.1.1和命题2.1.2，并且图4中给出了相应弧段对应的染色整数，其中,a,b,2a-b,3a-2b,4a-3b是互不相同的整数.

2 主要结果

定理1设Ti是一个[2]-缠绕(i=1,2,…,n)，若缠绕T由Ti(i=1,2,…,n)按图5所示连接得到，则C**(T)=5.

图5 3线缠绕TFig.5 3-tangle T

证如图5所示，缠绕T的子缠绕Ti(i=1,2,…,n)可分为两行，将缠绕T的左端看作始端，右端看作末端，则缠绕T的始端子缠绕T1所在位置有两种情况，下面分情况讨论.

(1)子缠绕T1在第一行

子缠绕T1在第一行时，按图4(a)中染色数为5的染色方式为缠绕T染色，并从缠绕T的始端出发，按图4(a)所示的缠绕染色形式对缠绕T进行分组直至末端，其分组情况与子缠绕个数有关，下面分情况讨论.

(a)n=4m

如图6所示沿虚线将缠绕T按图4(a)的缠绕形式进行分组，若n=4m，则缠绕分为若干组后，不存在剩余[2]-缠绕.由命题1可知，每组缠绕染色数为5且每组相应的染色数相同，故C**(T)=5.

图6 缠绕T的分组和染色Fig.6 Grouping and coloring of tangle T

(b)n=4m+1

如图7所示沿虚线将缠绕T按图4(a)的缠绕形式进行分组，若n=4m+1，则缠绕分为若干组后，有一个剩余[2]-缠绕Tn.由命题1可知，每组缠绕染色数为5且每组相应的染色数相同，再由缠绕染色规则，子缠绕Tn中不出现新的染色整数，故C**(T)=5.

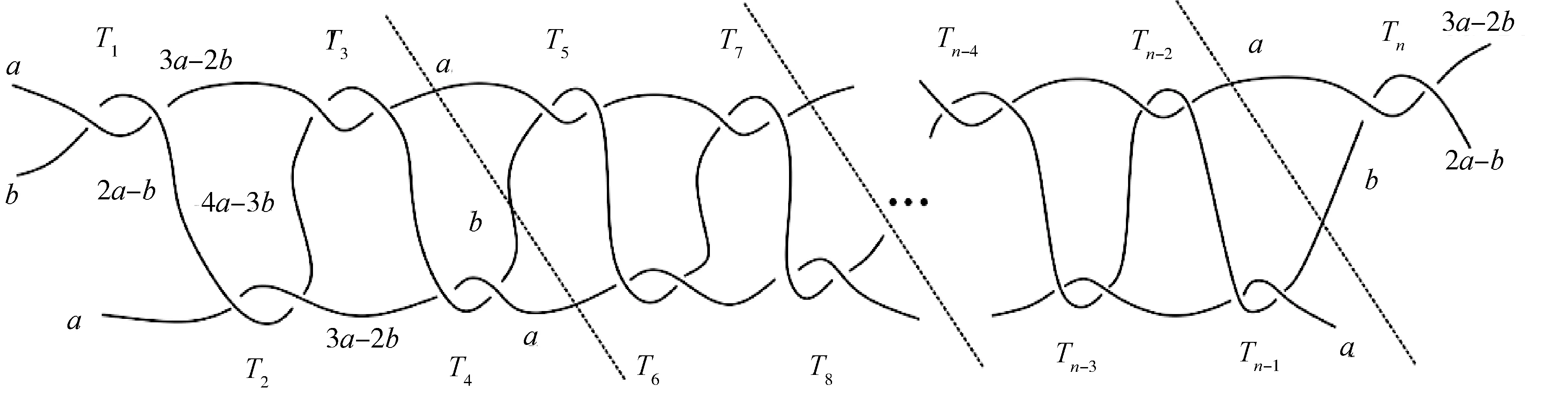
图7 缠绕T的分组和染色Fig.7 Grouping and coloring of tangle T

(c)n=4m+2

如图8所示沿虚线将缠绕T按图4(a)的缠绕形式进行分组，若n=4m+2，则缠绕分为若干组后，有两个剩余[2]-缠绕Tn-1，Tn.由命题1可知，每组缠绕染色数为5且每组相应的染色数相同，再由缠绕染色规则，子缠绕Tn-1，Tn中不出现新的染色整数，故C**(T)=5.

图8 缠绕T的分组和染色Fig.8 Grouping and coloring of tangle T

(d)n=4m+3

如图9所示沿虚线将缠绕T按图4(a)的缠绕形式进行分组，若n=4m+3，则缠绕分为若干组后，有3个剩余[2]-缠绕Tn-2，Tn-1，Tn.由命题1可知，每组缠绕染色数为5且每组相应的染色数相同，再由缠绕染色规则，子缠绕Tn-2，Tn-1，Tn中不出现新的染色整数，故C**(T)=5.

图9 缠绕T的分组和染色Fig.9 Grouping and coloring of tangle T

(2)子缠绕T1在第二行

子缠绕T1在第二行时，按图4(b)中染色数为5的染色方式为缠绕T染色，并从缠绕T的始端出发，按图4(b)所示的缠绕形式对缠绕T进行分组直至末端，其分组情况与子缠绕个数有关，下面分情况讨论.

(a)n=4m

如图10所示沿虚线将缠绕T按图4(b)的缠绕形式进行分组，若n=4m，则缠绕分为若干组后，不存在剩余[2]-缠绕.由命题1可知，每组缠绕染色数为5且每组相应的染色数相同，故C**(T)=5.

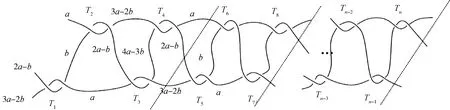
图10 缠绕T的分组和染色Fig.10 Grouping and coloring of tangle T

(b)n=4m+1

如图11所示沿虚线将缠绕T按图4(b)的缠绕形式进行分组，若n=4m+1，则缠绕分为若干组后，剩余一个[2]-缠绕Tn.由命题1可知，每组缠绕染色数为5且每组相应的染色数相同，再由缠绕染色规则，子缠绕Tn中不出现新的染色整数，故C**(T)=5.

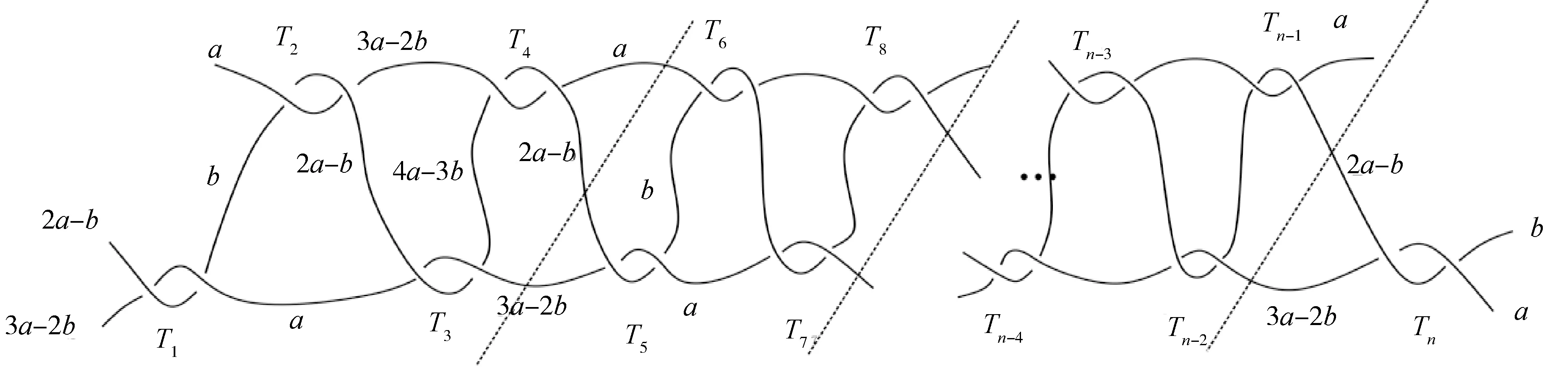
图11 缠绕T的分组和染色Fig.11 Grouping and coloring of tangle T

(c)n=4m+2

如图12所示沿虚线将缠绕T按图4(b)的缠绕形式进行分组，若n=4m+2，则缠绕分为若干组后，剩余两个[2]-缠绕Tn-1，Tn.由命题1可知，每组缠绕染色数为5且每组相应的染色数相同，再由缠绕染色规则，子缠绕Tn-1，Tn中不出现新的染色整数，故C**(T)=5.

图12 缠绕T的分组和染色Fig.12 Grouping and coloring of tangle T

(d)n=4m+3

如图13所示沿虚线将缠绕T按图4(b)的缠绕形式进行分组，若n=4m+3，则缠绕分为若干组后，剩余3个[2]-缠绕Tn-2，Tn-1，Tn.由命题1可知，每组缠绕染色数为5且每组相应的染色数相同，故C**(T)=5.

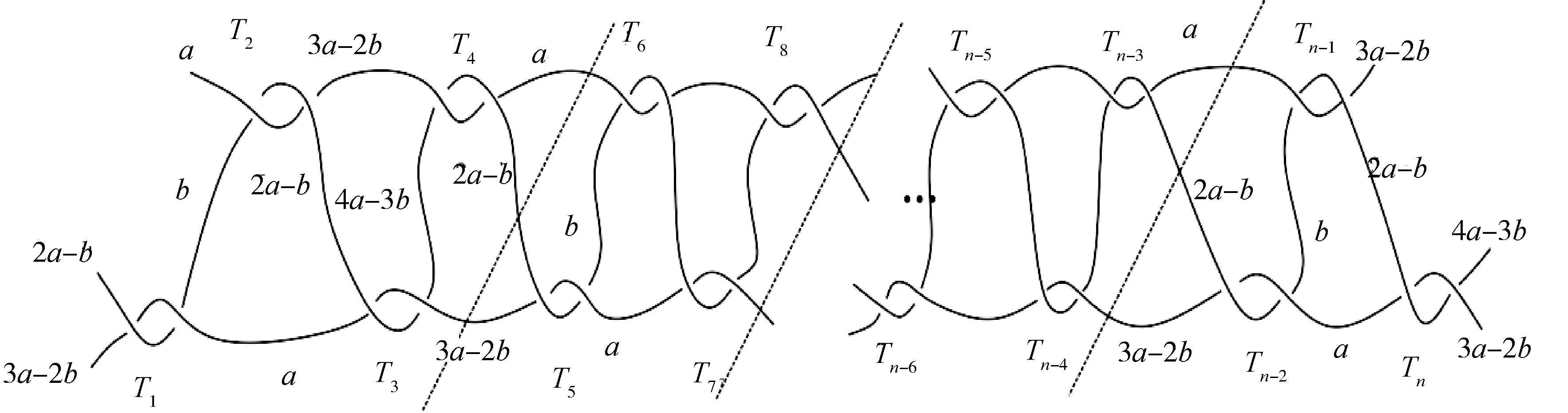
图13 缠绕T的分组和染色Fig.13 Grouping and coloring of tangle T

综上所述，C**(T)=5.