基于空间模型的绗缝因素对羽绒制品保暖性的影响
2022-01-10代萌婷屠晔
代萌婷, 屠晔
(1.浙江理工大学 服装学院,浙江 杭州 310018;2.浙江理工大学 国际教育学院,浙江 杭州 310018)
绗缝是羽绒制品生产过程中一道重要的工序,可以起到固定羽绒绒朵,增加保暖性的效果[1-2]。在绗缝因素研究中,绗缝形式与绗缝数量对羽绒制品的保暖性有重要的影响,但此类研究多是在水平放置状态下测试保暖性。水平放置与服装日常使用状态存在较大差异[3-4],在实际穿着中服装与地面呈垂直状态,当绗缝间距较大时重力作用会影响羽绒绒朵分布,导致保暖性下降[5-6]。目前,放置状态、绗缝因素与羽绒保暖性的关系尚不明确。因此,有必要以定量分析的方式探究不同的放置状态、绗缝因素与羽绒保暖性的关系。
文中在分析是否悬挂放置及放置时间对羽绒保暖性影响的基础上,设计双因素实验,结合绗缝形式与绗缝数量测试两种放置状态下羽绒的保暖性,同时建立羽绒表观体积近似几何模型,定量分析和预测羽绒的保暖性。以期为羽绒服类产品的绗缝因素设计和开发提供参考。
1 材料与方法
1.1 原料与仪器
1.1.1原料 羽绒服面料(100 %涤纶织物,面密度102 g/m2),防绒内胆(100 %涤纶织物,面密度76 g/m2),均由苏州纺织公司生产;白鹅绒(纯度95%),由山东奥绒服装公司生产。
1.1.2仪器 YG606D型纺织品保暖测试仪,宁波纺织仪器厂制造;游标卡尺,上海耐美特实业有限公司制造;恒温恒湿实验室,中山科瓦特机电有限公司制造;试样悬挂装置,自制,具体如图1所示。
图1 悬挂装置Fig.1 Suspension device
1.2 方法
1.2.1实验因素与水平的确定 由于绗缝形式与绗缝数量对羽绒制品的保暖性有重要的影响,故将绗缝形式和绗缝数量作为实验因素。绗缝形式包括直线、折线、曲线3种,而直线绗缝居多。文中选用直线绗缝,将绗缝形式设置为水平绗缝、垂直交叉绗缝、斜线绗缝3个水平。不同的绗缝数量会影响羽绒试样静止空气的含量,进而影响保暖性,故绗缝数量设置为0~6条共7个水平。
1.2.2试样制备 将羽绒服原材料制作成30 cm×30 cm的试样,其中,白鹅绒的填充密度选择130 g/m2[7]。将不同绗缝形式、绗缝数量组合可以得到19个试样,编号为0#~18#,具体如图2所示。

图2 不同水平组合下的绗缝试样Fig.2 Quilted samples with different combinations
1.2.3悬挂放置时间的选定 受重力的影响,试样悬挂一定时间后,部分羽绒会下沉。为了探究悬挂放置时间对羽绒保暖性的影响,采用0#试样进行悬挂放置实验,放置时间分别为0,1.5,3.0,6.0,12.0,18.0,24.0 h,测试其保暖性,同时与水平放置方式进行对比,具体结果如图3所示。
由图3可以看出,悬挂状态下,0#试样的传热系数先随着悬挂时间的增加而增大,随后变化趋于平缓;当悬挂放置时间在18~24 h之间,试样传热系数不再发生变化,达到稳定状态;在水平放置状态下,0#试样的传热系数不受时间的影响。因此,以下实验悬挂放置时间取24 h。

图3 0#试样传热系数随放置时间变化的趋势Fig.3 Trend of 0#sample's heat transfer coefficient over time
1.2.4试样保暖性的测试 在温度(20±2)℃、相对湿度65%±2%的条件下,根据GB/T 35762—2017《纺织品热传递性能试验方法平板法》[8],采用纺织品保暖测试仪测试水平放置与24 h悬挂放置试样的传热系数。每个试样重复测量3次,取平均值。
1.2.5试样缝边长度的测试 采用游标卡尺测量试样缝边a,b的长度,其中,a为绗缝数量较少的边,b为绗缝数量较多的边。每个试样重复测量3次,取平均值。
2 结果与分析
试样缝边长度测试结果见表1。

表1 试样保暖性及缝边长度测试结果
2.1 绗缝形式和绗缝数量对羽绒保暖性的影响
2.1.1两种放置方式下羽绒保暖性分析 将绗缝形式、绗缝数量和放置方式作为控制变量,试样传热系数作为因变量,采用方差分析方法探究变量之间的主效应与交互效应,得到主体间效应检验结果,具体见表2。

表2 主体间效应检验
由表2可以看出,在显著水平α=0.05下,绗缝形式、绗缝数量与放置方式对试样传热系数均有显著影响;交互作用中绗缝数量×放置方式对试样传热系数的影响显著,绗缝形式×绗缝数量、绗缝形式×放置方式对试样传热系数的影响不显著。比较绗缝形式、绗缝数量、放置方式的概率p值,从低到高依次为绗缝数量<绗缝形式<放置方式,表明各因素对试样传热系数的影响程度由高到低依次为绗缝数量>绗缝形式>放置方式。
1)绗缝形式。分别对两种放置方式下3种绗缝形式试样的传热系数进行Duncan多重比较,具体结果见表3。

表3 不同绗缝形式的试样传热系数Duncan多重比较
由表3可以看出,3种绗缝形式的试样传热系数均值从小到大依次为斜线绗缝<水平绗缝<垂直交叉绗缝,表明不同绗缝形式试样的保暖性由强到弱依次为斜线绗缝>水平绗缝>垂直交叉绗缝。从直观上来看,在绗缝数量相同时,虽然斜线绗缝与水平绗缝分割的独立空间数量相同,但斜线绗缝分割出独立空间的两对立边宽度大,静止空气减少量较少;垂直交叉绗缝分割的独立空间数量比其他绗缝更密集,各绗线间的交叉点多,从而影响分割空间四角的厚度,静止空气减少量较多。
2)绗缝数量。分别对两种放置方式下的不同绗缝数量的试样传热系数进行Duncan多重比较,具体结果见表4。
由表4可见,在水平放置时,试样传热系数均值随绗缝数量的增加呈递增趋势,绗缝数量为0时试样传热系数均值最低;在悬挂放置24 h时,试样传热系数均值随绗缝数量的增加呈先减后增的趋势,绗缝数量为2条时试样传热系数均值最低。这是由于绗缝数量较少时,试样内羽绒有足够的空间距离,可阻碍绒朵间相互抱合,纤维热传导降低,内部空气流动阻力增大,对流传热微弱,保暖性较好。当绗缝数量增加后,试样被分割成多个独立空间,绒朵间相互接触增加纤维的热传导[9-10],且每个独立空间边缘处空气流动阻力变小,对流传热增加,保暖性下降。

表4 不同绗缝数量的试样传热系数Duncan多重比较
3)处理方式。对两种放置方式下试样的传热系数进行配对样本T检验。在显著水平α=0.05下,两种放置方式下试样的传热系数有显著性差异。由图5可知,水平放置状态下测得的试样传热系数低于24 h悬挂放置的,试样传热系数差值在绗缝数量为0~2条时急剧下降,随着绗缝数量继续增加试样传热系数差值逐渐减小并趋于相同。这是由于绗缝数量为0~2条时,绗缝对羽绒绒朵的固定作用较弱,部分羽绒绒朵受到重力作用产生竖直方向的位移,造成位移处两层面料之间没有羽绒三维结构的支撑[11-12],面料与外界环境产生热对流[13],所以此时试样悬挂放置对羽绒保暖性有显著影响;当绗缝数量增加至4条后,分割空间随之减小,迫使绒朵在每个独立空间内活动间隙减小,绗缝对羽绒的固定作用增强,故此时试样悬挂放置对羽绒保暖性影响较小。因此,为确保羽绒制品实际穿着时的保暖效果,绗缝数量至少为2条。
2.1.2两种放置方式下羽绒保暖性关系 从2.1.1可知,当绗缝数量≥2条时,水平放置与24 h悬挂放置的羽绒试样内部状态均达到稳定状态,在此基础上建立两种放置方式下羽绒试样保暖性回归模型,即
y=0.942 7x+0.200 3,R2=0.998。
其中,x,y分别为水平放置和24 h悬挂放置试样的传热系数[W/(m2·℃)]。
两种放置方式下试样保暖性线性拟合曲线如图4所示。由图4可知,在绗缝数量≥2条时,两种放置方式下试样的传热系数呈高度线性相关,回归模型预测精度达到0.998,表明回归模型拟合效果较优。

图4 两种放置方式下羽绒试样保暖性线性拟合结果Fig.4 Linear fitting results of two kinds of placement treatment of down
2.1.3绗缝形式及绗缝数量与羽绒保暖性的关系 为了探究绗缝形式、绗缝数量和水平放置方式与试样传热系数的关系,根据表1测试数据,选用虚拟变量方式对三者关系进行拟合。 虚拟变量是反映质的属性的人工变量,通常取0或1,使用虚拟变量可增加模型精度, 降低误差方差。 将水平放置试样传热系数作为因变量,绗缝形式与绗缝数量作为自变量,绗缝数量设为n,水平绗缝、垂直交叉绗缝、斜线绗缝的虚拟变量分别设为(Z1=0,Z2=1)(Z1=1,Z2=0)(Z1=0,Z2=0),利用SPSS软件得到虚拟变量模型,具体见表5。由表5可知,模型R2=0.968,表明模型拟合度良好。不同绗缝形式下绗缝数量与水平放置试样传热系数拟合方程为

表5 模型汇总
水平绗缝x=1.857+0.232n;
垂直交叉绗缝x=1.919+0.232n;
斜线绗缝x=1.713+0.232n。
式中,x为水平放置试样的传热系数[W/(m2·℃)]。
2.2 试样表观体积对羽绒保暖性的影响
为了进一步对绗缝因素和试样保暖性关系进行定量分析,以水平绗缝为例,建立绗缝后试样表观体积的近似几何模型,分析绗缝因素对水平放置试样保暖性的影响。
2.2.1试样表观体积近似几何模型 水平绗缝三维示意如图5所示。x-z截面示意如图6所示。
由图5可以看出,水平绗缝试样表观体积可近似视为若干个均匀椭圆柱体体积之和。记绗缝后两相邻边长度为a,b,椭圆柱体的椭圆截面面积为Sε,由A,B,D,A构成的截面面积为Sδ,单个椭圆柱体体积为VCE,水平绗缝试样表观体积为VH。
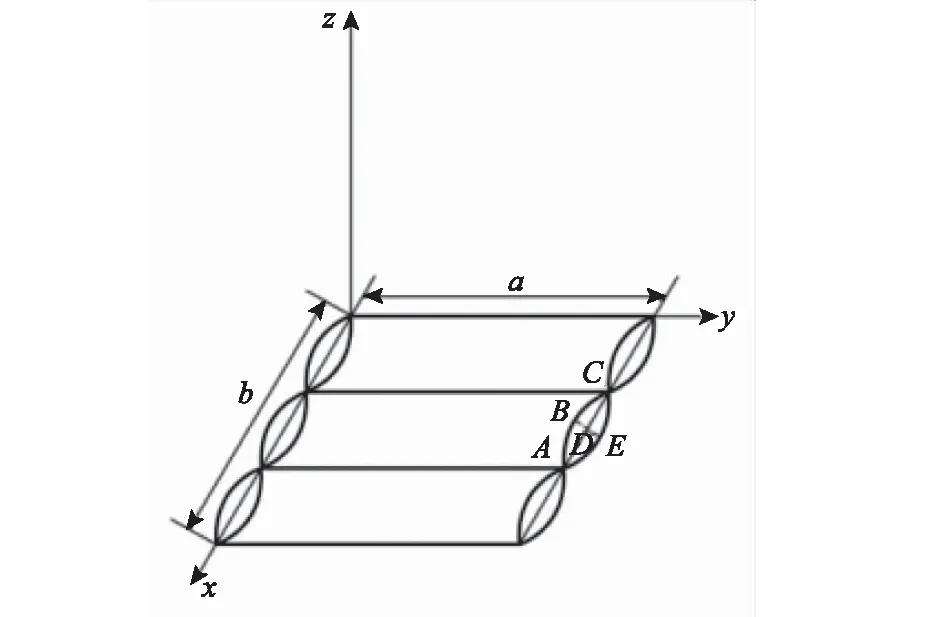
图5 n=2时水平绗缝三维示意Fig.5 3D schematic diagram of gorizontal quilting
根据图6及已知条件有:当绗缝数量为n时,椭圆柱体数量与绗缝数量的关系为n+1。

图6 椭圆柱体截面几何示意 Fig.6 Geometrical diagram of elliptical cylinder section
(1)
(2)
(3)
(4)
(5)
式中:l为试样长度(l=30 cm);n为绗缝数量;a,b为绗缝后两相邻缝边实际测量值;c为弧长;θ为弧长c对应的圆心角;r为圆柱体截面半径。
由于Sε不是完全的椭圆形,为精确模拟效果,采用差值法[14]计算Sε。

(6)
(7)
(8)
2.2.2试样表观体积与羽绒保暖性的关系 水平绗缝试样表观体积近似几何模型计算结果见表6。

表6 试样表观体积计算结果与传热导数的比较
由表6可知,试样的表观体积随绗缝数量的增加而减小,水平放置试样的传热系数随表观体积的增大而减小,表明此类试样保暖性随表观体积的增大而增加。对绗缝数量与试样表观体积的关系进行回归分析,在显著水平α=0.05下,回归模型显著性检验的概率p值小于显著水平(回归模型Sig=0.003 45、各系数分别为Sig=0.043 87,0.008 27,0.000 13),表明可建立回归模型。由此得到回归模型:
V=0.058n2-0.608n+2.352,R2=0.941。
式中:n为绗缝数量(条);V为试样表观体积(dm3)。
对水平放置试样的表观体积与传热系数的关系进行回归分析,在显著水平α=0.05下,回归模型显著性检验的概率p值小于显著水平(回归模型Sig=0.000 22,各系数分别为Sig=0.000 02,0.000 52,0.001 33),表明可建立回归模型。水平放置试样的表观体积与传热系数的回归模型:
x=0.784V2-3.333V+5.277,R2=0.985。
式中:x为水平放置试样的传热系数[W/(m2·℃)];V为试样表观体积(dm3)。
进一步对回归模型进行验证,结果见表7。
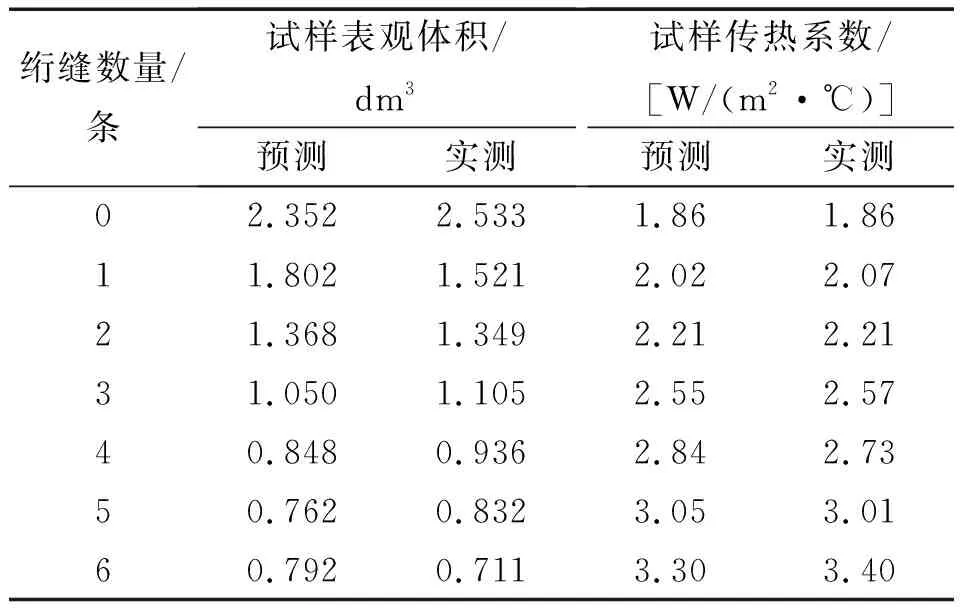
表7 试样表观体积和传热系数的测试结果比较
由表7可以看出,模型预测的传热系数分布在实测传热系数两侧且与实测数据接近,表明实测值与预测值相差较小,回归模型拟合度良好,可用该回归模型对羽绒的保暖性进行定量分析和预测。
3 结语
文中选取30 cm×30 cm羽绒试样,以水平绗缝、垂直交叉绗缝、斜线绗缝3种绗缝形式、 0~6条绗缝,在水平放置和24 h悬挂放置两种状态下,测试羽绒试样的传热系数,研究两种放置方式下绗缝形式与绗缝数量对羽绒保暖性的影响。同时建立绗缝后羽绒表观体积的近似几何模型,定量分析和预测羽绒制品的保暖性。研究表明:
1) 绗缝形式对羽绒保暖性影响显著,绗缝形式与处理方式交互作用不显著;3种绗缝形式的羽绒保暖性从高到低依次为斜线绗缝>水平绗缝>垂直交叉绗缝。
2) 绗缝数量对羽绒保暖性影响显著,绗缝数量与放置方式交互作用显著。水平放置时,羽绒保暖性随绗缝数量的增加呈递减的趋势;经过24 h悬挂放置,羽绒保暖性随绗缝数量的增加呈先增后减的趋势。
3) 两种放置方式下羽绒保暖性有显著差异。羽绒保暖性差值随绗缝数量的增加,呈先急剧下降、后缓慢下降并逐渐趋于相同的趋势。接近羽绒制品实际使用状况的24 h悬挂放置方式的较优绗缝数量为2条。
4) 当绗缝数量≥2条时,两种放置处理下羽绒保暖性呈高度线性相关,建立水平放置与24h悬挂放置的羽绒保暖性线性回归模型,模型预测精度可达到0.998。
5) 以水平绗缝为例,建立绗缝后羽绒表观体积的近似几何模型,羽绒表观体积随绗缝数量的增加而减小,羽绒保暖性随表观体积的增大而增加。并建立绗缝数量与羽绒表观体积、羽绒表观体积与保暖性的回归模型,回归模型可定量分析和预测羽绒制品的保暖性。
