基于有限元模型的上臂服装压位移影响因素分析

王贤君， 方丽英

(1.浙江理工大学 服装学院，浙江 杭州 310018；2.浙江理工大学 国际教育学院，浙江 杭州 310018)

目前，市场上有很多与手臂相关的针织紧身服装，如防晒袖、针织紧身护臂以及与医疗相关的医用压力袖套等。其中，针织运动护肘主要是提供适当压力以保护肘部关节的稳定，但与此同时也会对手臂其他部位产生较大的压力，尤其是上端口存在压力差的部位。针织运动护肘端口处的压力舒适性是影响产品舒适性的重要因素之一。针织运动护肘上端口对上臂施压，上臂会产生位移，从而引发人体压感的产生。1975年VERILLO R T[1]指出在理想的状态下，低于1 μm的位移就可以引起压力感觉的产生；覃蕊[2]在袜口压力研究中指出，人体受到的平均压力与平均位移存在极其显著的正相关性。因此，位移可以作为评价服装压感舒适性的指标。

目前，紧身服装压力舒适性研究主要围绕压力舒适阈值、压力和位移分布预测，以及主客观评价方法等方面。在压力与位移分布预测研究中，覃蕊等[2]运用有限元技术模拟穿袜子后脚踝的位移分布情况。李小欢[3]在压力臂套精确设计方法研究中建立了手臂有限元模型模拟压力臂套对臂部作用的服装压大小和分布，但没有考虑手臂形态的变化。多数学者只针对研究部位的单一状态进行压力舒适性分析，尹玲等[4]指出在相同环境下，同一个人穿同一个款式的服装，在静止和常规运动状态下，身体特定部位受到的压力和压感是不同的。陈晓娜等[5]在研究压缩式运动文胸对人体产生压力时，考虑了静态和动态对各个部位压力的影响，结果表明运动文胸的动态压力变化主要受人体运动周期影响。文中在此基础上运用有限元技术模拟上臂不同动作对上臂受压后位移分布的影响。

影响压力舒适性的因素主要有服装因素和人体因素[6]，文中重点考虑人体结构因素。人体上臂有肱二头肌和肱三头肌的存在，不同形态下的表面曲率差异较大，同时不同紧张程度的骨骼肌弹性模量是不同的，在同一维度的位移分布也会有变化。因此文中在研究上臂的位移分布时考虑上臂形态和肌肉弹性模量的变化，并分析位移与人体各结构因素的相关性，以期为服装压位移研究、舒适性的评价以及紧身服装的开发设计提供参考。

1 实验准备

1.1 接触位置的确定

针织护肘上端口和上臂的接触位置如图1所示。图1中将距肘部内测弯折点10～12 cm处定义为针织护肘上端口与上臂的接触位置(简称为接触位置，下同)。由于接触位置的上下两端臂围变化较小，为了适当简化模型，选取肘部沿大臂方向向上11 cm处的截面轮廓数据建立3D仿真模型。

图1 接触位置示意Fig.1 Schematic diagram of the contact position

1.2 实验对象的筛选

初选6位在校中等身材女大学生作为实验对象，各项指标满足以下要求；身高160～165 cm，臂围24～25 cm；最终经过筛选，取臂围最为接近臂围平均值的实验对象为建模对象，该实验对象年龄25岁，身高162 cm，体质量51 kg，臂围24.3 cm。

1.3 实验仪器

2NX-16型非接触式三维人体扫描仪，美国TC2公司制造；JK6113型皮脂厚度计，北京精凯达仪器有限公司制造。

2 人体数据的测量

2.1 三维扫描数据

采用非接触式三维人体扫描仪，要求受试者赤裸上肢，对其上肢伸直放松、弯曲放松、伸直紧绷、弯曲紧绷4种形态进行扫描，得到上肢点云数据，图2为上肢伸直放松状态下的人体点云图像。将上肢点云导入NX Imageware软件进行点云处理，得到上臂4种状态的外轮廓曲面。

图2 人体点云图Fig.2 Point cloud of the human body

2.2 截面数据

将上臂外轮廓曲面导入Solidworks 2018软件，用截面功能获取所需位置的截面，图3为上肢伸直放松状态下接触位置的截面轮廓。选取截面中心建立坐标系，其中0°方向为手臂的正前方，按照角度对截面进行区域划分，分割线与外轮廓相交得到16个分析点。使用曲率功能获得相应分析点的曲率。

图3 接触位置截面Fig.3 Sectional view of the contact position

2.3 皮脂数据

用皮质钳测量上臂各分析点的皮质厚度，4种状态下每个分析点测量3次，取平均值，最终确定16个分析点的皮质厚度。

3 接触位置模型的建立及有限元仿真模拟

3.1 接触位置3D模型的建立

上臂截面主要由皮肤、皮下脂肪、神经、血管、骨骼肌以及肱骨组成，其中皮下脂肪、神经、血管和骨骼肌统称为软组织。由于文中对骨骼肌单独建模，因此软组织部分的模型只包括皮下脂肪、神经和血管。参照文献[7]，确定皮肤厚度为1.5 mm；由截面外轮廓和16个点的皮质厚度得到软组织的轮廓；参照文献[8]，确定骨骼尺寸。文中将骨骼截面假设为圆形，骨骼截面圆心与上臂截面外轮廓中心重合，最终得到上肢的截面模型，并将其拉伸2 cm高度，得到接触位置的3D模型，图4为上肢伸直放松状态下接触位置的3D模型。同样的步骤得到其余3种状态的3D模型。

图4 上肢伸直放松状态下接触位置3D模型Fig.4 3D model of the contact position

3.2 有限元模型建立

有限元法是将复杂的连续体划分为有限个简单的单元体，单元体之间仅采用节点相连，通过化整为零、再集零为整的手段对复杂问题进行分析[9]。

近年来，研究服装压的学者都将人体视为弹性体，并将人体分为皮肤层、软组织层和骨骼层，弹性模量分别为0.15，0.06和7 300 MPa[10]。温朝阳等[11]使用实时定量剪切波弹性成像超声诊断仪分析得出，紧张状态下的肱二头肌肌腹的杨氏模量为(123.658±31.392)kPa，松弛状态下的杨氏模量为(45.658±13.479)kPa。

假设模型各部分为各向同性均匀的线性弹性材料，人体由皮肤层、软组织层、骨骼肌层和骨骼层4个部分组成。表1列出了模型材料的属性及类型。将3D模型导入ANSYS Workbench17.0，设置皮肤的弹性模量为0.15 MPa，泊松比为0.46；软组织弹性模量为0.06 MPa，泊松比为0.49；骨骼的弹性模量为7 300 MPa，泊松比为0.30。由于骨骼肌在不同紧绷程度下的弹性模量是不同的，因此在骨骼肌的弹性模量范围内(45.658～123.658 kPa)均匀选取50，60，70，80，90，100，110，120 kPa 8个弹性模量数值用于动态分析，泊松比设为0.49。

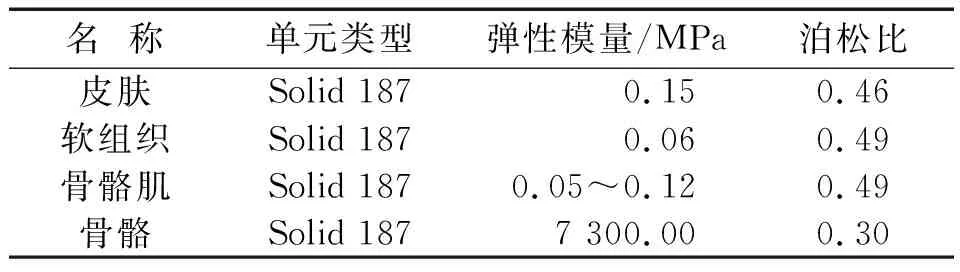
表1 材料属性和类型

各部分参数设定后，对模型进行四面体网格划分，网格尺寸为2 mm，划分结果得到46 576个单元和77 882个节点，图5为伸直放松状态下接触位置有限元模型的网格划分。

图5 接触位置3D模型网格划分 Fig.5 3D model meshing of the contact position

3.3 有限元模型的边界条件、加载和求解

接触位置的有限元模型中，由于骨骼最为坚硬，因此在模拟过程中，将骨骼受压后在X，Y，Z方向上的位移均为0设为模型的边界条件。本模型只考虑截面的位移情况，因此设皮肤层，软组织层，骨骼肌层的模型在Z方向的位移为0，在X，Y方向上自由移动。最后对皮肤表面加载法线方向的均等压力，压力为1 kPa，进行位移求解。可得到接触位置的位移分布图。

图6为接触位置在放松状态下的位移分布情况。图中不同颜色代表了不同位移的大小，其中位移分布图的左边颜色条从下至上表示位移逐渐增大，最上方的红色表示最大，最下方的蓝色表示最小，从图6可以看出接触位置的位移分布情况。同样的步骤可以得到其余3种状态下的位移分布。

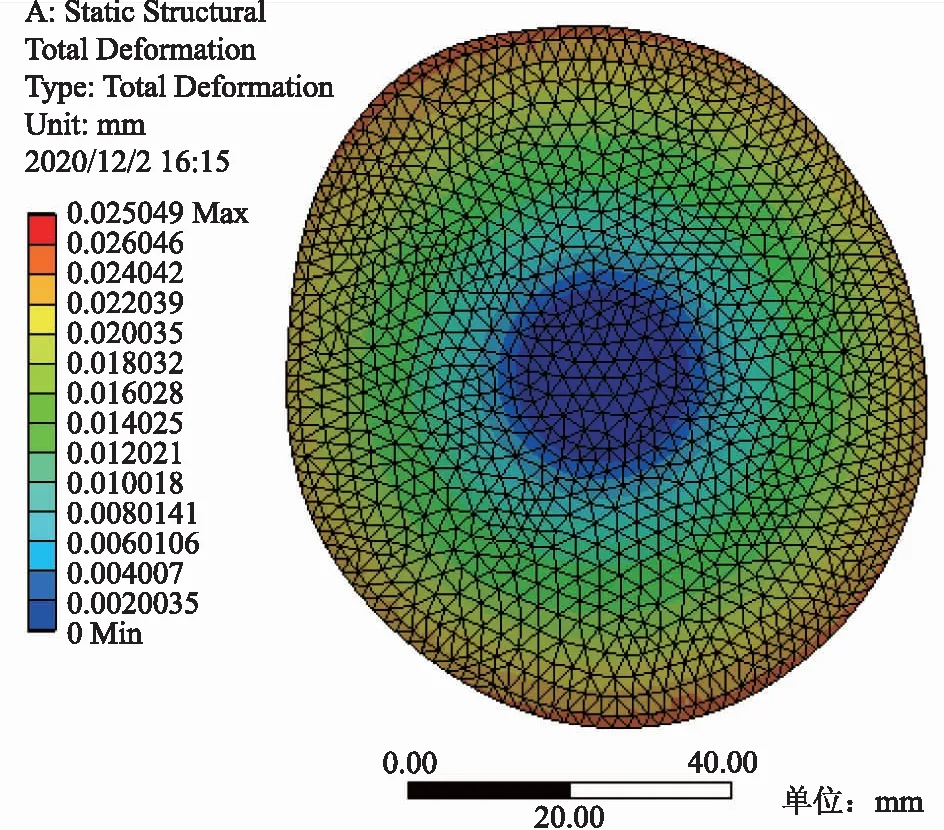
图6 伸直放松状态下接触位置的位移分布Fig.6 Displacement diagram under the extended and relaxed states

4 有限元仿真结果分析

4.1 4种状态的位移分布结果

通过ANSYS Workbench路径设置，可得到4种状态16个分析点在1 kPa均等压力下的位移情况，具体如图7所示。其中紧绷状态的骨骼肌弹性模量为0.12 MPa。

在同一种状态下，位移较大的区域在实际穿着服装时受到服装面压较大[12]。由图7可知，在伸直放松状态下，接触位置由于压力而产生位移较大的区域为135.0°～202.5°和292.5°～22.5°。16个分析点中最大位移为0.026 0 mm，在157.5°的位置。在弯曲放松状态下，位移变化较大的区域为67.5°～112.5°和292.5°～337.5°，16个分析点中最大位移为0.024 5 mm，在315°的位置；在伸直紧绷状态下，接触位置位移相对较大的区域为67.5°～135.0°。16个分析点中最大位移为0.014 6 mm，在90°的位置；在弯曲紧绷状态下，接触位置由于压力而产生位移较大的区域为22.5°～67.5°和180°～247.5°最大位移为0.015 6 mm，在202.5°的位置。通过对比4种状态的位移峰值可知，骨骼肌放松时，弯曲状态的位移峰值比伸直状态的大；骨骼肌紧绷时，弯曲状态的位移峰值同样比伸直状态的大。由此推得在同等压力和同种骨骼肌条件下，手臂弯曲状态时的最大压感要大于伸直状态时的最大压感。同时对比骨骼肌紧绷与放松状态下的位移可知，骨骼肌紧绷状态下的位移值远小于放松状态下的，因此在同等压力下，接触位置在不同状态下的压感差距较大。

图7 1 kPa压力下不同状态各分析点的位移情况Fig.7 Displacement of each analysis point in different states under 1 kPa pressure

4.2 位移的影响因素分析

由位移分布图可知，在相同压力下，不同状态的位移分布情况不同。针对这种现象，设定每个分析点的位移为S，分析点的曲率为ρ，骨骼中心的相对距离为d，皮质厚度为h，肌肉弹性模量为E，分析人体各结构因素对位移S的影响。表2列出了角度为0°的分析点在不同状态下各影响因素以及位移数据。

表2 角度为0°对应的分析点数据

运用SPSS软件对4种状态16个分析点的S,ρ，h，d，E进行相关性分析。位移与各影响因子的相关性见表3。由表3可知，在相关系数显著性概率水平为0.01的情况下，位移S与皮肤距骨骼的相对距离d以及皮肤表面的曲率ρ存在显著的相关性，与骨骼肌的弹性模量E存在显著的负相关。选取与位移Y相关性显著的因素进行多元线性回归分析，得到的线性回归方程为

表3 位移与各影响因子的相关性

Y=-0.934X1+0.256X2+0.037X3,

调整后的R2=0.931，拟合度较高。

通过分析相关系数可知，影响位移的主要因素为骨骼肌的弹性模量。当骨骼肌放松时，人体受压时容易发生位移和形变，可以适当缓冲着装时的压力；而当骨骼肌紧绷时，人体受压之后的形变能力降低，此时对服装压的缓冲能力下降，压感较强。在同种状态下，皮肤表面曲率越大的位置产生的位移越大，故在实际穿着服装时，受到服装的面压较大，进而压感较强。

由上述分析可知，在手臂弯曲紧绷状态下，上臂的形变能力降低，同时肱二头肌和肱三头肌隆起的区域(22.5°～67.5°,180°～247.5°)曲率较大，从而受到服装的面压较大。因此在优化手臂相关紧身纺织品时，应着重考虑手臂弯曲紧绷状态下的压力舒适性。

5 结语

文中运用逆行工程技术建立人体上臂伸直放松、弯曲放松、伸直紧绷、弯曲紧绷4种状态的有限元模型，将人体视为弹性体，建立人体皮肤层、软组织层、骨骼肌层、骨骼层4层人体有限元模型。考虑上臂不同状态的形态变化以及紧绷状态下骨骼肌的弹性模量变化，对不同状态的有限元模型模拟施加均等压力，得到不同状态接触位置的位移分布情况，并对每种状态下压感较大的区域进行了讨论。

运用SPSS对影响位移的上臂结构因素进行相关性分析，线性回归方程为Y=-0.934X1+0.256X2+0.037X3,调整后的R2为0.931，拟合度较高。结果表明，上臂骨骼肌的弹性模量、表面的曲率以及与骨骼的相对位置共同影响着着装后的位移。根据结论得出，施加均等压力下，4种状态中，上臂在弯曲紧绷的状态下，肱二头肌与肱三头肌所在的位置(22.5°～67.5°,180°～247.5°)服装压感相对较大。该结论可为上臂服装压力舒适性阈值研究中主客观评价分析点的选取以及相关紧身纺织品的优化设计提供理论参考。