异结构超混沌系统的多开关复合同步
2022-01-09张晓青
张晓青
(太原工业学院 理学系,太原 030008)
0 引言
组合同步于2008年被Runzi等人[1]率先提出,该同步类型包含两个驱动系统和一个响应系统,打破了混沌同步仅限于一个驱动、响应系统的局面.学者们先后提出了组合-组合[2-4]、双组合[5]等同步方法,它们都不是单驱动-单响应系统.需要特别注意的是,在通信保密应用中,有多个驱动响应系统的优势在于,所传输的信号可以被分成几个不同的部分,每个部分被加载到不同的驱动系统中,可以大大提高防御力.Ucar等人[6]在2008年提出的多开关同步方案是一个大胆而有趣的同步方案.在多开关同步方案中,由于驱动系统的不同状态变量同步于响应系统的不同状态变量(通常情况是驱动系统的第k个状态变量对应于响应系统的第k个状态变量),因此存在多种同步方案,进而增加抗攻击力.这类研究对于通信安全至关重要,而针对这一课题的研究却很少.Vincent等人[7]将多开关同步从单驱动/单响应系统扩展到双驱动/单响应系统.Shahzad[8]讨论了不同阶数整数阶的驱动和响应系统的多开关同步.Khan等人[9-10]研究了4个整数超混沌系统的多开关组合-组合同步,并在2017年实现了8个整数混沌系统的双组合-组合多开关同步状态.Zhang 等人[11]实现了3个复分数阶混沌系统和2个复整数阶混沌系统的复多开关复合-组合反同步问题.在实际情况中,分数阶系统较之整数阶系统更具有普遍性,且超混沌具有更大的不可预测性,因而对于分数阶混沌系统的同步研究具有更深远的价值.本文首先描述了复合同步(三个驱动系统与一个响应系统),然后在此基础上添加了多开关的设计,其次设计普遍适用于任何(相同或互异)的驱动、响应系统的控制机制,最后选取了三个常见的分数阶超混沌系统刘氏系统、陈氏系统、T系统作为驱动系统,以及一个分数阶超混沌响应系统Lorenz系统作为说明,从理论和数值仿真两个角度验证了所设计的输入机制的可行性和有效性.
1 相关理论
假设三个分数阶驱动系统为:
(1)
(2)
(3)
其中,0<α<1,xk=(xk1,xk2,……xkn)T∈Rn(k=1,2,3)为实状态向量,f1=(f11,f12,…,f1n)T,f2=(f21,f22,…,f2n)T,f3=(f31,f32,…,f3n)T为3个n维连续向量函数.记X11=diag(x11,x12,…,x1n),X21=diag(x21,x22,…,x2n),X31=diag(x31,x32,…,x3n).
三个分数阶混沌系统的复合信号为:
S=CX1(PX2+QX3)
(4)
其中C,P,Q∈Rn×n为实尺度对角矩阵,记C=diag(c1,c2,…,cn),P=diag(p1,p2,…,pn),Q=diag(q1,q,…,qn).
假设加入控制器的响应系统如下:
(5)
其中,y1=(y11,y12,…,y1n)T∈Rn为实状态向量,g1:Rn→Rn为n维实连续向量函数,u1为所要设计控制器,记Y1=diag(y11,y12,…,y1n)T.
矩阵形式下的误差系统为:
e=AY1-S
(6)
其中,A∈Rn×n为实尺度对角矩阵,A=diag(a1,a2,…,an).将式(4)代入(6),得
e=AY1-CX1(PX2+QX3)
(7)
其中e=diag(e1,e2,…,en).
定义1对于给定的驱动系统(1)-(3)和响应系统(5),如果存在非零常数对角矩阵A,C,P,Q∈Rn×n使得
(8)
则系统(1)-(3)和系统(5)实现了复合同步(CS).
注1e*=(e1,e2,…,en)T=e·(1,1,…,1)n×1T=[AY1-CX1(PX2+QX3)]·(1,1,…,1)n×1T
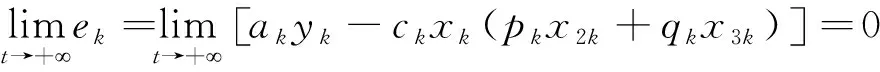
注3重新定义ek的分量如下:
eklms=aky1k-clx1l(pmx2m+qsx3s)
(9)
其中,k,l,m,s∈(1,2,…,n),下标(klms)代表y1的第k个分量,x1的第l个分量,x2的第m个分量,x3的第s个分量,对于定义1,则严格满足k=λ=m=s.
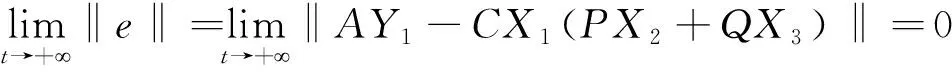
注4当X1=I时,多开关复合同步转化为了多开关组合同步.
注5当C=0时,多开关复合同步退化成了y1的控制问题.
定理1如果控制器设计为
(10)
此时,σk=aku1k,则驱动系统(1)-(3)与响应系统(5)实现了多开关复合同步.
证明:误差系统的导数为
(11)
(12)
令σk=aku1k,将(10)代入得
(13)
构造如下Lyapunov函数
(14)
对V求α阶导可得,
(15)
2 驱动系统和响应系统之间的多开关复合同步
2.1 系统描述
超混沌分数Liu系统[12]如下:
(16)
其中,x11,x12,x13,x14为Liu系统的状态变量,当系统的初始值选为(x11,x12,x13,x14)T=(-0.5,0.09,11,0.2)T时,系统变成混沌状态.
分数阶超混沌Chen系统[13]为:
建起了生态监测数据中心和各实施单位在内的分中心,建立了全省生态环境综合数据平台。生态监测信息已在有关规划编制、生态工程生态成效评估、三江源国家公园建设试点和自然资源资产负债表编制试点等工作中发挥着重要作用。
(17)
其中x21,x22,x23,x24为系统(2)的状态变量,当系统的初始值选为(x21,x22,x23,x24)T=(2,1,0.5,0.2)T时,系统(2)呈现混沌状态.
分数阶超混沌T系统[14]为:
(18)
其中x21,x22,x23,x24为系统(18)的状态变量,当系统的初始值为(x31,x32,x33,x34)T=(2,1,0.5,0.2)T时,系统(18)呈现混沌状态.
分数阶超混沌Lorenz系统[15]为:
(19)
其中y11,y12,y13,y14为系统(19)的状态变量,当系统的初始值为(y11,y12,y13,y14)T=(2,1,0.5,0.2)T时,系统(19)呈现混沌状态.
2.2 控制器的设计与数值仿真
任意选择一个开关,得到如下误差系统
(20)
定理2设计控制器如下
(21)
则多驱动系统(16)-(17)-(18)与单一响应系统(19)实现了多开关复合同步.
证明:误差系统(20)的导数为:
(22)
将系统(16)-(17)-(18)和(19)代入上式得:
(23)
将控制器(21)代入上式得:
(24)
Lyapunov函数选取为:
V=e*Te*/2
(25)
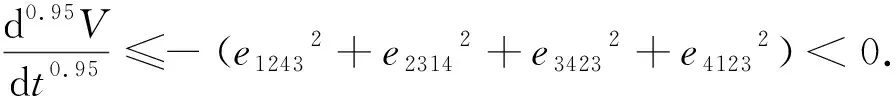
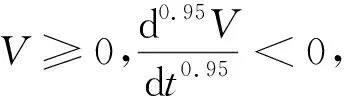
2.3 数值仿真
多驱动系统(16)-(17)-(18)与单一响应系统(19)的初始值随机选取为
(x11,x12,x13,x14)T=(-1.5,-1.5,4,0.2)T,(x21,x22,x23,x24)T=
(2,1,0.5,0.2)T,(x31,x32,x33,x34)T=(2,1,05,0.2)T,(y11,y12,y13,y14)T=(2,1,05,0.2)T.

图1 误差变化图
选取a1=3,a2=-4,a3=1,a4=2,c1=1,c2=-2,c3=3,c4=-1,p1=-2,p2=4,p3=6,p4=2,q1=-4,q2=3,q3=5,q4=2,则MSCS误差系统的初始值为
(e1243,e2314,e3423,e4123)T=(3,39.2,2.8,9.35)T.
图1描述了多开关复合同步(MSCS)误差随着时间的变化走势,可以明显看出误差很快就趋于了0,实现了多个驱动系统和单一响应系统在任意选定开关下的复合同步.
3 总结
本文首先刻画三个驱动系统和一个响应系统的多开关复合同步(MSCS)的概念,其次根据Lyapunov理论设计了普遍适用于任何混沌系统(三维或四维)的控制输入器.然后选择具体的驱动系统(分数阶超混沌刘氏、陈氏、T系统)、和响应系统(分数阶超混沌系统Lorenz系统),以及三个尺度矩阵设计了具体的控制输入器,并从理论上说明了其正确性,最后利用软件MATLAB进行仿真实验,验证了所设计控制输入器的合理性.
