Balanced Functional Maps for Three-Dimensional Non-Rigid Shape Registration

Xu-Peng Wang| Hang Lei | Yan Liu | Nan Sang

Abstract—Three-dimensional (3D) shape registration is a challenging problem,especially for shapes under nonrigid transformations.In this paper,a 3D non-rigid shape registration method is proposed,called balanced functional maps (BFM).The BFM algorithm generalizes the point-based correspondence to functions.By choosing the Laplace-Beltrami eigenfunctions as the function basis,the transformations between shapes can be represented by the functional map (FM) matrix.In addition,many constraints on shape registration,such as the feature descriptor,keypoint,and salient region correspondence,can be formulated linearly using the matrix.By bi-directionally searching for the nearest neighbors of points’ indicator functions in the function space,the point-based correspondence can be derived from FMs.We conducted several experiments on the Topology and Orchestration Specification for Cloud Applications (TOSCA) dataset and the Shape Completion and Animation of People (SCAPE)dataset.Experimental results show that the proposed BFM algorithm is effective and has superior performance than the state-of-the-art methods on both datasets.

Index Terms—Functional map (FM),Laplace-Beltrami operator,shape registration,three-dimensional (3D) non-rigid shape.

1.lntroduction

In recent years,with the fast development of three-dimensional (3D) scanning and computational devices,the acquisition and processing of depth data are becoming more and more efficient.There are a large amount of 3D shapes data.Compared with the traditional multimedia data,such as the image,audio,and video,depth data capture the geometric information of surfaces in a scene,and therefore show the pose of an object more accurately.Although it is insensitive to view changes or illumination,it is widely used in intelligent manufacturing,virtual reality,intelligent surveillance,robotics,remote sensing analysis,and so on[1]-[4].

The 3D shape registration is to compute the correspondence of shapes under different poses.It is a fundamental task in computer vision and computer graphics,and has been applied in 3D reconstruction,object recognition,and shape retrieval.A common transformation is isometric,where the geodesic distances between points remain stable.In the real world,there are a large amount of non-rigid transformations (approximately isometric),such as the articulation movement.Therefore,it is of great importance to compute the registration of 3D non-rigid shapes[5]-[10].

Most of the existing methods try to tackle the problem by first extracting some sparse matching point pairs and then extending to the whole shape.Since the matching points are sparse,it is necessary to incorporate additional constraints to ensure the accuracy of the shape registration,such as the geodesic distance between matching points[11],spectral features[12],and the standard domain based on matching feature points[13]or the global consistency of various geometric and topological feature combinations[14]-[16].However,since all the above algorithms are developed from point-based shape registration,it is a non-convex and non-linear problem,which is extremely hard to solve[17].

In this paper,we propose another 3D non-rigid shape registration method,called balanced functional maps (BFM).The algorithm generalizes the traditional point-based shape registration to functions.The Laplace-Beltrami eigenfunctions are adopted by the BFM algorithm as the function basis.Thus,non-rigid shape transformations can be represented as a functional map (FM) matrix.The point-based correspondence can be derived from FM through bi-directionally searching for the nearest neighbors of points’ indicator functions in the function space.The main contributions of this paper are as follows:

First,a representation of non-rigid shape transformation is proposed.Second,a shape registration algorithm is proposed based on the bi-directional nearest neighbor search.

2.FM

where Φaand Φbare the eigenfunctions.Thus,any functionf∈L2(M) can be represented as follows:

2.1.FM Definition

Given two 2D Riemannian manifolds M and N,there is a surjection between them,which is given as T ∶M →N .Thus,for any functionfdefined on M ,the corresponding functiongdefined on N can be derived according tog=f°T−1.Here,the operator ° denotes the composite function.

Therefore,FM between 3D shapes is defined as

Thus,FM can be formulated as follows:

2.2.Choice of Basis Function

Since FM is represented by a matrix,the standard linear algebra methods can be applied,and it is highly efficient to compute TF.The choice of the basis functions determines the compactness and robustness of the operations based on FM.Compactness means that the functions defined on 3D shapes can be represented with a small set of basis functions,while robustness means that the function space described by the basis functions remain stable under various shape transformations.

The Laplace-Beltrami operator,denoted as ΔM,is a generalization of the Laplace operator in the Euclidean space.It operates on the twice-differentiable functions defined on M,and describes the differences of function values between a point and its neighborhood.The Laplace-Beltrami operator is defined as the divergence of the function’s gradients,as follows:

The Laplace-Beltrami operator ΔMadmits the eigendecomposition ΔMΦi=λiΦiwith the eigenvalues 0=λ1≤λ2≤…≤λiand the corresponding eigenfunctions { Φi,i≥1}.The Laplace-Beltrami eigenfunctions are ordered with respect to the frequency and provide a standard orthogonal basis function forL2(M),which can be used to describe functions defined on M in multi-scales.In addition,the function space described by the first few eigenfunctions keeps stable under isometric transformations of a shape.

Therefore,with the non-rigid transformation T between them,the firstnLaplace-Beltrami eigenfunctions are adopted as the basis function for the function spacesL2(M) andL2(N).According to (1),the elementci,jof the matrix C is non-zero only if the eigenfunctionsandcorrespond to the same eigenvalues,i.e.,i=j.Thus,C is a sparse matrix.If the transformation T is approximately isometric,the matrix C is still close to sparse.

The illustration of shape registrations with the corresponding FM matrix is given inFig.1.There is an approximately isometric transformation between two cat models,which are from the Topology and Orchestration Specification for Cloud Applications (TOSCA) dataset[18].Three ways of shape registration are demonstrated,which are:(a) approximately isometric mapping,(b) left-to-right mapping,and (c) head-to-tail mapping.The point-based shape registration is shown with color correspondence.The first 20 Laplace-Beltrami eigenfunctions are used as the basis function,and FM is shown with the heat map of the map matrix C20×20.As shown inFigs.1(a) and (b),in approximately isometric transformation,the FM matrix is sparse,and close to a diagonal matrix.On the other hand,the matrix under the head-to-tail mapping does not have the property of sparsity.

Fig.1.Illustration of three shape registrations with FM matrix:(a) source,(b) ground truth,(c) left-to-right map,and (d)head-to-tail map.

2.3.FM Computation

Given two 2D Riemannian manifolds M and N ,letrepresent the firstnLaplace-Beltrami eigenfunctions defined on them,respectively.Denotef∈L2(M) andg∈L2(N) as a pair of corresponding functions,they can be represented by the coefficients vectors a=(a1,a2,…,an) and b=(b1,b2,…,bn),based on the Laplace-Beltrami eigenfunctions.

According to (7),FM betweenfandgcan be formulated as Ca=b.Therefore,the problem of shape registration can be solved by adding sufficient constraints,which can be regarded as functions defined on shapes,and are described by the FM matrix C linearly.

A.Feature Descriptor Correspondence

The correspondence between feature descriptors requires that the local features of points should be preserved under shape transformations as much as possible.Let f and g be thek-dimensional feature descriptors on M and N ,that is,f(x)=(f1(x),f2(x),…,fk(x)),g(x)=(g1(x),g2(x),…,gk(x)),and f(x),g(x)∈Rk.Each dimension of the feature descriptor provides a constraint for shape registration.

In this paper,the heat kernel signature (HKS)[19]withmdimensions and the wave kernel signature(WKS)[20]withndimensions are adopted,forming an (m+n)-dimensional feature descriptor,as follows:

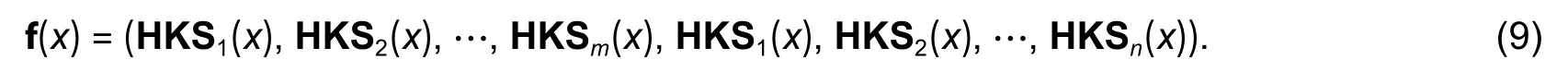
B.Keypoint Correspondence

Given correspondence between keypoints on 3D shapes,i.e.,T(PM)=PN,wherePM={∈M,1 ≤i≤n},PN={∈N,1 ≤i≤n},andnrepresents the number of keypoints.Letfandgbe the functions,which describe the distances between the keypoints and the rest of the points on the shape,i.e.,fi(x)=andfi(x),gi(x)∈R .The operator GD(⋅,⋅) calculates the geodesic distances between points.Thus,each distance function associated with a keypoint provides a constraint for shape registration.

In this paper,the persistence-based keypoint detection method[21]is adopted to select the firstksalient points,forming a distance function ofkdimensions,as follows:

where 1 ≤i≤k.

C.Salient Region Correspondence

Given correspondence between salient regions on 3D shapes,i.e.,T(RM)=RNT(PM)=PN,whereandnrepresent the number of salient regions on shapes.Letδi(x) be the indicator function of each salient region,andδi(x) is defined as follows:

Thus,each indicator function of a salient region provides a constraint for shape registration.

In this paper,the scale space clustering evolution algorithm[22]is used to extractksalient regions onM and N ,producing an indicator function ofkdimensions,as follows:

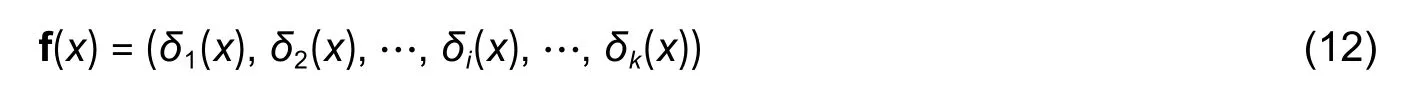
where 1 ≤i≤k.

3.Shape Registration Based on Balanced FM

Given two 3D shapes M and N ,represent them by 3D triangle meshesMandN,respectively.There are non-rigid transformations between M and N,which can be approximated by an isometric transformation T ∶M →N .Suppose FM TFis given,and its mapping matrix is C.

The Laplace-Beltrami eigenfunctions ΦM,ΦN∈Rn×kcan be looked as functions defined on M and N ,the number of which isn.It satisfiesThe point-based correspondence can be described by a permutation matrix P ∈(0,1)n×n.Thus,the FM matrix can be formulated by ΦM,ΦN,and P,as follows:

where C =(ci,j)∈Rk×kand its rank isk.

Deriving shape registration from FM TFmeans calculating P for given ΦM,ΦN,and C,that is,

satisfying PTI=I and P I=I.HereD(⋅,⋅) represents a measureof distance.

Denote the indicator function of the pointxon M ,as follows:

The indicator function can be represented as a linear combination of the Laplace-Beltrami eigenfunctions,as follows:

According to (7),the corresponding indicator function of the pointx′on N can be comput ed as follows:

In this way,the corresponding indicator functions of all points can be derived.Equation (14) is transformed as a linear assignment problem,that is,

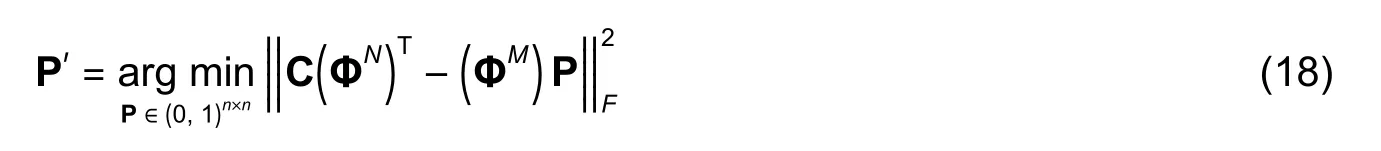
satisfying PTI=I and P I=I.Here,‖ ⋅‖Frepresentsthe Frobenius norm.

To solve the problem of one-to-many point mappings[17],[23],an additional constraint is introduced,producing the balanced FM:

satisfying PTI=I,P I=I,QTI=I,and Q I=I.

To further reduce the complexity,the linear assignment problem (as shown in (19)) is solved by using the nearest neighbor search method.In our implementation,we compute an approximate solution by alternating minimization on P and Q.The final matrix (P or Q) is the derived permutation matrix,which is the computed point-based representation of shape registration.

4.Experiment

In this section,a series of experiments are conducted to examine the effectiveness of the proposed BFM algorithm.First,the experiments were carried out on the TOSCA dataset[18]to evaluate the performance of the BFM algorithm with different Laplace-Beltrami operator discretization methods or different numbers of eigenfunctions.Then,the performance of the BFM algorithm is tested and compared with the state-of-the-art methods on two datasets,i.e.,the TOSCA dataset and the Shape Completion and Animation of People(SCAPE) dataset[24].

4.1.Evaluation Methods

According to [25],the average geodesic error (AVE) and the matching rate (MR) are adopted to evaluate the performance of shape registration methods.

Given two 3D shapesM1andM2,there are the ground truthftrue∶M1→M2and a computed shape registration resultf∶M1→M2.For a pointp∈M1,its matching error is defined as the geodesic distance(f(p),ftrue(p)) between its computed matching pointf(p) and the ground truthftrue(p).

Thus,AVE is defined as

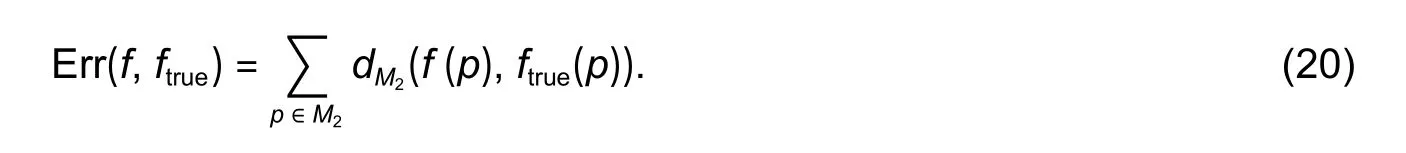
To eliminate the effect of shape scaling,AVE is normalized,as follows:

where A rea(⋅) calculates the surface area ofM2.

Given a geodesic distance errorr,for a pointp∈M1,if the geodesic distancedM2(f(p),ftrue(p)) between its computed matching pointf(p) and the ground truthftrue(p) is less thanr,the pointpis said to be correctly matched.MRM(r) is defined as the percentage of correctly matched points on a shape according tor.

4.2.Experiments on TOSCA Dataset

The TOSCA dataset consists of nine models,i.e.,Cat,Centaur,David,Dog,Gorilla,Horse,Michael,Victoria,and Wolf.Each model contains a symmetric null shape and its transformed shapes with approximately isometric transformations,producing 80 models in total.The point-based correspondence between the transformed shapes and their corresponding null shape is known as prior information,called the ground truth.The number of points on each shape ranges from 5000 to 50000.

In this section,we first evaluate the performance of the BFM algorithm on the Cat model,with different Laplace-Beltrami operator discretization methods or different numbers of eigenfunctionsnE.The functional mapping matrix is computed using the ground truth,and the proposed BFM method is applied to compute the point-wise shape registration.AVE is adopted to evaluate its performance.Two widely used Laplace-Beltrami operator discretization methods were tested,i.e.,the cotangent weight scheme (CWS) and area normalized cotangent weight scheme (ANCWS).The number of eigenfunctions ranges from 1 to 300.The experimental result is shown inFig.2.

We can learn fromFig.2that the unnormalized discretization method is able to represent FM more compactly.It means that a smaller matching error is achieved with the same number of eigenfunctions.Because the surface area may change during shape transformations,and the ANCWS method is more sensitive.In addition,while the number of eigenvaluesnEincreases from 1 to 50,AVE is reduced significantly.This is because that the additional eigenfunctions improve the accuracy to describe FM.When only 30 to 40 eigenfunctions are used,the BFM algorithm achieves a small error,and is more capable of encoding shape registration.However,as the number of eigenfunctions increasing,the size of the FM matrix is enlarged.At the same time,the computational and storage cost is increased.

Fig.2.Performance of the BFM algorithm on the Cat model.

We tested the BFM algorithm on the TOSCA dataset,and compared with the state-of-the-art methods,i.e.,FM and blended intrinsic maps (BIM).The experimental result is shown inFig.3.

We can learn fromFig.3that the proposed BFM algorithm improves the best performance on the TOSCA dataset.When the geodesic distance error is 0,the BFM method is able to successfully find almost 40% matching points,while only 20% can be achieved by the FM algorithm.When the error is at around 0.10,the proposed BFM can produce shape registration with almost full accuracy.In contrast,the FM method gets a full score at 0.15.

Fig.3.Performance of the BFM,FM,and BIM algorithms on the TOSCA dataset.

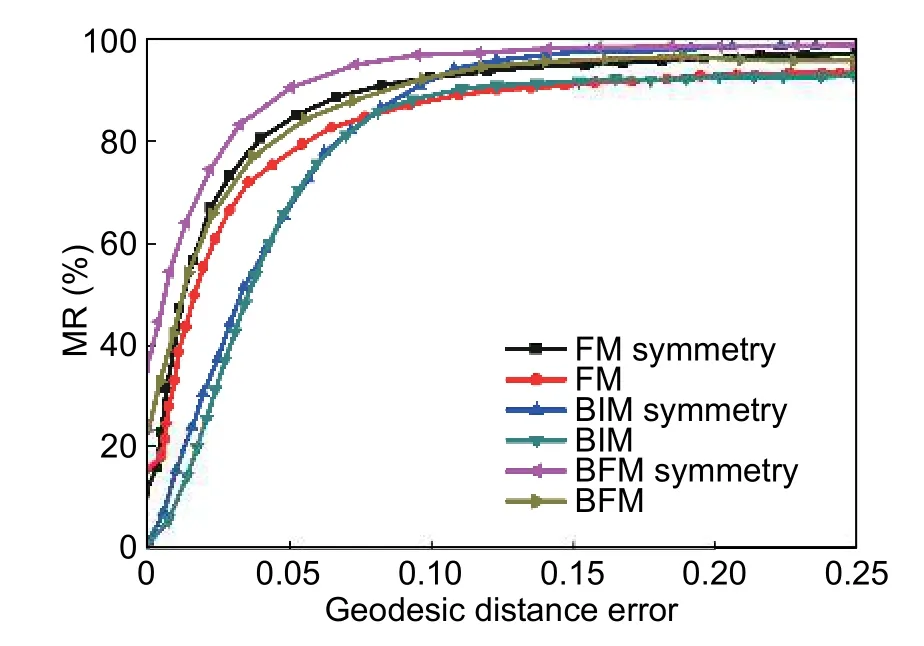
Fig.4.Performance of the BFM,FM,and BIM algorithms on the SCAPE dataset.

4.3.Experiments on SCAPE Dataset

In this section,the proposed BFM algorithm is tested on the SCAPE dataset,and also compared with FM and BIM methods.The MR measure is adopted to evaluate the performance of shape registration.The experimental result is shown inFig.4.

We can learn fromFig.4that the proposed BFM algorithm improves the performance of the current state-of-the-art on the SCAPE dataset.Particularly,when the geodesic distance error is set to be 0,the BFM algorithm is able to find almost 40% matching points,in comparison with 10% achieved by the FM method and 5% by the BIM method.

5.Conclusions

In this paper,a 3D shape registration method is developed,which can deal with shapes under non-rigid transformations.The proposed BFM algorithm generalizes the traditional point-based correspondence to functions.By choosing the Laplace-Beltrami eigenfunctions as the function basis,non-rigid transformations of 3D shapes can be represented as an FM matrix.The point-based correspondence can be derived from FM using the bi-directional nearest-neighbor search to obtain the points’ indicator functions in the function space.Experimental results show that the proposed algorithm is effective and improves the current state-of-the-art performance.

Acknowledgment

The authors would like to acknowledge Prof.Michael Bronstein for providing the TOSCA dataset.The authors also acknowledge Prof.Daphne Koller for providing the SCAPE dataset.

Disclosures

The authors declare no conflicts of interest.