Effects of Material and Dimension on TCF,Frequency,and Q of Radial Contour Mode AlN-on-Si MEMS Resonators
2022-01-08ThiDepHa
Thi Dep Ha
Abstract—This paper investigates the effects of material and dimension parameters on the frequency splitting,frequency drift,and quality factor (Q) of aluminium nitride (AlN)-on-n-doped/pure silicon (Si) microelectromechanical systems (MEMS) disk resonators through analysis and simulation.These parameters include the crystallographic orientation,dopant,substrate thickness,and temperature.The resonators operate in the elliptical,higher order,and flexural modes.The simulation results show that i) the turnover points of the resonators exist at 55 °C,-50 °C,40 °C,and -10 °C for n-doped silicon with the doping concentration of 2×1019 cm-3 and the Si thickness of 3.5 μm,and these points are shifted with the substrate thickness and mode variations;ii) compared with pure Si,the modal-frequency splitting for n-doped Si is higher and increases from 5% to 10% for all studied modes;iii) Q of the resonators depends on the temperature and dopant.Therefore,the turnover,modal-frequency splitting,and Q of the resonators depend on the thickness and material of the substrate and the temperature.This work offers an analysis and design platform for high-performance MEMS gyroscopes as well as oscillators in terms of the temperature compensation by n-doped Si.
Index Terms—Anisotropic,contour mode,doping,gyroscope,microelectromechanical systems (MEMS) resonator,piezoelectric,temperature coefficient of frequency (TCF),temperature compensation,thin-film piezoelectric-onsubstrate (TPoS).
1.lntroduction
Microelectromechanical systems (MEMS)[1]resonators have been exploited in many applications (e.g.,oscillators[2],[3],filters[1],[4],[5],radar systems,and communications systems or gyroscopes[6]-[10]) due to a small form factor and integration with the complementary metal oxide semiconductor (CMOS)[11].Such contour mode based MEMS disk resonators have been reported[7]-[12].
Some of the critical parameters which can affect the resonator performance are the frequency splitting[8]-[10],[12]-[14],frequency drift[15],[16],and quality factor (Q)[11],[17].For instance,an increasedQand a matched modal frequency can improve the gyroscope’s sensitivity and reduce the phase noise[10],[18],[19].The mode matching is to match the resonant frequency between the drive and sense modes and thus to eliminate the frequency splitting[9],[10],[13].The modal frequency of a resonator is the frequency obtained in eigenfrequency analysis when the resonator does not been supplied by external loads.The frequency splitting is the frequency difference between the drive-mode and sense-mode frequencies.Also,the discrepancy between the frequency temperature characteristics affects the resonator’s temperature stability performance[20]-[22].
One of sources causing the frequency splitting is the anisotropic properties of structure composite materials[8],[9],[23]-[26].To reduce the frequency splitting,most elliptical mode gyroscopes are fabricated in more isotropic materials,such as polysilicon[17],[27]and (111) Si[28].
The temperature dependence on elastic constants[29]-[34]of the composite structure materials is the cause of the frequency drift in MEMS resonators[32],[35],[36].Hence,the resonant frequency stability over temperature is one of important parameters to evaluate the performance of resonators.Besides the doping effects on the frequency drift,it is necessary to consider them on the frequency splitting.In addition,many studies only focused on the impacts of Si anisotropic properties on the frequency splitting[8]-[10],[13].However,to the best of the author’s knowledge,the effects of the temperature,dopant,and substrate thickness on the frequency splitting and frequency drift of piezoelectric MEMS disk resonators with the elliptical,higher order,and flexural modes have been reported up to now yet.
The higher theQ,the more the sensitivity and the lower the phase noise[11],[17].Except that the impacts of the geometrical structure of the support tether onQhave been investigated widely[37]-[41],this work focuses on the influences of dopant and temperature.Hence,we only concentrate their influences onQof the thermoelastic damping (TED) (QTED)[42]-[46]and support loss (i.e.,anchor loss) (Qanchor)[37],[38].
The aim of this paper is to present the effects of the material and dimension on the frequency andQof thin-film piezoelectric AlN-on-n-doped/pure Si disk resonators for gyroscopes.These resonators operate in the contour,higher order,and flexural modes.The material properties and dimension include the crystallographic orientation,dopant,temperature,and substrate thickness.The frequency characteristics include the model frequency,frequency drift,and frequency splitting.
The main contribution of this paper is summarized as follows:
1) The analysis,simulation,and evaluation of the effects of material (e.g.,temperature,dopant,and crystallographic orientation) on the modal frequency,frequency drift,frequency splitting,andQare presented.
2) First,we evaluate the change of the modal frequency along with these parameters.Second,the dependence of the frequency drift on the temperature and substrate thickness for the n-doped/pure Si based resonators is also simulated to determine the turnover point (i.e.,temperature stability point) of the resonators.Qof the resonators is affected by these parameters.
3) The analysis,simulation,and evaluation of the effects of the dimension in terms of the substrate thickness on the frequency drift and frequency splitting are studied.
4) The comparison of frequency characteristics andQbetween pure and n-doped Si based resonators in each mode is also studied.
The design is simulated and computed by using finite element analysis in COMSOL Multiphysics and MATLAB.
2.Materials and Method
2.1.Materials
2.1.1.Dependence of Si Elastic Constants on Temperature and Doping Concentration
To evaluate the temperature-induced frequency drift,the linear temperature coefficient of frequency (TCF)is expressed in a general form as follows[33]:

whereTis the temperature;fis the resonant frequency of the thin-film piezoelectric-on-substrate (TPoS)resonators and is expressed in a general form as=whereMis a coefficient depending on the dimension and resonant mode of the resonators,Eeffis the effective Young’s modulus,andρeffis the effective mass density of the structure composite materials in the TPoS resonators.
For the TPoS disk resonator,this resonant frequency is discussed in detail in the following subsection 2.2.
To predict TCF of the MEMS resonators with n-doped Si,a method combining Keyes’ theory[47]based quantitative calculation of the influence of free electron on elasticity and the finite element simulation based numerical analysis is applied.This Keyes’ theory shows that the elastic properties of n-doped Si depend upon the electron concentration.In the case of n-doped Si,the elastic constant variation at absolute temperatureTdue to the dopant is determined by[48],[49]

whereNis the electron concentration,Efis the Fermi energy,Ξis the shear deformation potential constant,andX(T) is the function defined by

whereηis given byEfoverkT;FandF′are the Fermi integral and its derivatives,which were defined in [50]to [52].The elastic constants of Si at absolute temperatureTare determined by[32],[48]
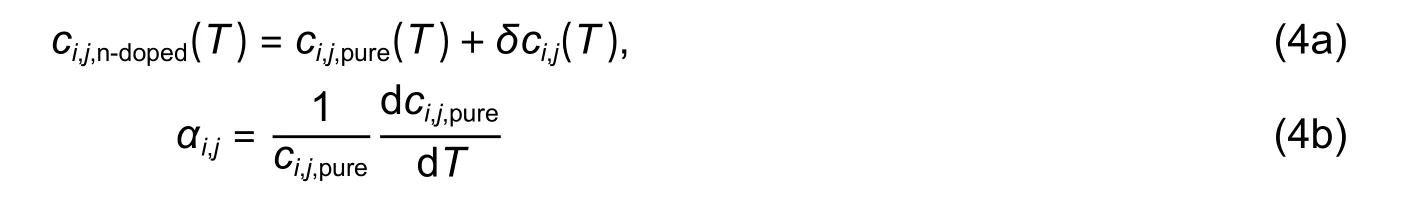
whereαi,jis the elasticity temperature coefficient (i.e.,thermal coefficient);(i,j)={(11),(12),(44)}.
In our work,the temperature dependent elastic constants for pure and n-doped Si are calculated based on the measured data from [34] and[49] and combined with (2) to(4).The values of Si elastic constants at 25 °C are listed inTable 1.The theoretical prediction also agrees well with the experimental results reported in [34] for a similar doping concentration level.

Table 1:Material properties of AlN[26] and Si[34]
Additionally,the temperature dependence of AlN Young’s modulus and Poisson’s ratio is calculated from the measured data and formulas in [29] and [30].
Fig.1illustrates the Si elastic constants versus temperature using Keyes’ theory for the doping concentrationNof 2×1019cm-3.This calculated result agrees with the measured data in [34] and [49].

Fig.1.Calculated elastic constants versus temperature for pure and n-doped Si:(a) c11,(b) c12,and (c) c44.
2.1.2.Dependence of Elastic Constants of Si and AlN on Crystallographic Orientation
Si is a material belonging to the cubic system[23],[53]while AlN belongs to the hexagonal system[25],[53],[54].Both Si and AlN are the anisotropic crystalline materials.Their material properties depend on the orientation relating to the crystal lattice.It means that the exact value of Young’s modulus (E) for analyzing two different designs may differ from each other[23].For instance,the value ofEin the planar direction varies between 130 GPa to 188 GPa for the <100>and <111>directions,respectively[23].
The material matrices of Si and AlN are given in Appendix A.
The dependence of the stiffness and compliance of Si and AlN on the crystallographic orientation is calculated and predicted using the bond matrix based transformation law and Euler angle[55]as follows:
For a converted stiffness form,its expression is given by
or in a converted compliance form as

where s and c are the stiffness and compliance matrices,respectively;M and N are the bond transformation matrices given in Appendix B.
Young’s moduli and Poisson’s ratios of AlN and Si in any crystallographic orientations can be determined by[24],[56]

Fig.2shows the crystallographic orientation dependence on Young’s moduli,elastic constants,and Poisson’s ratios of Si and AlN in the (100) plane.Figs.2 (a)and(b)illustrate the pure and n-doped Si Young’s moduli and elastic constants versus the crystallographic orientation.The AlN Young’s modulus is shown inFig.2 (c).The Poisson’s ratios of Si and AlN are plotted inFig.2 (d).
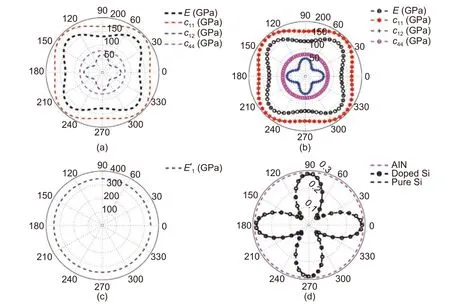
Fig.2.Polar plots.Calculated Young’s moduli and elastic constants of (a) pure Si and (b) n-doped Si,(c) calculated Young’s modulus of AlN,and (d) Poisson’s ratios of AlN,pure Si,and n-doped Si.
2.2.Method
2.2.1.Model of Resonators
Fig.3illustrates the schematic view of the elliptical mode TPoS resonator based gyroscope.The resonator operation bases on the direct and reverse piezoelectric effects occurring in the thin-film piezoelectric plate.An applied electric field across the film sandwiched between two metallic electrode layers generates the strain.This strain causes the deformation of the whole structure through the reverse piezoelectric effect.This vibration then induces charges on the metallic electrode surfaces through the direct piezoelectric effect.The disk-like gyroscope vibrates in the in-plane modes,which involves both radial and circumferential displacements in the disk and utilizes a degenerate vibration mode pair as the drive mode and the sense mode.

Fig.3.Schematic view of (a) resonator in the case of top electrodes for the elliptical mode and (b) symmetrical part of the center support tether,PML,and resonator body.
The displacement components of the disk resonator can be expressed as[8],[10]

wherekmandhmare the dimensionless frequency parameters for themth mode,Ris the radius of the disk,AmandBmare the constants,andJmis the Bessel function of the first kind.The resonance frequency of the resonator is given as[8]

whereνeffis the effective Poisson’s ratio of the structure composite materials.
Eeff,νeff,andρeffare calculated from [57]

wherePeqis the effective Young’s modulus,Poisson’s ratio,or mass density of the structure composite materials;Pjis the Young’s modulus,Poisson’s ratio,or mass density of the materialj;tjis the thickness of the materialj;jis the metallic electrode,piezoelectric,or substrate materials,respectively.
Here it can be seen that the metallic top and bottom electrodes are made of isotropic materials while the piezoelectric and Si substrate materials are anisotropic.The mass density is independent on the crystallographic orientation.Hence,the modal resonant frequency of the disk resonators depends onEandνof piezoelectric and Si materials (i.e.,depend on elastic constants).Due to the elastic constant difference in arbitrary crystallographic orientations,Eandνmaybe have different values for these corresponding orientations.
The designed disk has a 50-μm radius.It consists of a 0.5-μm AlN piezoelectric thin film,a 3.5-μm Si substrate,and 0.1-μm molybden (Mo) electrodes,as shown inFig.3 (a).The center support tether has the lengthLTofλ/16 (λis the wavelength) and the tether radius of 5 μm.The radius of the spherical tetherRTisλ/4.Fig.3 (b)illustrates the tether configuration,resonant body,and perfectly match layer (PML)[5],[37],[38].
2.2.2.Modeling
The simulation in our work is performed via COMSOL and post processing results are then processed and computed by MATLAB.The simulation scenarios referring to the temperature dependent parameters are carried out by combining the parametric sweep.Qof the resonators depends on several loss sources[37],[38].However,as discussed in Section 1,we only focus onQTEDandQanchorin this work.Other losses are assumed not to affectQ.Hence,Qis calculated by using

To predictQanchorof the resonators,PML in COMSOL is used to model the anchor loss.PML is a mimic domain that absorbs all energy from the tether to the substrate and prevents the waves back to the device,and thus allows losing energy to the surroundings[58].The resonators are anchored at the center of the disk.Qanchorcan be obtained by[38]

whereωis the eigenfrequency of the desired mode of the resonators solved via FE simulation in COMSOL.Also,the thermoelasticity (te) module in COMSOL is utilized to model TED.QTEDis also obtained by applying(12).The material parameters which are used in simulation are also listed inTable 1.
3.Results and Discussion
3.1.Model Mode Shape
The eigenmode shapes of degenerate vibration mode pairs of the elliptical and its higher order modes as well as the flexural mode occurring in the resonator are illustrated inFig.4.Figs.4 (a)and(b)show the elliptical degenerate mode pair with the oblique angle of 45°.Figs.4 (c)and(d)demonstrate the third degenerate mode pair with the oblique angle of 30°.This angle is 15° for the fourth mode,which is illustrated inFigs.4 (e)and(f).For the flexural mode,the angle is 45°,as shown inFigs.4 (g)and(h).

Fig.4.Simulated eigenmode shapes of the degenerate vibration mode pairs of (a) and (b) elliptical mode,(c) and (d) third mode,(e) and (f) fourth mode,and (g) and (h) flexural mode.
3.2.Model-Frequency Drift versus Temperature,Dopant,and Substrate Thickness
Fig.5illustrates the frequency-temperature characteristics of the elliptical,third,fourth,and flexural modes corresponding with pure and n-doped Si.For n-doped Si,the simulated frequency drift versus temperature results in a resemble parabolic trend with the turnover point[32].The turnover points occur at 55 °C,-50 °C,40 °C,and -10 °C for the elliptical,third,fourth,and flexural modes,respectively,which are indicated by the circle-marked black,triangle-marked blue,diamond-marked yellow,and hexagram-marked cyan lines,respectively.The turnover points for the elliptical mode and its fourth mode are close to the room temperature point,while the ones for the flexural and third modes are towards a lower temperature range (i.e.,to the negative direction of the axis).In particular,the turnover point of the third mode tends to out of the temperature range.
On the contrary,the TCF constants are approximate -22.34 ppm/°C,22.21 ppm/°C,22.45 ppm/°C,and 23.43 ppm/°C for pure Si (no turnover point existence).These TCF constants insignificantly change among the different modes.Specifically,these facts indicate that the elastic constants have impacts on the change of the frequency of the distinct modes.
The substrate thickness dependence of the temperature induced frequency drift is illustrated inFig.6.

Fig.5.Dependence of simulated frequency drift on n-doped and pure Si for elliptical,third,fourth,and flexural modes.

Fig.6.Dependence of the simulated frequency drift on the n-doped Si thickness of the resonator with (a) elliptical mode,(b) third mode,(c) fourth mode,and (d) flexural mode.
Fig.6shows that the turnover point is affected by the substrate thickness.However,these points are towards the positively higher temperature range when the substrate thickness becomes thicker (manifested by the offset center in the figure).Fig.6 (a)illustrates the turnover points with the substrate thickness varying from 3 μm to 6 μm for the elliptical mode.These values are 50 °C,55 °C,60 °C,70 °C,and 75 °C,corresponding to the substrate thickness of 3.0 μm,3.5 μm,4.0 μm,5.0 μm,and 6.0 μm,respectively.The thicker the substrate,the higher the value of the turnover point.For the third mode,the turnover points concentrate around 45 °C and may be pushed out of the temperature range when the Si thickness becomes thinner,as shown inFig.6 (b).The turnover points are approximate in the range from 20 °C to 60 °C for the fourth mode and are illustrated inFig.6 (c).These points shift to lower values for the flexural mode,about -15 °C to -5 °C,as plotted inFig.6 (d).These simulated results can be explained based on the graph shown inFig.1and the formulas in [59].It means that the dopant causes the variation of the elastic constants of Si.As a result,the resonant frequency of the resonators depends on these elastic constants.
3.3.Modal Frequency and Frequency Splitting versus Crystallographic Orientation and Dopant
The crystallographic orientation dependence of the modal frequency and frequency splitting is illustrated inFig.7.These results are simulated using the parameters of Si and AlN at 25 °C.As shown inFig.7 (a),the modal frequency of the resonators with different modes increases when the rotation angle is higher.This is due to the increase of Si Young’s modulus,as calculated in subsection 2.1 and plotted inFig.2.The frequency splitting for the elliptical mode achieves the highest as compared with the other simulated modes,about 5.63 kHz and 5.91 kHz corresponding to pure and n-doped Si and 0° rotated-orientation.This frequency splitting for the third,fourth,and flexural modes in pure Si is 0.342 kHz,2.080 kHz,and 1.100 kHz,respectively.Similarly,these values are 0.372 kHz,2.290 kHz,and 1.020 kHz for n-doped Si.The detailed values are shown inTable 2,where*indicates kHz;a and b represent pure Si and n-doped Si,respectively;1 to 4 denote the elliptical,third,fourth,and flexural modes,respectively.The graph for the frequency splitting is illustrated inFig.7 (b).Compared with pure Si,the frequency splitting for n-doped Si increases up to 5.0%,8.8%,10.1%,and 7.3% for the elliptical,third,fourth,and flexural modes,respectively.

Table 2:Effects of the crystallographic orientation and dopant on the frequency splitting of the resonator for the elliptical,third,fourth,and flexural modes

Fig.7.Dependence of simulated (a) modal frequency and (b) frequency splitting on pure/n-doped oriented Si and AlN and vibration modes.
In summary,in all simulated cases,the frequency splitting for n-doped Si is always higher than the one for pure Si.These can be explained that the difference among the values of the frequency splitting for pure and n-doped Si is due to the different dependence of the elastic constantsc11andc12on the temperature,as shown inFigs.1 (a)and(b).
3.4.Q versus Dopant and Temperature
Fig.8illustratesQof the resonators for n-doped (the marked blue lines) and pure (the marked red lines)Si.Qis computed using (11).Fig.8 (a)showsQfor the elliptical mode in both cases of n-doped and pure Si.The results indicate that the higher the temperature,the lower theQ.For the third mode,whileQis reduced for pure Si,it is increased for n-doped Si when the temperature is higher,as shown inFig.8 (b).TheQvalues of the fourth and flexural modes increase more and more when the temperature is towards to positively higher values,as shown inFigs.8 (c)and(d).Qwith n-doped Si is only higher than the one with pure Si corresponding with the elliptical mode.The detailed values are listed inTable 3for the temperature of 25 °C.It can be concluded thatQis affected by bothQanchorandQTED.Obviously,the dopant and temperature are the causes of the changes in these parameters.

Table 3:Simulated QTED and Qanchor of resonators with different modes for n-doped and pure Si (@25 °C)
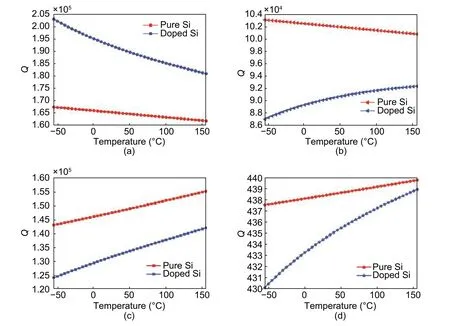
Fig.8.Dependence of Q on the temperature for pure and n-doped Si with (a) elliptical mode,(b) third mode,(c) fourth mode,and (d) flexural mode.
Fig.9plotsQanchorof the resonator with the flexural mode versus the mesh element number.
The following conclusions can be concluded:
1) For n-doped Si,the existence of turnover points tends to shift to the lower temperature when the mode order is higher with the same doping concentration.
2) For pure Si,the TCF constants are approximate up to 22 ppm/°C for all simulated modes.
3) The higher the value of the turnover point,the thicker the substrate.
4) The resonant frequency is a function of temperature and dopant.
5)Qof the resonator depends on the dopant,temperature,and vibration mode.

Fig.9.Qanchor versus the mesh element number for the flexural mode.
4.Conclusion
In this paper,we presented the simulation of the impacts of the substrate thickness,dopant,and temperature on the modal frequency,frequency drift,andQof the AlN-on-Si resonators with different modes for gyroscopes as well as oscillators.The vibration modes studied in our work included the elliptical and its higher order modes and the flexural mode.Furthermore,the comparison of performance parameters was also carried out between n-doped and pure Si in our work.The simulated results show that the performance of the resonators changes as the material properties and thickness of the resonators vary.
Appendix
Appendix A
The standard Si and AlN stiffness (i.e.,elastic) matrices are given as follows[53]:
1) For the cubic system,

2) For the hexagonal system,

Appendix B
The bond transformation matrices M and N are denoted as

whereai,j(i,j=x,y,z) is the element of the coordinate transformation matrix a that is given by

whereθis the rotation angle.
Acknowledgment
The authors wish to thank the anonymous reviewers for his/her efforts in spending time to process our paper.
Disclosures
The authors declare no conflicts of interest.
杂志排行
Journal of Electronic Science and Technology的其它文章
- lmpact of Fiber Dispersion on Performance of Entanglement-Based Dispersive Optics Quantum Key Distribution
- Effect of lmpeller Solidity on the Generating Performance for Solar Power Generation
- Large-Capacity and High-Speed lnstruction Cache Based on Divide-by-2 Memory Banks
- Effect of Wall Thicknesses on Broadband Design of Ka-Band TE21-Mode Coupler
- Device-Free Through-the-Wall Activity Recognition Using Bi-Directional Long Short-Term Memory and WiFi Channel State lnformation
- Balanced Functional Maps for Three-Dimensional Non-Rigid Shape Registration
