基于Elman 神经网络模型的短期电力负荷预测模型

包满

（四川大学华西医院，四川成都 610041）

电力负荷预测是电力分配调度的基础，也是电力发展规划的依据，提高电力负荷预测的准确率，对增加电力系统效益，维护电力系统稳定有着至关重要的意义[1]。随着计算机技术和大数据理论的发展，智能化方法不断兴起，大数据分析理论和智能化技术在电力负荷预测中的应用研究越来越多，智能化负荷预测系统逐渐成为电网管理系统中专门的子系统[2]。人工神经网络算法凭借强大的自学习能力和非线性映射能力，在电力负荷预测模型中取得了良好的预测效果。但传统的神经网络模型存在一些不足之处，如训练周期长、容易陷入局部最优值等[3]。此次研究以Elman 神经网络模型进行短期电力负荷预测，并对其进行算法优化及仿真实验，通过优化后的算法可以提高负荷预测的精度。

1 人工神经网络算法的关键技术

1.1 人工神经网络算法

人工神经网络通过对负荷数据的内在变化规律进行分析，从而对输入变量和负荷建立数学函数表达，其特点在于高度的非线性、自适应和自学习性、并行分布处理以及容错性。由于神经网络的基本结构是神经元之间的分布式连线，因此在数据量较大的情况下，可以进行信息的并行分布处理，这一结构保证了算法处理效率[4]。作为神经网络的基本组成单元，神经元的结构如图1 所示。

由于在平面阻尼型欠驱动夹持器连杆间添加了弹簧力，使得该机构满足最小阻尼定律[18]，即沿最小阻尼方向运动时，尽管其自由度数目大于驱动数目，也不会呈现运动状态不确定的现象。图1为典型的二自由度平面阻尼型欠驱动夹持器，其中：β为EA与水平方向的夹角，γ为杆3和杆5之间的夹角；v为点E到夹持器对称轴的距离，G为夹持器最大开口范围。夹持器左右对称，以右侧结构为例，弱弹簧安装于驱动杆1、推动杆2之间，可在运动过程中对铰链B添加阻尼。由于弹簧刚度很小，在建立夹持力模型时弱弹簧力可以忽略不计。

老四翻转一下手里的枪，把枪管顶在皮特的脑门上，将子弹上膛。皮特张着嘴僵在那里，一动不动，哈欠打到一半。

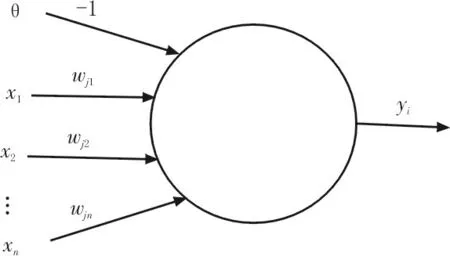
图1 神经元结构

观察神经元抽象模型可以发现，每个神经元都有自己的阈值θ，根据传递的信号是否高于阈值判断神经元是否处于兴奋状态。当传递的信号高于阈值θ时，神经元处于兴奋状态，否则神经元就处于抑制状态[5]。设神经元的输入向量及其连接权重分别为{x1,x2,…,xn} 和{wj1,wj2,…,wjn}，神经元的输出值为yi，神经元的阈值为θ，可以用以下计算公式表示神经元的输出：

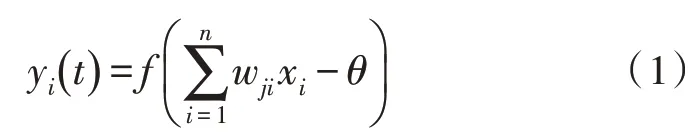
图5 为Elman 神经网络结构图，结合网络结构进行算法流程分析，Elman 神经网络有四大组成部分，分别是输入层、隐含层、承接层和输出层，其中承接层主要对隐含层信息进行存储，这一部分具有动态记忆的功能。Elman 神经网络首先对各层连接权值初始化，然后对训练数据进行归一化处理，将处理后的数据样本作为输入，传递到隐含层、输出层，接下来对实际输出和期望输出进行误差精度对比。如果输出误差不满足精度要求，则将计算值返回承接层，更新权值和阈值，并以承接层的输出作为隐含层的输入，重复之前的过程，直到输出误差满足精度要求[12]。

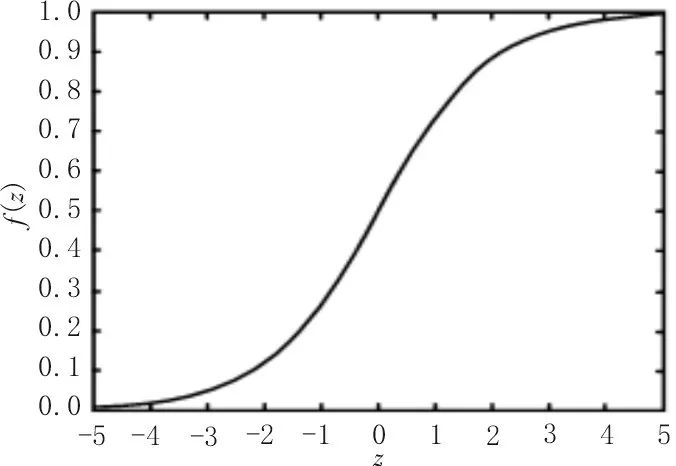
图2 sigmoid型激励函数

如果是双曲正切（tansig）型函数曲线，则激励函数表达式如下：

超声波测厚仪是根据超声波脉冲反射原理来进行厚度测量，当探头发射的超声波脉冲通过被测物体达到材料分界面时，脉冲被反射回探头。通过精确测量超声波在材料中传播的时间来确定被测材料的厚度。

在泛雅平台中将传统的“课堂教学结合多媒体”教学模式，过渡到“MOOC—学生自主学习—开放式自学方式”的模式。将学生转移为教学中心的指导思想，通过平台实施“学+做”模式。通过“精讲多练”的形式调动学生对学习的积极性，提高教学效率且强化实践教学、提高教学质量。即上课实验合并在富媒体教学中同步进行，增加基于网络信息传播的自主教学。[4]

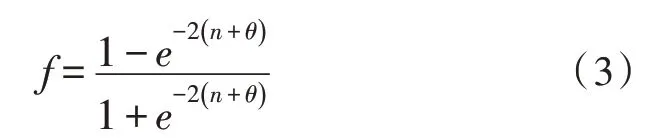
人工神经网络的实质是对人脑思维活动的模拟，组成它的每个神经元都具有不同的功能和结构，不同神经元相互交叉作用，最终得到数据处理结果[6]。不同类型的人工神经网络模型，其学习规则也各不相同，其中应用较为广泛的是δ学习规则，又称梯度法或最速下降法。假设初始权值为ω(t)，学习率为η，权值的修正方向为Δω(t)，δ学习规则的权值修正公式如下：

如果是对数（logsig）型函数曲线，则激励函数表达式如下：

前馈神经网络的信号传播是单向固定的，属于静态网络。反馈神经网络具有动力学特征，属于动态网络。在电力系统的运行中，电力负荷处于不断变化的状态，因此电力负荷预测是一个动态的系统，BP 神经网络作为典型的前馈神经网络，是静态网络模型，因此用它进行电力负荷预测，不能准确地反映电力负荷中的动态特性[9]。Elman 神经网络算法是目前应用较多的动态型神经网络，该算法的结构是由BP 神经网络结构改进而来的。改进的主要措施是在隐含层和输出层之间增加了承接层，用于隐含层输出信息的记忆存储，并作为隐含层的输入信号进行再次输入。这种方式建立起对隐含层内部的反馈，从而使得输入和输出上有了延迟传递，相当于增加了一个延时算子，运算过程以动态方程进行描述[10]。Elman 神经网络主要依据输入和输出构建网络数学模型，不需要预先设定数学模型的形式，输入信号决定了反馈的初始状态，因此，Elman 神经网络算法的关键在于选取设定合理的网络结构和连接权值[11]。

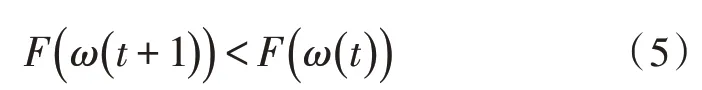
对F(ω(t+1))进行一阶泰勒展开，可以得到下述方程：

小龙是我们班出了名的个性要强又很自负的学生，他很聪明，数学成绩从没低过95分，但他爱斤斤计较、以自我为中心，脾气暴躁、满口粗话，又爱欺负同学，大家对他敬而远之。我也常被他弄得焦头烂额。借着学校“访万家”活动，我早早安排了去他家的行程。

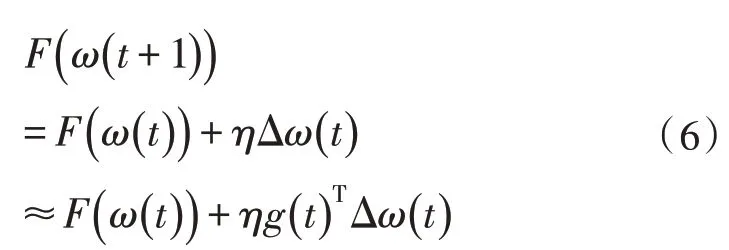
其中，g(t)=∇F(ω(t))|ω=ω(t)，在ω=ω(t)时，g(t)为F(ω)的梯度矢量。要使式（5）成立，则需要满足如下公式，此时收敛速度最快。

1.2 BP神经网络

人工神经网络根据互联方式的类型不同，可以分为反馈神经网络、前馈神经网络和自组织神经网络。前馈神经网络的结构如图3 所示，这种网络的信号传输由输入层逐层向前，各层之间没有向后的反馈信号[7]。

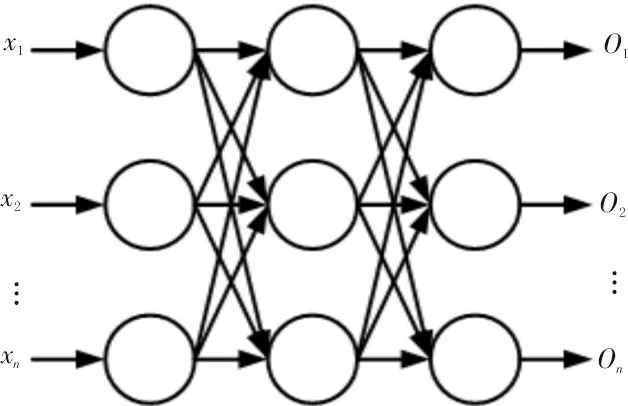
图3 前馈神经网络结构图

BP 神经网络是一种典型的前馈神经网络，这种算法在输出结果和期望值比较后，会将结果误差向隐含层反传播，并对权值系数不断调整，因此BP 神经网络算法的学习过程有两个部分，分别是信号的正向传播和误差的反向传播[8]。BP 神经网络的网络结构图在前馈神经网络结构中已有介绍，如图4 所示，将BP 神经网络的学习过程以流程图的方式进行说明。BP 神经网络在得到实际输出和期望输出的误差后，需要判断误差精度是否达到要求，若精度不够，则进行误差反向传播过程，自输出层逐层计算输出误差，并对各层神经元的权值及阈值进行修正，通过这种循环的学习调整，直到误差精度满足要求，则可以输出最终结果。

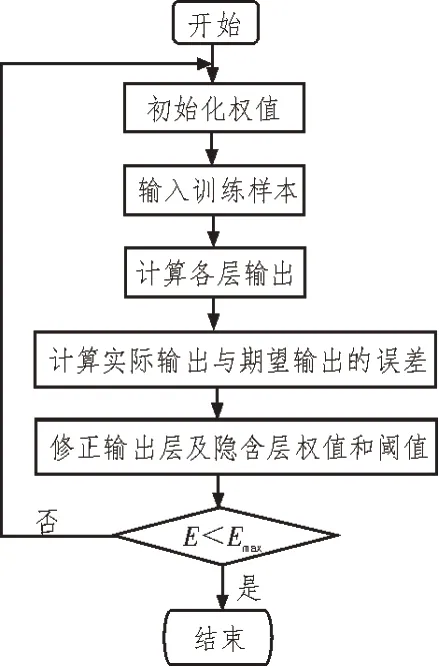
图4 BP神经网络算法学习流程

2 Elman神经网络模型及算法优化

2.1 Elman神经网络算法

这里以极小化标量函数F(ω)作为权值修正目标，为了提高收敛速度，每次修正都需要满足下述关系式：

在神经元的抽象模型中，每一个神经元节点都有其特定的激励函数，它是神经网络的核心，与神经网络处理问题的能力密切相关。sigmoid 型激励函数的特点在于任意输入值都在（0,1）范围内，且函数以双曲正切（tansig）或者对数（logsig）类似的S 形曲线进行表达，图2 为它的函数图像表达。

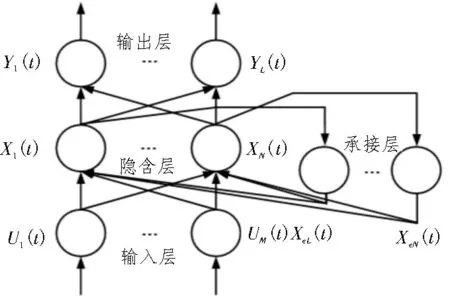
图5 Elman神经网络结构图

由于承接层的存在，系统可以通过前馈区域对连接权值进行多次修正。假设a为自连接反馈增益因子，w1、w2、w3分别表示承接层到隐含层、输入层到隐含层、隐含层到输出层之间的连接权值，隐含层和输出层的激励函数分别用f(x)和g(x)表示。下述公式为Elman 神经网络数学模型的函数表示：

反应堆压力容器属于一级安全设备,在各种运行工况和试验条件下均要保持结构的完整性，不会发生放射性物质的泄漏[1-2]。压力容器承受包括压力、热膨胀等复杂载荷，它的密封性是保证核电站安全运行的关键因素之一[3-4]。因此对其密封性进行系统深入地研究具有重要的工程意义。

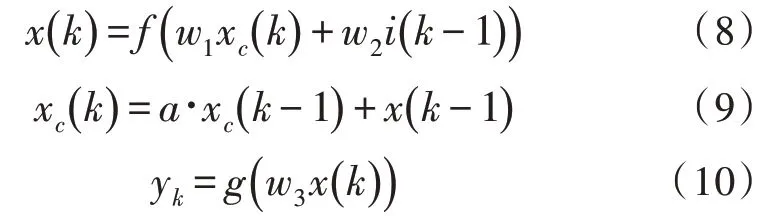
Elman 神经网络的误差函数如式（11）所示：

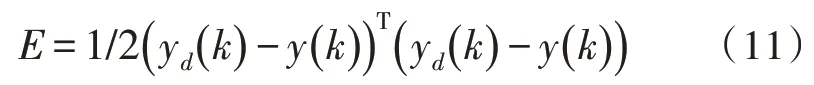
Elman 神经网络算法的关键技术在于输出层到输入层的反向调节，依据输出误差对权值和阈值不断进行修正，使其在动态预测过程中更好地控制预测精度[13]。模型采用的是最速下降法，这种方法虽然最终可以得到稳定解，但是存在不足之处，一是最速下降法容易在训练过程中陷入局部极小值；二是这种方法的学习步长是固定的，因此在面对大量数据和复杂逻辑问题时，训练效率将受到限制；三是这种方法的训练过程中存在震荡现象，对获取全局最优解形成障碍[14]。基于Elman 神经网络的上述不足之处，这次研究从两个方面加以改进，一方面是以非线性阻尼最小二乘法代替最速下降法，另一方面是对Elman 神经网络的激励函数进行改进。

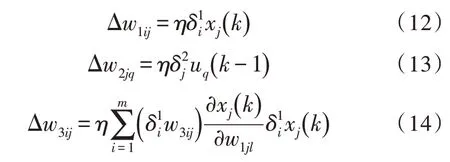
通过上述公式可以进行权值更新以及输出误差的计算，直到输出误差满足精度要求。

2.2 学习算法与激励函数优化措施

以误差对w1、w2、w3进行偏导求解，并依据进行计算，可以得到下方的关系式，其中η为学习速率。

误差函数的梯度通过式（16）进行计算，e表示误差向量。

非线性阻尼最小二乘法在对权值和阈值的修正中采用近似二阶训练速率，从而避免了Hessian 矩阵计算，由于以平方和误差形式表示误差性能函数，因此可以用下述表达式对Hessian 矩阵进行近似表示，其中，H表示包含误差函数对阈值和权值一阶导数的雅克比矩阵。

以LM 算法对Hessian 矩阵的近似表达式进行修正，可以得到式（17）。当μ为0 时，该式表示拟牛顿法；随着μ值的增加，则其逐渐变为梯度下降法[15]。根据上述分析，此次研究需要使得该式接近拟牛顿法，即系数μ随着迭代次数的增加而不断减小，从而保证最小误差的逼近效率更高，迭代后的误差性能逐渐减小。

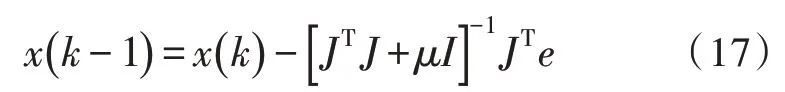
Elman 神经网络算法采用sigmoid 函数作为激励函数，但是这种函数容易陷入局部极小值，导致收敛速度下降，这里对sigmoid 函数进行改进，改进后的函数如式（18）所示：

对改进后的激励函数进行一阶求导，导函数如式（19）所示，其中，h为斜率，m、n为常数，表示函数在x轴方向和y轴方向的位移。激励函数的导函数与学习速率呈正相关关系，随着导函数值的增加，学习速率加快[16]。随着误差函数的调整，对m、n、h三者进行配合修正，从而可以优化算法的预测精度和收敛速度。

随着信息技术在初中音乐课堂中的普及，各种各样新型的教学模式不断涌现，情境教学法作为其中较为突出的一种，得到了越来越多教育工作者的关注，它能根据教学内容设计相应的学习情境，将抽象的理论知识点形象化、具体化，在降低了知识点理解难度的同时也提高了课堂教学趣味性，有效激发了学生的音乐学习兴趣。教师要发挥情境教学法的优点，根据音乐教学需求调整设计方案，保证学生在情境中德智体美的全面发展。

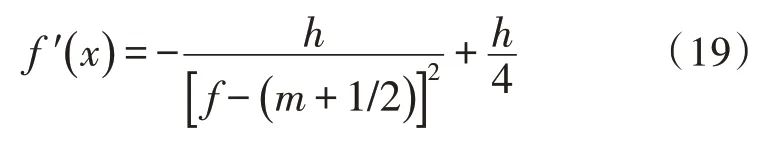
3 短期电力负荷预测的仿真分析

为了对优化后的Elman 神经网络模型进行验证，选取M 电力企业在2 月份按日采集的24 小时电力负荷数据作为研究对象，以同一天的电力负荷数据为一组，将所有数据分为24 组。以前三天的数据为输入数据，后一天的数据为期望输出，对算法进行循环训练，该过程在MATLAB 仿真环境下进行。选择优化后的Elman 神经网络算法和传统BP 神经网络算法进行仿真分析对比，其中Elman 神经网络的网络结构采取双隐含层结构，该结构在多输入的情况下可以有效地提高预测精度和收敛速度。通过前期实验对预测效果的对比，确定Elman神经网络的两个隐含层节点分别为14个和12个。

2．2 ELISA检测各组小鼠血清IGF－1水平 A组血清IGF－1呈较低水平，B组血清IGF－1水平明显高于A组，C组血清IGF－1水平较B组降低，但仍较A组高。各组差异有统计学意义（P＜0．05）。见表1。

图6 表示BP、Elman 神经网络模型预测输出与实际输出对比，观察图中的3 条曲线走势可以发现，BP 神经网络预测输出值的整体走势与电力负荷走势大致契合；但Elman 神经网络模型预测输出值明显优于BP 神经网络模型，并且在Elman 神经网络模型的MATLAB 仿真实验中，算法模型在52 次训练后，收敛效率、输出误差精度取得了较好的效果。将模型预测值减去实际输出值，得到预测误差值，如表1 所示。

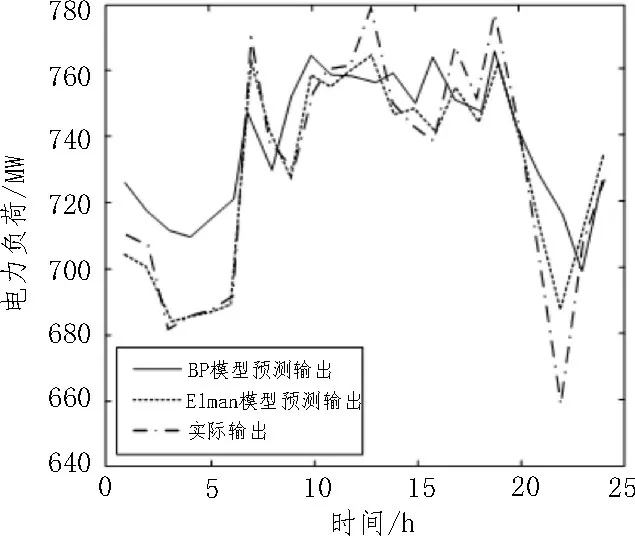
图6 预测输出与实际输出对比

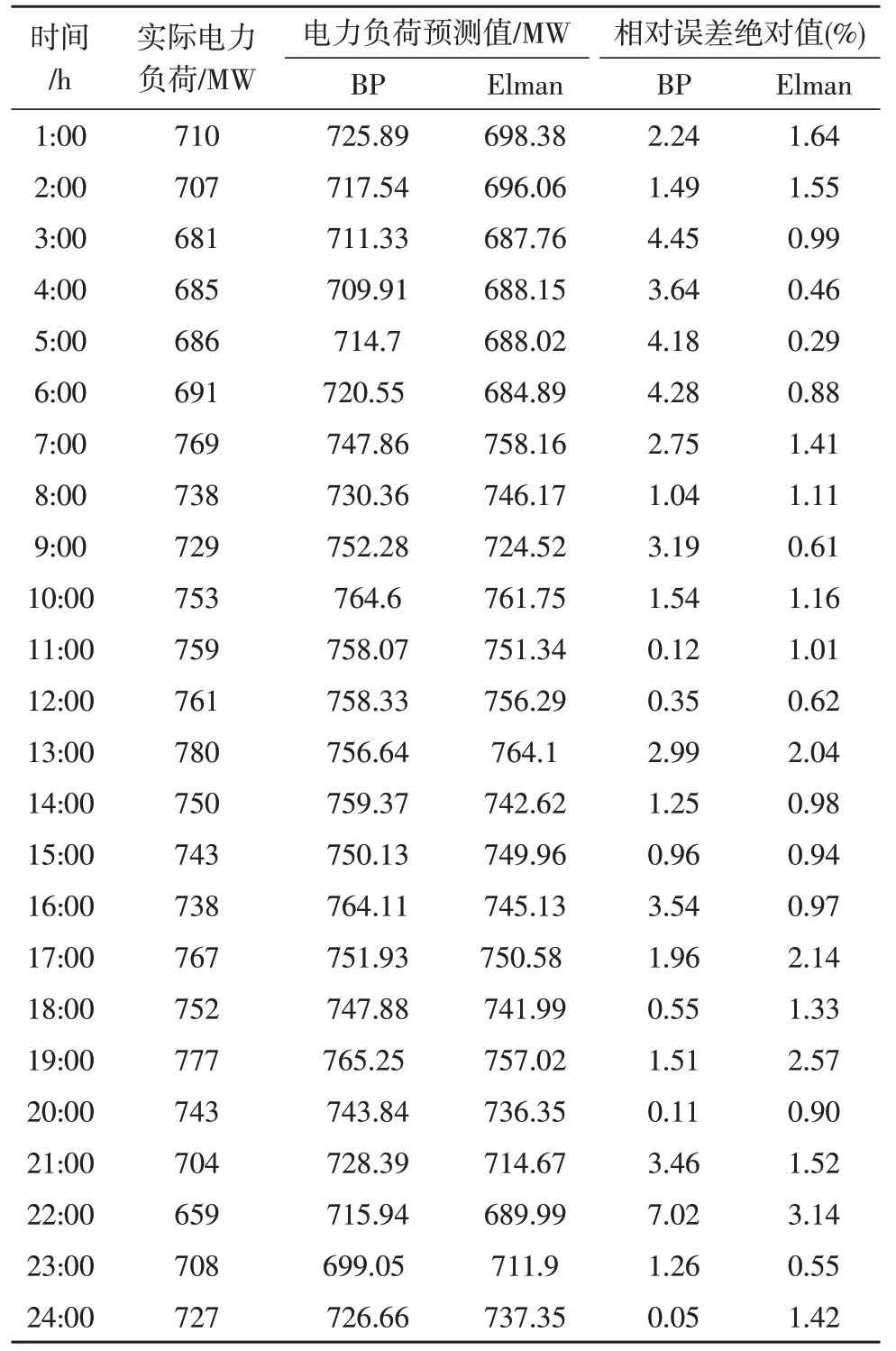
表1 模型预测的相对误差对比

观察表1 中的预测误差数据可以发现，BP 神经网络的相对误差绝对值基本在4.45%以内，Elman神经网络的相对误差绝对值基本在2.57%以内；22∶00 时的数据预测误差存在明显波动，BP 神经网络和Elman 神经网络在同一时点的相对误差绝对值分别是7.02%和3.14%，分析此处数据可能存在异常情况影响。根据相对误差绝对值，对BP 神经网络和Elman 神经网络在不同时点的预测精度进行对比，结果如表2 所示，在BP 神经网络模型下，输出预测值的平均预测精度为97.75%；在Elman 神经网络模型下，输出预测值的平均精度为98.74%，取得了较为满意的结果。

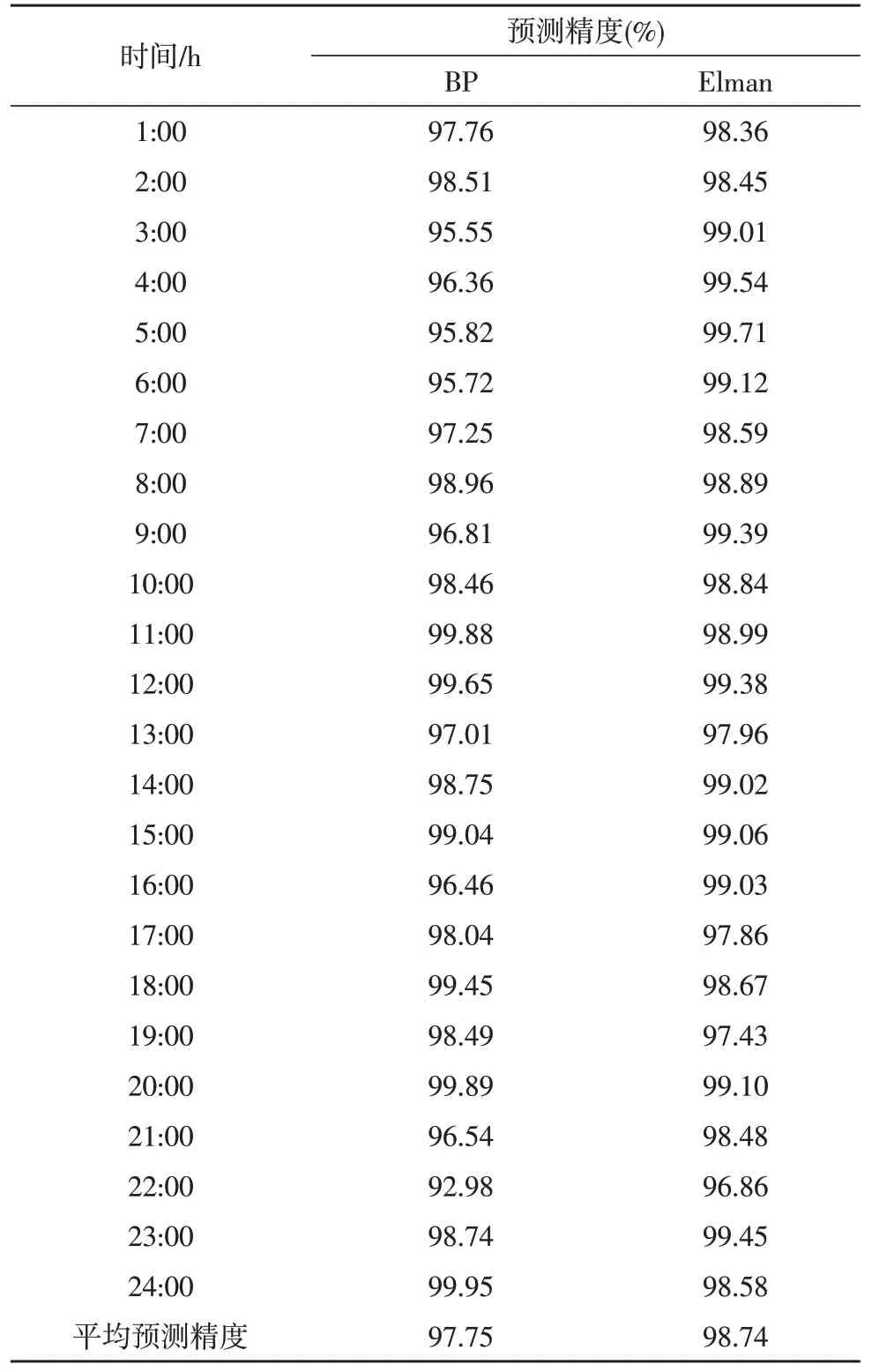
表2 模型预测精度对比

4 结束语

电力产业已经成为国家经济的支柱型产业，电力负荷预测的精度对电网运行的稳定性和安全性有着重要影响。针对传统电力负荷预测方法中的不足之处，此次研究将以静态神经网络和动态神经网络对短期电力负荷进行预测，从学习规则和激励函数方面进行算法优化，并以BP 神经网络和Elman 神经网络这两种类型的典型代表算法进行仿真实验对比。预测数据变化趋势显示，BP 神经网络预测输出值的整体走势与电力负荷走势大致契合；但Elman神经网络模型预测输出值明显优于BP 神经网络模型，并且在Elman 神经网络模型的MATLAB 仿真实验中，算法模型在52 次训练后，收敛效率、输出误差精度取得了较好的效果。算法的预测精度对比显示，在BP 神经网络模型下，输出预测值的平均精度为97.75%；在Elman 神经网络模型下，输出预测值的平均精度为98.74%。在这次的研究中，Elman 神经网络算法应用于短期电力负荷预测，取得了良好的预测效果，这证明在动态问题的处理上，Elman 神经网络算法优于BP 神经网络算法。但研究尚且存在不足之处，如预测算法的初始权值是随机选取的，这说明此次研究所提出的算法还有进一步优化的空间。