城市轨道交通客流短时预测方法研究

熊 洋，李淑庆，许 浩，刘 怡

（1.重庆交通大学 交通运输学院，重庆 400074；2.西南交通大学交通运输与物流学院，四川成都 610097）

随着我国城市交通建设的推进，轨道交通的优势愈加明显，虽然这种交通方式在很大程度上缓解了地面交通压力，避免了高峰期交通堵塞等问题，但是它在使用中也存在一些问题。例如，不同换乘枢纽的客流拥挤程度不同，客流量在不同时间段呈现出阶段性变化等[1]。当客流量急剧增加时，需要增加列车数量或发车次数，以缓解运营压力；当客流量减小时，需要减少列车数量或发车车次来控制交通运营成本[2]。对轨道交通的客流量进行预测，有助于提高轨道交通的运营效率和资源调度能力[3]。考虑到轨道交通客流量的短时预测具有高度的非线性和不确定性，这次研究在BP 神经网络的基础上进行改进，分别以LM 算法和GA 算法提升预测效率和预测精度，旨在为城市轨道交通运营提供有价值的参考。

1 客流短时预测的LM-BP算法改进

BP 神经网络作为典型的前馈神经网络，它会根据实际输出值与期望输出值的输出误差，逐层反向调整输出层到隐含层的权值，因此它的学习过程包括正向传播和反向传播两个部分[4-5]。图1 为BP 神经网络的结构。

设BP 神经网络的输入值为xn，实际输出值为Om，通过计算得到的期望输出值为Ym，m、n、p分别表示输出层、输入层和隐含层的节点数，则实际输出与期望输出的误差值e由式（1）得到。

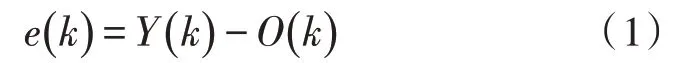
当BP 神经网络的学习速率为η时，以H表示中间输出值，网络的连接权值根据式（2）调整。

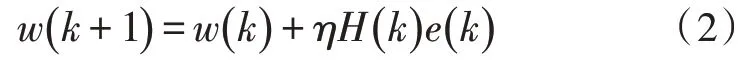
在满足网络结构要求时，BP 神经网络可以对非线性问题任意逼近，但是该方法的局限性也非常明显[6]。随着迭代次数的增加及误差的减小，算法的收敛速度下降，学习效率逐渐降低，模型梯度逐渐消失，这将严重影响预测效果[7]。有鉴于此，研究选择LM 算法对BP 神经网络进行优化。

LM 算法将高斯牛顿法和梯度下降法相结合，其误差性能函数E(k)见式（3）。

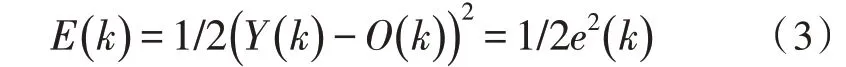
设权值的误差向量为e(w)，则误差和函数和梯度函数分别见式（4）、（5）。

在式（5）中，J为雅克比矩阵。当误差性能函数E(k)趋于最小值时，矩阵的元素可以忽略不计。因为JTJ并不总是可逆，所以这里引入微小增量μI，I表示n×n的单位矩阵，μ＞0 。LM-BP 算法的更新权值见式（6）。

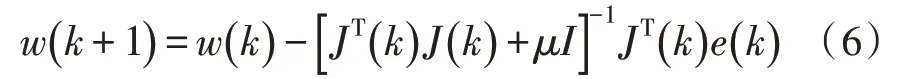
在式（6）中，JTJ恒为正，因此算法恒有解。当μ→0 时，它表示高斯牛顿法；当μ→∞时，它表示梯度下降法。LM 算法的优化思路在提高模型收敛速度的同时，降低了计算难度[8]。

2 GA算法对LM-BP预测模型的精度优化

遗传算法又称GA 算法，它结合了达尔文进化论的思想，通过模拟生物进化过程，实现对可行解的全局寻优[9]。在遗传算法中，有3 个基本概念，分别是编码、初始种群、适应度。遗传算法需要对可行解进行编码，以此产生初始种群，这一过程决定了问题的解决程度。初始种群是随机产生的，它的随机性与自然选择的思想相吻合。适应度是判断种群能否遗传的重要指标，在实际问题中，它表示目标函数的值[10-11]。在遗传算法中，种群会经过复制、交叉、变异操作，在这些操作之后，适应度高的算子得以保留，适应度低的算子被淘汰。通过算法的多次迭代，最终可以得到全局最优解。在BP 神经网络的优化中，利用遗传算法可以对初始值进行优化，属于启发式优化技术。虽然LM-BP 算法解决了BP 神经网络模型中梯度消失的问题，但是这种算法模型仍旧存在非凸优化问题，即容易陷入局部极值[12]。另一方面，与遗传算法相比，LM-BP 算法的全局寻优能力较弱。为了进一步提高模型的预测精度，这里将遗传算法与LM-BP 神经网络算法相结合，并以此构建新的预测模型。

LM-BP 神经网络通过误差的反向传播，调整网络的权值和阈值，以此得到满足要求的输出值。因此在这次的优化中，将利用遗传算法的全局寻优能力，对网络权值和阈值进行初始化操作[13]。将这一结果作为LM-BP 神经网络的初始权值和阈值，不仅极大地提高了算法的运算效率，而且保证了预测结果的全局性。在GA 遗传算法中，有两种编码方式，分别是二进制编码和实数编码。二进制编码需要解码过程，这种方式在数据操作过程中接近生物学特性。实数编码是类似自然语言的编码方式，不需要解码过程，操作过程和结果更为直观，因此这里将采用实数编码[14]。

图2 为GA 算法优化下的LM-BP 神经网络流程图。流程图分为两个部分，分别是GA 算法部分和LM-BP 神经网络部分。在GA 算法部分，首先将样本数据输入，并进行预处理操作；其次利用GA 遗传算法对初始权值和阈值进行编码，构成初始种群；然后使用蒙特卡洛法对初始种群个体进行选择，确定其遗传可能性；接下来对选择后的个体执行单点交叉操作和均匀变异操作；最后根据预测值和实际值，对处理后的数据计算适应度值，并进行判断[15]。若适应度值未能满足最大遗传，则返回上述个体选择步骤；若适应度值满足最大遗传，则可以得到一组相对最优的权值和阈值。将遗传操作所获得的权值和阈值代入LM-BP 算法模型中，计算输出层和隐含层的校正误差，并根据误差调整权值和阈值。当输出误差不满足精度要求时，则返回计算输出层和隐含层的校正误差；当输出误差满足精度要求时，则输出预测结果[16]。

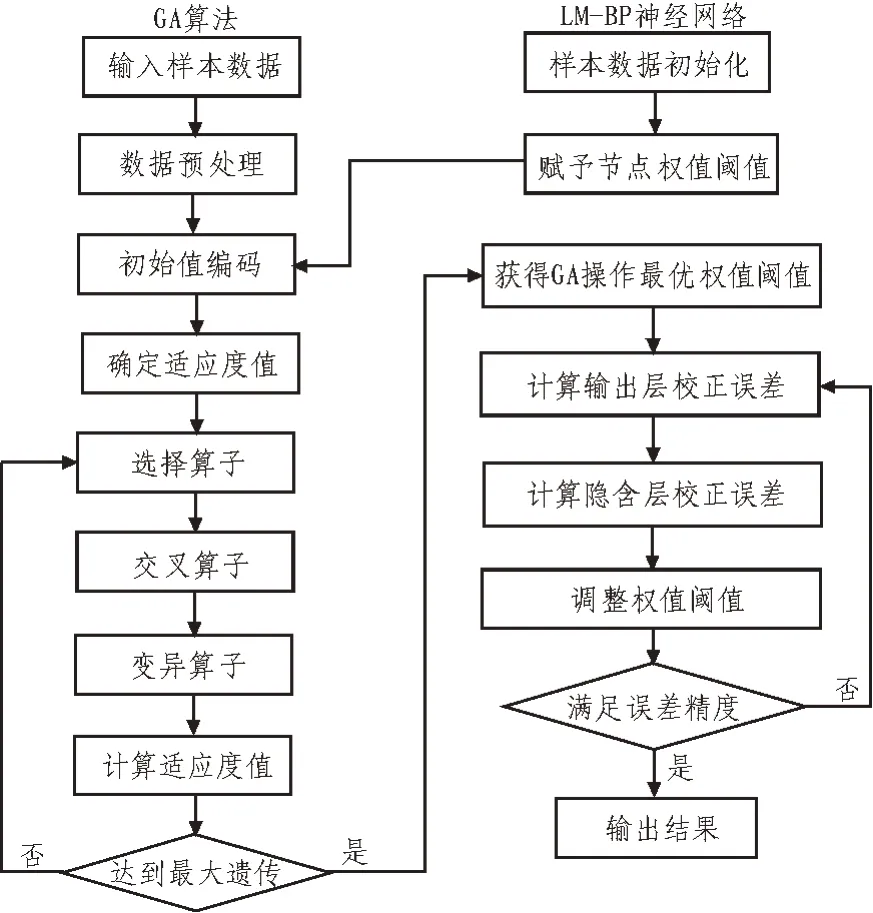
图2 基于GA算法优化的LM-BP神经网络流程图

在轨道交通的客流预测中，预测结果的准确率并不能代完全反映预测模型的性能。在预测模型的性能评价中，有相对误差、平均绝对误差、均方误差、平均绝对百分误差等评价指标[17]。这次研究将采用平均绝对误差（MAD）、平均绝对百分误差（MAPE）和均方误差（MSE）这3 个指标。在实际的模型预测中，会出现预测值为正或者负的情况。平均绝对误差是一个描述预测结果偏离程度的统计量，由于离差被绝对值化，它不会出现正负相抵的情况，因此能更好地反映预测值误差的实际情况。平均绝对百分误差是衡量预测准确程度的统计指标，它是百分比值，一般认为当MAPE＜10%时，模型的预测精度较高。均方误差是真实值与预测值之差的平方然后求和平均，与MAD 相比，MSE 可以放大预测偏差较大的值，且可以比较不同预测模型的稳定性。式（7）～（9）分别表示模型预测的平均绝对误差、平均绝对百分误差和均方误差。

3 客流预测优化模型的性能仿真

为了验证遗传算法优化的LM-BP 算法模型的预测性能，此次研究采集了S 市轨道交通的小时客流数据，并对轨道交通客流短时预测模型进行仿真测试。根据实验开展的前期数据调查发现，1 号线A站的全天客流呈现出典型双峰型特征，2 号线B 站的全天客流呈现出典型单峰型特征。在2019 年11 月进行客流数据采集，采集时间间隔为15 min，采集数据以时间序列进行反映。以最后一周的数据集作为测试集，其余数据集作为训练集，采用优化前和优化后的3 种模型进行仿真预测，并通过Matlab 平台实现。在GA-LMBP 算法中，经试验设置种群数量为120，变异概率pc=0.95，η=0.01。

图3 为不同预测模型的迭代效率统计。从图3的统计结果可以看出，BP 神经网络算法在迭代80 次前收敛速度较快，此后收敛速度明显降低，但在迭代200 次后仍旧无法满足误差精度要求；LM-BP 算法模型在迭代第4 次就已经趋于误差精度要求并逐渐稳定；GA 遗传算法在优化LM-BP 模型时，其迭代次数为65 次。由此来看，研究所提出的LM 算法和GA算法优化显著提升了BP 算法的运算效率。由于篇幅限制，这里仅展示GA-LM-BP 算法模型的相对误差统计结果。

图3 不同预测模型的迭代效率

图4 为两个站点在GA-LM-BP 模型下的预测相对误差。（a）为1 号线A 站的统计结果，GA-LM-BP算法的客流预测在前期将相对误差控制在±40%左右，随着训练数据的增加，预测的相对误差逐渐减小，最终控制在±20%的范围内。（b）为2 号线B 站的统计结果，GA-LM-BP 算法的预测相对误差控制在±10%的范围内，有少量预测值误差在±20%左右。采用相同的算法模型，两个站点的预测误差分布情况有所不同，这说明不同时间序列特征的数据集在算法模型中的预测效果不同。A 站点属于双峰型时间分布的客流特征，B 站点属于单峰型时间分布，因此A 站点数据集中的数据变化频率是B 站点的两倍。由此分析，当数据量较少时，算法模型对A站点的预测难度增加；随着数据量的增加，预测精度逐渐提高。另一方面，B 站点的预测中存在少量的噪声影响，这可能是由于样本数据量不够，降低了算法模型的预测精度。

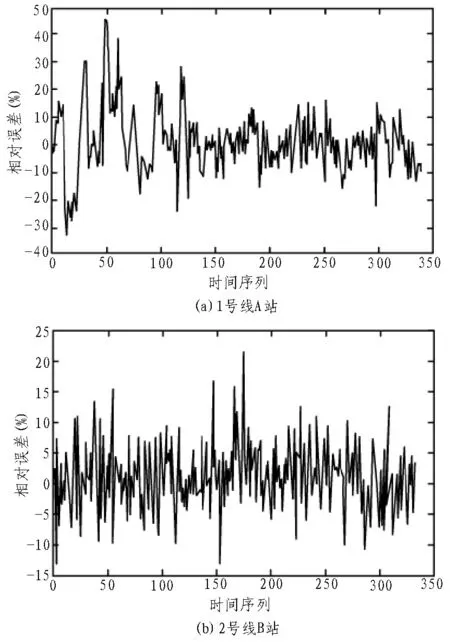
图4 GA-LM-BP算法预测的相对误差统计结果

表1 为轨道交通客流短时预测模型的性能统计结果。根据表1 的统计结果可以发现，在1 号线A 站的客流预测中，采用LM 算法优化BP 算法模型，模型的MAD 值、MAPE 值、MSE值分别减小了131.55、23.42%、113.89；采用GA 算法优化LM-BP 算法模型，模型 的MAD 值、MAPE 值、MSE值分别减小了7.86、1.73%、12.91。在2 号线B 站的客流预测中，采用LM 算法优化BP 算法模型，模型的MAD 值、MAPE值、MSE 值分别减小了45.33、11.04%、36.78；采用GA 算法优化LM-BP 算法模型，模型的MAD 值、MAPE 值、MSE 值分别减小了1.46、0.43%、1.04。根据统计结果可知，GA-LM-BP 算法模型的MAD 值最小，这说明模型预测结果与真实值之间的偏差最小；BP 算法模型的MAD 值最大，这说明BP 算法的预测结果与真实值存在较大偏差。在MAPE 值的计算结果中，BP 算法模型的评价结果大于10%，无法满足预测模型的精度要求；LM-BP 算法模型和GA-LMBP 算法模型的评价结果均小于10%，且后者小于前者，这说明两种优化方式均达到了预测模型的精度要求，且GA-LM-BP 算法模型的预测精度更高。在MSE 的评价结果中，GA-LM-BP 算法模型的评价值最小，BP 算法模型的评价值最大，这说明前者的预测模型稳定性优于后者。整体而言，LM 算法对BP神经网络的优化效果十分显著，GA 算法则进一步提高了LM-BP 算法模型的预测精度和稳定性。

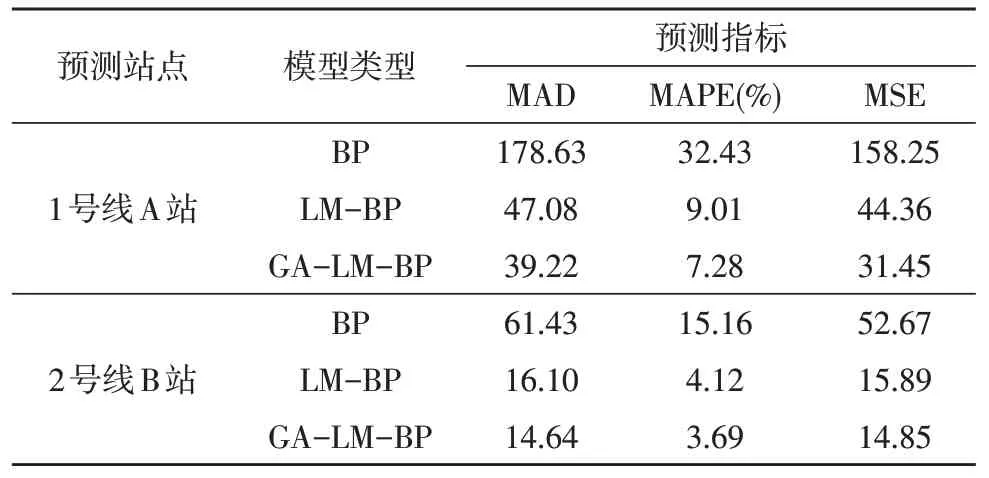
表1 轨道交通客流短时预测模型的性能统计结果

4 结论

城市人口的增加向城市交通运营提出了挑战，而轨道交通极大地缓解了城市交通的运营压力，是目前很多城市的发展重点。这次研究提出了轨道交通的短时客流预测模型，并采用LM 算法和GA 算法对BP 神经网络预测模型进行优化。为了验证优化模型的有效性，研究采用S 市客流实测数据进行仿真实验，并对预测模型的性能进行评价。研究结果显示，在GA 算法和LM 算法两者的优化下，A 站点预测 结果 的MAD 值、MAPE值、MSE值分别减小了139.41、25.15%、126.80，B 站点预测结果的MAD 值、MAPE 值、MSE 值分别减小了46.79、11.47%、37.82。研究结果说明优化模型的预测精度和稳定性有了大幅提高，优化模型在客流短时预测上具有良好的适用性。这次研究为轨道交通的客流短时预测提供了新的优化思路和数据参考，但研究尚且存在不足之处，如对于具有不同时间分布特征的客流数据，未能对其在模型预测上的影响进行深入研究，这将在后续工作中作出改进。