Reduced-dimension Target Parameter Estimation For Conformal FDA-MIMO Radar

CHEN Hui TIAN Xiang LI Zihao JIANG Xinrui

(School of Information and Communication Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)

Abstract:Frequency Diverse Array (FDA) Multiple-Input Multiple-Output (MIMO) radar equipped with a FDA can possess beam patterns that are dependent on range,angle,and time,and it can increase the degree of freedom.This paper introduces a conformal array attached to the surface of the carrier,the array can reduce the aerodynamic impact on the carrier and reduce the cross section of the FDA-MIMO radar.First,the conformal FDA-MIMO measurement model is formulated,and a Cramér-Rao Lower Bound (CRLB) is derived to evaluate the parameter estimation performance.To avoid the three-dimensional search of the traditional three-dimensional MUltiple SIgnal Classification (3D-MUSIC) algorithm,a Reduced-Dimension MUltiple SIgnal Classification (RD-MUSIC) algorithm is proposed for parameter estimation.The simulation results demonstrate that the proposed algorithm has a slightly lower estimation accuracy than the 3D-MUSIC algorithm but a much lower computational complexity.In addition,the proposed algorithm has better range estimation performance for multiple targets than the 3D-MUSIC algorithm.

Key words:Conformal array;FDA-MIMO;Parameter estimation;3D-MUSIC;RD-MUSIC

1 Introduction

In recent years,Frequency Diverse Array(FDA) radar has received much attention due to its range-angle-time-dependent beampattern[1,2].Combining the advantages of FDA and traditional phased array Multiple-Input Multiple-Output(MIMO) radar in the degree of freedom,the FDA Multiple-Input Multiple Output (FDA-MIMO)radar was proposed in Ref.[3] and applied in many fields[4–9].For parameter estimation algorithm,the authors first proposed a FDA-MIMO target localization algorithm based on sparse reconstruction theory[10],and an unbiased joint range and angle estimation method was proposed in Ref.[11].The work of Ref.[12] further proved that the FDA-MIMO is superior to traditional MIMO radar in range and angle estimation performance,and the authors of Ref.[13] introduced a super-resolution MUSIC algorithm for target location,and analyzed its resolution threshold.Meanwhile,high-resolution Doppler processing is utilized for movingtarget parameter estimation[14].The Estimation of Signal Parameters via Rotational Invariance Technique (ESPRIT) and PARAllel FACtor (PARAFAC) was proposed in Ref.[15],which is a search-free algorithm for FDA-MIMO.

Moreover,the research of conformal array has received more and more attention.Conformal array is a non-planar array that can be completely attached to the surface of the carrier[16].It has significant advantages such as reducing the aerodynamic impact on the carrier and smaller radar cross section[17].In addition,conformal array can achieve wide-angle scanning with a lower SideLobe Level (SLL)[18].Different from traditional arrays,the element beampattern of conformal array needs to be modeled separately in the parameter estimation due to the difference of carrier curvature[19–21].

As far as we know,most of the existing researches on FDA-MIMO are based on linear array,while there is little research on the combination of FDA-MIMO and conformal array[22].In this paper,we replace the receiving array in the traditional FDA-MIMO with conformal array.Compared with conventional FDA-MIMO,conformal FDA-MIMO inherits the merits of conformal array and FDA-MIMO,which can effectively improve the stealth and anti-stealth performance of the carrier,and reduce the volume and the air resistance of the carrier.For conformal FDA-MIMO,we further study the parameters estimation algorithm.The major contributions of this paper are summarized as follows:

(1) A conformal FDA-MIMO radar model is first formulated.

(2) The parameter estimation Cramér-Rao Lower Bound (CRLB) for conformal FDA-MIMO radar is derived.

(3) Inspired by the existing work of Refs.[23,24],a Reduced-Dimension MUSIC (RD-MUSIC) algorithm for conformal FDA-MIMO radar is correspondingly proposed to reduce the complexity.

The rest of the paper consists of four parts.Section 2 formulates the conformal FDA-MIMO radar model,and Section 3 derives a RD-MUSIC algorithm for conformal FDA-MIMO radar.Simulation results for conformal FDA-MIMO radar with semi conical conformal receiving array are provided in Section 4.Finally,conclusions are drawn in Section 5.

2 Conformal FDA-MIMO Radar

2.1 General conformal FDA-MIMO signal model

For the convenience of analysis,we consider a monostatic conformal FDA-MIMO radar which is composed by aM-element linear FDA transmitting array and aN-element conformal receiving array,as shown in Fig.1.ddenotes the interelement spacing,the carrier frequency at themth transmitting element isfmf1+Δf(m −1),m1,2,...,Mwheref1is the transmission frequency of the first antenna element,which is called as reference frequency,and Δfis the frequency offset between the adjacent array elements.

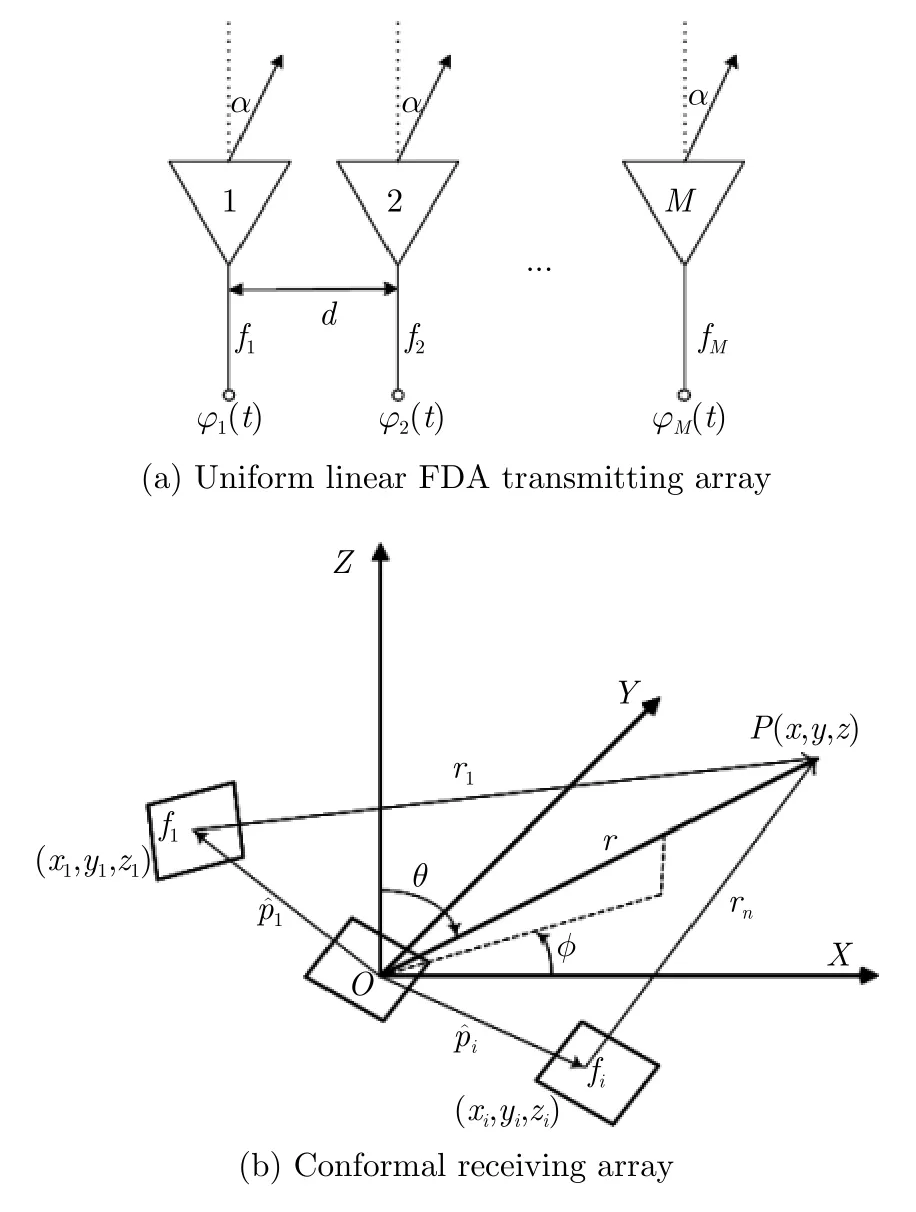
Fig.1 Conformal FDA-MIMO radar

The complex envelope of the transmitted signal of themth transmitting element is denoted asφm(t),assume the transmitting waveforms have orthogonality,

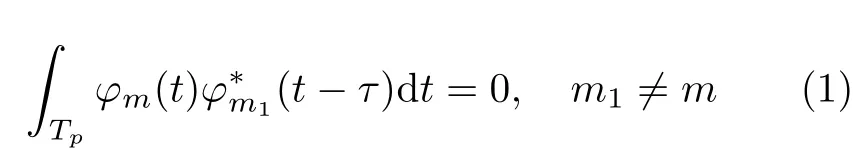
whereτdenotes the time delay,Tpdenotes the pulse duration,and (·)∗is conjugate operator.The signal transmitted from themth element can be expressed as

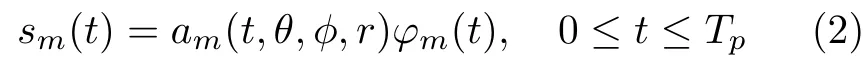
where

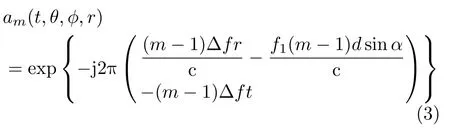
is themth element of the transmitting steering vector according to the phase difference between adjacent elements,the angle between far-field target and transmitting array is denoted asαarcsin(sinθcosφ),where a rcsin(·) denotes arcsine operator,αcan be calculated by using the inner product between the target vector and unit vector along theX-axis.θ,φ,rare the elevation,azimuth and range between the target and the origin point,respectively.The phase difference between adjacent elements is

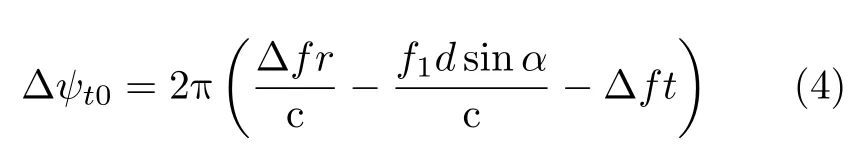
where c is light speed.For far-field targetP(r,θ,φ),the transmitting steering vector is

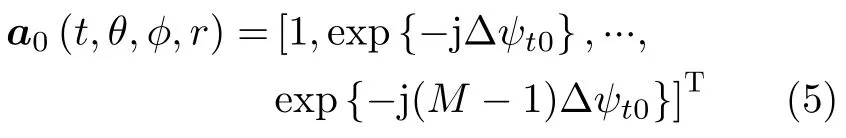
For the conformal receiving array,as shown in Fig.1(b),the time delay between targetP(r,θ,φ) and thenth receiving array element is

wherernis the range between target and thenth receiving array element.For far-field assumption,therncan be approximated as

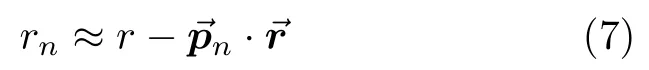
whererdenotes the range between the target and the origin point,xnex+yney+znezdenotes the position vector from thenth element to origin point,andsinθcosφex+sinθsinφey+cosθezis the unit vector in target orientation,whereex,eyandezare the unit vectors along theX-,Y-,andZ-axis,respectively.(xn,yn,zn) are the coordinates of thenth element in the Cartesian coordinate system.For simplicity,we letusinθcosφ,vsinθcosφ,so the time delayτn(r −(uxn+vyn+cosθzn))/c.The time delay between the first element and thenth element at the receiving array is expressed as

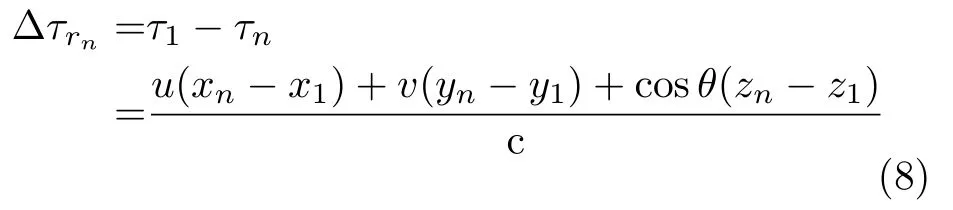
And the corresponding phase difference between the first element and thenth element is

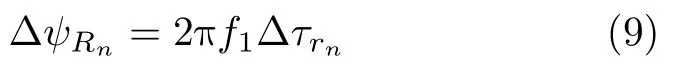
Consequently,the receiving steering vector is

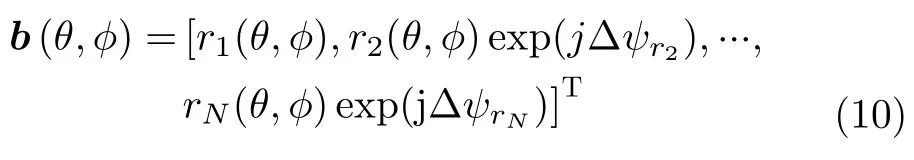
wherern(θ,φ) is thenth conformal receiving array element beampattern which should be designed in its own local Cartesian coordinate system.In this paper,we utilize Euler rotation method to establish transformation frame between local coordinate system and global coordinate system[25,26].

Then the total phase difference between adjacent transmitting array elements can be rewritten as

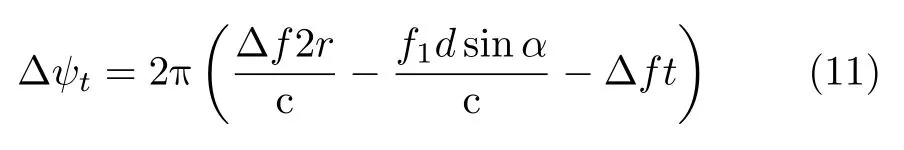
where the factor 2rin the first term represents the two-way transmission and reception,and the correspondingly transmitting steering vector is written as

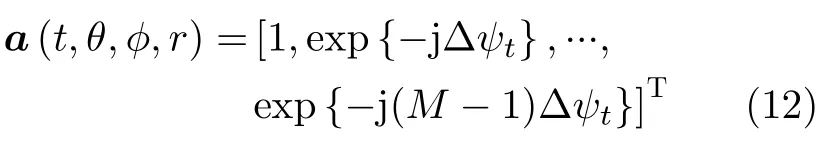
AssumingLfar-field targets are located at(θi,φi,Ri),i1,2,...,Land snapshot number isK.After matched filtering,the received signal can be formulated as following matrix (13,14)

where the array manifoldAis expressed as

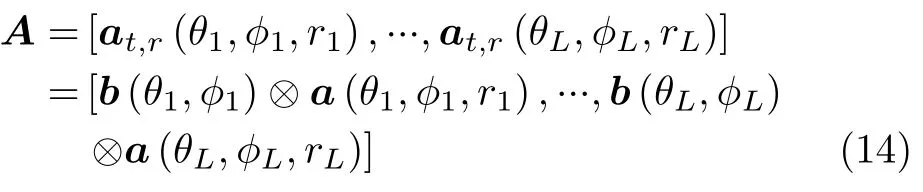
whereat,r(θ,φ,r) is the joint transmitting-receiving steering vector,S[s(t1),s(t2),...,s(tK)]∈CL×KandN ∈CMN×Kdenote the signal matrix and noise matrix,respectively,where noise follows the independent identical distribution,and⊗denotes Kronecker product.

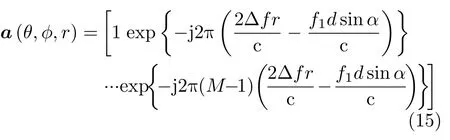
which can be expressed as

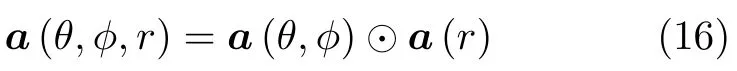
where

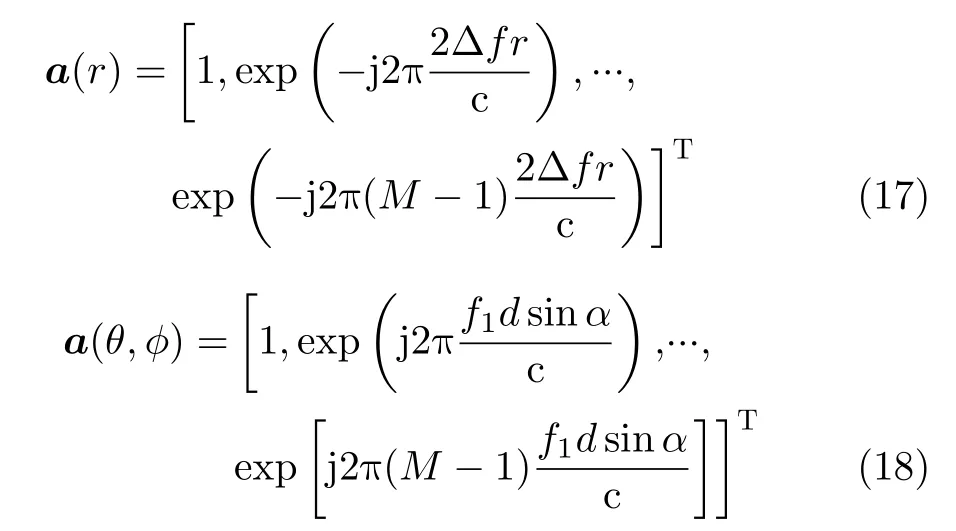
and⊙represents Hadamard product operator.

2.2 CRLB of conformal FDA-MIMO

The CRLB can be obtained from the inverse of Fisher information matrix[27,28],which establishes a lower bound for the variance of any unbiased estimator.We employ the CRLB for conformal FDA-MIMO parameter estimation to evaluate the performance of some parameter estimation algorithms.

The discrete signal model is

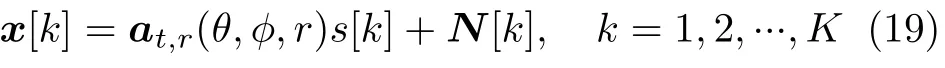
For the sake of simplification,we takeat,ras the abbreviation ofat,r(θ,φ,r).

The Probability Distribution Function (PDF)of the signal model withKsnapshots is

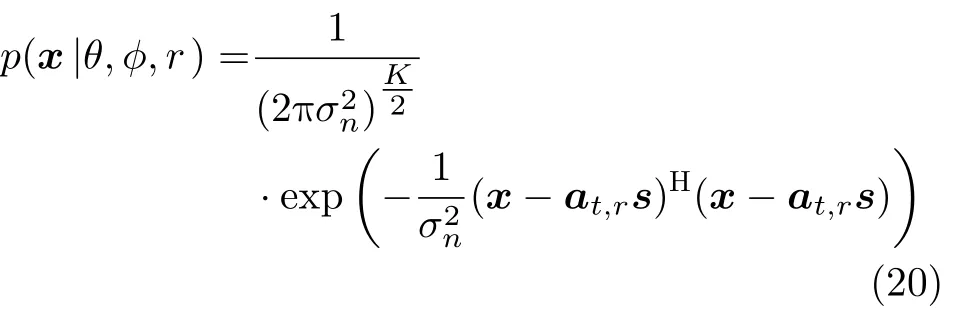
wherex[x(1),x(2),...,x(K)] ands[s(1),s(2),...,s(K)].

The CRLB matrix form of elevation angle,azimuth angle and range is given by Eq.(21),diagonal elements{Cθθ,Cφφ,Crr}represent CRLB of estimating elevation angle,azimuth angle and range,respectively.

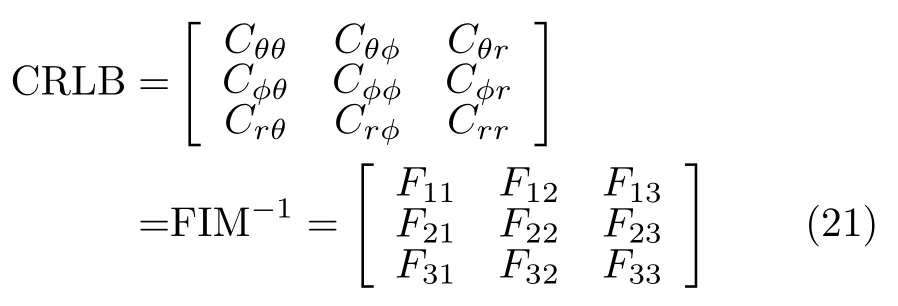
The elements of Fisher matrix can be expressed as

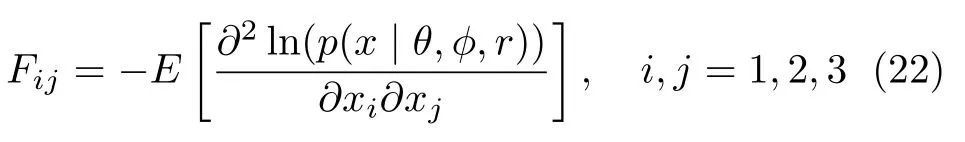
In the case ofKsnapshots,PDF can be rewritten as

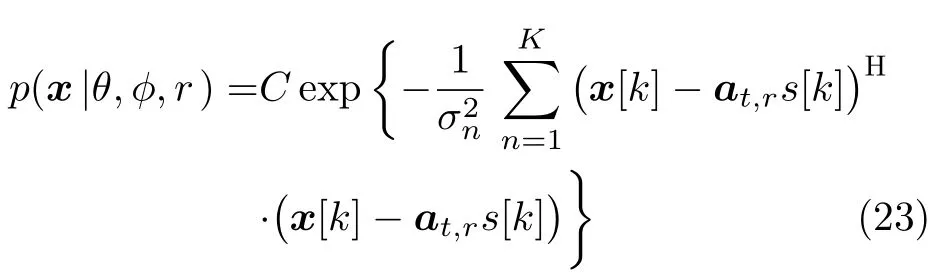
whereCis a constant,natural logarithm of Eq.(23) is

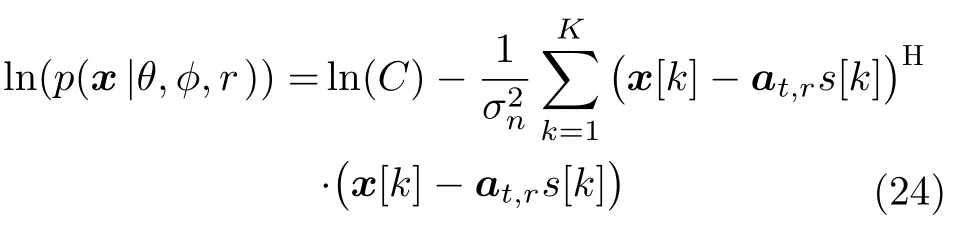
where l n(·) represents the logarithm operator.The first entry of Fisher matrix can be expressed as

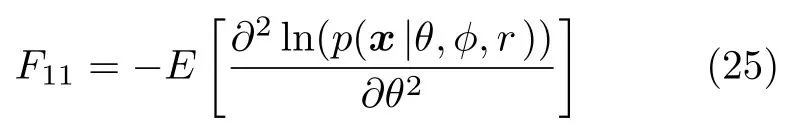
Correspondingly,the first derivative of natural logarithm is given by

Then we can obtain the second derivative of

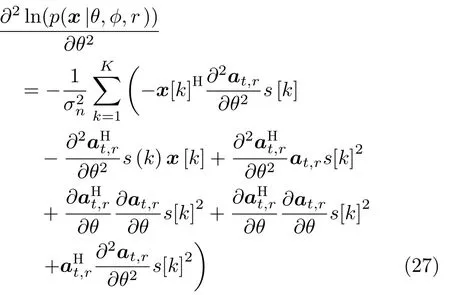
And then we have

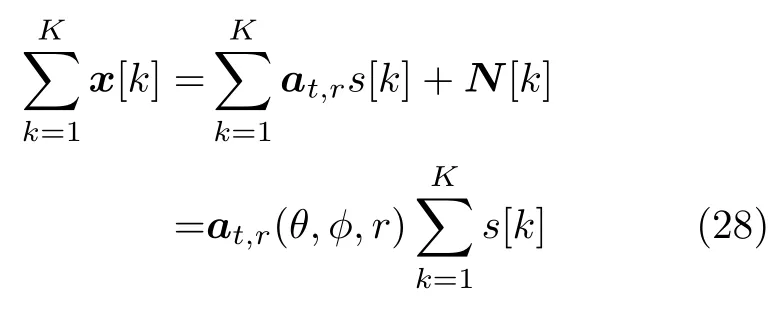
and

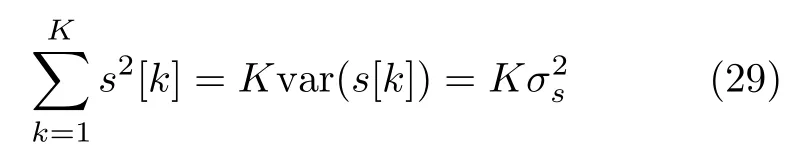
where var(·) is a symbol of variance.Therefore,the PDF after quadratic derivation can be written as

where‖·‖denotes 2-norm.Similarly,the other elements of the Fisher matrix can also be derived in the similar way,so the Fisher matrix can be expressed as

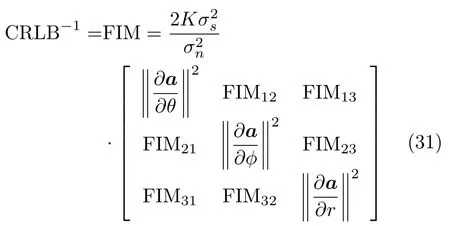
where

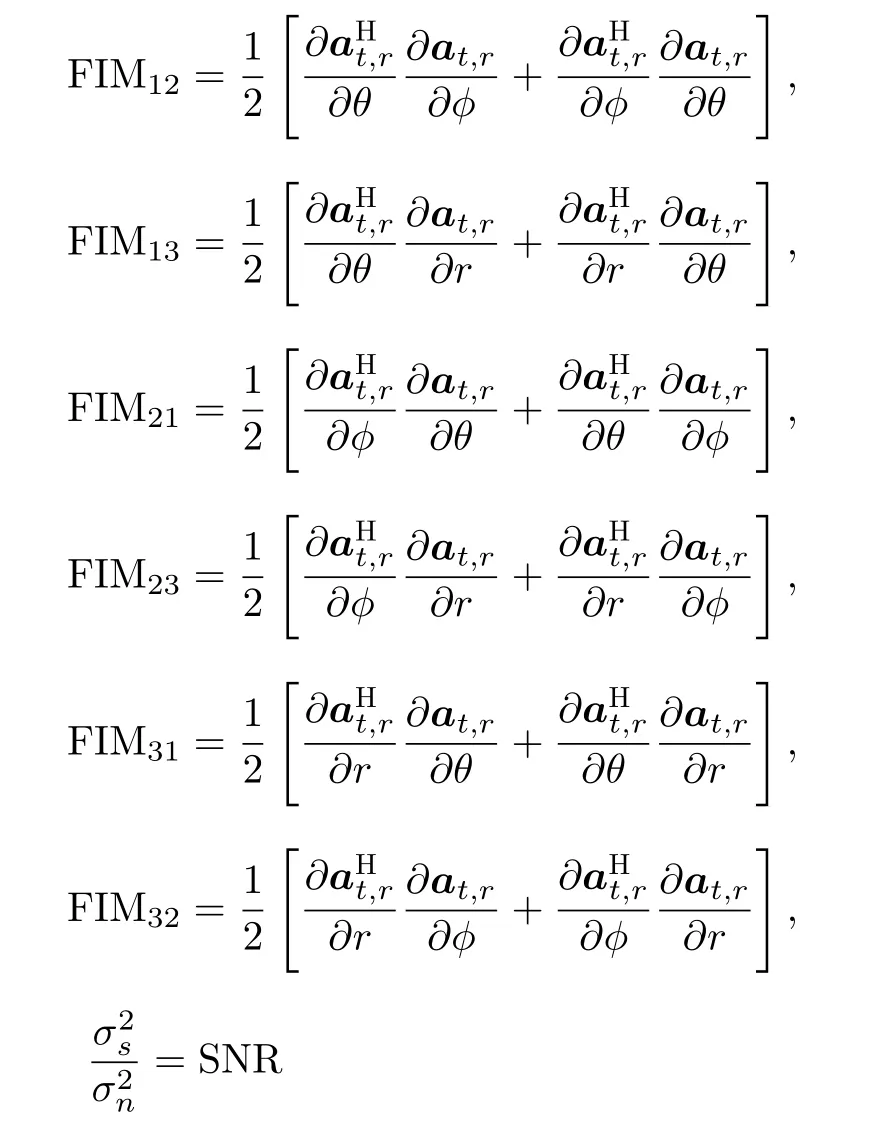
Finally,the CRLB of conformal FDA-MIMO can be calculated by the inverse of Fisher matrix.

3 Reduced-Dimension Target Parameter Estimation Algorithm

The covariance matrix of the conformal FDA-MIMO receiving signal can be written as

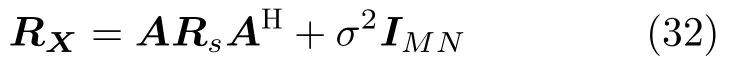
whereRsrepresents the covariance matrix of transmitting signal,IMNdenotesMNdimensional identity matrix.For independent target signal and noise,RXcan be decomposed as

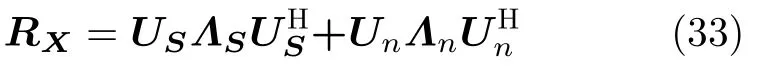
The traditional MUSIC algorithm is utilized to estimate the three-dimensional parameters{θ,φ,r},MUSIC spectrum can be expressed as

The target location can be obtained by mapping the peak indexes of MUSIC spectrum.

Traditional MUSIC parameter estimation algorithm is realized by 3D parameter search,which has good performance at the cost of high computational complexity.When the angular scan interval is less than 0.1°,the running time of single Monte-Carlo simulation is in hours,which is unpracticable for us to analysis conformal FDA-MIMO estimation performance by hundreds of simulations.

In order to reduce the computation complexity of the parameter estimation algorithm for conformal FDA-MIMO,we propose a RD-MUSIC algorithm,which has a significant increase in computing speed at the cost of little estimation performance loss.

At first,we define

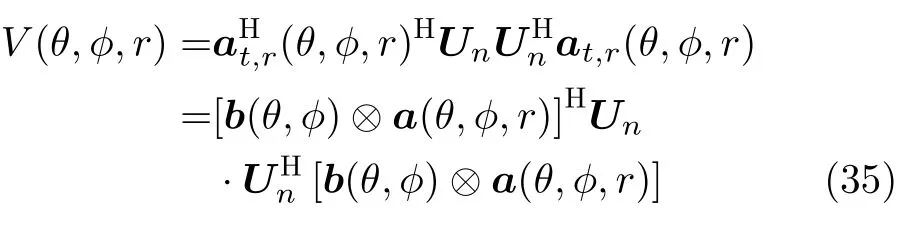
Eq.(35) can be further calculated by

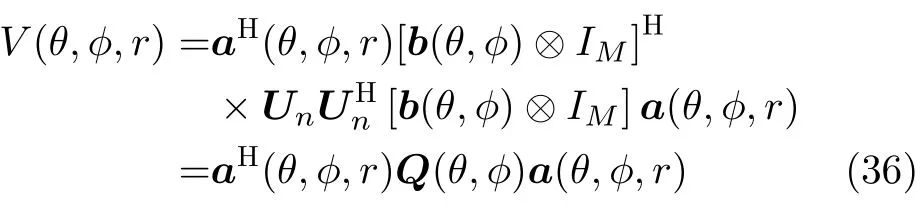
whereQ(θ,φ)[b(θ,φ)⊗IM]HUn[b(θ,φ)⊗IM],Eq.(36) can be transformed into a quadratic programming problem.To avoida(θ,φ,r)0M,we add a constrainta(θ,φ,r)1,wheree1denotes unit vector.As a result,the quadratic programming problem can be redefined as

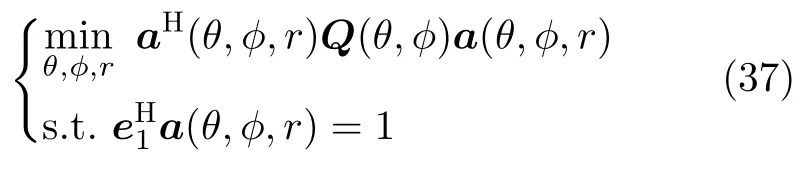
The penalty function can be constructed as

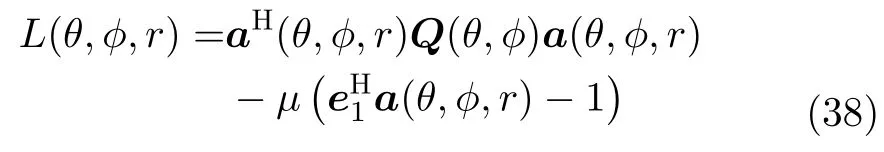
whereµis a constant,becausea(θ,φ,r)a(θ,φ)⊙a(r),so we can obtain

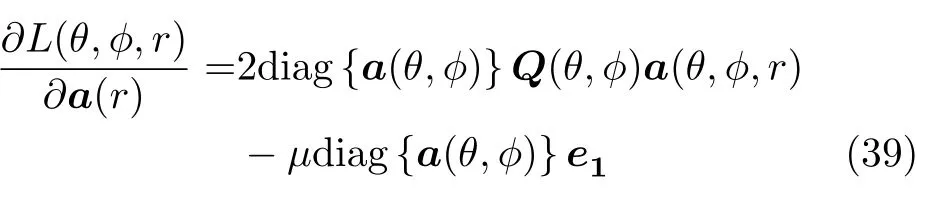
where diag(·) denotes diagonalization.

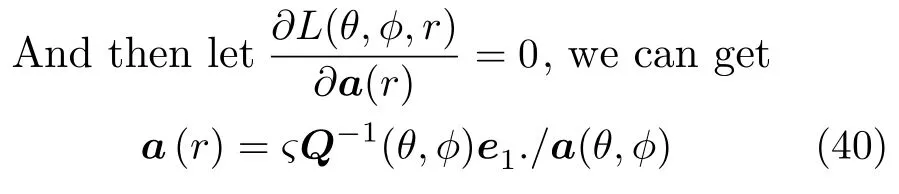
whereςis a constant,./ denotes the division of the corresponding elements,which is opposite of Hadamard product.Substituting the constraint1 intoa(r),we can obtainς·(θ,φ)e1),thena(r) can be expressed as

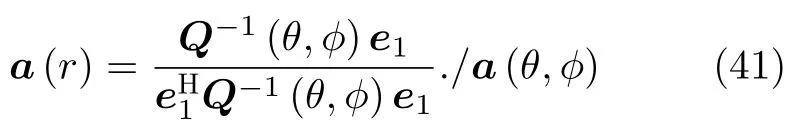
Substitutinga(r) into Eq.(37),the target azimuths and elevations can be estimated by searching two-dimensional azimuth-elevation spectrum,

Given azimuth-elevation estimations obtained by mapping theLpeak points,the range information can be obtained by searching range-dimensional spectrum,

4 Simulation Results

For conformal array,different array layouts produce different element patterns.We select the semi conical conformal array which is shown in Fig.2 as the receiving array for the following simulation.

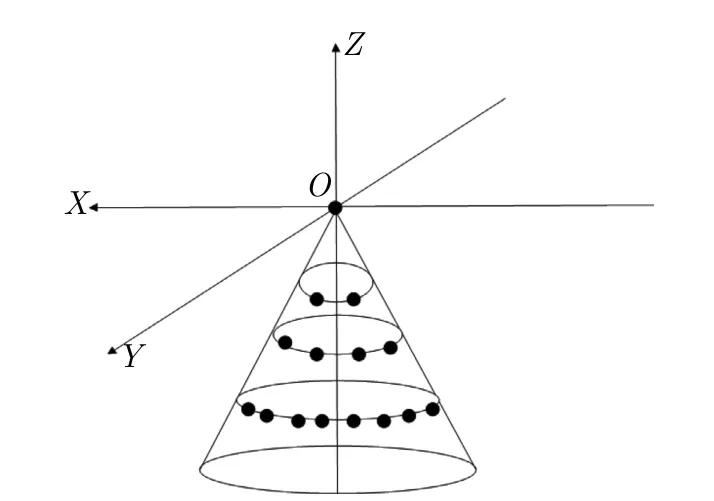
Fig.2 Conformal FDA-MIMO semi conical receiving array

The simulation parameters are provided as follows:M10,N7,f110 GHz,Δf3 kHz,dλ/2c/2f1andc3×108m/s .

4.1 Analysis of computational complexity

We first analyze the computational complexity of the algorithms in respect of the calculation of covariance matrix,the eigenvalue decomposition of the matrix and the spectral search.The main complexity of the MUISC algorithm and our proposed RD-MUISC algorithm are respectively as

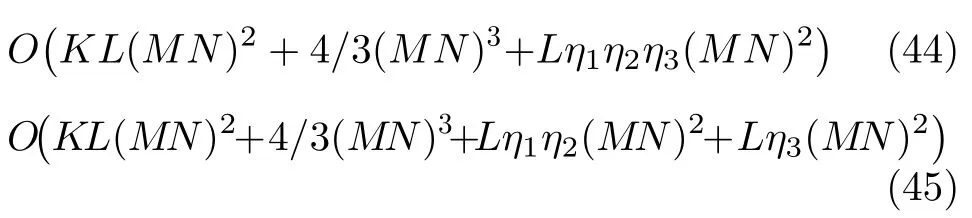
WhereKandLdenote snapshot number and signal sources number,η1,η2andη3represent search number in three-dimensional parameterθ,φ,r,respectively.

From Eq.(44) and Eq.(45),we can see that the main complexity reduction of the RD-MUSIC algorithm lies in the calculation of the spectral search function.With the increase of the search accuracy,the complexity reduction is more significant.

The computational complexity of algorithms is compared in Fig.3.It can be seen from Fig.3 that the difference of computational complexity between the two algorithms gradually increases with the increase of search accuracy.In the case of high accuracy,the computational efficiency of RD-MUSIC algorithm can reach more than 103times of the traditional MUSIC algorithm.The simulation results show that RD-MUSIC algorithm has advantage in computing efficiency for conformal FDA-MIMO.

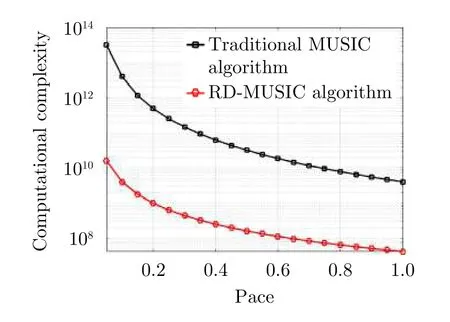
Fig.3 Comparison of computational complexity under different scan spacing

4.2 Single target parameter estimation

In order to illustrate the effectiveness of the RD-MUSIC algorithm for a single target which is located at (30°,20°,10 km),we first give the parameter estimation probability of success with 1000 times Monte Carlo simulation,as shown in Fig.4,the criterion of successful estimation is defined as the absolute difference between the estimation value and the actual value is less than a designed thresholdΓ.More specifically,the criterion is,and supposeΓθΓ ×1°,ΓφΓ ×1°,ΓrΓ ×100 m,i n t h e simulation,as well as the search paces are set as[0.05°,0.05°,0.05 km],respectively.From Fig.4,we can see that the probability of success gets higher asΓgets bigger,which is consistent with expected.

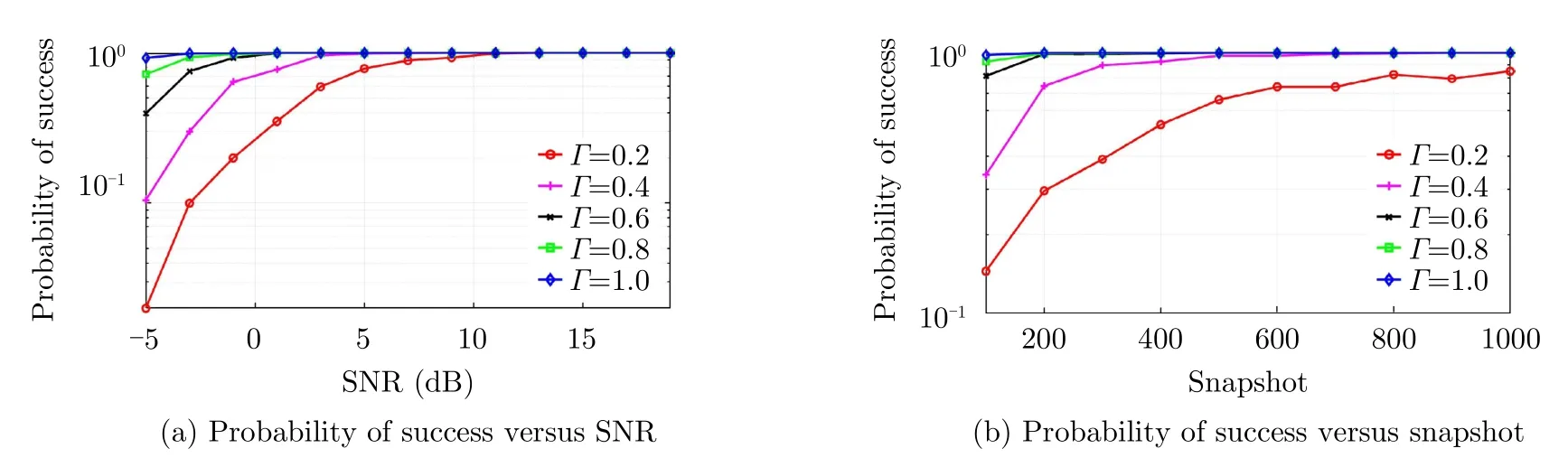
Fig.4 The parameter estimation probability of RD-MUSIC algorithm with different thresholds

Then,we consider the single target parameter estimation performance,Fig.5 shows the RMSE of different algorithms with the increase of SNR under 200 snapshots condition,and Fig.6 demonstrates the RMSE of different algorithms with the increase of snapshot number when SNR0 dB.As shown in Fig.5 and Fig.6,the RMSEs of conformal FDA-MIMO gradually descend with the increasing of SNRs and snapshots,respectively.At the same time,the performance of traditional algorithm is slightly higher than RD-MUSIC algorithm.When the number of snapshots is more than 200,the difference of RMSEs is less than 10−1.Therefore,the performance loss of RD-MUSIC algorithm is acceptable compared with the improved computational speed.Note that,here we set 100 times Monte Carlo simulation to avoid running too long.

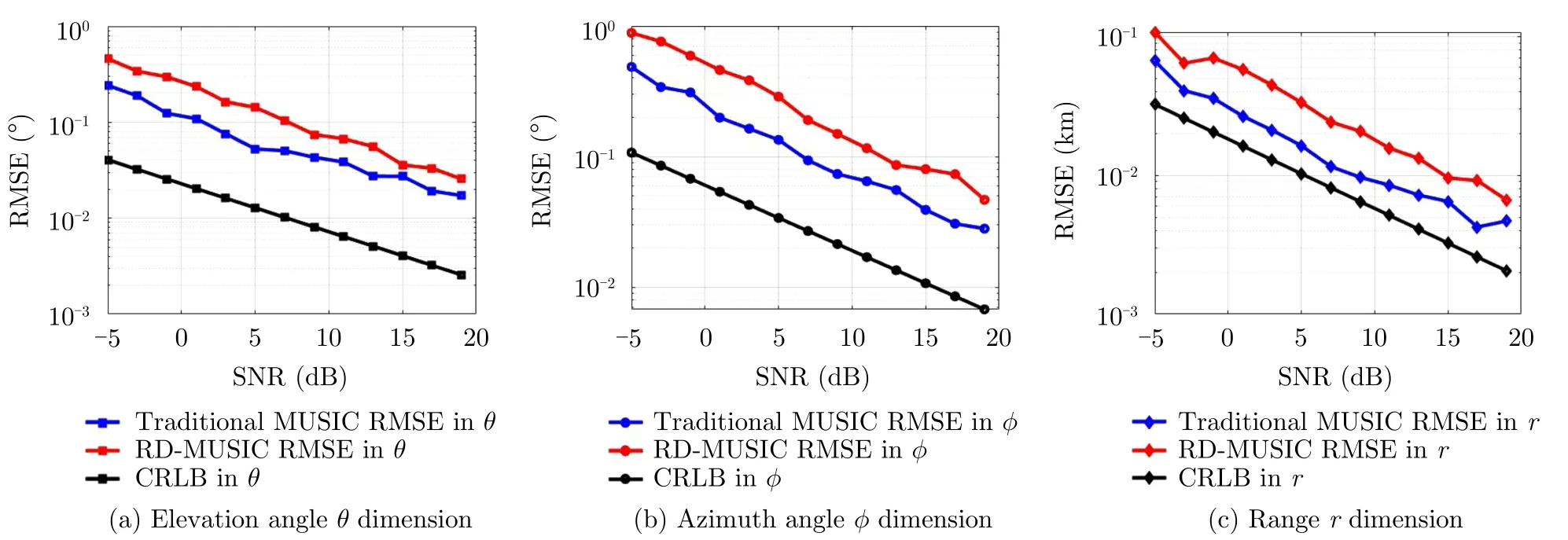
Fig.5 The RMSE versus snapshot for single target case

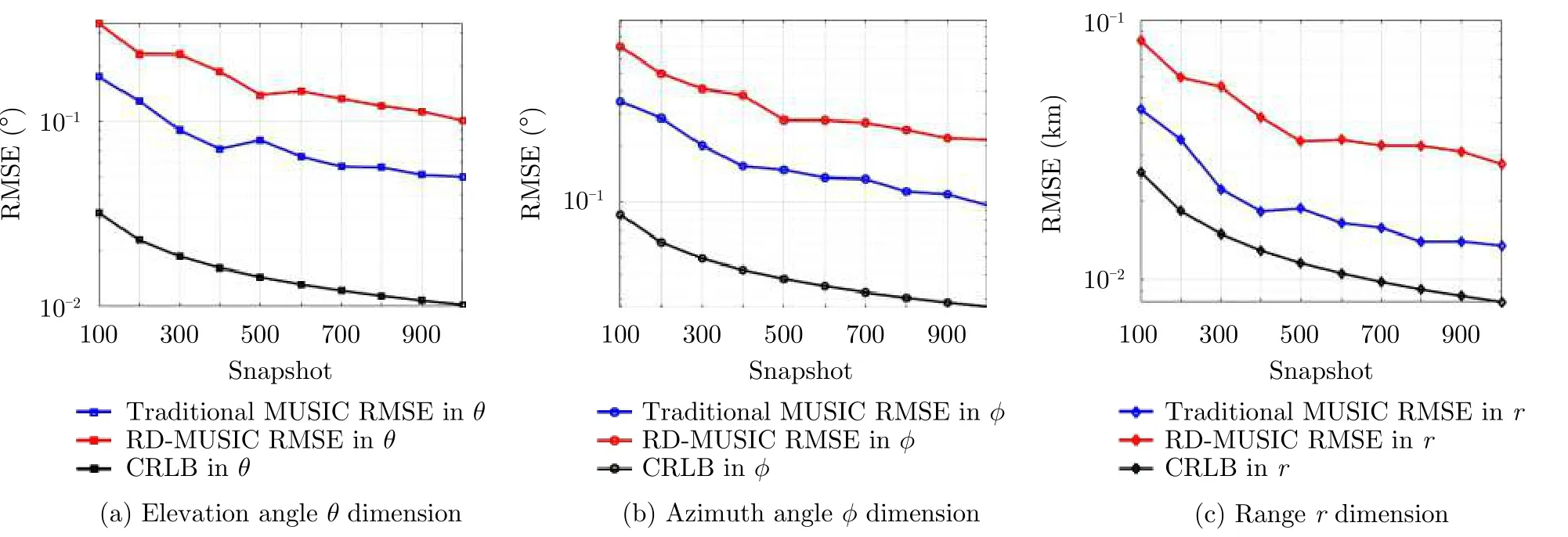
Fig.6 The RMSE versus SNR for two targets case

4.3 Multiple targets parameter estimation

Without loss of generality,we finally consider two targets which are located at (30°,20°,10 km) and (30°,20°,12 km),respectively,the remaining parameters are the same as single target case.Fig.7 and Fig.8 respectively show the RMSE of different algorithms with the increase of SNR and snapshot number in the case of two targets.

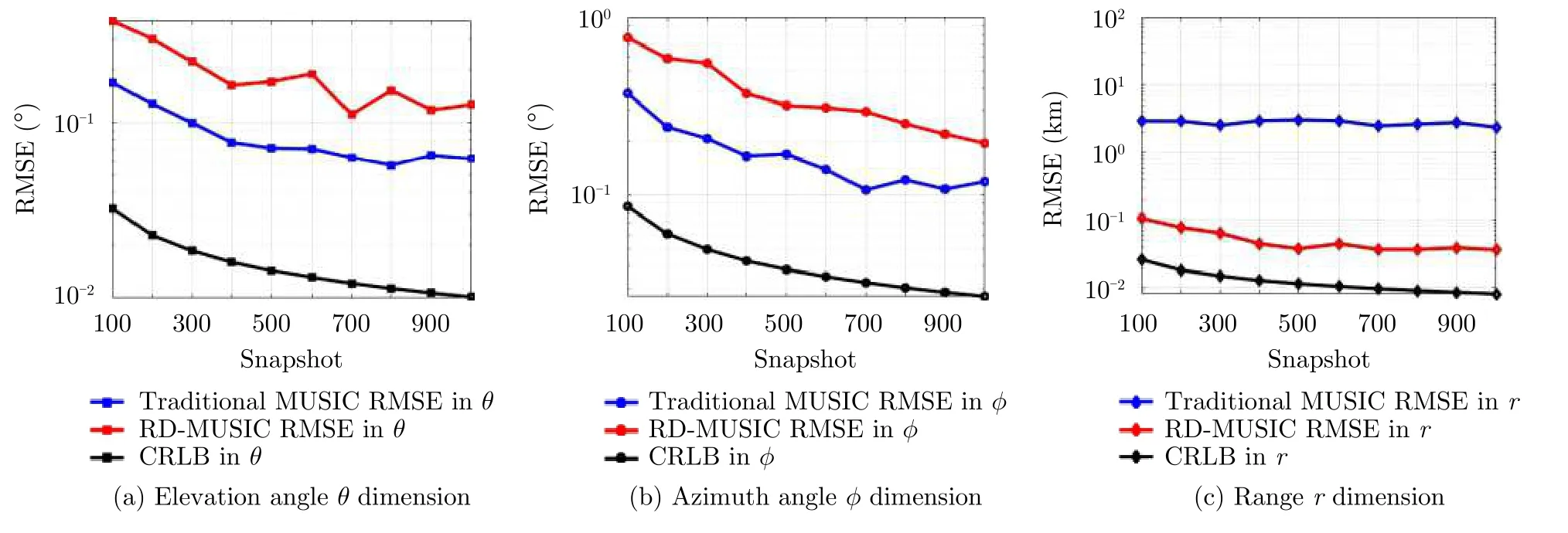
Fig.8 The RMSE versus snapshot for two targets case

It can be seen from Fig.7 that the RMSE curve trend of angle estimation is consistent with that of single target case.The performance of traditional MUSIC algorithm is slightly better than that of RD-MUSIC algorithm.In the range dimension,the performance of traditional algorithm hardly changes with SNR,and RD-MUSIC algorithm is obviously better than traditional MUSIC algorithm.The proposed RD-MUSIC algorithm first estimates the angles,and then estimates the multiple peaks from range-dimensional spectrum,which avoids the ambiguity in the three-dimensional spectral search.Therefore,the RD-MUSIC algorithm has better range resolution for multiple targets estimation.

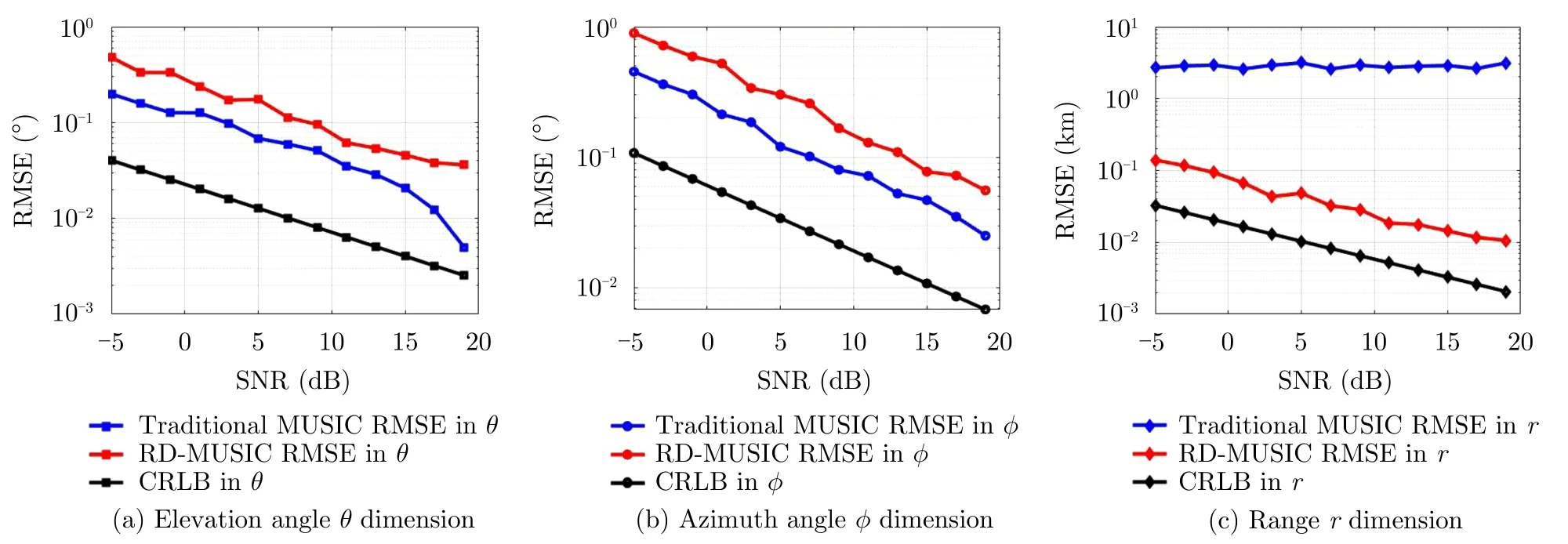
Fig.7 The RMSE versus snapshot for two targets case

5 Conclusion

In this paper,a conformal FDA-MIMO radar is first established,and the corresponding signal receiving mathematical model is formulated.In order to avoid the computational complexity caused by three-dimensional parameter search of MUSIC algorithm,we propose a RD-MUSIC algorithm by solving a quadratic programming problem.Simulation results show that the RDMUSIC algorithm has comparative angle estimation performance with that of traditional MUSIC algorithm while greatly reducing the computation time.And the RD-MUSIC algorithm has better range estimation performance for multiple targets.