圆钢管T型相贯节点面外弯曲刚度及等效支管长度研究
2022-01-07尚仁杰侯兆新
尚仁杰 侯兆新
(中冶建筑研究总院有限公司,北京 100088)
0 引言
相贯节点是钢管结构受力的关键,相贯节点的主管相通、支管端部直接焊接到主管外表面,焊缝可以达到与支管截面等强。但是,由于主管内为空心,无法保证主管截面的平截面假定,主管圆截面在支管作用下由于局部变形而发生畸变,局部变形使得节点不能达到刚接。可以将节点的不完全刚接想象为支管和主管在节点处有一个弹簧连接,本文就是研究这个弹簧的刚度。
近年来,钢管结构被广泛应用在各类建筑中,相贯节点受力性能研究已成为钢结构领域的热点[1-2]。相贯节点研究主要集中于节点变形性能、滞回性能、疲劳性能、抗断裂性能等精细化研究,节点平面外刚度研究属于节点变形性能,多集中在定性考虑是否把支管弯矩传递给主管、节点是刚接还是半刚接,这些研究对于节点内力已知的情况下进行节点验算是必不可少的。但是,要进行钢管结构内力精确分析,需要明确节点刚度的数值,节点刚度是进行精细化内力分析的前提。
《钢结构设计标准》(GB 50017—2017)[3]和《钢管结构技术规程》(CECS 280:2010)[4]给出了相贯节点平面外受弯承载力计算公式。虽然国内进行了大量的相贯节点刚度研究,国外也有面外弯曲刚度计算公式[5],但是,我国规范还没有给出相贯节点平面外局部刚度如何取值,目前的设计软件中也没有考虑节点刚度的输入和计算。
文献[6]把空间网格结构的节点刚度研究分为半刚性节点刚度的数学模型、节点刚度的确定、半刚性节点杆件单元力学模型以及空间结构节点刚度的分类准则等四方面。本文在总结分析现有T 型相贯节点试验研究[7-13]和非线性有限元研究[14~17]成果基础上,用壳单元模拟节点局部变形影响,用管单元考虑节点完全刚接,两者相结合得到节点面外弯曲弹性刚度。给出了等效支管长度,用于直观考虑节点刚度的影响。分析了主管壁厚、支管壁厚、支管直径对节点面外弯曲刚度和等效支管长度的影响。本文的研究属于半刚性节点研究中的平面外弯曲刚度值确定,等效支管长度是一种直观的半刚性单元力学模型。
1 相贯节点面外刚度分析方法
1.1 节点研究基础
同济大学通过试验研究了相贯节点平面外受弯性能[7~9],试验表明,相贯节点支管平面外受弯时具有较高的延性,节点达到极限承载力时的局部转角φu与节点达到屈服承载力时的转角φy[10]达到4,节点承载力低于支管承载力,受荷初始阶段表现为线弹性,初始刚度基本不变[7]。浙江工业大学[11]进行了支主管平面内夹角不同的平面外弯曲研究,试验表明,相贯节点表现出较好的平面外抗震性能和变形能力,节点达到屈服前具有很好的线弹性。浙江大学[12]进行了相贯节点试验,研究了主管应力对节点刚度的影响,试验表明,在应力达到屈曲应力前,荷载—位移曲线为线性变化。长江大学工程技术学院[13]对T 型相贯节点进行低周反复静力加载试验,试验表明支管达到设计强度值时,荷载-位移曲线基本为线性变化。
太原理工大学[14]利用非线性有限元分析研究了T 型相贯节点应力集中和破坏模式,通过变形曲线可以看出,在节点达到极限荷载前的80%均处于线弹性阶段,也就是在设计荷载下可以按线弹性考虑。贵州大学[15]专门研究了节点弯曲刚度,得到在节点支管应力达到屈服应力前,节点弯曲刚度为定值,考虑材料塑性发展,采用非线性有限元对主管240×8 和八个规格壁厚支管80×(4~8)的T型节点支管承载力分析,得到在节点达到《钢结构设计标准》规定的承载力之前,节点荷载-位移基本处于线性阶段。天津大学[16]基于微观断裂机制研究了相贯节点承载力,主管采用406.4×16和324×12.5,支管采用168.3×10,荷载-位移曲线显示,支管应力达到200 MPa 前,节点基本处于线弹性阶段。上海交通大学[17]用非线性有限元研究了相贯节点平面外弯曲过程,分析了初始弹性刚度随管径、厚度的变化规律。
现有的T 型节点试验研究[7-13]和非线性有限元分析[14-17]表明,对于满足规范要求的、常规尺寸的圆钢管T 型相贯节点,平面外弯曲表现出很好的塑性发展,荷载-位移曲线初始有较长段的线性变化,节点弯曲刚度保持为恒定值,在进行结构整体内力分析时可以采用初始弯曲刚度。因此,可以用有限元进行线弹性分析确定节点平面外弯曲刚度。
1.2 节点面外弯曲刚度的分析方法
从相贯节点中心0 到主管的两个端点1、2 和支管的端点3均为2 000 mm长,当杆件足够长时,计算可以反映出三段杆件的弯曲影响(图1)。
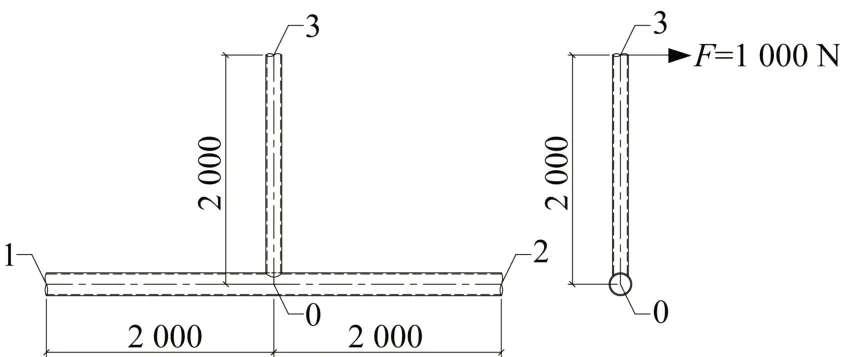
图1 计算模型尺寸(单位:mm)Fig.1 Size of analysis model(Unit:mm)
采用Ansys 有限元软件进行计算分析,钢管材料弹性模量取Es=2.05×105MPa,泊松比μ=0.3。用壳单元Shell63 考虑圆管在节点的局部变形引起的转角影响(图2),用管单元(梁单元)pipe16 不考虑节点局部变形。计算模型中端点1和2采用固定约束,主管0-1、0-2和支管0-3形成一个平面,在端点3施加平面外水平力F=1 000 N,该力垂直于主管和支管形成的平面(图1),用两种模型分别计算端点3平面外水平位移(图3)。
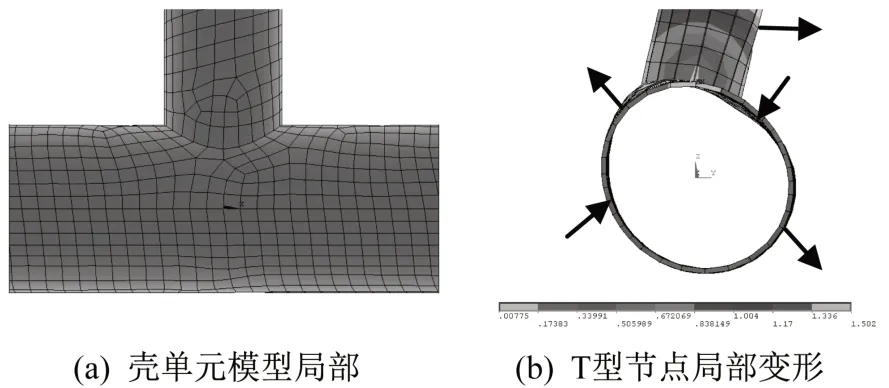
图2 壳单元模型及节点局部变形Fig.2 T-joint local elements of shell model and deformation
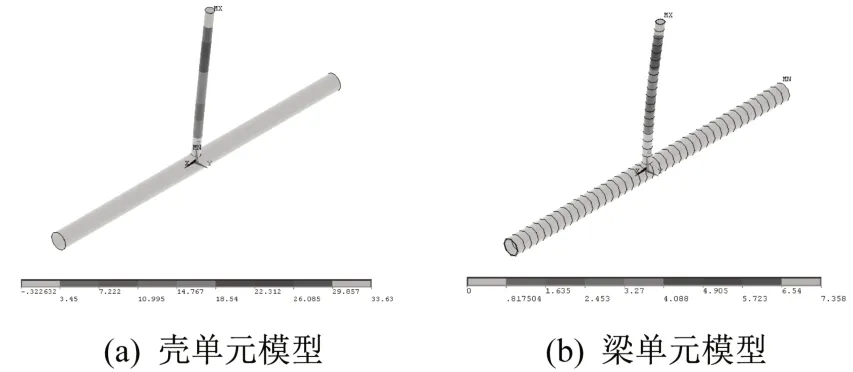
图3 有限元分析位移图Fig.3 Displacement diagrams of finite element analysis
用Shell63 模型计算得端点3 水平位移Δso,图2显示了T型节点单元划分和局部变形,箭头方向表示节点位移方向。可以看出,主管圆截面发生畸变,左上方节点向左上方向变形,右上方节点向左下方向变形,这种变形增大了支管平面外变形,形成了节点的局部平面外转角θo,使得节点不能达到完全刚接。主管的加劲可以明显改善局部变形[18],但是,由于加劲焊接工艺复杂,增加很多的主管端口,一般不采用。
三段杆件用pipe16 单元模拟,计算得端点3平面外水平位移Δpo。
Δso与Δpo两者之差即为节点平面外弯矩产生的局部变形引起的端点3平面外水平位移ΔMo:

节点局部变形引起的支管平面外转角为

水平力F在0点产生的弯矩为

得到节点局部变形的面外弯曲刚度为
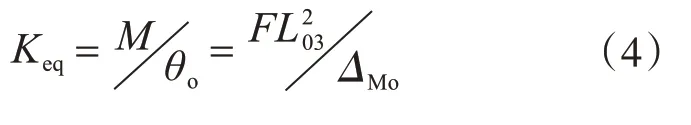
1.3 节点面外弯曲等效支管长度
目前的设计软件没有考虑圆管相贯节点面外弯曲刚度的影响,但是,节点面外弯曲刚度对于结构精细化整体计算是一个必不可少的参数。为了更直观理解相贯节点面外弯曲刚度,本文提出等效支管长度的概念,用支管的等效长度来反映节点局部变形引起的弯曲刚度,直观反映节点面外弯曲刚度的影响。
支管外径为Di,厚度为ti,则支管截面惯性矩为IB=纯弯作用下,等效支管长度Leq对应的弯曲刚度为
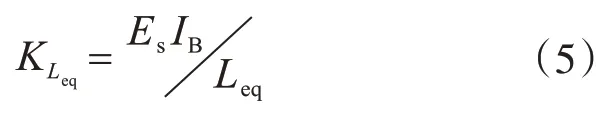
式中,Es为钢材弹性模量。
假设支管长度Leq的弯曲刚度KLeq与节点局部变形弯曲刚度Keq相同,可以得到:

得到等效支管长度为

2 T型相贯节点面外刚度分析
2.1 支管厚度的影响
主管选取外径D=212 mm,壁厚t=12 mm,支管壁中心直径D0i=100 mm,壁厚3~11 mm 变化,支管外径为Di=D0i+ti。采用壳单元Shell63考虑节点局部变形得到Δso,采用梁元(管单元)pipe16,节点按刚接,不考虑节点局部变形,得到Δpo,按式(1)—式(7)得到每种情况下节点面外弯曲刚度和等效支管长度,计算分析结果见表1。
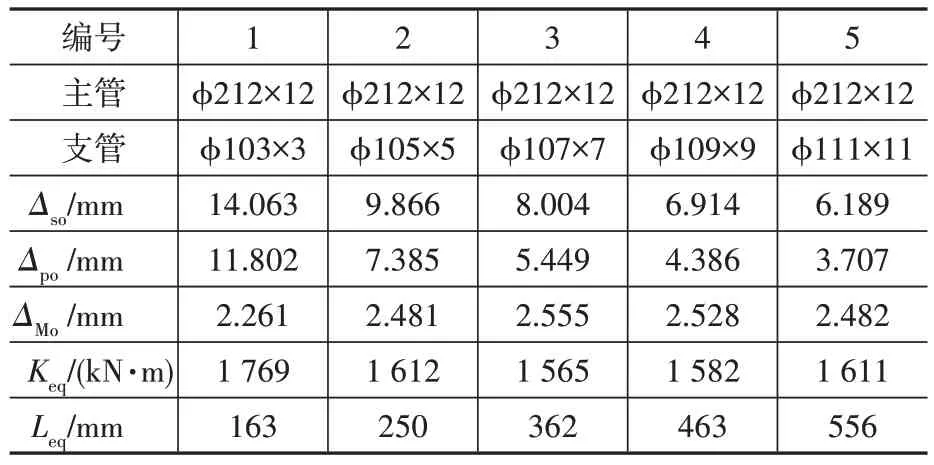
表1 支管变厚度计算结果Table 1 Calculation results of different thickness branch tubes
根据表1 计算的等效节点刚度Keq和支管壁厚数据,绘制出图4;根据等效支管长度和支管壁厚数据,绘制图5。
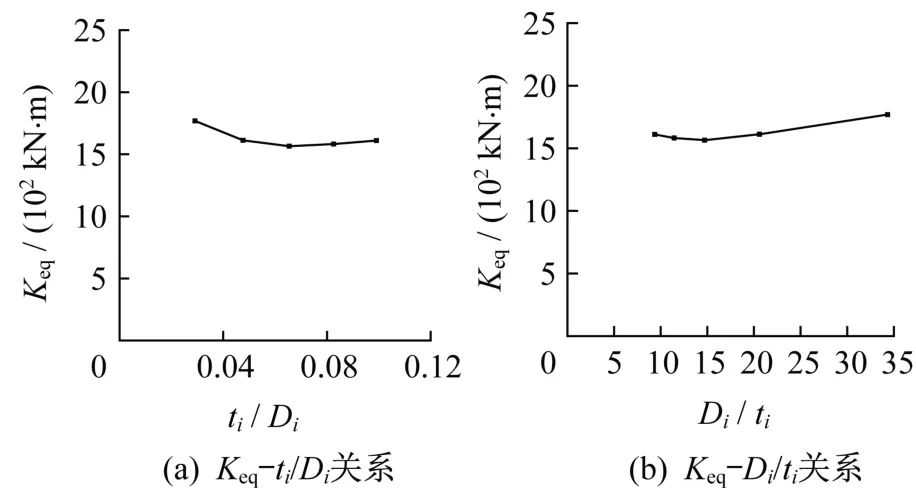
图4 面外弯曲刚度与支管壁厚关系Fig.4 Relationship between out-plane bending stiffness and branch tube thickness
从图4(a)可以看出,支管厚/径比(ti/Di)在0.065 附近时,节点面外弯曲刚度存在极小值;支管厚/径比在0.065 附近时,在主管不变,支管直径确定时,支管壁厚对节点面外弯曲刚度影响较小。从图4(b)可以看出,支管径/厚比(Di/ti)在常用范围15~35 时,刚度随支管径/厚比基本成线性增加,但是增加仅仅12%,增加量相对较小;支管径/厚比在15 左右时刚度存在最小值,最大值和最小值之比仅仅为1.13,相差不大。
从图5(a)可以看出,节点平面外弯曲刚度的等效支管长度与支管厚/径比(ti/Di)基本成线性关系;支管厚/径比为0.03 时,节点平面外弯曲刚度的等效支管长度为163 mm,约为1.5 倍支管直径;随着支管的壁厚增加,节点等效支管长度越来越大,支管厚/径比为0.1 时,等效支管长度为556 mm,约为5 倍支管直径,刚度影响不可忽视;当支管厚/径比趋于0 时,等效支管长度有趋于0的趋势。从图5(b)可以看出,等效支管长度随支管径/厚比(Di/ti)的增大而减小。等效支管长度用图5(a)支管厚/径比(ti/Di)作为自变量表示,具有明显的线性性,比图5(b)用支管径厚比(Di/ti)作为自变量表示更为直观。
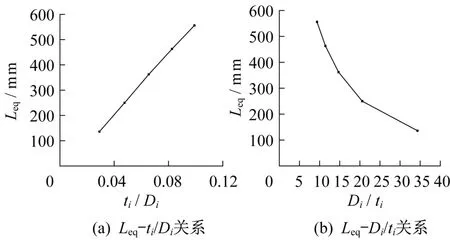
图5 等效支管长度与支管壁厚(径厚比)关系Fig.5 Relationship between equivalent branch tube length and branch tube thickness
2.2 支管直径变化的影响
主管选取外径D=212 mm,壁厚t=12 mm,保持不变;支管壁厚取7 mm不变,支管外径Di=107~187 mm 变化。与2.1 节一样,采用壳单元shell63考虑节点局部变形得到Δso,采用梁元(管单元)pipe16 不考虑节点局部变形,得到Δpo,按式(1)—式(7)得到每种情况的节点面外弯曲刚度和等效支管长度,计算分析主要结果见表2。
根据表2 计算的等效节点刚度Keq和支/主管外径比(Di/D),绘制出图6;根据等效支管长度和支/主管外径比(Di/D),绘制图7。
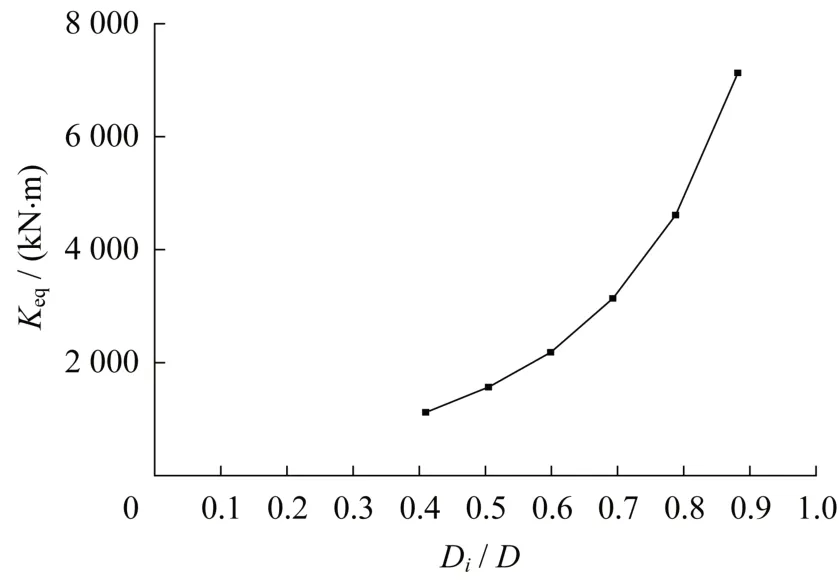
图6 面外弯曲刚度与支/主管外径比的关系Fig.6 Relationship between out-plane bending stiffness and branch tube diameter
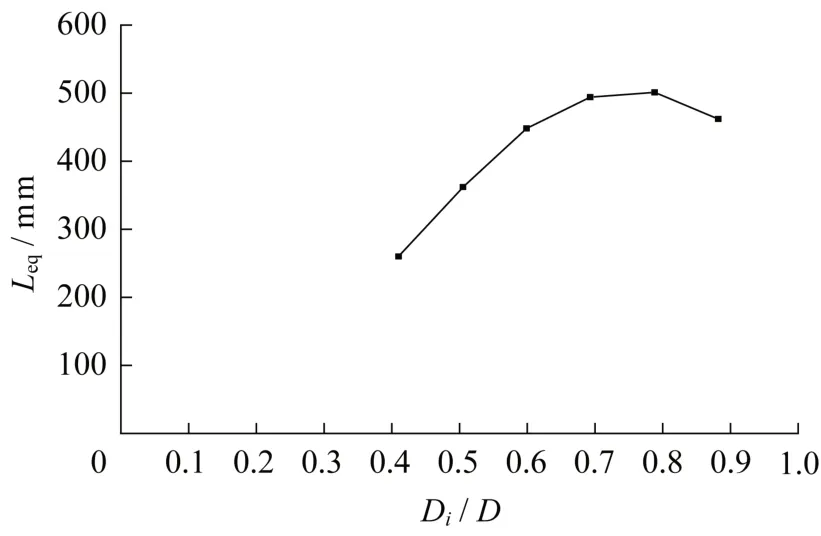
图7 等效支管长度与支/主管外径比的关系Fig.7 Relationship between equivalent branch tube length and branch tube diameter
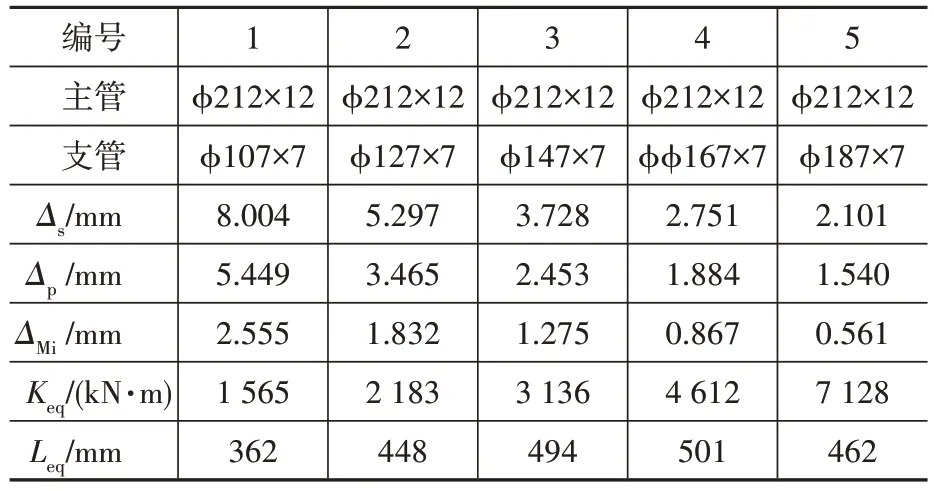
表2 不同直径支管计算结果Table 2 Calculation results of different diameter branch tubes
从图6 可以看出,当支/主管外径比较小时,节点刚度较小;当支/主管外径比趋于0 时,节点面外弯曲刚度有趋于0 的趋势;随着支/主管外径比增加,节点平面外弯曲刚度逐渐增大,曲线斜率越来越大,刚度增长速度增大。
从图7 可以看出,当支/主管外径比为0.5 时,节点等效支管长度为326 mm;随着支/主管外径比增大,等效支管长度在增大;当支/主管外径比为0.75 左右时,等效支管长度存在极大值,约为510 mm;当支/主管外径比继续增大时,等效支管长度开始下降;支/主管外径比趋于0 时,等效支管长度也有趋于0的趋势。
2.3 主管厚度的影响
选取常用钢管规格进行分析,为了便于建模分析,取主管壁中心直径D0=200 mm,壁厚t=5~14 mm,主管外径D=D0+t;支管外径Di=105 mm,支管壁厚ti=5 mm保持不变。主要计算分析结果见表3。
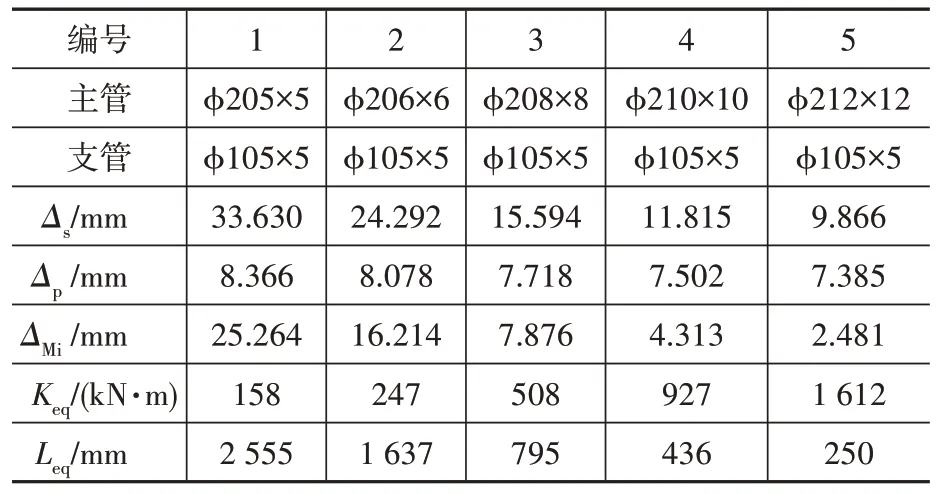
表3 不同主管厚度计算结果Table 3 Calculation results of different thickness main tubes
根据表3 节点面外弯曲刚度Keq和主管壁厚绘制图8;根据等效支管长度和主管壁厚绘制图9。
从图8(a)可以看出,随着主管厚/径比增加,节点平面外弯曲刚度在逐渐增加,且增加呈非线性,曲线斜率越来越大,刚度增长速度增加;当主管厚/径比减小并理论上趋于0 时,节点平面外弯曲刚度有趋于0 的趋势。图8(b)可以看出,节点平面外弯曲刚度随主管径/厚比增大而减小。
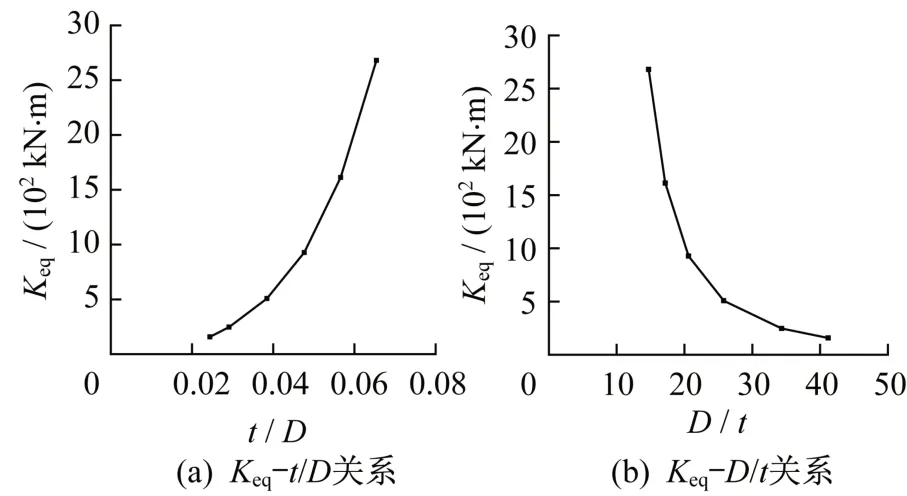
图8 面外弯曲刚度与主管壁厚关系Fig.8 Relationship between out-plane bending stiffness and main tube thickness
从图9(a)可以看出,主管厚/径比为0.025时,节点平面外弯曲刚度与长度为2 555 mm 的支管弯曲刚度等效,对于支管总长为2 000 mm 左右的钢结构节点,等效长度超过构件长度,该弯曲刚度将严重影响结构的整体刚度,进而影响结构变形和结构内力重分布;随着主管的壁厚增加,节点等效支管长度逐渐减小,当主管厚/径比为0.055 时,等效支管长度为250 mm,当主管厚/径比继续增大时,节点等效支管长度有趋于0 的趋势。图9(b)用主管径/厚比作自变量表达更为直观,主管径/厚比为15时,节点等效支管长度仅仅150 mm,基本可以忽略不计;当主管径/厚比为35 时,节点等效支管长度达到1 600 mm 以上,会严重影响结构内力。
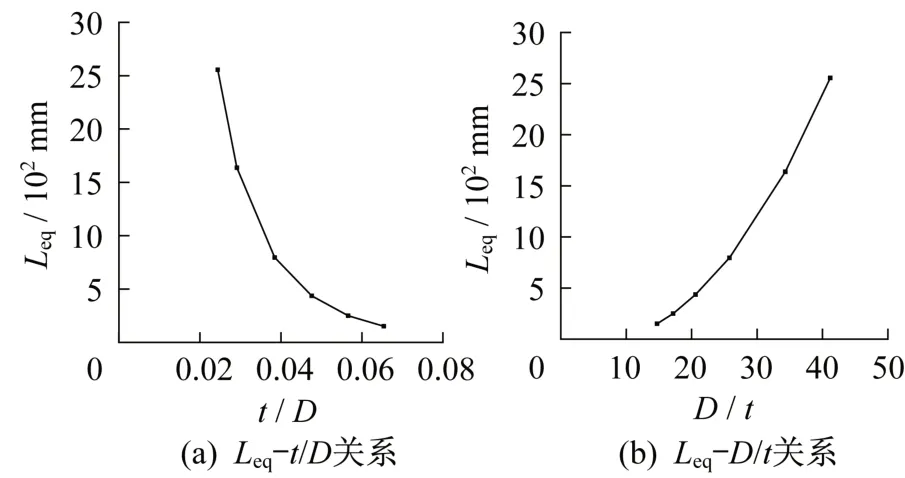
图9 节点等效支管长度与主管壁厚关系Fig.9 Relationship between equivalent branch tube length and main tube thickness
从图9 可以总结出:对于承受面外弯矩的T型相贯节点,主管壁厚不宜太小,主管210×10对应的面外弯曲等效支管长度达到436 mm,已经为4 倍支管外径和2 倍主管外径,主管作为T 型节点支管的支座,且支管主要承受平面外弯曲时,D/t不宜大于20。
从图4、图6、图8 可以看出,本文给出了面外弯曲刚度的数值大小,便于计算分析,可以用于结构分析,输入软件中进行计算。从图5、图7、图9可以看出,用等效支管长度的概念来反映节点平面外弯曲刚度更加直观,便于理解,对于工程设计更为方便。
3 工程算例
北京市温榆河公园1号大门采用了圆钢管焊接而成的单层曲面结构,结构平面布置和立面图见图10和图11。平面长度72.74 m,宽度20.35 m,立面高度9.4 m,两端落地,中间有4根柱子支撑。
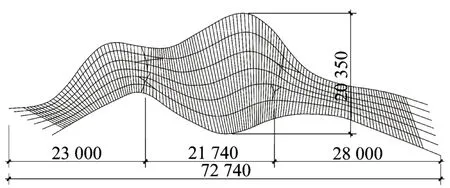
图10 钢管结构屋面平面布置(单位:mm)Fig.10 Plane layout of steel tube structure(Unit:mm)
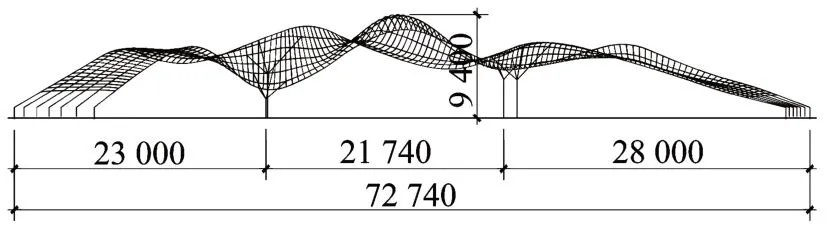
图11 钢管结构屋面立面图(单位:mm)Fig.11 Elevation drawing of steel tube structure(Unit:mm)
平面上有纵向7根主梁组成,两侧2根主梁外径D=325 mm,中间5 根主梁外径D=219 mm,厚度t=12 mm 和16 mm,主梁在与柱子节点处壁厚为20 mm。7 根主梁之间为外径Di=102 mm、120 mm和140 mm 的横向次梁。外侧2 主梁钢管与横向次梁钢管均为T 型相贯节点,中间5 根主梁钢管与次梁钢管之间为X型相贯节点。结构设计中考虑了相贯节点局部变形引起的面外刚度影响,计算结果见表4。屋面中间部分支管长度大都在3 000 mm 左右。对于外侧主梁325×12 和次梁120×10 相贯节点,平面外等效支管长度达到1 169 mm,与构件长度3 000 mm 相比,刚度折减约30%;对于主梁325×16 和次梁140×10 相贯节点,等效支管长度为522 mm,与次梁长度3 000 mm相比,刚度折减约15%。
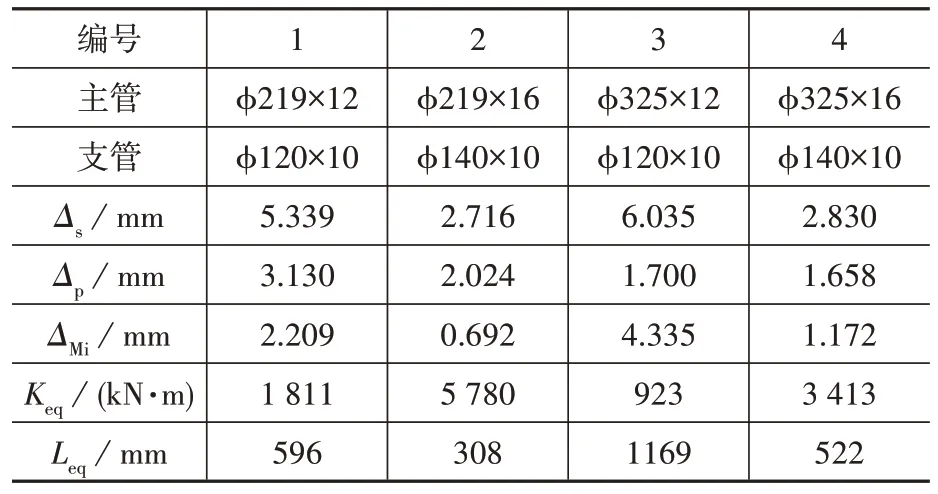
表4 工程实例计算结果Table 4 Calculation results of an engineering example
4 结论
在总结圆钢管相贯节点试验研究和非线性有限元分析基础,利用有限元分析进行了T 型相贯节点面外弯曲刚度分析,并提出了用等效支管长度考虑节点平面外弯曲刚度的方法。通过本文研究,可以得到以下结论:
(1)圆钢管T 型相贯节点试验研究和非线性有限元分析成果表明,结构受力过程中,节点具有很高的塑性发展,达到承载力前,节点转角变形和节点支管弯矩有很长的线弹性阶段,可以利用线弹性初始刚度进行结构整体计算,精细化分析结构内力。
(2)利用壳单元和管单元进行了节点有限元分析,得到了节点局部变形引起的节点面外弯曲刚度计算方法,并提出了面外弯曲等效支管长度概念和计算方法。
(3)得到了节点局部变形引起的节点面外弯曲刚度和等效支管长度与支管厚度、支管直径、主管厚度之间的关系。
