地表变坡下浅埋偏压隧道围岩压力计算方法

杜建明，房倩，海路，麦海颖，王赶

(北京交通大学隧道及地下工程教育部工程研究中心，北京，100044)

近年来，随着我国中西部基础设施建设进程的日益加快，隧道建设取得了巨大成就。中西部地形地势复杂多变，由于地形不对称或地质因素复杂导致隧道结构双侧面荷载不对称而出现偏压隧道。相比于无偏压隧道工程，偏压隧道结构受力更为复杂，施工风险更高，若结构设计或施工方案不合理，则极易发生安全事故，因此，围岩压力的合理确定一直是浅埋偏压隧道工程结构设计和施工方案编制的重点和难点[1]。

研究浅埋偏压隧道围岩压力分布特征的方法主要有现场实测、模型试验、数值模拟和理论计算4 种方法。安鹏程[2]对浙江省诸永高速公路偏压隧道围岩压力分布特征及变化规律进行了现场实测；高杰[3]对鹤大高速公路回头沟偏压隧道围岩压力进行了现场实测，并对围岩应力演化过程及破坏模式进行了研究。现场实测虽然能够获得真实的围岩压力，但实测精度受监测设备及现场环境影响较大，且多针对具体工程进行。在模型试验方面，周晓军等[4]根据相似理论，对地质顺层岩体作用与隧道衬砌结构上的偏压荷载进行了模型试验，对偏压隧道围岩压力分布特点及其与不同顺层倾角之间的关系进行了研究；雷明峰等[5]基于相似物理模型试验对不同倾角下浅埋偏压隧道围岩压力的动态变化规律及分布形式进行了系统研究。模型试验基于相似原理能够较为真实地再现围岩压力分布规律，但隧道开挖技术与支护方式的准确性与相似性有待进一步提高，且相比于数值模拟方法，模型试验的时效性与经济性也不利于工程实际中的推广应用。在数值模拟方面，王磊[6]利用通用有限元计算软件对不同倾角下偏压隧道围岩压力分布特征进行了研究；王传智[7]利用有限差分数值软件对十堰至天水联络线高速公路新安岭隧道不同施工工法下围岩压力的分布特点进行了数值分析。利用计算机程序求解数学模型的近似解，所需时间短，费用低，但模拟结果受力学参数及假设性本构关系影响较大。在理论计算方面，刘翔等[8−9]根据极限平衡法推导出了拱顶地表处于不规则地形条件下浅埋偏压隧道松动围岩压力的计算公式，并成功应用于贵广高速铁路某隧道工程；张治国等[10−14]在考虑地震作用力综合效应的情况下，对地震力偏角进行旋转，然后采用拟静力法提出了黏聚力和内摩擦角分算的浅埋偏压隧道围岩压力解析解。在对现场实际情况进行适当简化的前提下，通过数学建模及力学推导，从而建立围岩压力解析公式。虽然理论计算的解析解与现场实测值之间存在一定误差，但这种误差范围在工程上是可接受的，且其普遍性、时效性与经济性都便于其在工程实际中应用推广。上述研究成果极大地丰富了浅埋偏压隧道围岩压力分布特征及确定方法的相关内容。

然而，当隧道一侧因施工需要开挖路基变坡[15]时，导致岩土体量和坡度均发生变化，此时，需对现有浅埋偏压隧道围岩压力计算公式进行适当修正。基于此，严涛等[16]运用极限平衡原理推导了单次变坡下浅埋偏压隧道围岩压力解析解，变坡面的存在使围岩偏压率增大，结构安全性下降。当隧道一侧坡度较高或较陡时，需要进行2次或多次变坡，从而降低边坡坍塌事故发生的概率。目前，现有文献仅对隧道一侧单次变坡下围岩压力计算公式进行了理论推导，有关2次变坡下浅埋偏压隧道的围岩压力计算公式以及参数影响分析的文献较少。

为此，本文作者采用极限平衡法[17]对2次变坡下浅埋偏压隧道围岩压力的计算方法进行研究，同时分析变坡面坡度变化对围岩压力的影响。

1 围岩压力计算模型及公式推导

JTG D70—2004“公路隧道设计规范”[18]中有关浅埋偏压隧道围岩压力计算公式主要适用于自然放坡下的隧道，即隧道拱顶岩土体坡度保持一致的情况，如图1(a)所示。当需要在隧道开挖路基变坡时，示意图如图1(b)所示。若坡度较高或较陡，则需要进行2次甚至多次变坡，从而防止边坡坍塌事故发生，如图1(c)所示。当隧道一侧施工变坡段以后，围岩压力会因岩土体积、质量和山体坡度变化而发生改变，若继续采用规范公式计算围岩压力，则会产生一定误差。因此，需要对变坡面浅埋偏压隧道围岩压力需要进行修正计算。

图1 坡度变化示意图Fig.1 Schematic diagrams of slope change

1.1 计算模型

1.2 计算公式推导

1.2.1 基本假设

对于2次变坡面浅埋偏压隧道围岩压力计算过程进行如下假设：

1)隧道周围岩土体为均匀连续、各向同性体，且服从摩尔−库仑屈服准则。

2) 隧道拱顶上覆岩土体BCNM下沉过程中，带动隧道两侧块体ABL和CDFK分别沿各自的破裂面AL和FK滑动，与此同时，隧道两侧块体ABL和CDFK对拱顶上覆岩土体BCNM有摩擦阻力作用。

3)破裂面为平面，浅埋情况下破裂面能够发展至地表。

4)隧道深埋侧(内侧)和浅埋侧(外侧)位置的垂直土压力q1和q2间符合线性变化规律，且线性斜率与隧道拱顶地表自然放坡的坡度一致。水平土压力e11与e12以及e21与e22间符合线性变化规律，且底部水平土压力比上部压力大。

5) 假变坡段DEFG始终位于隧道外侧，即变坡段DEFG始终位于CK平面右侧。

1.2.2 块体自重计算公式

设隧道拱顶上覆岩土体(BCNM)自重为W；隧道深埋侧滑动块体ABL自重为W1；隧道浅埋侧所有岩土体(CDEFGHIJK)总自重为W2，其中，滑动块体CDFK自重为W21，滑动破裂面FK下部块体FGK自重为W22，且W21=W2−W22。根据图2(a)所示计算模型可知，隧道开挖轮廓线四周岩土体的自重计算公式分别如下：

图2 围岩压力计算模型与示意图Fig.2 Calculating model and sketch of surrounding rock pressure

式中：γ为岩土体重度。

通过联合求解式(6)与式(7)可得：

1.2.3 块体滑动阻力计算公式

基于极限平衡法原理，取隧道深埋侧块体ABL为研究对象，块体ABL的受力图如图3 所示。其中，Q和q分别为隧道拱顶上方土体的集中荷载与均布荷载；F1为滑动破裂面AL上摩擦阻力与法向作用力的合力，τ11为块体ABL下滑过程中岩土体内部黏聚力引起的抗剪力，τ11=cLAL，c为岩土体内部的黏聚力，LAL为滑动破裂面AL的长度；T1为隧道拱顶上方岩土体(BCNM)右侧面CN上摩擦阻力与法向作用力的合力，τ12为隧道拱顶上方岩土体(BCNM)下沉过程中黏聚力引起的抗剪力，τ12=ch1。为了便于公式推导，将竖直方向合力分解为y11和。

图3 块体ABL的受力图Fig.3 Force diagrams of block ABL

根据块体ABL的受力图，由正弦定理可得：

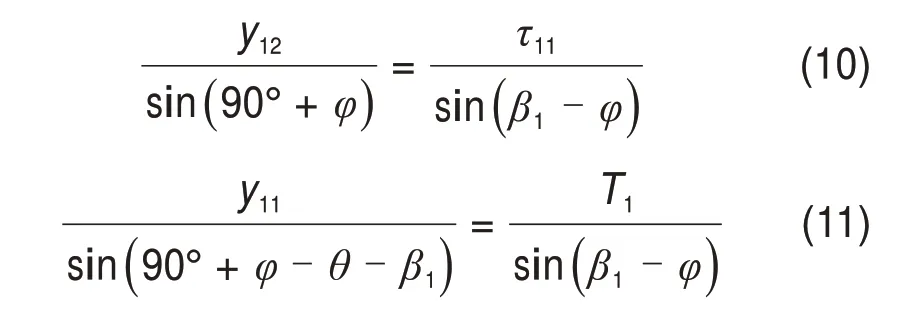
式中：φ为岩土体内部摩擦角；θ为隧道拱顶上方岩土体下沉过程中接触面BL与其之间的摩擦角。

将τ11=cLAL代入式(10)可得

根据极限平衡法原理可得

将式(12)代入式(13)，经整理得

将式(12)、式(14)代入式(11)，经整理得：

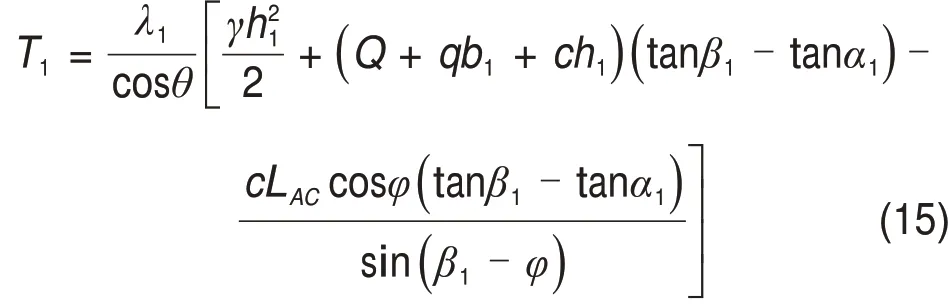
式中：T1为隧道深埋侧块体ABL的滑动阻力；λ1为隧道深埋侧水平侧压力系数。

根据JTG D70—2004“公路隧道设计规范”[18]，隧道深埋侧滑动块体ABL滑动面的破裂角β1可用下式计算：

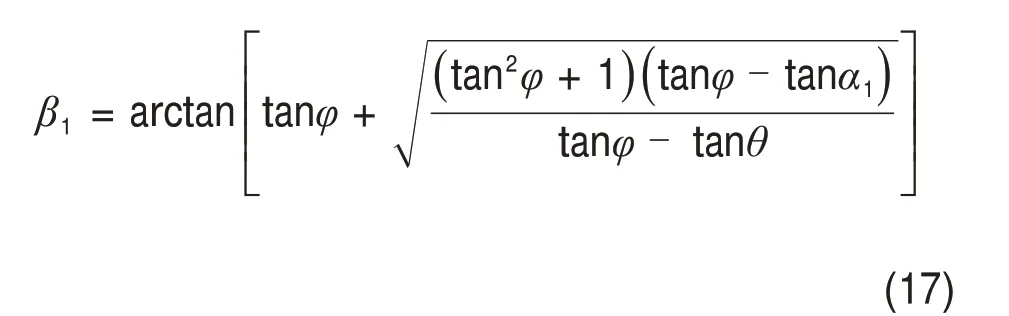
在实际工程中，可以不考虑均布荷载q、集中荷载Q以及黏聚力c，即q=0 kN/m，Q=0 kN/m，c=0 kPa[8]，则式(15)可简化为

将式(17)分别代入式(16)和式(18)即可求得T1与λ1。

同理，基于极限平衡法原理，取隧道浅埋侧块体CDEFK为研究对象，块体CDEFK的受力图如图4 所示。隧道浅埋侧块体CDEFK滑动阻力与深埋侧块体ABL滑动阻力推导过程相类似，在此省略推导过程，直接给出滑动阻力T2的计算公式：

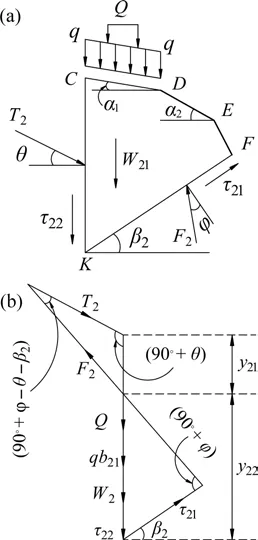
图4 块体CDEFK的受力图Fig.4 Force diagrams of block CDEFK

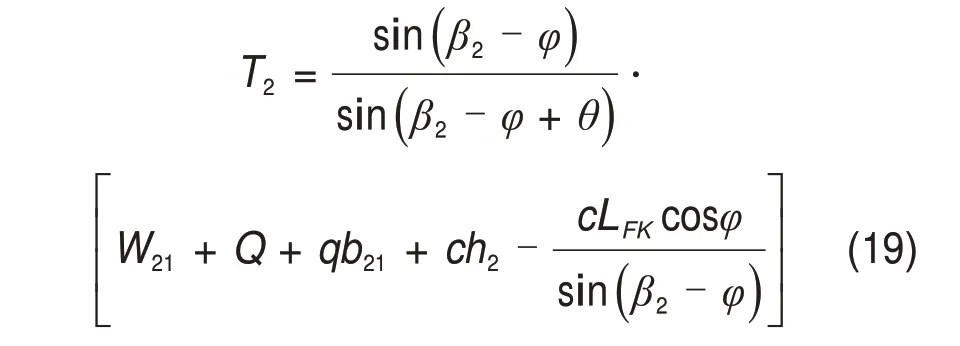
根据土力学理论可得隧道浅埋侧水平侧压力系数λ2的计算公式为

根据JTG D70—2004“公路隧道设计规范”[18]，隧道浅埋侧滑动块体CDEFK滑动面的破裂角β2可用下式计算：

同理，在不考虑均布荷载q、集中荷载Q以及黏聚力c[8]时，式(19)和式(20)可分别简化为：

将式(5)和式(21)分别代入式(22)和式(23)即可求得隧道浅埋侧块体CDEFK滑动阻力T2与水平侧压力系数λ2。

1.2.4 围岩压力计算公式

1)围岩垂直压力。基于极限平衡法原理，以隧道拱顶岩土体BCNM为研究对象，块体BCNM的受力图如图5所示。图5中，T'1和T'2分别为T1和T2的反作用力，τ'12和τ'22分别为τ12和τ22的反作用力。隧道拱顶处围岩垂直压力之和N可用如下公式进行计算：

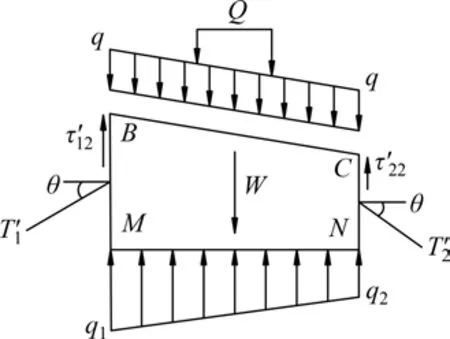
图5 块体BCNM的受力图Fig.5 Force diagram of block BCNM

隧道深埋侧围岩垂直压力q1计算公式如下：

隧道浅埋侧围岩垂直压力q2计算公式如下：

同理，在不考虑均布荷载q、集中荷载Q以及黏聚力c[8]时，式(25)和式(26)可分别简化为：

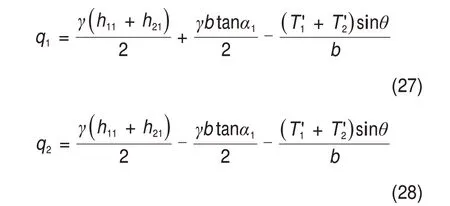
将式(18)和式(22)分别代入式(27)和式(28)即可求得隧道深埋侧和浅埋侧围岩垂直压力q1和q2。

2)围岩水平压力。根据JTG D70—2004“公路隧道设计规范”[18]中围岩水平压力计算公式可求得隧道深埋侧水平围岩压力计算公式如下：

式中：i=1，2。

隧道浅埋侧水平围岩压力计算公式如下：

将式(16)和式(23)代入式(30)即可求得对应的围岩水平压力。

2 与规范公式对比分析

通过采用本文推导的修正公式与规范公式对存在2次变坡下浅埋偏压隧道围岩压力分别进行计算，选取隧道几何参数b1=15 m，b=10 m，b21=5 m，b23=18 m，h1=20 m，h11=8 m，h2=18 m，h21=6 m，h22=16 m，α1=10°，α2=20°，α3=55°；力学参数参考Ⅵ级围岩选取φ=30°，θ=15°，γ=16 kN/m3。计算结果如表1所示。由表1可知：隧道深埋测围岩垂直和水平压力始终比浅埋侧的压力大，表明变坡段并未改变隧道的偏压效应；由于变坡段的存在，隧道浅埋侧的水平围岩压力修正公式计算值比规范公式计算值小，相对误差为38.68%～38.83%，垂直围岩压力修正公式计算值比规范公式计算值大，相对误差为36.40%；隧道深埋侧的垂直围岩压力修正公式计算值比规范公式计算值大，相对误差为19.37%，水平围岩压力保持不变，表明变坡段对隧道浅埋侧围岩压力影响较大。

表1 围岩压力计算结果对比Table 1 Comparisons of calculation results of surrounding rock pressure

将隧道深埋侧围岩压力与浅埋侧围岩压力之比定义为隧道偏压率[20]。采用修正公式与规范公式对隧道偏压率分别进行计算，计算结果如表2 所示。由表2可知：对于围岩垂直偏压率，修正公式计算值比规范公式计算值小，表明变坡段的存在降低了围岩垂直方向的偏压率；对于围岩水平偏压率，修正公式计算值比规范公式计算值大，表明变坡段的存在提高了围岩水平方向的偏压率。相比于规范计算公式，修正计算公式在计算围岩压力时有效考虑了由于变坡段的存在而导致隧道浅埋侧岩土体体积与质量减小，所以，浅埋侧围岩水平压力修正公式计算值比规范公式计算值小；由于隧道浅埋侧滑动阻力T2减小，从而导致围岩垂直压力增大。

表2 隧道偏压率计算结果对比Table 2 Comparisons of calculation results of ratio of unsymmetrical pressure for tunnel

3 变坡段坡度变化影响分析

在不考虑均布荷载、集中荷载以及黏聚力的情况下，采用控制变量的方法对式(27)～(32)进行分析，可知隧道深浅埋侧围岩垂直压力(q1和q2)与隧道拱顶岩土体(BCNM)两侧推力之和(T'1+T'2)呈反比；隧道深浅埋侧围岩水平压力与侧压力系数呈正比。

由式(16)和式(18)可知：变坡段的存在对隧道深埋侧块体ABL的滑动阻力T1以及水平侧压力系数λ1无影响。结合式(29)和式(30)可知，隧道深埋侧水平围岩压力不受变坡段坡度变化的影响。由式(5)、式(22)和式(23)可知：变坡段的存在对隧道浅埋侧块体CDFK的滑动阻力T2和水平侧压力系数λ2均有影响。结合式(27)～(30)可知，变坡段的存在主要影响隧道浅埋侧围岩水平压力以及隧道深、浅埋侧围岩垂直压力。为了进一步定量分析变坡面坡度变化对T2和λ2的影响规律，隧道几何尺寸及力学参数取值与前面的相同，令α3分别为40°，45°，55°和60°，计算并绘制隧道浅埋侧块体CDFK的滑动阻力T2和水平侧压力系数λ2随上变坡面坡度α2变化的影响规律曲线，如图6所示。由图6可知：λ2随上变坡面坡度α2增大逐渐减小；当α3=60°时，T2的降幅为11.69 kPa/(°)，λ2的降幅为0.004 4/(°)；当α3=40°时，T2的降幅为15.81 kPa/(°)，λ2的降幅为0.005 9/(°)，表明T2与λ2的降幅随上变坡面坡度α2增大逐渐增大。结合式(27)，(28)，(31)和(32)可知：随上变坡面坡度α2增大，隧道深、浅埋侧围岩垂直压力逐渐增大，隧道浅埋侧围岩水平压力逐渐减小，隧道偏压现象逐渐变得严重。

图6 上变坡面坡度与滑动阻力以及水平侧压力系数之间的关系曲线Fig.6 Relationship curves of slope of upper slope and sliding resistance,lateral pressure coefficient

令α2分别为5°，10°，20°和25°，计算并绘制隧道浅埋侧块体CDFK的滑动阻力T2和水平侧压力系数λ2随下变坡面坡度α3变化的影响规律曲线，如图7所示。由图7可知：滑动阻力T2及水平侧压力系数λ2随下变坡面坡度α3增大呈先增大后减小的趋势。当α3小于55°时，隧道浅埋侧滑动块体CDFK所占面积随α3增大而增大，体积与质量增加，从而导致T2及λ2增大；当α3大于55°时，隧道浅埋侧滑动块体CDFK所占面积减小，体积与质量减小，从而导致T2及λ2减小。

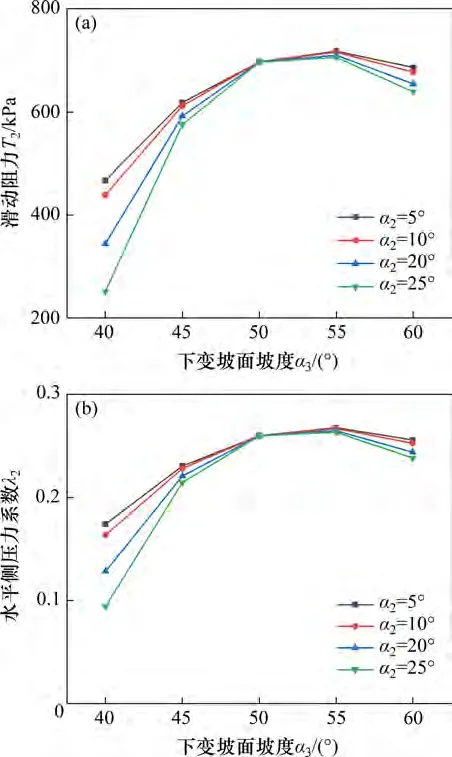
图7 下变坡面坡度与滑动阻力以及水平侧压力系数之间的关系曲线Fig.7 Relationship curves of slope of lower slope and sliding resistance,lateral pressure coefficient

4 工程实例分析

4.1 工程概况

贵广高速铁路某隧道是1 座典型的特大断面隧道。隧道为全长为2 400 m，隧道埋深为2～20 m，开挖跨度为14.7 m，高度为12.5 m，断面面积为150 m2。选取DK592+125～182 为试验段，围岩级别为V 级。该试验段为隧道进口傍山段，存在明显的偏压现象，且山坡较陡，局部采用2次放坡措施来防止山体滑坡[21]。试验监测段主要为全风化泥质砂岩、粉砂岩夹炭质页岩。围岩力学参数取值如下：重度为19.8 kN/m3，弹性模量为43.2 MPa，泊松比为0.33，黏聚力为24.0 kPa，内摩擦角为16.14°。选取监测断面DK592+170，该处围岩属V 级围岩，隧道几何参数取值如下：b=14.7 m，b21=10.5 m，b23=28.7 m，h11=13.5 m，h21=10.5 m，h22=21.5 m，α1=20°，α2=55°，α3=60°。通过埋设在围岩与初支之间的JTM-V2000D型土压力计对初支与围岩之间的接触压力进行监测。在隧道初期支护施作后，接触压力取值为监测压力后期的稳定值。监测断面横断面示意图如图8所示。

图8 监测断面横断面示意图Fig.8 Sketch of cross-section of monitoring section

4.2 监测结果分析

利用修正公式和规范公式计算围岩压力以及现场实测值，如表3所示。由表3可知：对于深埋侧水平压力，修正公式计算值与规范公式计算值相等；对于浅埋侧水平压力与拱顶垂直压力，修正公式计算值比规范公式计算值更接近现场实测值，说明在变坡浅埋偏压情况下，修正公式能够有效考虑因变坡施工而引起浅埋侧岩土体积与质量以及坡度变化对围岩压力的影响。现场实测与规范(修正)公式之间存在差异的原因可能是：现场隧道采用分步开挖法，而规范(修正)计算公式假设隧道全断面一次开挖。

表3 围岩压力计算值与实测值Table 3 Calculated values and monitoring data of surround rock pressurekPa

5 结论

1) 采用极限平衡法推导出了2 次变坡下浅埋偏压隧道围岩压力修正计算公式，并通过与现场实测数据对比分析验证了修正公式的合理性。此外，在对计算条件进行适当简化后，该修正公式可简化为单次变坡下浅埋偏压隧道围岩压力计算公式。

2)变坡段的存在与否不会改变浅埋偏压隧道的偏压效应，由于变坡段的存在，有变坡深埋侧的围岩垂直压力比无变坡的小，水平压力保持不变；有变坡浅埋侧的围岩垂直压力比无变坡的大，水平压力比无变坡的小，表明变坡段的存在对隧道浅埋侧围岩压力影响较大。对比围岩垂直和水平方向的偏压率，变坡段的存在降低了围岩垂直方向的偏压率，增大了围岩水平方向的偏压率，这主要是受隧道浅埋侧滑动岩土体体积和质量变化的影响。

3) 当下变坡面坡度α3一定时，随上变坡面坡度α2增大，隧道浅埋侧块体CDFK的滑动阻力T2和水平侧压力系数λ2逐渐减小，隧道深埋与浅埋侧围岩垂直压力逐渐增大，隧道浅埋侧围岩水平压力逐渐减小，隧道偏压现象逐渐严重。当上变坡面坡度α2一定时，随下变坡面坡度α3增大，隧道浅埋侧块体CDFK的滑动阻力T2和水平侧压力系数λ2呈先增大后减小的趋势，其主要受隧道浅埋侧滑动块体CDFK面积以及体积与质量变化的影响。