基础振动环境下TBM液压空间管道设计方法
2022-01-07赖超张怀亮瞿维熊宇
赖超,张怀亮,瞿维,熊宇
(1. 中南大学机电工程学院,湖南长沙,410083;2. 中南大学高性能复杂制造国家重点实验室,湖南长沙,410083)
液压系统作为TBM(硬岩掘进机)重要的能量传递和控制系统,其工作性能直接影响掘进机传递效率与可靠性[1−2]。空间管道作为TBM液压系统中重要的液压元器件,在强振动环境下长期工作,导致管道振动加剧,管道应力剧增,容易造成管道疲劳破坏。同时,管道振动会造成管内流体大幅波动,给下游液压元件造成冲击,影响管道系统工作效率,因此,有必要对强振动环境下空间管道结构参数进行优化,以提高管道工作性能。
SEGUCHI 等[3]以输流管道的截面形状为优化参数对管道进行优化设计,极大地提高了管道临界流速。HIRAMOTO 等[4]以管道结构参数为优化参数对悬臂输流管道进行设计,以提高管道最大临界流速。SVEDEMAN[5]对管内流体对管壁的侵蚀速度进行优化,改进了冲蚀与腐蚀运行环境下多相流管道设计。BORGLUND[6]对流体流过管道时引起的附加力对管道稳定性的影响进行了优化设计,解决了固定临界流速下管道结构质量最小化问题。BISWAS 等[7]依据充液管系统参数及其流速的关系对管道的平面振动进行优化设计,实现了管道流速的优化。MAALAWI等[8]通过在不增加管道结构质量的前提下对输流管道参数进行优化设计,以提高管道稳定性与避免出现颤振行为。JUNG 等[9]基于遗传算法或粒子群算法与暂态分析技术相结合对输流管道内径设计,研究结果表明可有效改善直管可靠性。WANG[10]通过简化海底输流管道有限元分析模型,提出了一种降低成本的管道设计方法。孙文倩等[11]用有限元的方法分析了基础振动下不同参数对空间管道动力学特性的影响规律。宁海辉等[12]以基础振动参数对直管道最大应力的影响进行优化,制定了以流量−压力−强振动参数为依据的管道抗振结构设计方法。彭欢等[13]运用正交实验法对管道进行结构优化设计,优化设计后的管道系统流速频域幅值整体减小了48.61%。翟红波等[14]以管道结构重量极小化为目标对某类型管道进行了结构优化设计,优化后管道质量减小且抗振能力增强。陈艳秋等[15]运用遗传算法对航空发动机管路进行优化设计,优化后极大地提高了管路抗振动性。王海萍等[16]对管道应力特性进行了分析,并在此基础上提出了管道优化设计方法。张晓玲等[17]对泵源激励下的管道系统进行了振动特性分析,并以管系传到外界基础的功率流最小为优化目标对管道结构参数进行了优化设计。张振华等[18]对基础振动下舰船管道系统动态响应进行了分析,提出了以降低基础振动对于管道系统振动影响的设计方法。李卫等[19]运用遗传算法对随机振动下两端固支直管道结构参数进行了优化设计,设计后的管道最大位移均方值降低了约16.21%,最大应力均方值降低了21.04%。耿艳辉等[20]对大长液压管道的特殊设计进行了研究,提出了管道内径与壁厚的设计方法。
综上所述,国内外对管道设计方法的研究多集中在直管和弯管,很少研究强振动环境下液压空间管道的优化设计。为此,本文作者以减小管道最大应力与流体功率流波动幅值为设计目标,提出基础振动下空间管道设计方法。
1 仿真建模与参数设置
在ANSYS Workbench 中直接建立管道的三维模型,如图1所示。选用相同的网格划分方式对管道以及流体进行网格划分。在Design Simulation中,以管道端面及流体端面作为源面,对管道和流体分别进行扫掠划分。

图1 空间管道模型Fig.1 Space pipeline model
管道内壁定义成流固耦合接触面,管道中间直管段两端固支,激励通过两端的支撑传递给管道,采用简谐激励。流体外壁设置成流固耦合接触面,将沿Y轴方向设置为进口,进口流速设置为5 m/s,沿X轴方向设置为出口。根据TBM 的实际工作情况,设置空间管道系统参数如表1所示。

表1 空间管道系统参数设置Table 1 Parameter setting of spatial pipeline system
2 空间管道应力特性分析
为研究基础振动参数对管道最大应力的影响,使用单因素分析法对不同基础振动方向、频率与振幅下管道最大应力的变化情况进行研究。
2.1 基础振动参数的影响
设置外界基础振动幅值为1 mm,振动频率为20~200 Hz,研究不同基础振动频率对管道最大应力的影响,结果如图2所示。
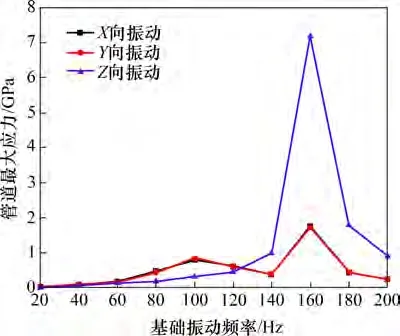
图2 不同基础振动频率对管道最大应力的影响Fig.2 Influence of different foundation vibration frequencies on the maximum stress of pipeline
由图2 可知:基础振动频率在20~160 Hz 时,管道各方向振动最大应力呈增大趋势,在160~200 Hz时,管道各方向振动最大应力呈减小趋势,但不同振动方向的管道最大应力稍有不同;X与Y振动方向下变化趋势基本一致,频率为160 Hz 时管道最大应力峰值最大,且Z方向最大。
设置外界基础振动幅值为0.5~1.5 mm,振动频率为60 Hz。研究不同基础振动幅值对管道最大应力的影响,结果如图3所示。
由图3可知:随基础振动幅值增加,外界输入管道的能量增多,加剧管道振动,使得管道最大应力呈线性增加;X与Y振动方向下变化趋势基本一致,Z向振动最小。

图3 不同基础振动幅值对管道最大应力的影响Fig.3 Influence of different vibration amplitudes of foundation on the maximum stress of pipeline
2.2 管道结构参数的影响
设置外界基础振动幅值为1 mm,振动频率为60 Hz,曲率半径R为25~125 mm,研究X向振动下不同管道曲率半径对管道最大主应力的影响,结果如图4所示。

图4 不同曲率半径对管道最大应力的影响Fig.4 Influence of different curvature radius on the maximum stress of pipeline
由图4可知:随着曲率半径增加,管道模态频率降低,从而接近固有频率,加剧管道振动,使得管道最大应力增加;出口端曲率半径增加对管道最大主应力影响明显大于对进口曲率的影响。
设置外界基础振动幅值为1 mm,振动频率为60 Hz。当管道内径为10~30 mm 时,研究不同管道内径对管道最大应力的影响,结果如图5所示。

图5 不同管道内径对管道最大应力的影响Fig.5 Influence of different pipe inner diameters on the maximum stress of pipeline
由图5可知:随管道内径增加,管道模态频率增加,从而远离基础振动频率,降低管道振动,使得管道最大应力减小。
设置外界基础振动振动幅值为1 mm,振动频率为60 Hz。当管道壁厚分别为3 mm 与9 mm 时,研究X向振动下不同管道壁厚对管道最大主应力随时间变化,结果如图6所示。
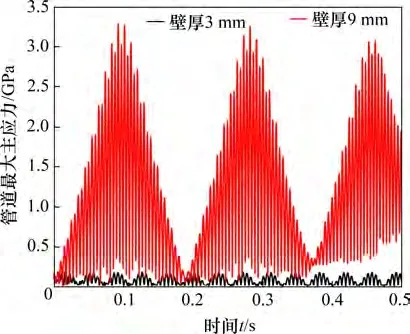
图6 不同管道壁厚对管道最大应力的影响Fig.6 Influence of different pipe wall thicknesses on the maximum stress of pipeline
由图6可知:随管道壁厚增加,管道模态频率降低,靠近基础振动频率,加剧管道振动,从而管道最大主应力增加。
3 空间管道流体功率流分析
3.1 流体功率流模型的建立
分析振动时,传统方法一般是采用应力或者速度等某个单一物理量来衡量结构振动特性响应,但往往会忽略它们之间的联系[21],应用功率流的研究方法综合考虑应力和速度更能反映管道流体能量的传递效率和稳定性。功率Pi即单位时间内做功的能力,其表达式为

其中:Fi为结构上第i节点所受的作用力;vi为第i节点速度。对于管道结构,运用有限元法,其单个节点在某一时刻的功率Pi为

其中:Px,Py和Pz分别表示节点在x,y与z方向上的功率流。
假设流体界面有n个单元节点,则某时刻流体某截面的总功率P为

时间T内流体平均功率为

其中:fi(t)与vi(t)分别为时刻t节点i所受的作用力与速度。
3.2 基础振动参数的影响
设置基础振动幅值为1 mm,当基础振动频率在60~100 Hz之间变化时,研究X向振动下不同基础振动频率对管道出口流体功率的影响,结果如图7所示。
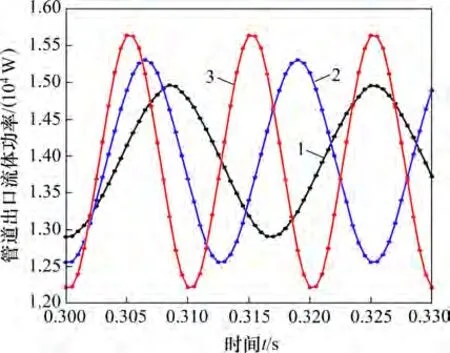
图7 不同振动频率对出口功率流的影响Fig.7 Influence of different vibration frequencies on power flow at outlet
由图7可知:管道出口流体功率流随时间呈周期性波动,波动周期与基础振动周期一致;随着基础振动频率增大,流体平均功率稍有降低,流体能量损失增加,传动效率降低;出口流体功率波动幅值增加,越接近管道模态频率,管道振动加剧,管道越不稳定。
设置基础振动频率为100 Hz,当基础振动幅值在1.0~1.5 mm 之间变化时,研究X向振动下不同基础振动幅值对管道出口流体功率流的影响,结果如图8所示。
由图8可知:随着基础振动振幅增加,平均功率降低,流体能量耗损增加,传动效率降低,但流体功率流波动幅值增加,管道固有频率减小,接近基础振动频率,从而增强下游执行元件的不稳定性。

图8 不同振动幅值对出口功率流的影响Fig.8 Influence of different vibration amplitudes on outlet power flow
3.3 管道结构参数的影响
设置外界基础振动幅值为1 mm,振动频率为100 Hz,曲率半径R分别为50,75 和100 mm,研究X向振动下管道曲率半径对出口流体功率的影响,如图9所示。
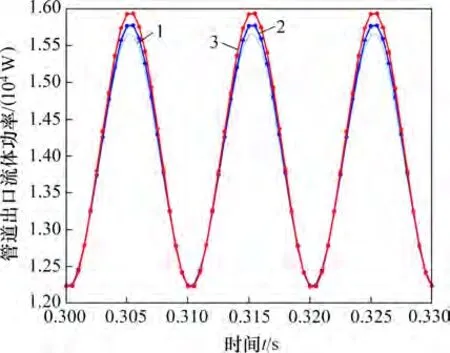
图9 不同曲率半径对出口功率流的影响Fig.9 Influence of different radius of curvature on outlet power flow
从图9可知:随着曲率半径增加,降低因流体流动方向改变所耗损的能量,使得流体的平均功率增加,传递效率增加;管道模态频率减小,导致管道模态频率接近基础振动频率,管道振动加剧,进而增大流体功率波动幅值,管道越不稳定。
设置外界基础振动幅值为1 mm,振动频率为100 Hz。保持管道壁厚不变,当管道内径分别为13,19 和25 mm 时,研究X向振动下不同管道内径下出口流体功率的影响,结果如图10所示。
从图10 可知:随着管道内径增加,流体波动周期内平均功率增加,单位时间内流体通流面积增加,传递能量增大,传动效率增加,但管道模态频率降低,接近基础振动频率,加剧管道振动,从而管道流体功率的波动幅值大幅度增加,管道稳定性降低。

图10 不同管道内径对出口功率流的影响Fig.10 Influence of different inner diameters of pipe on outlet power flow
设置外界基础振动振动幅值为1 mm,振动频率为100 Hz。当管道壁厚分别为3 mm与9 mm时,研究X向振动下不同管道壁厚对出口流体功率的影响,结果如图11所示。

图11 不同管道壁厚对出口功率流的影响Fig.11 Influence of different pipe wall thicknesses on outlet power flow
从图11 可知:随着壁厚增加,管道固有频率增加,流体平均功率流增加和波动幅值降低,从而有利于提高管道流体传递效率,增加管道稳定性。
4 基础振动下液压空间管道设计
在外界基础振动作用下,管道结构参数不同,空间管道振动特性存在明显差异,严重影响管道最大主应力及流体功率流,因此,有必要对基础振动下管道结构参数进行优化,以提高管道振动环境下的性能。
管道结构参数变化会同时对管道多个性能产生重要影响,因此,基础振动下管道的结构参数优化是一个多目标优化问题。由于管道的结构参数和管道振动性能之间具有很强的非线性,得出函数关系较困难,故本文应用综合评分法建立优化目标与因素之间的数学模型,利用单因素分析法对管道结构参数优化,以提高管道振动稳定性,减小管道应力,同时尽量减小流体功率流波动幅值。
4.1 管道优化模型的建立
综合评分公式为

式中:yi为第i号实验综合评分;ak为第k项指标的评分系数;ck为第k项指标的扩大系数。针对各项指标量纲不一致的问题,应用优化前管道各指标数值对综合指标进行归一化处理,其评分J计算公式为

式中:σ0为优化前管道最大应力;P0为优化前流体功率流波动幅值。
由于管道长度小,管道结构参数的变化对流体平均功率的影响小,并且相比管道出口压力,流体功率流波动幅值更能反映流速与压力之间的关系,因此,指标选择管道最大应力与功率波动幅值。
确定指标后,需要对指标设置权值。由前面的分析可知,相比无基础振动,在基础振动下,管道最大应力与功率波动幅值均会增加。管道最大应力增加,会使得管道容易出现损坏,产生安全事故。虽然流体功率流波动幅值增加会使下游推进元件工作不稳定,但其产生的影响并不会导致安全事故发生,因此,基础振动下管道的设计是着重减小管道应力。
设置评分系数ck为100,根据优化指标的重要性,将权值rk分别设置为r1=0.08,r2=0.02,因此,优化评分J计算公式为

管道最大应力与流体功率流波动幅值越小越好,因此,综合评分值J越小,管道的综合特性越好。
4.2 优化结果分析
采用单因素法分析管道结构参数对综合评分的影响时,忽略了各因素之间的相互作用,因此,需要考虑各结构参数之间的交叉作用对实验结果的影响,采用正交实验法对空间管道结构参数进行优化,实现多因素试验,寻求最优水平组合,高效确定影响管道特性结构参数因素的主次顺序、最佳管道结构参数组合,以最大限度地提高管道综合特性。
正交实验以液压空间管道曲率半径、内径及壁厚3个结构参数作为影响因素。设置外界基础振动幅值为1 mm,基础振动频率为100 Hz,振动方向为X向,其他因素保持不变,试验因素水平如表2所示。

表2 因素水平表Table 2 Factor level table
根据正交试验设计方案,确定因素水平后,本实验通过分析选用正交表为L9(34),此外,依据正交表确定试验各参数组合正交实验,实验结果如表3所示。
极差R越大,说明该因素对试验结果的影响也越大。由表3可知对管道综合特性的主次顺序依次为A,C和B。采用试验指标均值为Y轴,因素水平为X轴,因素水平与实验指标的关系如图12所示。

表3 正交实验方案和实验结果Table 3 Orthogonal experiment schemes and experimental results
由图12 可知:为了使管道的振动特性达到最佳,管道的结构参数应为A2B2C2,但正交表中没有对A2B2C2方案进行试验,正交表中使管道振动特性最佳的管道结构参数为A2B2C3,因此,需要再次通过试验来验证。对方案A2B2C2进行试验,得到该方案下管道综合评分值为76.228,综合评分大于试验方案中A2B2C3的评分,说明方案A2B2C3是最佳方案。

图12 因素水平与指标综合得分关系Fig.12 Relationship between factor level and test index
将方案A2B2C3对应的管道结构参数代入仿真,得到优化后的管道应力与流体功率波动幅值,如图13与14所示。
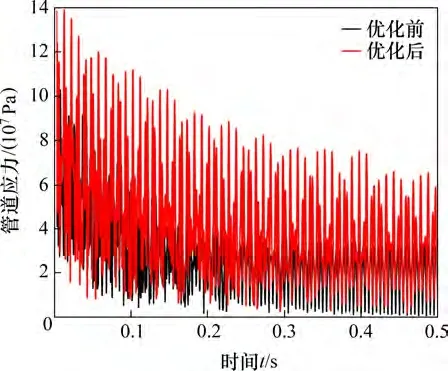
图13 优化前后管道应力对比Fig.13 Comparison of pipeline stress before and after optimization
从图13 可知:优化后管道应力大幅度减小,减小了56.27%。从图14 可知优化后管道综合性能得到提升。

图14 优化前后出口功率流对比Fig.14 Comparison of outlet power flow before and after optimization
4.3 管道设计流程
综上可知,管道的振动特性由管道的结构参数与基础振动参数决定。在TBM 上破岩掘进工作过程中,长期存在基础振动影响,传统设计方法已不能适应TBM 上管道结构的设计要求,因此,有必要提出基础振动下空间管道的设计流程,优化管道结构参数,提高管道工作性能。基础振动下液压空间管道设计流程如图15所示。
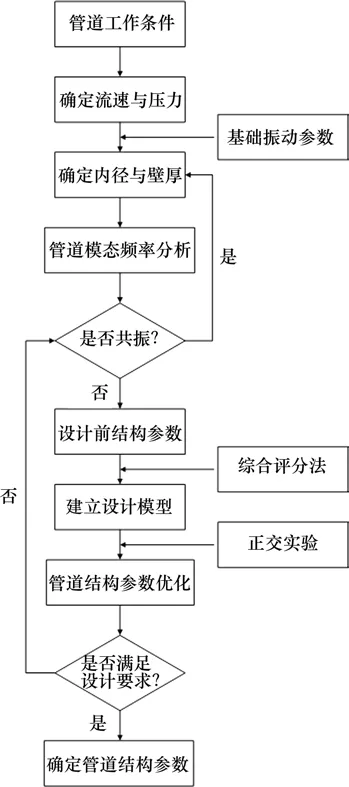
图15 基础振动下液压空间管道设计流程Fig.15 Design process of hydraulic space pipeline under foundation vibration
5 结论
1)建立了基础振动下液压空间管道仿真模型与流体功率流数学模型。随着频率和幅值增加,管道最大应力逐渐增加;随着曲率半径和壁厚增加,管道模态频率降低,管道振动加剧;随管道内径增加,管道模态频率增加,管道振动减小。
2)确定了管道结构参数影响综合特性的主次顺序和最佳结构参数组合,在该最佳结构参数组合下,优化后管道最大主应主力减小56.27%,在此基础上提出基础振动下液压空间管道设计流程,能有效改善强振动环境下管道工作性能。
