基于Shapley值组合模型的电力需求预测研究

王欣，谢文华，张利君

（东北电力大学经济管理学院，吉林 吉林 132000）

0 引言

随着我国经济快速增长，地区电力需求也呈现新的波动特征。传统的预测模型不能将用电量数据与电力需求的宏观影响因素有效融合，难以对新形势下地区电力需求进行合理判断。因此，深入研究电力需求预测模型对电网的科学规划与合理投资具有重要意义。已有学者对电力需求的预测进行了研究。一些学者应用历史用电量数据的时间序列变化规律对地区电力需求进行预测。例如田星等基于适应“S”形增长的动态灰色Verhulst模型对宁夏回族自治区的电力需求进行预测[1]；史静等通过对江苏省各区域用电量增速及电力消费弹性系数的探讨，对“十三五”期间江苏省电力需求进行分析[2]；陈宝平构建优化的灰色马尔科夫模型对内蒙古自治区的电力需求展开预测[3]。还有一些学者基于对电力需求影响因素的分析对其进行预测。例如夏翔等基于经济发展、人口与社会发展、电网结构与管理水平等指标，利用灰色模型叠加小波分解结果对电力需求进行预测[4]；黄元生等采用PSO算法对协方差函数中的参数进行优化，将修正后的参数作为初始值构建GPR电力需求预测模型[5]；田书欣等从经济、产业、用电环境等方面对电力需求的影响因素进行分析，并基于PIO-SVM模型对区域电网的电力需求展开预测[6]。

虽然有关电力需求的预测方法较多，但未能将原始用电量数据与其影响因素在电力需求预测中的重要程度进行综合考虑。基于此，本文提出了一种基于Shapley值的组合预测模型，将两类预测方法有效结合，通过对基于原始用电量数据的GM预测模型和基于电力需求关键影响因素的PSO-ELM预测模型赋予不同的权重，得到集结更多有用信息的电力需求组合预测模型。

1 电力需求的影响因素分析

为了对电力需求进行更为合理、准确的预测，首先需要对其主要影响因素进行分析。为此，梳理了包含GDP、城镇化率、全社会固定资产投资、居民消费水平以及能耗强度在内的关键影响指标。

1.1 GDP

电力需求水平的提升是地区经济增长所必需的生产要素，一般以GDP衡量地区经济的发展水平，而经济增长又是电力需求水平提升的必要条件。只有在经济发展向好的前提下，才能为电力设施投资规模的进一步扩大、电力供应质量的提高提供资金保障，推动地区用电量的稳步增长。

1.2 城镇化率

随着社会的不断发展，城市化进程的加快将创造出巨大的电力工业基础设施建设与投资需求，对地区电力需求空间的分布产生一定的影响。相关研究表明，我国城镇化率从50%提升到75%的进程中，每提高1%，全社会用电量增加4.6%左右；当城镇化率超过75%后，电力需求的增长会相对放缓[7]。

1.3 全社会固定资产投资

地区固定资产的建设要以能源消耗为基础，而电力作为近年来能源消费的主力军，其消费水平与固定资产的投资力度基本保持着正相关关系。

1.4 居民消费水平

在经济社会稳步发展的同时，居民对生活质量改善的期望也呈增长趋势。不仅提高了其在能源消费领域对清洁电力的认可度，也拓宽了在电动汽车、家用电器等领域的新兴用电方式[8]。

1.5 能耗强度

近年来为兑现节能减排承诺，以单位GDP能源消耗（即能耗强度）为核心指标建立的低碳经济发展目标体系，将以推动绿色电力消费为首要举措，营造出更为健康的能源消费及经济增长环境。

2 模型构建

2.1 灰色关联度

灰色关联度模型是通过系统中各指标的已知信息得出演化规律，其主要步骤如下[9]。

（1）确定反映系统总体行为的参考序列X0，X0={X（01），X（02），…，X（0k），…，X（0n）}，以及影响系统行为的m个比较序列Xi，Xi={X（i1），X（i2），…，X（ik），…，X（in）}，其中，i=1，2，…，m；k表示不同时刻，k=1，2，…，n。

（2）对各指标进行无量纲处理后，计算每个比较序列与参考序列对应分量的绝对差值，即|X0(k)-Xi(k)|，k=1，2，…，n；i=1，2，…，m。进而得到两级差值为、|。

（3）由式（1）和式（2）分别计算得到第s个样本与正理想样本关于第t个指标的灰色关联系数ξi和关联度γi。

式中：ρ为分辨系数，一般为0.5。

2.2 单一预测模型

2.2.1 GM（Grey Model）预测模型

由最小二乘法得到GM（1，1）模型参数：

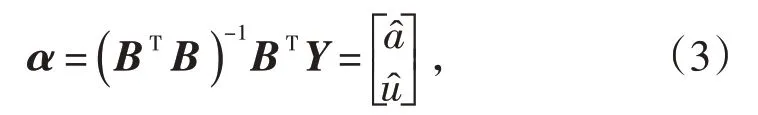
式中：Y为数据向量；B为数据矩阵；BT为矩阵B的转置矩阵；u为参数，û为u的估计值；a为发展系数，â为a的估计值。

进而得到时间响应序列为：

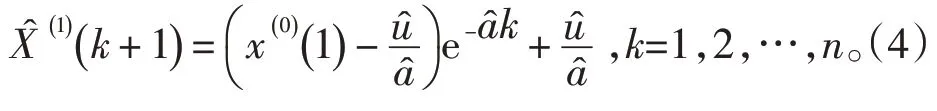
将方程累减还原后得到原始序列的预测模型为[10]：

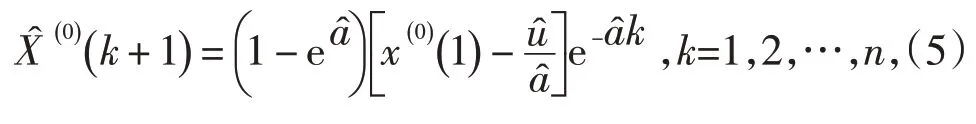
2.2.2 PSO-ELM模型

2.2.2.1 极限学习机

极限学习机（Extrem Learning Machine，ELM）是一种单隐含层前馈型神经网络算法[11]。设隐含层的激活函数为g(x)，输入层有n个神经元，隐含层有l个神经元，输出层有m个神经元，输入层与隐含层间的连接权值为ω，Q为训练集的样本数，则ELM网络模型表示为：

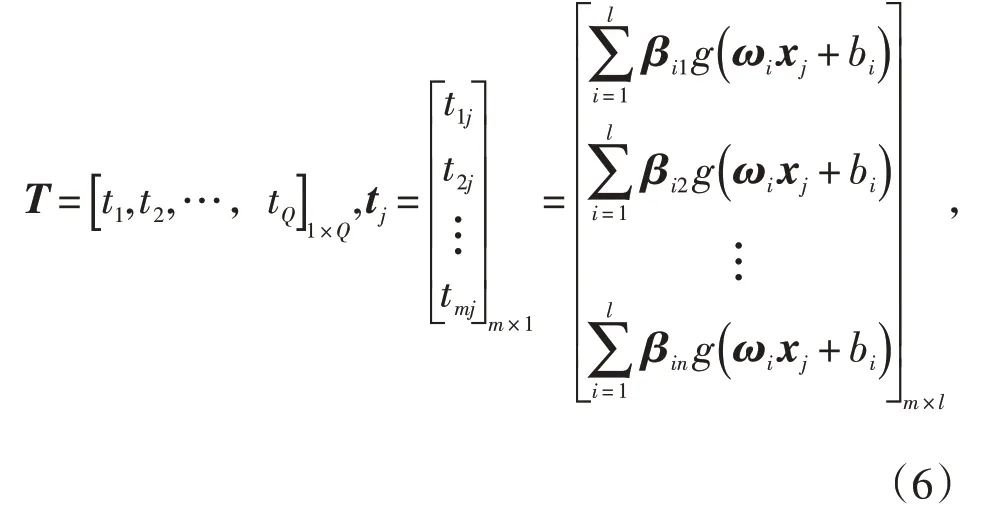
将式（6）简化为Hβ=TT，TT为矩阵T的转置，H为神经网络的隐含层输出矩阵，其具体表达式为：

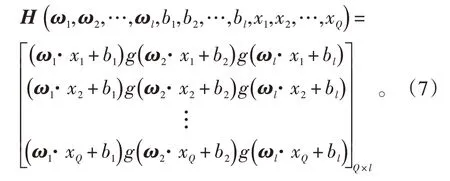
则隐含层与输出层间的连接权值为:

2.2.2.2 粒子群优化算法

粒子群优化算法（Particle Swarm Optimization，PSO）利用粒子的寻优优化能力，在一定范围内对ELM网络的最优连接参数进行搜索，避免了ELM随机产生输入层权值和隐含层阈值所造成的不稳定性，从而改善模型的预测精度。在每一次的迭代更新过程中，粒子通过个体极值和全局极值更新自身的速度和位置，其更新表达式为[13]：

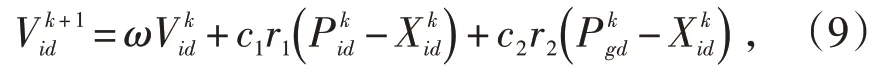
式中：w为惯性权重；k为当前迭代次数；Vid为粒子的速度；c1、c2为加速度因子；r1、r2为分布于[0，1]间的随机数；为第i个粒子在D维搜索空间的位置；为种群的全局极值，d=1，2，…，D；i=1，2，…，n。

PSO-ELM的算法流程见图1。

图1 PSO-ELM算法流程图

2.3 组合预测模型

Shapley值多用于合作博弈中利益分配问题的探讨，它最大的优点是其原理和分配结果易于被各利益相关主体视为公平并选择接受。根据Shapley值在收益分配中的应用，可将各单一预测方法共同作用所产生的组合预测总误差视为收益，根据各方法的“合作关系”，将该收益值在不同预测方法中进行分配，即确定每种预测方式在组合预测模型中所占的权重[14]。

假设N={1，2，…，n}为n种方法的集合，S、T为N的任意子集，E（S）、E（T）为各自组合的误差，并且有E（S）+E（T）≥E（S∪T）。令yi为第i种方法的分配误差，且yi≤E（i），则n种方法组合预测后的总误差将在n中完全分摊[14]，即。

若i种方法的绝对误差平均值为Ei，组合预测的总误差为E，则：

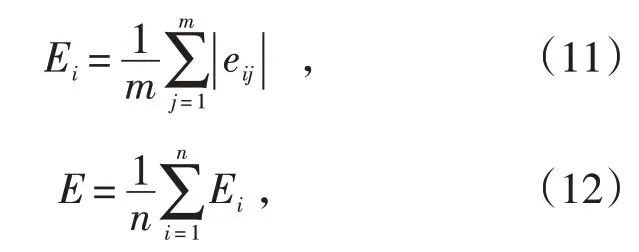
式中：m为样本数；|eij|为第i种方法对样本j的绝对误差值。

则Shapley值赋权公式为：

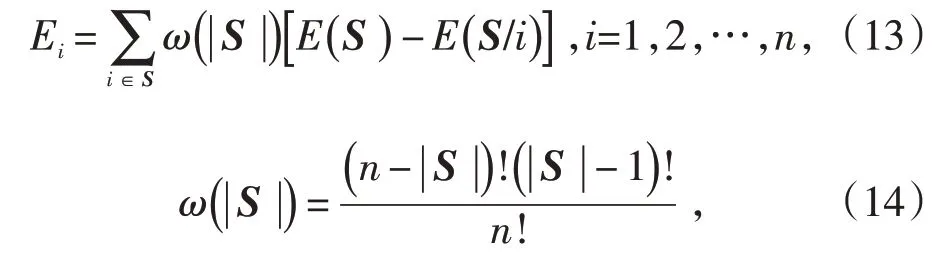
式中：ω(|S|)为单个预测方法i的边际贡献；|S|为S子集的个数；E(S/i)为子集S除去i后的绝对误差值[15]。则第i种方法的权重计算表达式为：

3 算例分析

针对上述对电力需求影响因素的分析和预测模型的探讨，以吉林省为例，选取2005—2015年的数据为训练集，2016—2020年的数据为测试集，利用MATLAB R2018a对该地区“十四五”期间的电力需求进行预测。

3.1 电力需求的关键影响因素分析

基于灰色关联度理论对该地区电力需求的关键影响因素进行筛选。收集吉林省2005—2020年GDP、全社会固定资产投资、居民消费水平、城镇化率及能耗强度的相关数据（见表1），将用电量作为参考数列，各项指标作为比较数列，以初值化法对其进行无量纲化处理后，根据式（1）和式（2）分别计算关联系数矩阵及灰色关联度，计算结果见表2。

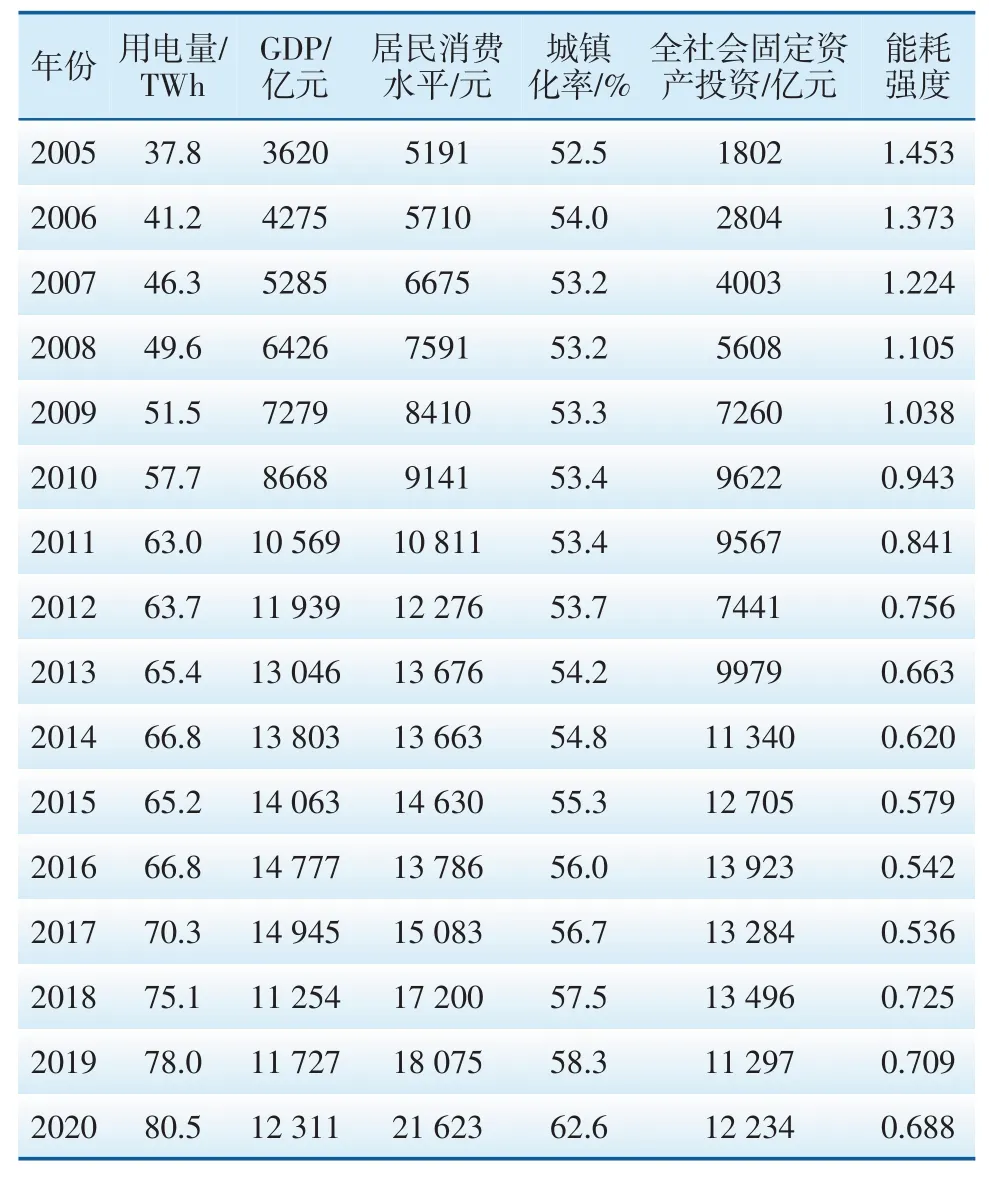
表1 电力需求的关键影响因素

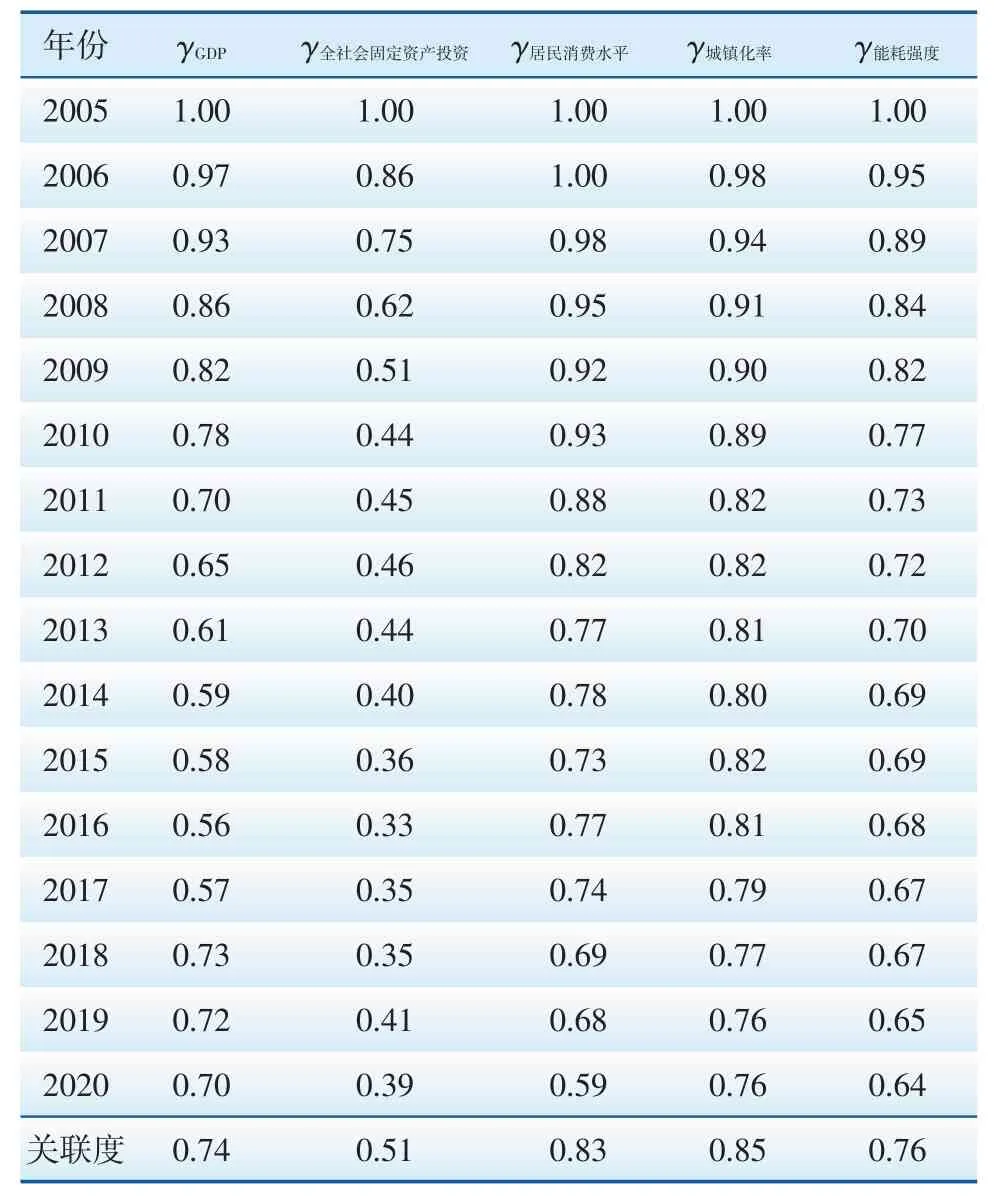
表2 用电量关联系数矩阵及灰色关联度

各比较数列的灰色关联度均大于0.5，说明所选取的指标科学合理，对吉林省电力需求均具有一定的影响。从关联度的大小来看，其关联序为城镇化率＞居民消费水平＞能耗强度＞GDP＞全社会固定资产投资，前四项指标的关联度均大于0.7，明显高于全社会固定资产投资对吉林省电力需求的影响。因此，为提高预测的精度及可靠性，以城镇化率、居民消费水平、能耗强度和GDP作为吉林省电力需求的强关联影响要素对其进行预测。

3.2 基于组合模型的电力需求预测

为对比模型的性能，引入平均绝对百分比误差（MAPE）对模型的仿真效果进行评价，即：

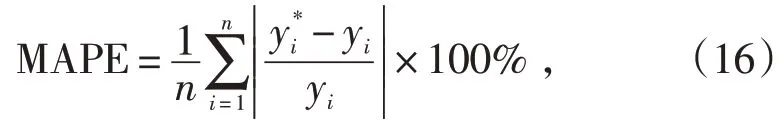
利用GM预测模型进行预测，根据式（3）—式（5），得出模型参数和时间响应序列分别为：

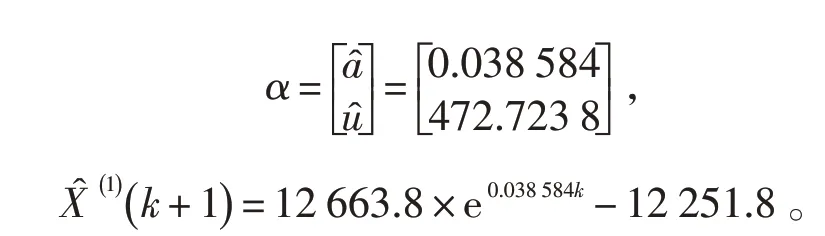
根据累减还原后的原始预测模型得到测试集中每个年份MAPE值，其计算结果见表3。

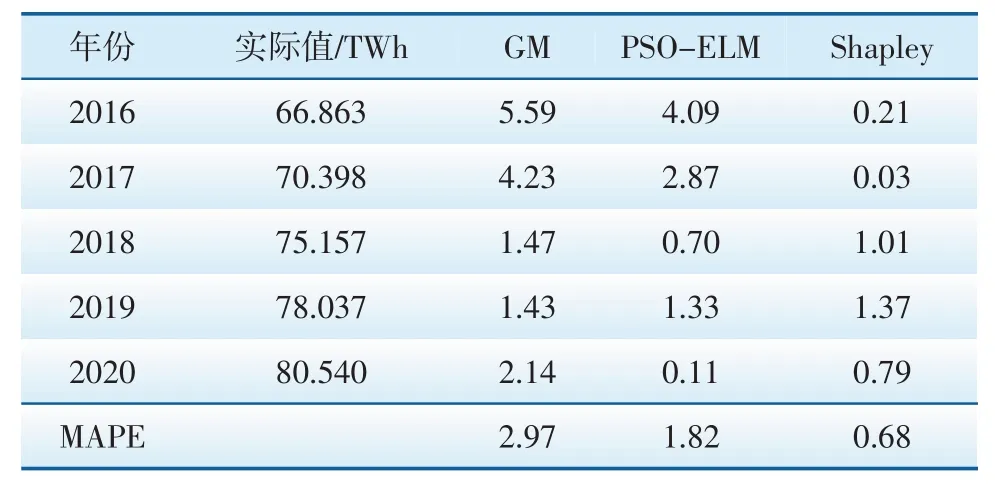
表3 GM、PSO-ELM及Shapley值组合预测模型MAPE对比

同时，对构建的PSO-ELM模型进行参数设定，初始化粒子种群规模M=20，学习因子C1=C2=2，惯性权重系数ωmax=0.9、ωmin=0.2，[Vmin，Vmax]=[-1，1]，最大迭代次数T=100。将各指标的原始数据作为输入变量对模型进行训练，得到PSO-ELM的寻优曲线（见图2）。从图中可以看出，粒子的平均适应度总体处于下降趋势，最佳适应度在前55次迭代中呈阶梯状下降，而后基本保持不变，在第90次迭代时又出现新的下降拐点，至迭代结束，其最优适应度值已接近于所设定的0.01精度，表现出PSO算法强大的寻优能力。为对比经PSO优化后的ELM模型在最优的网络结构下是否具有更好的预测性能，分别对PSO-ELM和ELM模型进行仿真，得到的测试结果见图3。从图中可以看出，PSO-ELM模型预测值与实际值的拟合优度明显优于ELM模型，即PSO算法有效改善了ELM模型的可靠性，提升了预测精度。

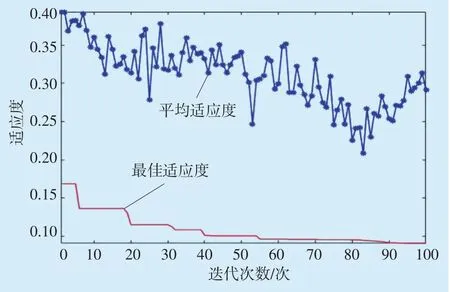
图2 PSO-ELM寻优曲线

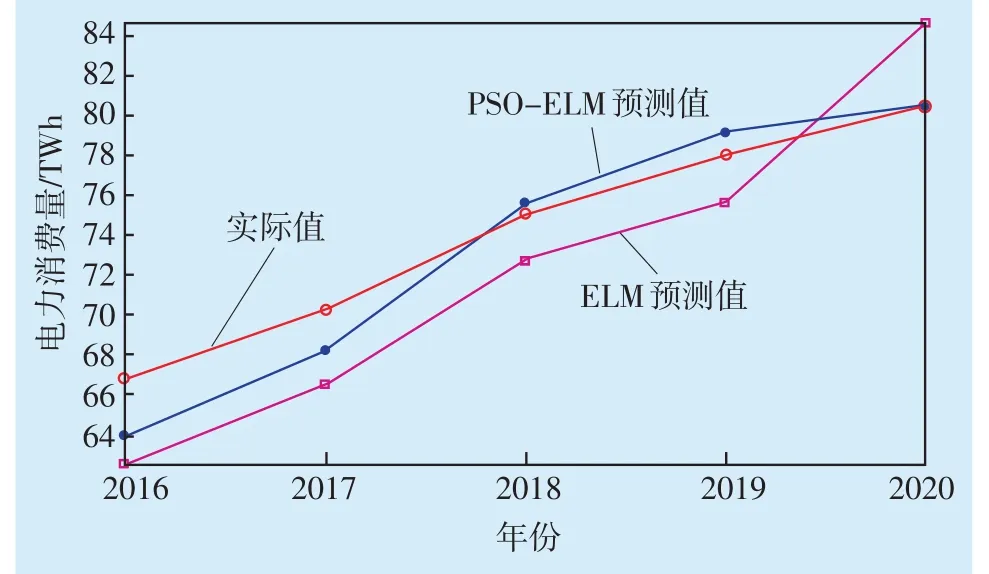
图3 PSO-ELM和ELM模型仿真图

基于对Shapley值理论的探讨，进一步对GM、PSO-ELM所构建的组合预测模型进行分析。参与组合预测模型总误差分配的成员为N={1，2}，1、2分别代表GM和PSO-ELM模型，E（1），E（2），E{1，2}的数值代表绝对误差均值。根据式（13）和（14）求得各成员的Shapley值为E1=12.765、E2=8.525；进而由式（15）确定其权重分别为w1=0.400 4、w2=0.599 6。由此，得到的组合预测模型为：

式中：y1t为GM模型的预测值；y2t为PSO-ELM模型的预测值；t为年份。

由式（17）计算Shapley组合预测模型的MAPE值（见表3）。由表3可知，在单一预测模型中，PSO-ELM模型的预测精度优于GM模型，其测试样本的相对误差均低于GM模型；而经Shapley值重新分配权重后的组合预测模型MAPE值仅为0.68，明显低于各单一预测模型。可见，相较于GM、PSO-ELM两种单一预测模型，组合预测方法具有更高的精度，在电力需求预测的应用中更为有效。因此，利用该模型对吉林省“十四五”期间的电力需求进行预测，结果见表4。

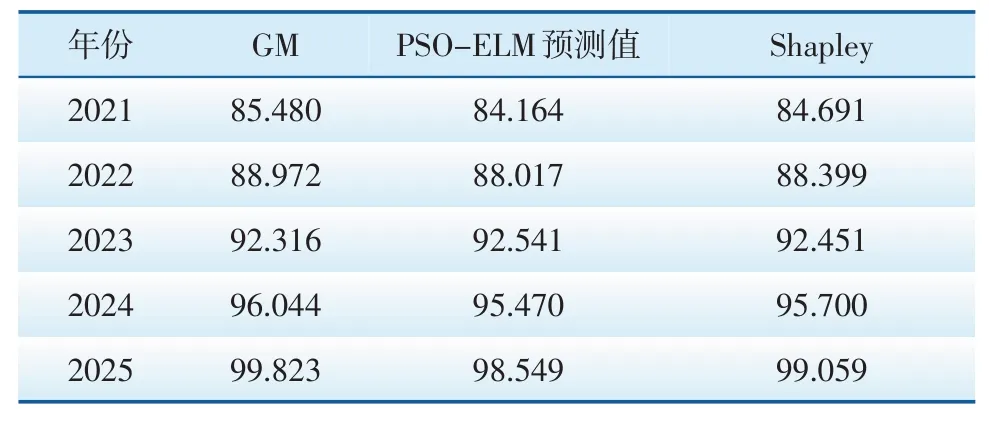
表4 吉林省“十四五”期间电力需求预测 TWh

4 结束语

本文在两种单一预测方法的基础上，构建了基于Shapley值的组合预测模型。通过误差对比可知，该模型充分考虑单一预测模型的优势，有效提高整体预测精度，为地区电力需求预测提供了新思路。因此，由该组合赋权预测模型得到的吉林省“十四五”期间电力需求的预测结果，可在一定精度上为当地电力部门的相关规划提供参考。