一类具有饱和恢复率的随机传染病模型

刘 娟，陈 功

(蚌埠学院理学院，安徽蚌埠 233030)

传染病是当今世界面临的一个严重问题，传染病的蔓延给世界各国带来了极大的挑战，甚至可能影响社会稳定，比如新冠病毒的传播给现实生活造成了一定的影响，因此研究传染病模型具有重要的实际意义。随着传染病动力学的深入发展，建立数学模型研究传染病的传播规律已成为一种趋势。近二十年来国内外学者根据仓室模型的思想，提出了大量的传染病模型并研究了模型的动力学性质。在已建立的传染病模型中，以确定型模型居多[1-6]。但是在疾病蔓延的过程中，外部环境对疾病传播有着重要的影响，这在数学上可以用随机扰动项来表示。文献[7]研究了下列传染病模型：

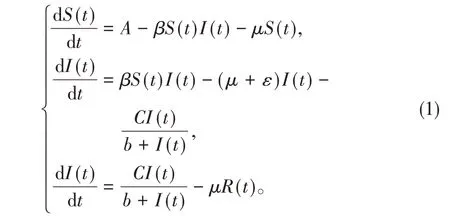
根据仓室建模的思想，(1)式中的，S(t)，I(t)和R(t)分别表示易感者、染病者、治愈者群体在时刻t的数量[8-9]。A表示易感者群体的常数输入率，μ为，S(t)，I(t)和R(t)的自然死亡率，假设三类群体具有相同的自然死亡率。ε为染病群体的因病死亡率。为染病群体到治愈群体的恢复率函数。文献[7]研究了模型(1)的稳定性和分支。

考虑到随机扰动因素对疾病传播的影响，在模型(1)中引入随机扰动项使之变成随机微分方程，假设外部环境主要影响参数β，用白噪声来描述这种影响，即

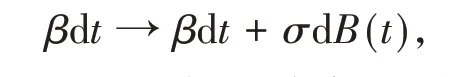
B(t)为标准布朗运动且B(0)=0，为白噪声强度，则得到下列具有随机扰动项的传染病系统，

主要研究随机传染病的动力学性质，包括模型(2)正解的存在性I(t)及和R(t)群体的灭绝性。

1 模型(2)正解的存在唯一性

生物系统的动力学性质有多种，对于传染病系统，是否具有全局正解是很重要的，由随机微分方程解的存在唯一性定理知，若系统满足局部利普希茨条件和线性增长条件，则具有唯一的正解。通过利用Lyapunov方法证明模型(2)具有唯一的全局正解。

定理 1对于任意给定的初值X(0)=(S(0),I(0),R(0))，系统（2）在t≥0 上存在唯一的解，且该解以概率1 存在于中，即系统(2)在中存在唯一的全局正解。

证明易知模型(2)满足局部利普希茨条件，则对任意的初始条件，模型(2)存在唯一的局部解X(t)(t∈[ 0,τe])，其中τe是系统的爆破时间。证明X(t)(t∈[ 0,τe])是模型(2)的全局正解，为了证明该结论，只要证明τe∈∞a.s.即可。

设足够大的正数k0≥1，能使X(0)都位于区间中，再k≥k0设，定义停时

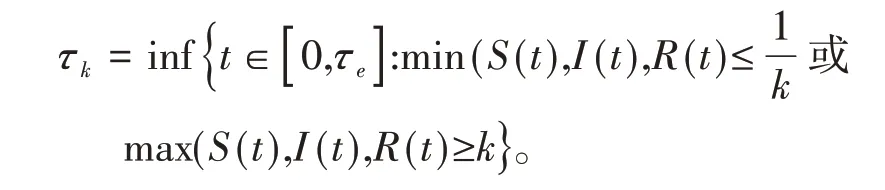
规定inf ∅=∞，易知τk是k的单调增函数，设，得τ∞=τe∞a.s.，若能证明τ∞=∞，则τe=∞且X(t) ∈(t＞0)。故利用反证法的思想证明τ∞=∞，若τ∞≠∞，则存在常数T＞0 及ε∈(0,1)，使得P{τ∞≤T}τ∞＞ε成立，则存在正数k1≥k0，对所有的k≥k1，有

将模型(2)相加，得

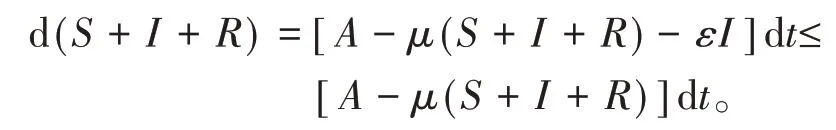
由方程初值X(0)=(S(0),I(0),R(0))，可求得

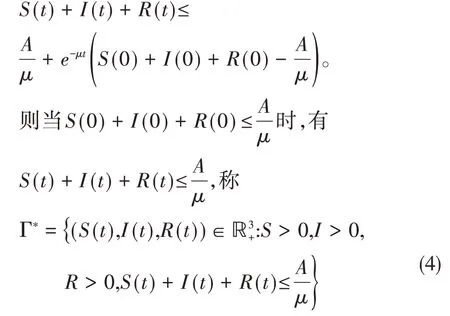
为正不变集。

定义

令T=0，则对任意，使用Itô公式计算得

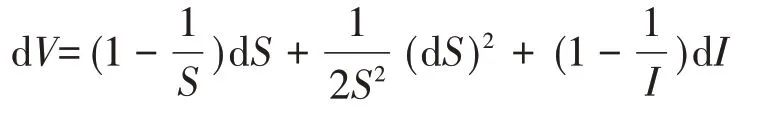
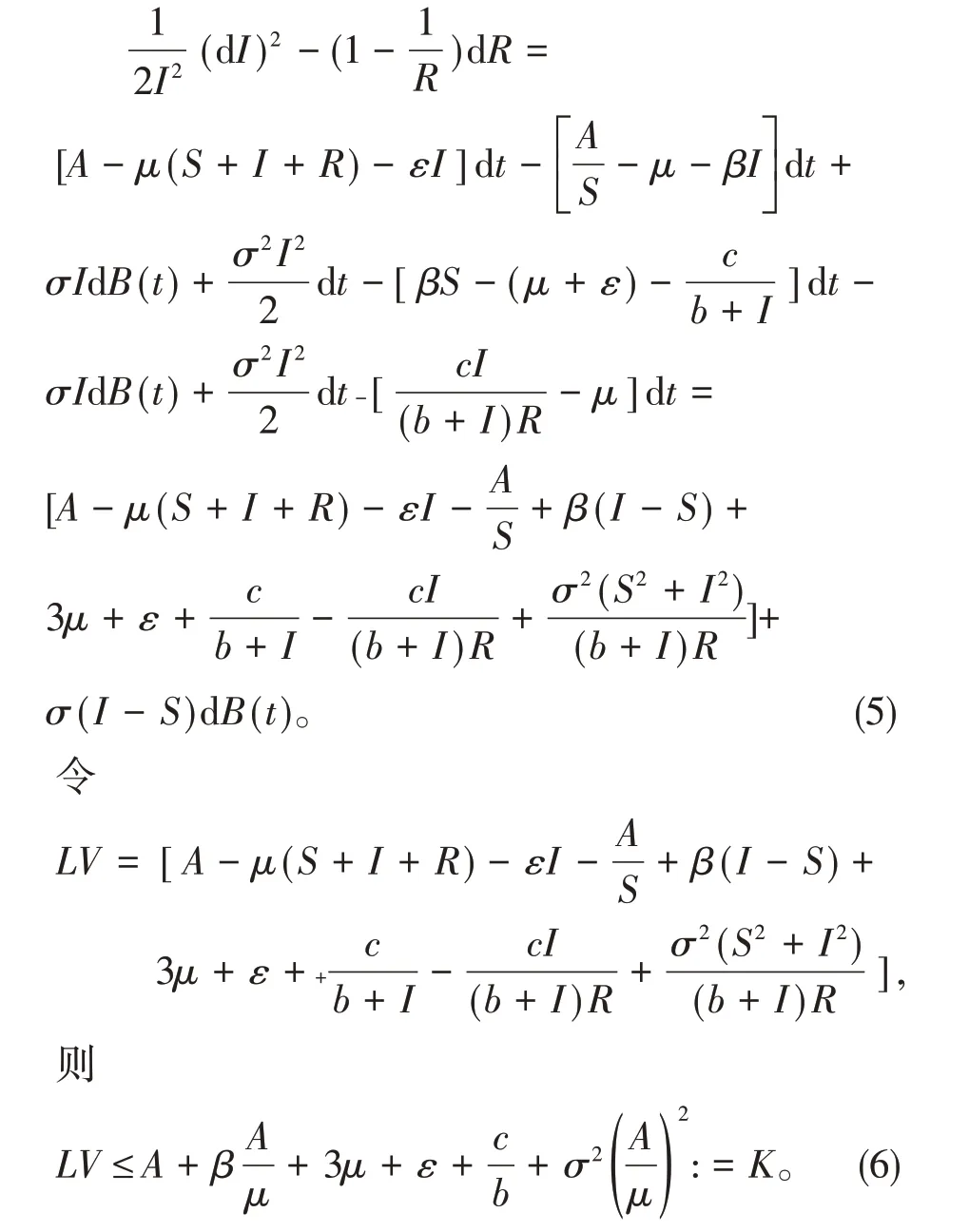
将(6)式代入dV的表达式得

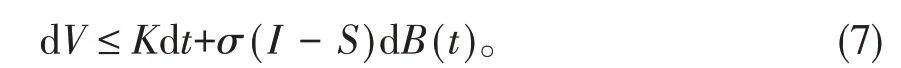
对(7)式两边取0到的积分，再取数学期望得

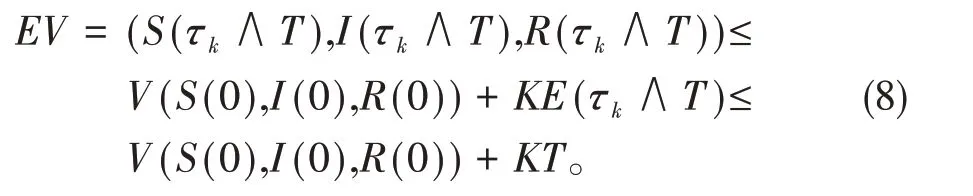
对所有的k≥k1，有P{τk≤T}＞ε。对于每一个ω∈{τk≤T}，S(τk,ω)，I(τk,ω)，R(τk,ω)中至少有一个等于k或，故有

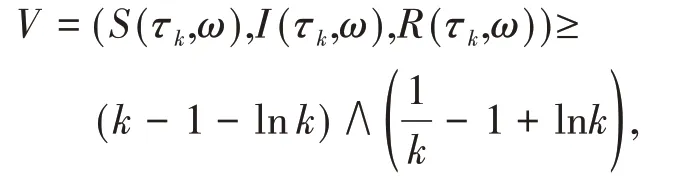
利用(8)可得

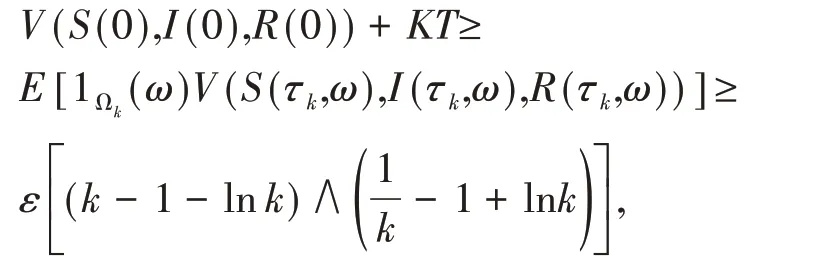
其中Ωk={τk≤T}，1Ωk(ω)为Ωk的示性函数，令，有k→∞，

由此可知，假设不成立，故τe=∞a.s.，即模型(2)存在唯一的全局正解。

2 模型(2)疾病的灭绝性

讨论在模型(2)中，染病群体及治愈者群体的灭绝条件，假设系统初始条件满足X(0) ∈Γ∗，其中Γ∗为为系统(2)的正不变集。

定理2设为模型(2)的解，对于任意给定初始条件，若

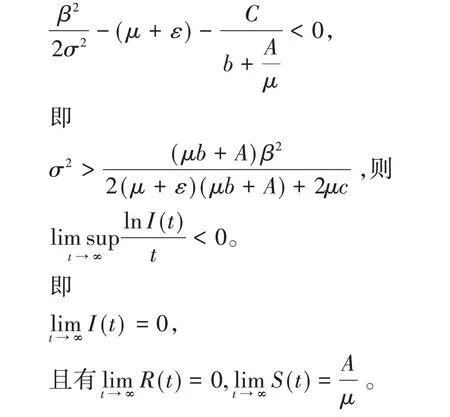
证明利用Itô公式，将模型(2)中含有染病群体的项改写为

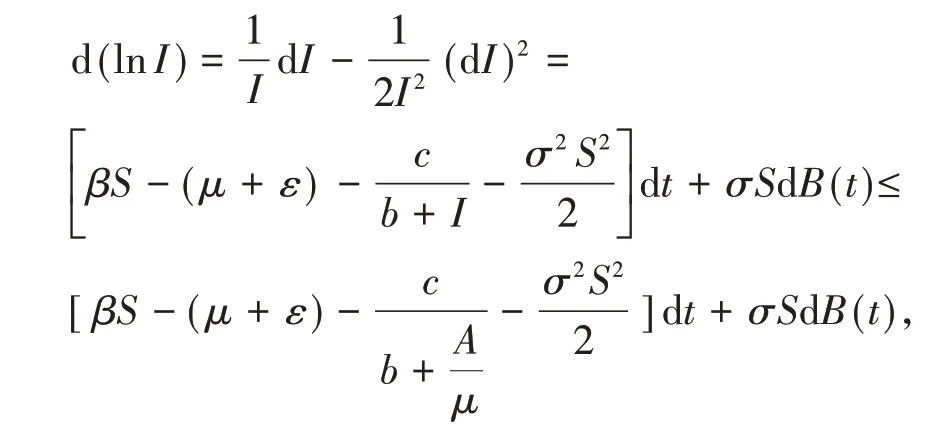
两边从0到t积分，并除以t，记

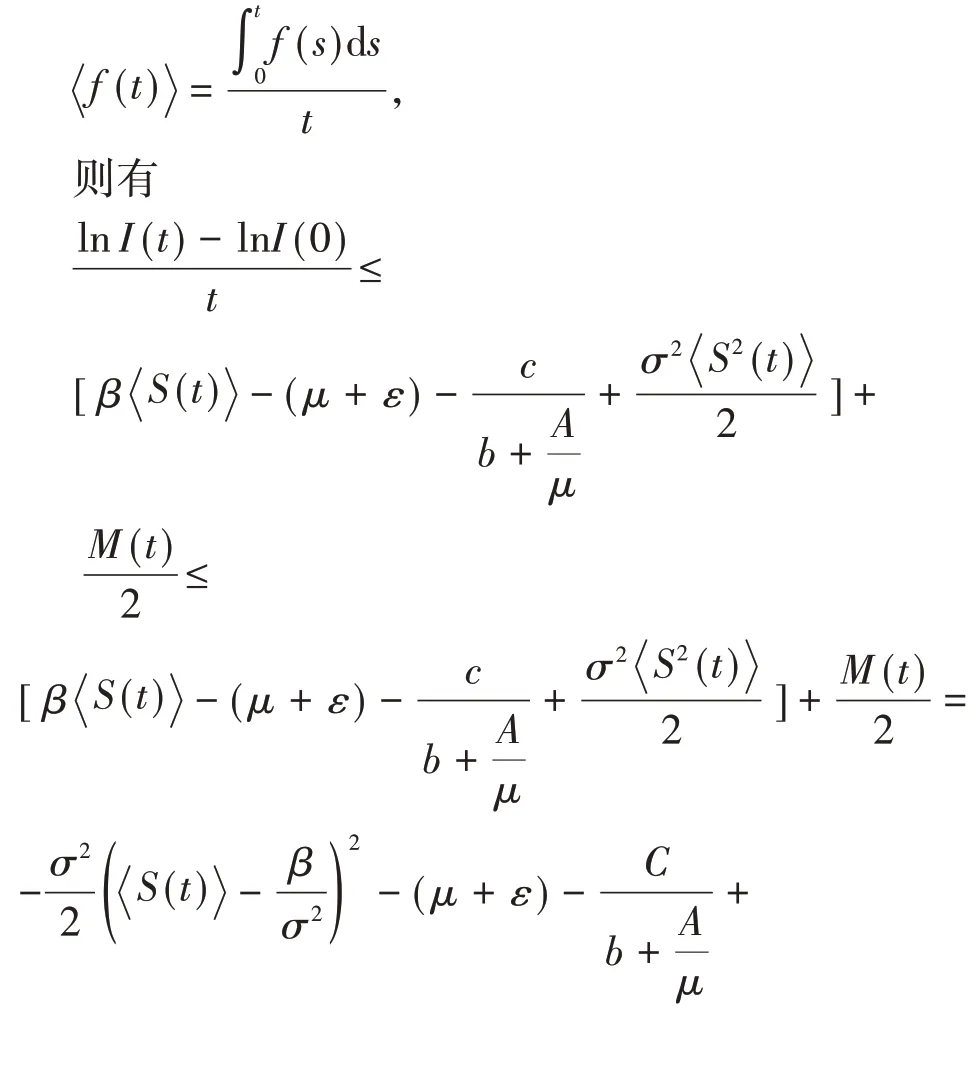
由强大数定律得

取(9)式两边的上极限，再将(10)式代入得

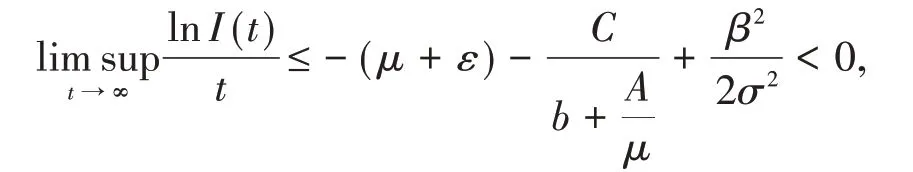
这意味着

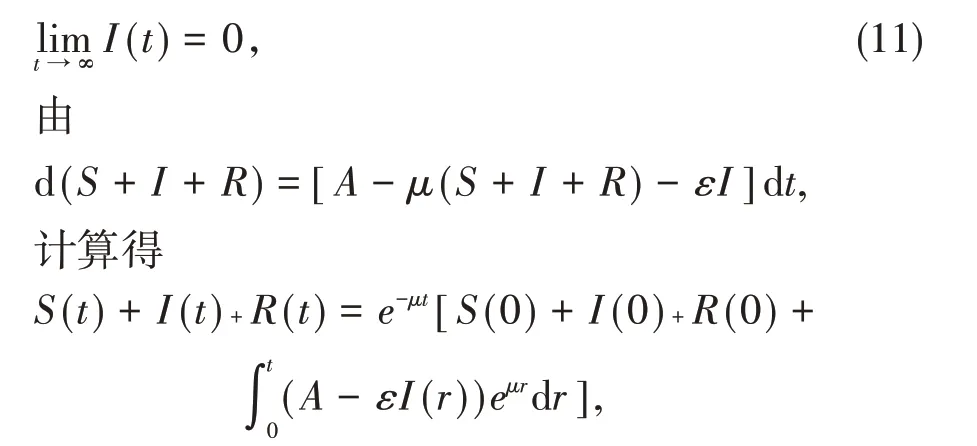
由洛必达法则及(11)式，得

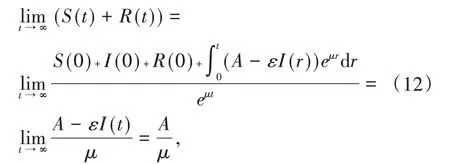
系统(2)中的第三项是

由此证明了定理2。

3 结语

在文献[7]模型的基础上，讨论了一类具有饱和恢复率的随机传染病模型，利用Lyapunov 泛函方法讨论了模型正解的存在性及唯一性及正不变集的存在性，并使用Itô 公式及强大数定律得到了染病群体及治愈者群体灭绝的充分性条件。定理2表明，如果白噪声强度满足一定条件，能够保证足够大，则I(t)、R(t)几乎必然指数趋于0，即疾病将将消失。这说明较大的随机扰动会对传染病模型中的各类群体产生影响，具有重要的实际意义。