幂级数和函数的求法及应用

孟献青

(1.山西大同大学数学与统计学院，山西大同 037009;2.山西大同大学量子信息科学研究所，山西大同，037009）

幂级数求和函数是级数部分的重点和难点，幂级数的和函数在求数列极限、数项级数求和、不等式的证明、近似计算等方面都有着非常广泛的应用。虽然幂级数求和函数，主要是利用和函数的性质，通过四则运算、逐项可导和逐项积分，转化为常见的已知和函数的幂级数进行求解。但在学习过程中，部分同学遇到具体问题却不知从何下手。着重讨论了教学过程中遇到的三类幂级数的求和问题，并介绍了幂级数和函数的应用。文中假定以下所有操作均在幂级数的收敛区间内进行。

1 常用结论

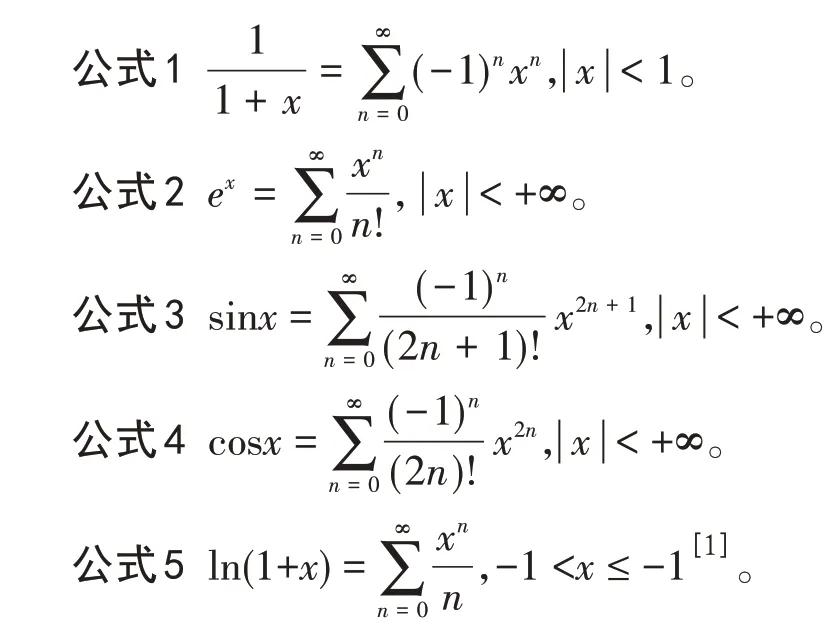
2 主要内容

2.1 p(n)在分子上

例1求下列幂级数的和函数。

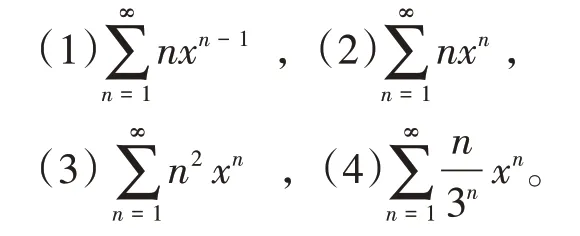
解（1）与等比级数相比，需要消掉系数n，因为(xn)′=nxn-1，所以可以把nxn-1先替换成(xn)′，再根据幂级数和函数的性质，先求等比级数的和，再求导进行计算。

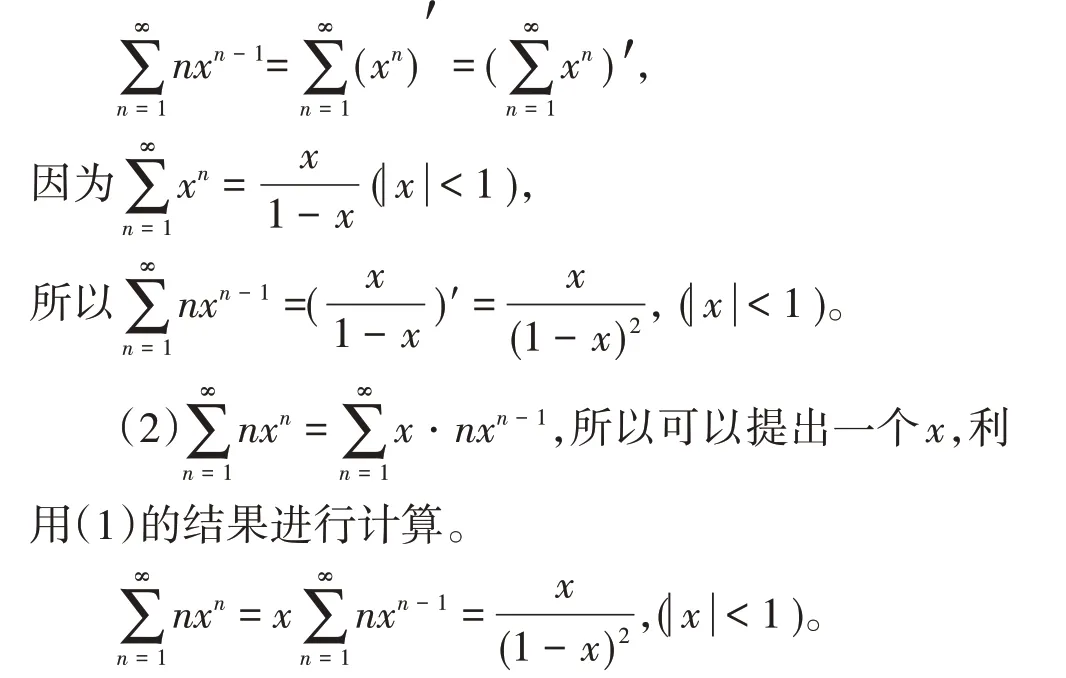
（3）难点是n2，不能直接利用上面的方法，但是可以把系数做相应的变形，从而把级数转换成熟悉的类型进行求解。

2.2 p(n)在分母上

例2求下列幂级数的和函数。

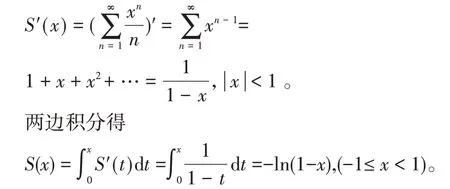
（2）分母是n，分子的幂次是n+1，xn+1直接求导不能约去n，故可以先提出一个x，使分母和分子的幂次相同，然后再逐项求导，转化成（1）的类型计算。

（3）分母是n+1，分子的幂次是n，xn直接求导不能约去n+1，故可以先乘x，使分母和分子的幂次都为n+1，然后再逐项求导，转化成熟悉的类型进行计算。

（4）因为(xn+1)″=n(n+1)xn-1，所以先把分子的幂次变成n+1，通过两次求导可以约去系数，然后转换成公比是-x的等比级数进行计算。

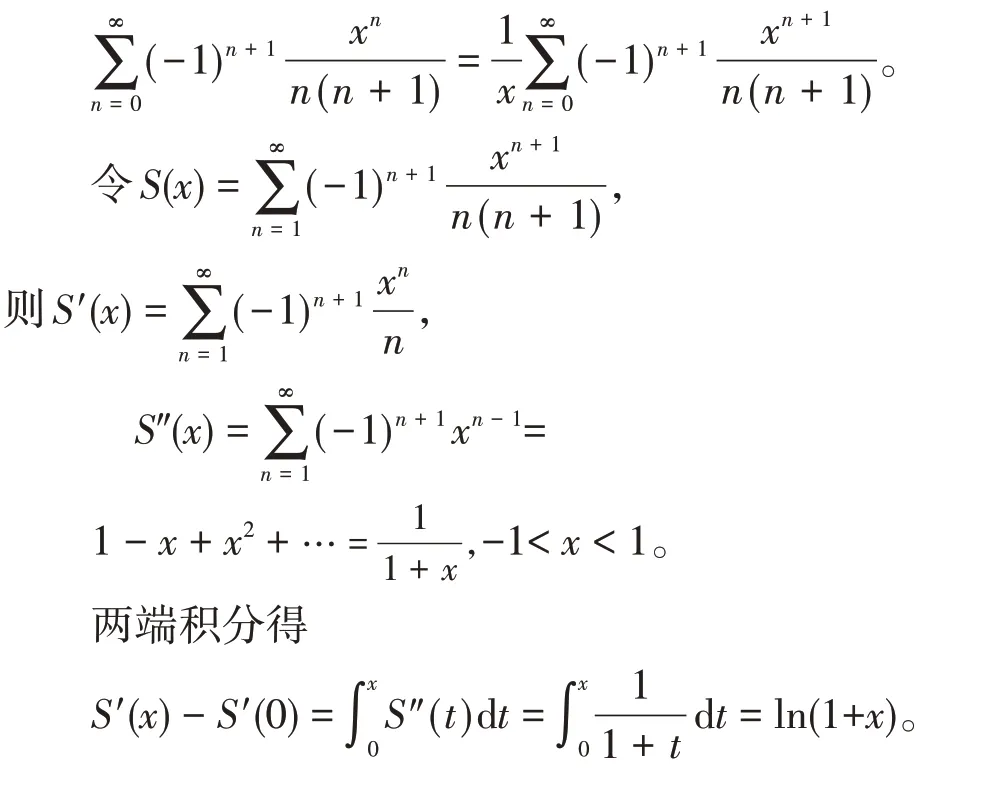
因为S′(0)=0，

所以S′(x)=ln(1+x)。

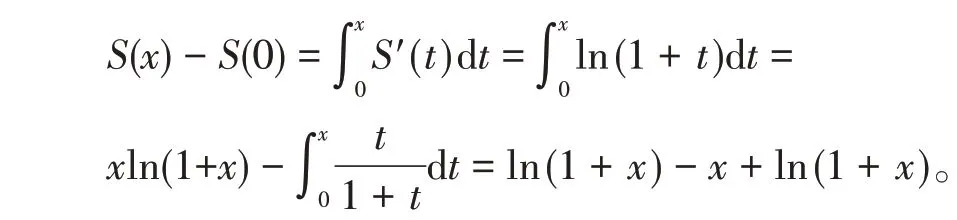
因为S(0)=0，

所以S(x)=(1+x)ln(1+x)-x，(-1＜x≤1)。

2.3 p(n)中含有阶乘

例3求下列幂级数的和函数。

解（1）由于该级数的分母中含有阶乘，与ex的麦克劳林展开式比较相似，所以做适当的变形，利用公式2进行求和。

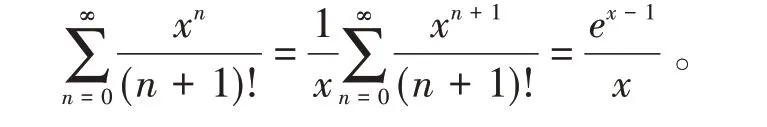
（2）该级数的系数与正弦级数的麦克劳林展开式比较相似，但是分子上又包含n+1，所以难点是如何消去n+1，然后结合正弦函数的展开式进行计算。

幂级数求和函数常用的方法就是逐项求导和逐项积分，通过一些简单的运算，把所求幂级数转化为已知函数的幂级数展开式进行求解。常用的解题思路是：如果幂级数的系数是n的有理整式或有理分式，可将该级数转化为这两种基本类型进行求解，主要利用的是等比级数求和。如果一般项分母中含有阶乘，则可向ex,sinx,cosx的麦克劳林展开式转化，从而得到新级数的和函数，再经过转化便可得到原级数的和函数。

3 幂级数和函数的应用

3.1 求数项级数的和

数项级数求和是高等数学常见的一类题型，在高等数学竞赛中和全国硕士研究生统一考试中频频出现。对于这种题型，通过观察级数一般项的特征，构造幂级数，然后转化为计算幂级数的和函数，再代入特殊值进行计算。

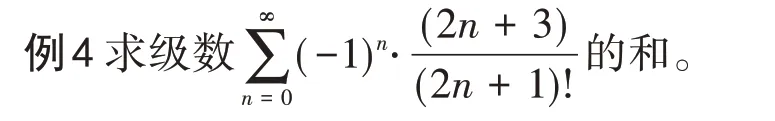
解观察到级数的分母中含有(2n+1)!，不难猜测其求解过程与sinx或cosx的幂级数展开式有关，所以构造幂级数，当x=1 时即为所求。令

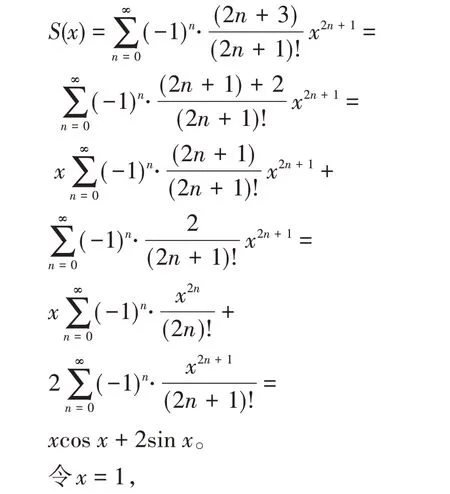
则原式=S(1)=cos1+2sin1。

3.2 求数列的极限

极限是高等数学的基础，它的计算灵活多样，技巧性强，且各有优点，用幂级数的和函数求极限是一种很重要的方法[3]。

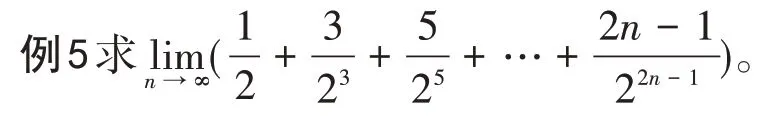
解构造幂级数时，即为所求。该级数的收敛半径为R=1，先求幂级数的和函数。

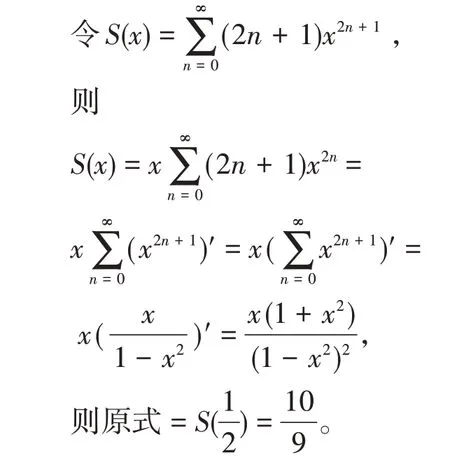
3.3 求积分

积分的计算在高等数学中有着非常重要的作用，积分计算的技巧性特别强，积分常用的方法是换元法和分部积分法，然而对于某些积分，利用幂级数的和函数求解，会使求解变得特别简单快捷[3]。

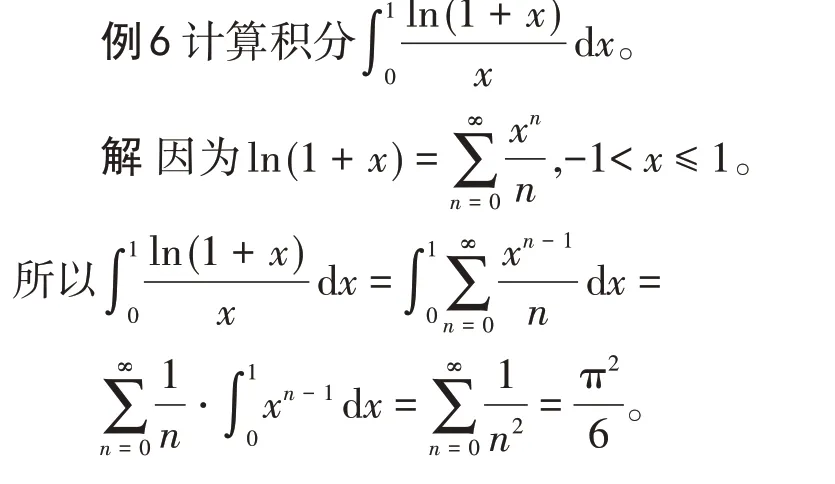
4 结语

介绍了常见的三种类型的幂级数求和函数的方法，并列举了幂级数和函数的一些应用。在计算和函数时，需要进行一些巧妙的处理，利用四则运算拆分成熟悉的幂级数求和，或者利用幂级数的性质进行逐项求导或逐项积分，转化成熟悉的类型进行求解。利用幂级数的和函数求解数项级数的和是历年考试的一个重点，形式灵活多变。所以在高等数学的学习中，一定要多角度思考问题，做到融汇贯通，把各个知识点有机的结合起来，不断探索新的、快捷的解题方法。