刚性圆环平面运动的力学分析

高彩云，刘 越

（1.山西大同大学物理与电子科学学院，山西大同 037009；2.山西大学理论物理研究所，山西太原 030006）

日常生活中乒乓球、足球、篮球等在桌子上或地板上滚动，各种轮子在道路上滚动等现象，不仅显现出丰富的运动图像[1-3]，而且经常作为力学问题进行研究[4-6]。物体的形状和运动的初始条件，以及圆形物体运动时与地面间的相互作用可以导致复杂的、有时甚至是不可预测的结果。例如，乒乓球放在桌子上，按动其背面，球开始滚动并向前滑动一定距离之后又返回；在体操比赛中，吊环被扔出后会回到运动员手中。文章以刚性圆环（简称圆环）为例研究圆形物体(球形、环形)在水平面上的运动。

1 刚性圆环模型假设

假设均质刚性圆环的质量为m，半径为r，质心速度为vc，角速度为ω，圆环与地面接触的点（着地点）P的速度为vp，简化模型如图1所示。

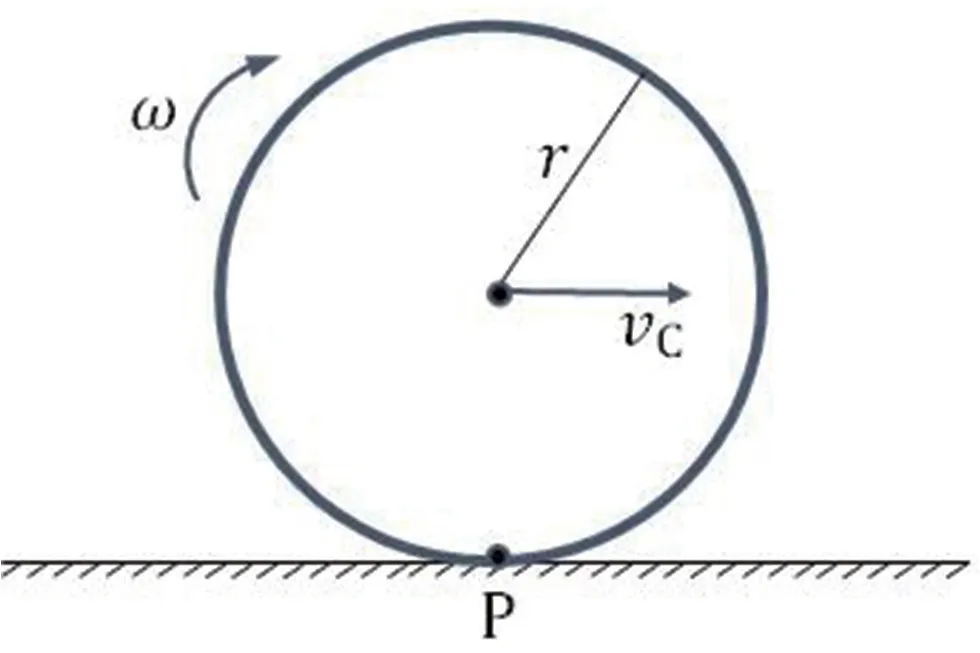
图1 圆环水平面滚动简化模型

根据上述假设，刚性圆环在水平面上平行运动，在竖直方向，向下的重力与向上的支持力，这两个力是平衡的；在水平方向，地面施加的摩擦力是静摩擦力或滑动摩擦力，由圆环与地面相对地面的接触点（着地点）P 点的速度决定，如果接触点速度为零，则水平力为静摩擦力；如果不为零，则水平力是滑动摩擦力。根据圆环运动的初始条件，可以确定着地点P相对于地面的速度vp，圆环对质心的转动惯量和地面粗糙程度决定了vp是怎么随时间变化的，从而决定了圆环运动特征的变化情况[7]。着地点P相对于地面的速度vp是质心速度和围绕质心速度的叠加[8]，所以需要更详细地讨论。

2 刚性圆环运动分析

设圆环质心初速度为vc0，初始角速度为ω0，着地点随圆环旋转线速度为vc0，则vp0=ω0r。

2.1 当vc0与vp0反向时圆环运动分析

1)vc0=ω0r

初始状态vc0与vp0是方向相反，矢量之和为零，圆环着地点P 点相对于地面速率0，即圆环进行滚动运动而不滑动。在水平方向，环受到静摩擦力，其大小在0～fmax范围内，fmax≈μN，方向与环P 的运动方向相反。下面用反论证法分析下一时刻环在水平方向上的摩擦力，分析此时环受到地面的摩擦力是静摩擦力还是滑动摩擦力[9]。若摩擦力f的方向向右，则vc变大、ω变小，而此时圆环与地面接触点P的速度vp大小不为0，而且方向是向右的，因此可以推断此时水平方向摩擦力的方向应向左，这个结果与假设是矛盾的；若摩擦力f的方向向左，则vc变小、ω变大，而此时圆环与地面接触点P 的速度vp大小不为0，而且方向是向左的，因此可以推断此时水平方向摩擦力的方向应该向右，这个结果与假设也是矛盾的。由以上的分析可以得到，在vc0与vp0相反方向且矢量和为0 的初始条件下，圆环在水平方向上受到的摩擦力为0。

因此可以得到结论：在圆环与地面接触点P的速度vp为0 之后，圆环在水平方向上受到地面的摩擦力为0，而且圆环作的是质心运动速度vc0和旋转角速度ω0都保持不变的运动，也就是没有滑动只有滚动的无滑滚动，可以将这种无滑滚动认为是保持稳定的平衡状态。

2)vc0＜ω0r

当vc0与vp0反向且vc0＜ω0r时，在初始时刻的下一时刻，圆环着地点P 的速度的方向就会向左，且与质心速度vc反向，着地点P 点和圆环整体都会受到方向向右的滑动摩擦力f=μmg，f会使vc增大、ω减小和vp减小。由刚体运动的质心定理和质心转动定理[6]可以得到:

由此可得着地点速率：

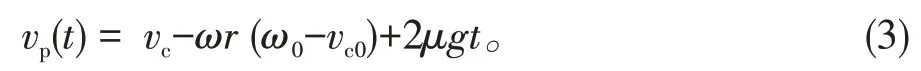
如果质心速度vc为正，则表示环正向运动。如果质心速度vc为负，则表示环向相反方向运动。正转速ω表示环绕中心正方向旋转，负转速意味着环绕中心负方向旋转，当P 点速度vp为正时，意味着环上的摩擦力是滑动摩擦力，当P 点速度减小到0 时，环上的摩擦力变为静摩擦力。

分别令着地点速度的大小vp、质心速度的大小vc和旋转角速度ω为0，得到了3 个时刻t1、t′1和t″1，t1=(ω0r-vc0)，t′1在这种情况下不存在，t″1=ω0r/μg。公式(1)～(3)适用的时间段为t∈[0，t1]。根据(1)～(3)式，在t∈[0，t1]时间段内，质心速率vc不断的增加而着地点的速率不断的减小最终会减小到0，旋转角速度ω不断的减小。直到t=t1时，vp(t)=0，在t1之后，圆环会保持无滑滚动的平衡状态不变。总之，在这种条件下圆环移动的方向不发生变化、运动速度随时间增加，增大到一定时刻不改变，旋转方向不改变，旋转速度随时间降低，在满足要求vp(t)=vc-ωr=0之后，旋转速度也不再变化。

在vc0与vp0反向且v0＜ω0r时，圆环作滚动减慢，移动加快的运动，它会一直向前运动，不会作回滚运动，最终达到无滑滚动的平衡状态。

3)vc0＞ω0r

当vc0与vp0反向且vc0＞ω0r时，在初始时刻的下一时刻，圆环着地点P 的速度vp的方向会与质心速度vc同向，即向右。所以着地点P 点会受到向左的滑动摩擦力f=μmg，f会使vc减小、ω增大和vp减小，可以得到：

由此可得着地点速率：

分别令着地点速度的大小vp、质心速度的大小vc和旋转角速度ω分别为0，得到了3个时刻、和t2、t′2和t″2，t2=(vc0-ωr)/2μgt，t′2=vc0/μg,t″2在这种情况下不存在。公式(4)～(6)适用的时间段为t∈[0,t2]。根据(4)～(6)式，在时间段内，质心的速率vc不断减小但没有减小到0，着地点速率vp不断减小且减小到0，旋转角速度不断增大。直到t=t2时，vp(t)=0；在t2之后，圆环会保持无滑滚动的平衡状态不变。因此，在t2时刻圆环的移动的方向不发生变化、运动速率减小直到一定时刻不改变，旋转方向不改变、旋转速度增加，在满足要求vp(t)=vc-ωr=0 后，旋转速度也不再变化。

在vc0与vp0反向且vc0＞ω0r 时，圆环作滚动加快，移动减慢的运动，它会一直向前运动，不会作回滚运动，最终达到无滑滚动的平衡状态。

2.2 当vc0与vp0同向时圆环运动分析

当初始条件为vc0与vp0同向时，环在开始时刻处于打滑状态。这里允许与可以分别为0则，对应两个速度特例，即在圆环运动开始的时候只有转动没有平动或只有平动没有转动。圆环着地点初始速度方向水平向右，受到地面的摩擦力应该是滑动摩擦力，大小为f=μN=μmg、方向水平向左。可以得到：

由此可得着地点P在任一时刻速率：

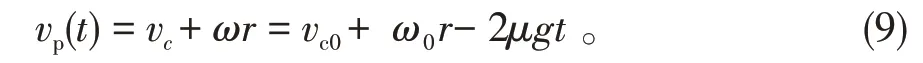
分别令着地点速率vp、质心速率vc和旋转角速度ω分别为0，得到了3 个时刻t3、t′3、t″3，t3=(vc0+ωr)/2μg，t′3=vc0/μg，t″3=ω0r/μg。(7)～(9) 式是在着地点P 的速度vp方向向右，滑动摩擦力向左条件下得到的，所以适用的时间段为t∈[0,t3]。根据(7)～(9)式，在t∈[0,t3]时间段内，质心速率vc、旋转角速度ω和着地点速率vp都会不断增大；在t=t3时，vp(t)=0；在t3之后，圆环会保持无滑滚动的平衡状态不变。在vc0与vp0同向的初始条件下，圆环的运动会存在两种情形。

1)vc0＜ω0r

如果vc0与vp0同向且vc0＜ω0r时，根据圆环的运动情况可知：t′3＜t3＜t″3，在t=t3时，vc(t3)=(vc0-ω0r)/2 ＜0，ω(t3)=(vc0-ω0r)/2 ＞0。在t∈[0,t3]时间段内，圆环质心的运动方向没有发生变化，但是运动的速度不断减小直到减小到0为止；圆环的转动方向也没有发生改变，转动速度随时间减小但没有减小到0。在t∈[t′3,t3]时间段内，圆环出现反向运动（即圆环回滚现象），圆环反向加速运动，转动速度仍然减小，但转动的方向依旧不变。直到着地点vp的速度为0，也就是到了t3时刻，摩擦力变为了静摩擦力。在t3时刻之后，圆环会保持无滑滚动的平衡状态不变。圆环在t∈[0,t′3]内质心移动的最大距离为：

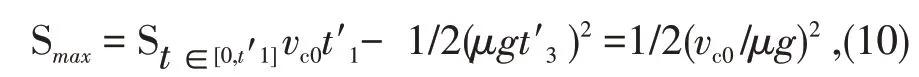
式中，距离公式中的平方项表示此距离与质心的初速度和圆环与地面的摩擦系数密切相关。

总之，当初始条件为vc0与vp0同向且vc0＜ω0r时，圆环质心移动的方向会改变，出现圆环回滚现象，移动的速度会不断减小，减小到0之后反向加速且速度增大到一定时刻不在发生变化；圆环的转动方向不发生变化，转动的速度会不断变小，最终达到稳定状态。

因此，当vc0与vp0同向vc0＜ω0r且时，圆环作滚动减慢，移动先变慢然后反向加速的运动，它会出现回滚现象，最终达到无滑滚动的平衡状态。

2)vc0＞ω0r

如果vc0与vp0同向且vc0＞ω0r时，根据圆环的运动情况可知t′3＜t3＜t″3；在t=t3时刻，vc(t3)=(vc0-ω0r)/2 ＜0，ω(t3)=(vc0-ω0r)/2 ＞0。在t∈[0,t″3]时间段内，圆环质心运动的速度减小但没有减小到0，运动的方向没有发生改变；圆环转动的方向不变，转动的速度不断减小直到减小到0 为止。在t∈[t″3,t3]时间段内，圆环质心运动的方向继续不变，运动的速度也继续减小；圆环转动的方向发生变化，与原来反向，转动的速度随时间增大。在t3时刻之后，圆环会保持无滑滚动的平衡状态不变。

总之，当初始条件为vc0与vp0同向且vc0＞ω0r时，圆环质心移动的方向保持不变，移动的速度不断减小，减小到一定时刻不再改变；圆环转动的方向会改变，转动的速度先随时间减小，减小到0之后，反向加速转动加速到一定时刻不再发生改变。因此，当vc0与vp0同向且vc0＞ω0r时，圆环作移动减慢，滚动先减慢然后反向加速的运动，它会一直向前运动，不会作回滚运动，最终达到无滑滚动的平衡状态。

3 结语

圆环的初始运动情形对于分析圆环的回滚运动具有重要意义。当vc0与vp0反向且vc0=ω0r时，圆环不受到地面摩擦力的作用，在圆环与地面接触点P的速度为0之后，圆环作质心速度和旋转角速度不变的运动，也就是保持平衡状态；当vc0与vp0反向且vc0＜ω0r时，地面的滑动摩擦力作用于圆环，圆环会继续保持前行，滚动减慢，平动加快，最后达到平衡状态；当vc0与vp0反向且vc0＞ω0r时，地面的滑动摩擦力也作用于圆环，圆环会继续保持前行，滚动加快，平动减慢，最后达到平衡状态。故在vc0与vp0反向时，圆环没有出现回滚现象；当vc0与vp0同向且vc0＜ω0r时，地面的滑动摩擦力作用于圆环，圆环会继续保持前行，滚动减慢，平动加快，最后达到平衡状态；当vc0与vp0同向且vc0＞ω0r时，地面的滑动摩擦力作用于圆环，圆环会前行一段后反向加速，滚动减慢，最后达到平衡状态。