基于投影寻踪的中国省际高质量发展实例研究

吴思翰，楼文高，2

（1.上海理工大学 光电信息与计算机工程学院，上海 200093；2.上海商学院 校长办公室，上海 200235）

0 引言

改革开放至中共十八大之前，中国经济一直保持着较高速增长态势。但是在高投入、高消耗和高增长的背景下，能源过度消耗、环境质量下降、经济发展不均衡以及创新驱动不足等问题越来越明显［1］。为了解决上述问题，中共十八届五中全会提出了五大发展理念，并且在十九大报告中指出“我国经济已由高速增长阶段转向高质量发展阶段”，说明中国经济步入质量为首的新篇章，高质量发展成为中国当前以及未来经济建设的核心［2］。

大多数学者对高质量发展的研究主要包括基本内涵、评价体系和水平测度3 个方面。师博等［1］采用均等权重赋值法评价了中国东部、中部以及西部地区的经济增长质量；Frolov 等［3］基于矩阵方法，结合年均生产率增长率和人均发展指数构建区域经济增长质量评价体系；刘干等［4］从居民生活水平、产业结构等5 个方面构建经济高质量发展评价指标体系，通过模糊综合评价法和熵值法进行实证研究；周吉等［5］采用主成分分析法（PCA）对江西省经济高质量发展水平进行实证研究；马茹等［6］采用线性加权法对区域经济高质量发展水平进行综合评价研究；魏敏等［7］采用熵权TOPSIS 法对我国经济高质量发展水平及其空间分布规律进行实证研究。

上述研究中采用的评价方法都存在局限性；如采用均等权重法对权重赋值，令增长基本面（α）和社会成果（β）的权重均为0.5，但通过研究发现，经济高质量发展过程中社会成果的权重要大于增长基本面的权重，故均等权重法赋值并不合理；主成分分析法要求样本数量相对较多，至少是指标数的3～5 倍以上，否则结果不稳定；TOPSIS 法属于逼近理想解的综合评价方法，需要采用变异系数法、信息熵等方法事先确定指标权重，而这本身就是经济高质量发展综合评价的关键内容之一。传统的统计方法主要适用于正态分布的数据，对于处理非正态分布的数据可能会出现无法合理解释的结果或者结果的可靠性和有效性难以保证。综上所述，高质量经济发展综合评价仍然是一个需要深入研究的问题。

同时，由Friedman 等［8］提出的非线性、高维、非正态分布数据建模的投影寻踪分类（PPC）模型已广泛应用于各种研究领域，并取得较好效果，如于晓虹等［9］采用PPC 模型对省际普惠金融发展水平进行综合评价、排序和分类；虞玉华等［10］运用PPC 模型对体育期刊学术水平进行综合评价与研究；郭倩等［11］运用PPC 模型对水资源承载力进行综合评价并分析其投影特征值的历年变化特征；Liu 等［12］运用PPC 模型对区域地表水环境进行评价。因此，本文基于高质量发展理念及PPC 模型原理，建立相应的评价指标体系，通过PPC 模型对中国30 个省市2015-2018 年的高质量发展水平进行综合评价、排序和分类，并且与采用PCA 法、TOPSIS 法的评价结果进行对比，结果表明PPC 模型更加合理有效。

1 高质量发展水平评价指标体系建立

1.1 评价指标体系构建

梳理有关文献发现，不同学者从自身知识结构及对高质量发展内涵的不同理解，建立了相应的评价指标体系。师博等［1］构建了由6 个子系统组成的省际经济高质量发展指标体系；魏敏等［7］则构建了包括经济结构优化、创新驱动发展等10 个子系统53 个测度指标的测度体系；王竹君等［13］通过福利变化与成果分配、生态环境保护以及居民经济素质3 个方面7 个二级指标17 个三级指标，构建指标体系结构；刘丽波等［14］根据经济高质量发展内涵和不同阶段特征，构建了由动能转换、产业结构化、需求转型、投入产出效率以及优化发展环境5 个特征29 个指标组成的评价体系；詹新宇等［15］从创新、协调、绿色、开发、共享五大发展理念的角度构建了31 个三级指标的经济增长质量指标体系。综合以上学者建立的经济高质量发展评价指标体系，再从高质量发展内涵的角度出发，考虑到评价指标体系的实用性、可比性、获得数据的便捷性以及可操作性等原则，本文建立了由6 个方面、27 个指标构成的评价体系，具体指标及含义如表1 所示。

Table 1 High-quality development level evaluation index system表1 高质量发展水平评价指标体系

1.2 数据来源

由于港澳台地区和西藏自治区测度指标数据缺失较多，故只研究了其他具有完整数据的省市。所有数据均来源于2016-2019 年《中国统计年鉴》《中国科技统计年鉴》《中国能源统计年鉴》，个别数据采集于各省《国民经济和社会发展统计公报》和历年统计年鉴。

2 投影寻踪分类（PPC）模型建立

2.1 数据归一化处理

由于所收集到的部分数据值较大并且计算量复杂度较高，因而建模前要对样本数据进行归一化处理，公式为：Yij=(Xij-Xjmin)/(Xjmax-Xjmin)；对于样本数据的负向指标均进行正向化处理，公式为：Yij=(Xjmax-Xij)/(Xjmax-Xjmin)。其中，Xij和Yij分别表示原始指标值和归一化处理后的指标值，Xjmin为第j 个指标的最小值，Xjmax为最大值。

2.2 目标函数构造

投影寻踪就是将m维数据综合成以（a1，a2，…，am）为投影方向的投影特征值，如式（1）所示。

PPC 模型的最有效一维模型目标函数就是Sz与Dz乘积的最大化，即：

其中，Sz为zi的标准差，其值越大说明投影点在整体上越分散；Dz为其局部密度值，其值越大表示投影点局部越密集。Sz和Dz分别如式（4）、式（5）所示。

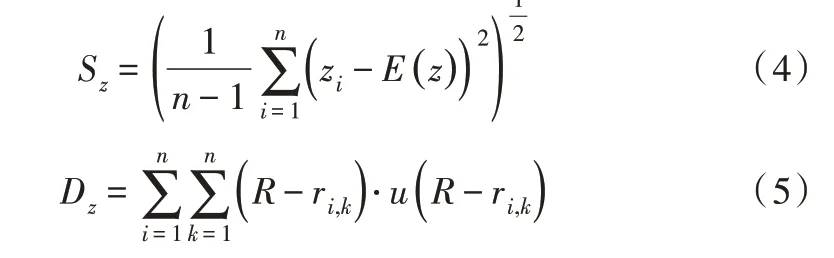
其中,E(z)为zi的平均值；ri,k为样本i与k距离差的绝对值；R为局部密度的窗口半径，最优化结果的参数取决于R值大小，从楼文高等［17］研究结果可知，R的合理取值范围应为max（ri,j）/5≤R≤max（ri,）j/3；u(R-ri,k)为单位阶跃函数，如果u(R-ri,k)>0，则其值为1，否则为0。

由于式（3）是以aj为变量的高维复杂非线性优化问题，因而采用群搜索算法（GSO）［18-19］对式（3）中的最佳投影向量a→及其系数aj（权重）进行优化求解。根据楼文高等［17］提出的定理1 求得全局最优解。根据最终求得的指标权重对其重要性进行排序，同时根据各样本投影值的大小进行分类排序。

2.3 群搜索算法

群搜索算法（GSO）是由发现者、加入者和游荡者模型所产生的算法。在每次迭代中，当前最优个体为发现者，它会根据自身位置向周围寻找更好的位置。其他个体按比例分为加入者和游荡者，加入者在跟随发现者的同时进行搜索，游荡者则朝任意方向随机移动。本文将采用张雯雰等［18］提出的带趋势预测的GSO 算法求解上述式（3），算法简述如下：

在n维空间中，第i个成员在第k次迭代时的位置为，经验为。在迭代开始之前，成员的位置随机分布，经验值为0。

在k次迭代时，将位置最好的成员设为发现者，记作。当时，随机选取成员的20%以（6）式为基准进行经验积累，再通过式（7）预测位置。

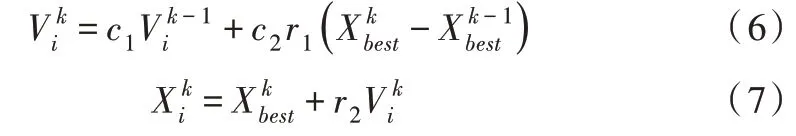
其中，r1和r2为（0，1）内的均匀随机数，c1和c2为常量系数。再随机选择剩余成员的70%随机选择加入者，加入者通过一个随机步长靠近发现者如式（8）所示。

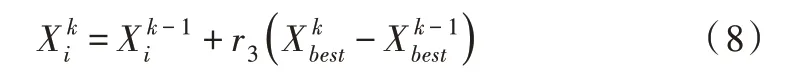
其中，r3为（0，1）内的均匀随机数。剩余成员作为游荡者向任意方向随机游荡，如式（9）所示。

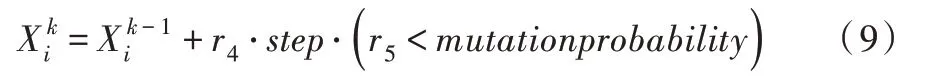
其中,r4和r5为（0，1）内的均匀随机数；step为步长常量；mutationprobability为分量变异概率，其值为，迭代次数越多，值越小。“<”运算是衡量算式左右两边的大小，返回值为布尔值，用0、1 表示。

3 省际高质量发展水平综合评价的PPC 实证研究

3.1 数据归一化预处理结果

在27 个指标中，x15、x20、x21、x22、x25以及x26均为负向指标，故采用负向指标的归一化方式处理，其他指标采用正向指标的归一化方式处理。数据的直方图分布表明，几乎所有指标的数据都不服从正态分布规律。

3.2 实证研究

将归一化后的数据导入GSO 投影寻踪程序中，令窗口半径R=max（ri,j）/5，根据上述定理，求得真正的全局最优解，其中投影值标准差Sz=0.761 3，局部密度Dz=295.094，目标函数Q(a)=224.661，窗口半径R=0.735 7，其中各评价指标的最佳投影向量系数（权重）aj=（0.322 2，0.254 9，0.252 8，0.299 6，0.131 8，0.210 4，0.267 8，0.131 5，0.022 3，0.159 1，0.234 9，0.209 7，0.246 2，0.186 6，0.109 6，0.070 4，0.243 0，0.154 2，0.192 8，0.204 0，0.056 8，0.185 1，0.249 9，0.045 6，0.098 5，0.188 1，0.013 8）。最后得到30个省的PPC 投影值以及排名结果如表2 所示。

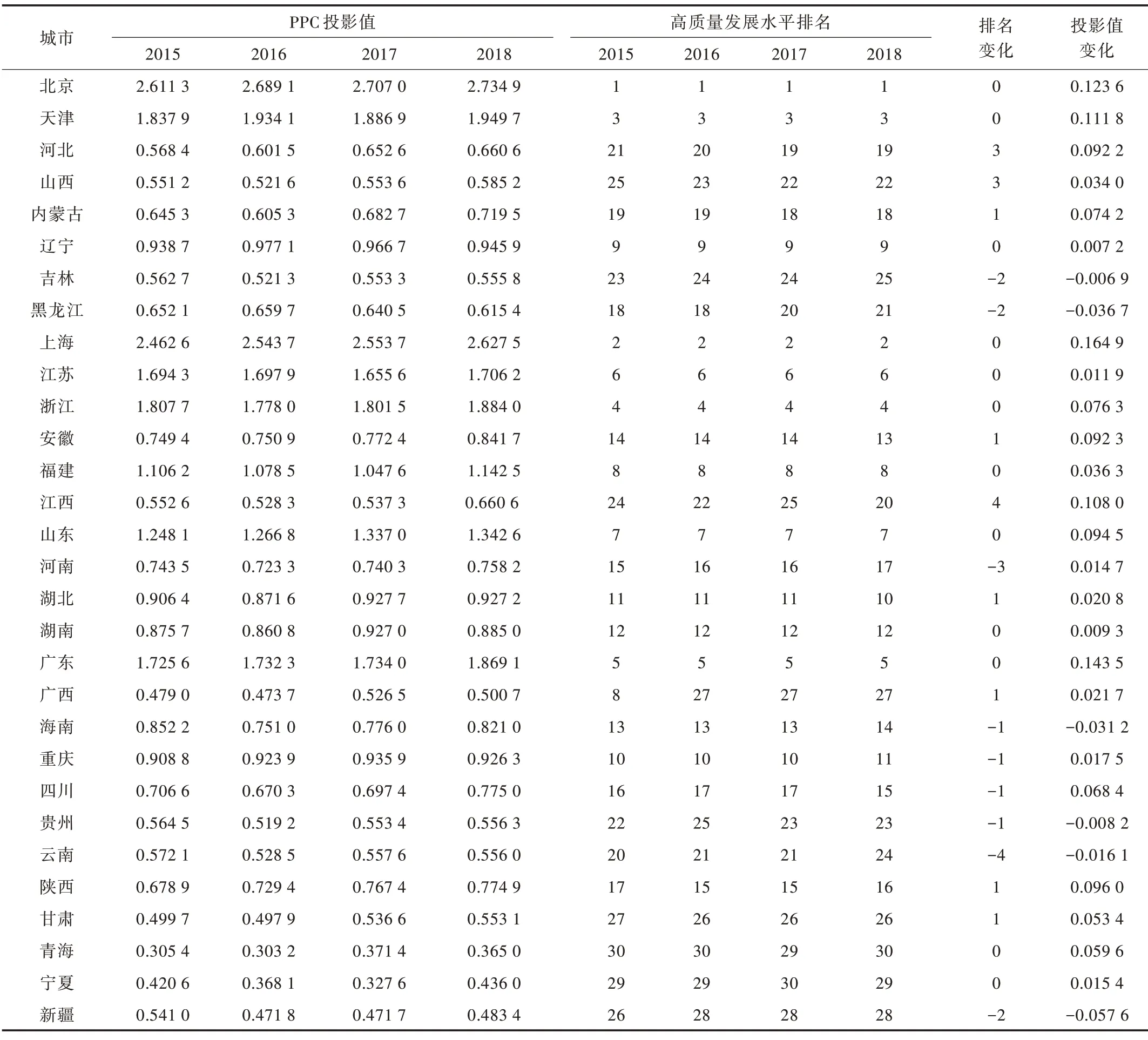
Table 2 30 provinces and cities’high-quality development level PPC projection value and its ranking in China during 2015-2018表2 2015-2018 年我国30 个省市高质量发展水平PPC 投影值及其排名

3.3 结果探讨

3.3.1 评价指标特性解析

PPC 投影值与各指标之间呈线性关系，权重越大的指标对高质量发展水平的影响越明显。将这些评价指标的最佳投影向量系数从大到小排序为x1、x4、x7、x2、x3、x23、x13、x17、x11、x6、x12、x20、x19、x26、x14、x22、x10、x18、x5、x8、x15、x25、x16、x21、x24、x9、x27。在该评价指标体系中通过6 个方面权衡高质量发展水平，权重占比依次为23.82%、15.64%、13.20%、18.05%、16.72%、12.57%，可以看出，每个方面所占权重比较平均，尽管创新驱动发展指标不是最多，但其权重占总权重的比例最大，说明发展创新驱动是决定省际高质量发展水平高低的最重要特征，应该优先得到保证并且要高度重视。因此，要提升各省市高质量发展水平，必须改进权重大的指标（如R&D 人员投入力度等），这样才能取得事半功倍的效果。

3.3.2 省际高质量发展水平分类排序

由于PPC 模型所求得的投影值均为一维实数，因而既可以区分出各省市类型，又可以对同一类型的不同省市进行详细的排序研究。根据表2 历年排名情况，本文将30 个省市按2017 年高质量发展水平好坏分成三大类：第一类为超前型，包括北京和上海等6 个省市；第二类为中庸型，包括山东等15 个省市；第三类为落后型，包括山西等9 个省市。

4 权重及其排序结果比较

对于综合评价而言，确定合理的权重最为关键。本文采用基于变异系数法［20］、信息熵法［21］权重的TOPSIS 法和PCA 法［22］分别求得27 个指标数据的权重及其排序结果如表3 所示。采用PCA 法建模时，KMO 值等于0.458，小于0.5，说明该样本数据不太适合用PCA 进行综合评价。根据表4 可知，由于每个方法赋权重的原理不尽相同，因而最后求得的各方法权重及排名也会有所差异。其中，只有PPC方法的建模基本思想与人类开展综合评价、排序和分类研究的思维方式是一致的，又可适用于非线性、高维、非正态分布的数据分析，可以避免PCA 法要求数据近似正态分布、存在“维数祸根”等问题，同时不必像TOPSIS 法需要利用其他方法提前确定各指标权重。

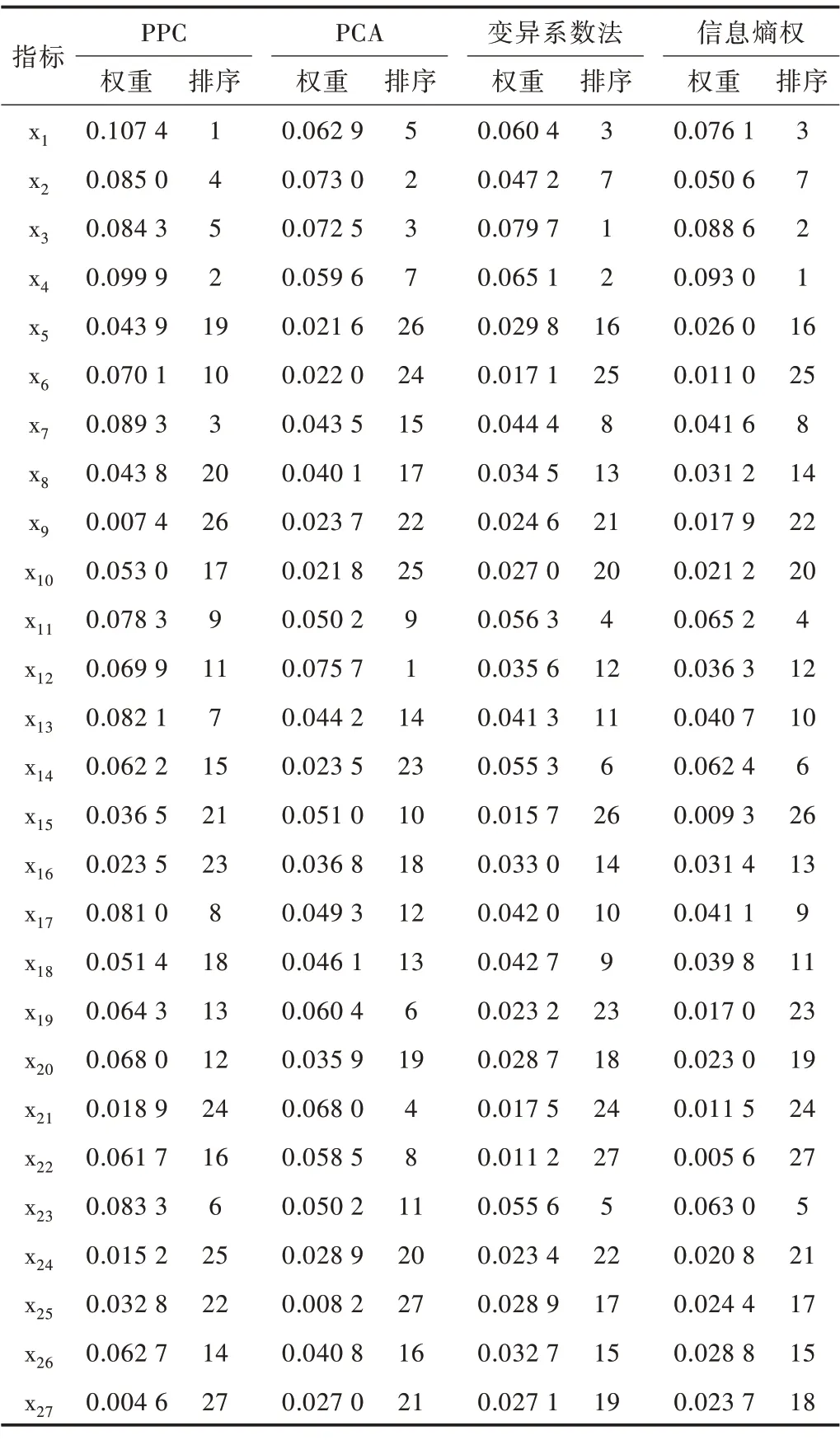
Table 3 Comparison of weights obtained by different evaluation methods and their ranking表3 不同评价方法得到的权重及其排序比较

5 结语

本文基于构建的中国省际高质量发展水平评价指标体系，采用以群搜索算法优化的PPC 模型对中国30 个省市进行高质量发展水平综合评价及排序分类研究。研究结果表明：①在本文研究的指标体系中，创新驱动发展对高质量发展水平影响最大，经济成果共享相对其他方面影响最小；②将30 个省市按投影值从高到低进行了排序并且将其分为三大类，北京等6 个省市为超前型，山东等15 个省市为平庸型，山西等9 个省市为落后型；③不同方法赋权重的原理不同，得到的权重值就会有所差异。可以根据权重值最大的指标，提出有利于提升各省市高质量发展水平的措施和建议；④相比于PCA 等其他方法，PPC 模型建模过程简洁，适用于分析高维、非正态的数据，为研究高质量发展水平提供一种更加科学、合理的新评价方法。