融合LSTM 预测需求的线型材料多批次优化下料方法

庞凯民，朱 波，张宏硕，刘 宁，张连富

（1.昆明理工大学 机电工程学院，云南 昆明 650500；2.沈阳机床（集团）有限责任公司，辽宁 沈阳 110142）

0 引言

线型材料在下料时只需考虑长度方向尺寸，属于一维下料范畴。开展一维优化下料研究，对提升线型材料利用率、降低生产成本具有重要意义［1-2］。一维优化下料问题在学术界已经研究多年，近年不断有优化算法提出，如黄秀玲等［3］采用蚁群算法和遗传混合模拟退火算法求解多规格一维型材优化下料问题；Pitombeiraneto 等［4］提出基于固定优化策略和随机局部搜索相结合算法。这些研究都聚焦在求解算法上，寻求一种有效的搜索算法，从巨大的下料解空间中搜索出近似最优解，由此获得更高的原材料利用率。与此同时，有些学者面向企业实际下料需求特性开展研究，从算法的优化运用角度提出提升原材料利用率的方法，集中式下料就是这样的一种典型方法。该方法通过将多个具有相似需求的下料任务（来自多个项目或者同行业的多个制造企业）进行整合，使得多个较小规模的下料问题融合为少数较大规模的下料问题，由此增加零件之间互补和契合的可能性，有利于获得更优的下料方案，从而提升原材料利用率，降低设备投入成本和开机成本。集中式下料研究有：张颖［5］将集中下料生产与实际钢材下料系统相结合，有效降低了下料成本；张洪等［6］针对某小批量产品在前期由于技术状态反复、工艺过程与材料消耗变更等问题，在优化工艺的同时引入集中下料思想，有效降低了产品成本。

为了更好满足客户的个性化需求，产品大规模定制、多批次、小批量生产成为制造企业的主要生产模式，该模式决定了制造企业下料具有如下特点：下料批次多、批次下料需求相似、单个批次下料规模不大、后续批次下料需求不明确等。针对这些下料特点，如果只针对每一批次进行优化而不考虑余料的使用（在本文中定义为批次下料）是难以获得较好的原材料总体利用率的。因此，有学者提出基于库存的下料，即将每次下料产生的余料进库存，每次下料优先使用库存余料，使余料能够得到有效利用。相关研究有：管卫利等［7］提出一种混合启发式下料算法，将库存余料参与到后续的下料过程；王婷婷等［8］提出一种运用动态规划与枚举结合的方法的优化下料算法，可有效降低生产成本。但是，由于后续批次下料需求未知，实质是被动利用余料，无法充分挖掘多次下料需求互补和契合的可能性。如果能对后续多个批次的下料需求进行准确预测，就可以按照集中式下料思想将多个批次的小规模下料任务整合成少数较大规模的下料任务，也即一次下料结合库存多余零件满足多次需求，从而实现更优的材料总体利用率。相对集中式下料对下料需求的横向整合，这是对下料需求的纵向整合，要解决的关键问题是对后续批次下料需求的准确预测。目前关于需求预测方法研究较多，其中深度学习模型之长短期记忆网络（LSTM）不仅能处理时间序列信息的延续性问题，还能应对长序列训练过程中的梯度消失和梯度爆炸问题，对解决预测问题具有显著优越性；王旭东等［9］提出一种基于LSTM 的单变量短期家庭电力需求预测模型，以此预测短期家庭的用电情况；林友芳等［10］提出一种基于LSTM 的出发地——目的地（OD）客运需求预测模型，通过显式建模客运需求时间序列内部的时间依赖关系和序列之间的空间依赖关系来预测未来一段时间所有OD 的客运需求量；李颖宏等［11］针对不同地域间出行的自流动性和关联性，提出基于LSTM 的共享单车需求预测模型，以此预测在不同时间段内共享单车的需求量；王晓飞等［12］基于Prophet-LSTM 模型，通过将PM2.5 日值浓度序列分解成趋势、周期和随机波动分量后，对随机波动分量建立LSTM 模型，以此对PM2.5 浓度进行预测。

本文提出一种融合下料需求预测的多批次线型材料优化下料方法。以LSTM 为预测工具对后续批次下料需求进行预测，根据预测结果按照集中式下料思想整合下料任务，通过经典的列生成法进行求解，并辅之以贪心算法补偿下料，解决预测误差导致的问题，最终实现原材料总体利用率最高目标。相比于传统的线型材料优化下料模型，本文提出的LSTM-CSP 模型从算法优化角度出发，对生产周期内后续零件需求量进行预测与集成，将多个较小规模的下料问题融合为少数较大规模的下料问题，保持需求量在不同批次间的关联。相比于传统的预测方法，LSTM 对于时间序列信息的预测精度更高。基于相关理论，本文构建了方法模型（LSTM-CSP），并将某制造企业型材下料的实际需求数据生成仿真数据集，开展仿真实验，验证了模型的有效性。

1 相关理论及方法

1.1 一维优化下料问题数学模型

一维优化下料问题原型可描述为：给定K种原材料，每种原材料长度和价格分别为Li、Vi，（i=1,2…K）；给定M种需要下料生成的零件，每种零件的长度为lj（j=1,2…M），di为第i种零件的需求量，设在满足所有零件的下料需求前提下如何使消耗的原材料总成本最小。构建数学模型如下：

其中，目标函数ZC是消耗原材料的价格总和；VK为第K种原材料价格；K为原材料种数；为采用第j种下料方式使用原材料K的数量；nK为第K种原材料的下料方案总数；di为第i种零件需求量；为使用第j种下料方式在第K种原材料上获得的第i种零件数量；为 第K种原材料上的一种可行的下料方式，通过求解一维背包问题得到，作为一个新的列参与到列生成法的迭代运算中。

1.2 列生成法

列生成法是一种求解大规模线性规划问题的解析算法，可有效降低变量的基变换次数，提升求解效率。优化下料是典型的NP 问题，列生成法将一维优化下料问题（主问题）限制到一个变量少、规模小的限制主问题（RMP）上，并对其进行求解［13-14］。所得解为RMP 的最优解而非主问题的最优解，因此需要通过一个子问题去检查是否存在未进基的变量使RMP 获得更好的解，即通过求解子问题来获取进基变量，并添加相应的列到RMP 中重新求解。当该变量存在时，将其添加到限制主问题中再次进行迭代求解；当不存在这样的变量时，即找到了问题的最优解。

主问题转化为限制主问题时，将一些变量强制限制为非基变量，通过子问题判断检验数σj=cj-cB B-1aj来找到进基的非基变量并将其列添加到RMP 中再次求解［15］。通过将RMP 转化为对应的对偶问题，可以进一步缩小RMP中的变量［16］，更方便得到cB B-1。列生成法流程如图1 所示。

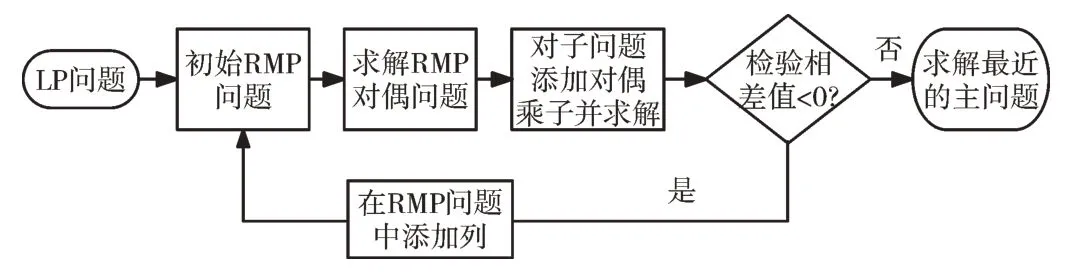
Fig.1 Flow of column generation method图1 列生成法流程

1.3 LSTM 神经网络

长短期记忆人工神经网络（LSTM）是一种改良的递归神经网络，不仅能有效处理时间序列信息的延续性问题［17］，还通过在隐藏层单元增添3 个信息控制单元有效解决了长序列训练过程中的梯度消失和梯度爆炸问题［18］。

当前时刻为t时，输出值h(t)不仅与输入x(t)有关，还与上一时刻的输出值h(t-1)有关。LSTM 的隐藏层单元A可将上一时刻输出状态h(t-1)传输给下一时刻，由上一时刻状态h(t-1)和当前输入x(t)共同决定当前输出状态h(t)。LSTM 在隐藏单元层内通过增加3 个控制单元（输入门，遗忘门，输出门）来控制整个细胞的活动状态，判断信息是否保留。输入门、遗忘门、输出门分别控制输入状态、输出状态和记忆细胞状态，由此完成对前一状态的更新［19］，其表达式如下：

实验组44例糖尿病患者中男26例,女18例,男女比例为13:9,患者年龄在35岁至79岁,平均年龄在(45.6±3.6)岁,平均病程在(2.3±0.5)月,其中有11例患者为Ⅰ型糖尿病患者,有33例患者为Ⅱ型糖尿病患者。对照组44例糖尿病患者中男27例,女17例,男女比例为27:17,患者年龄在39岁至77岁,平均年龄在(44.8±3.5)岁,平均病程在(2.2±0.4)月,其中有13例患者为Ⅰ型糖尿病患者,有31例患者为Ⅱ型糖尿病患。两组患者在年龄、性别比例、病程等一般资料上数据差异小(P>0.05)。

式中，W(t)为权重系数矩阵，i(t)的权重系数矩阵为Wix(t)，同理，b(t)为偏置矩阵，i(t)的偏置矩阵为bi(t)，σ为sigmoid函数，tan 为双曲正切函数，而状态信息C(t)、隐藏层输出h(t)和网络输出y(t)可表达为：

每个序列索引位置过程可归结为：更新遗忘门输出、更新输入门两部分输出、更新细胞状态、更新输出门输出、更新当前序列索引预测输出。LSTM 工作原理如图2 所示。

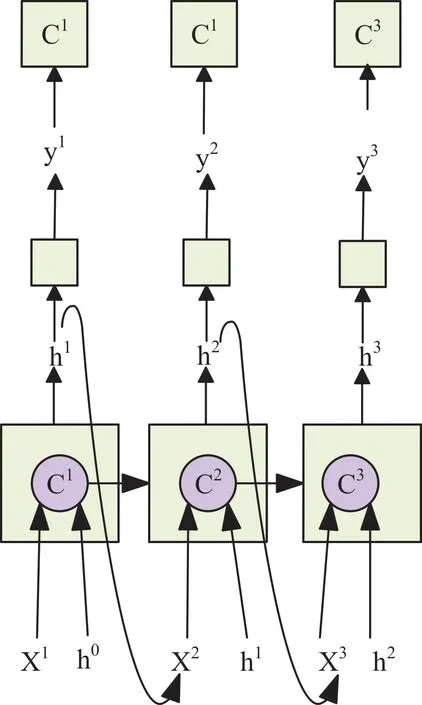
Fig.2 Overall flow of LSTM图2 LSTM 整体流程

2 多批次优化下料模型

融合LSTM 预测需求的线型材料多批次优化下料模型——LSTM-CSP 模型由3 个模块构成，分别为零件需求预测模块、优化下料模块和补偿下料模块，其工作流程如图3 所示。

零件需求预测模块对每种零件的历史需求量进行统计生成训练集，训练出长短期记忆网络（LSTM）来对未来一个主生产计划周期内（本文根据企业调研情况确定为7 天）的需求量进行预测，并将预测结果提供给后续的优化下料模块。该模块中，LSTM 根据其自身特点，通过控制门对数据进行流向控制，将序列信息（不同零件的需求量）进行循环并预测下一个批次中不同零件需求量。

优化下料模块汇总预测的各个批次零件需求，构建一维优化下料问题，并利用列生成法进行求解，求解步骤如下：①将各个零件的预测需求量集成；②将零件总体需求量作为约束带入优化下料模型；③采用启发式算法构造初始解；④将初始解带入到LSTM-CSP 模型中；⑤采用列生成法求解；⑥判断预测集成的零件需求量是否满足零件的实际需求量，若满足则退出优化下料模块；若不满足则转入补偿下料模块。

补偿下料模块用于解决零件需求预测存在误差和下料零件需求必须满足之间的矛盾。在下料过程中，首先在每种原材料上分别进行下料，得到一个初始的下料解，并将其加入到模型中，并采用列生成法进行迭代求解，从而得出最优下料方案。

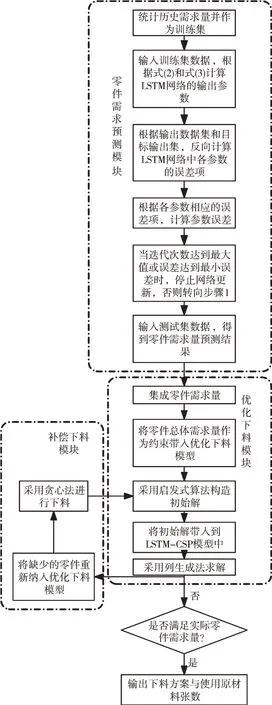
Fig.3 Flow of LSTM-CSP model图3 LSTM-CSP 模型流程

3 仿真实验

3.1 实验数据集

对某金属门窗企业的铝型材下料工序进行调研，获取其典型原材料和下料零件规格，如表1 所示。

对每种零件的实际需求量进行统计。每种零件收集到2 815条数据，其中，1-2 000条作为训练数据，2 001-2 808条作为测试数据，剩余的7 条作为零件实际需求量，数据如表2 所示。

3.2 实验结果与分析

3.2.1 零件需求预测性能实验

对需求的准确预测是本模型实现的核心，因此首先对模型的预测性能进行实验测试。在实验过程中发现LSTM-CSP 算法的预测窗口（即步长λ）对预测性能有影响。考虑到反向传播的有效性和训练的难度，通常以训练样本的一半作为基础步长设置。前期实验结果表明，λ=1 350时预测精度达到最高。为探究步长对模型预测精度的影响，本文分别选择λ=750，λ=1 350 和λ=1 900 时对LSTMCSP 算法进行对比实验。

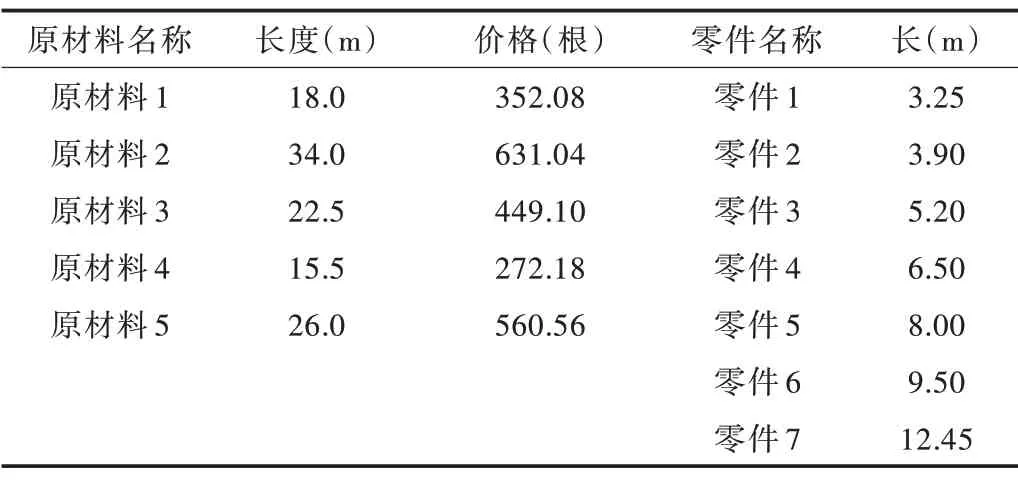
Table 1 Data of raw materials and parts表1 原材料与零件数据

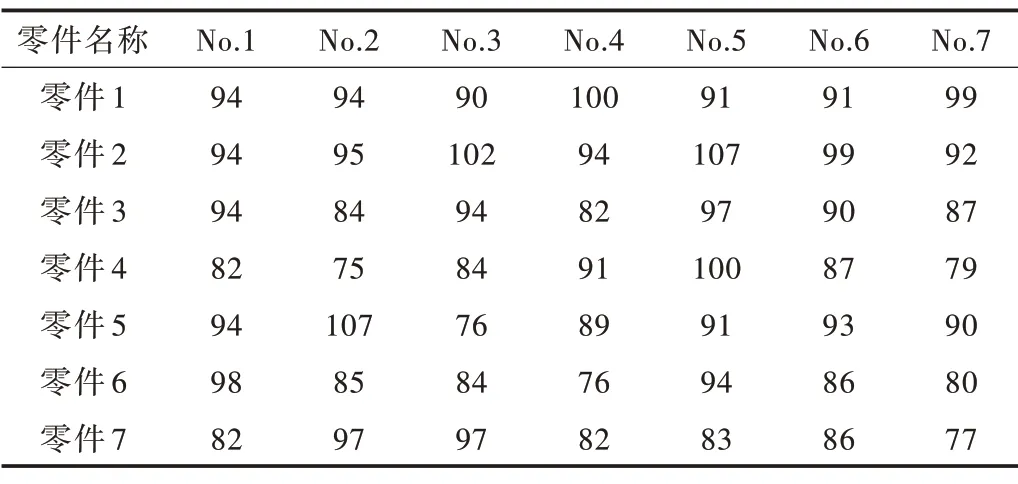
Table 2 Actual demand data of parts表2 零件实际需求数据

本文使用平均绝对百分误差、均方根误差和决定系数作为模型预测性能的评价指标［20］。

（1）平均绝对百分误差（MPAE）。MAPE 不仅计算真实值与预测值之间的差值，还考虑了该差值与真实值的比例。

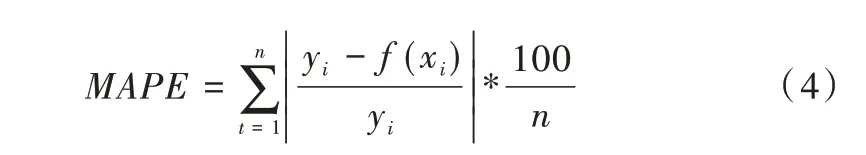
（2）均方根误差（RMSE）。方根误差对预测值误差大小十分敏感，能够很好地体现预测的精准度。

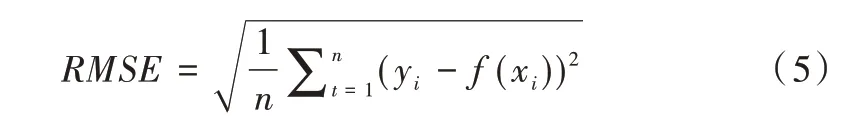
（3）决定系数（R2score）。决定系数用于判断回归方程的拟合程度，可以用于衡量模型预测能力，决定系数越大表示模型的预测性能越好，计算公式如下：

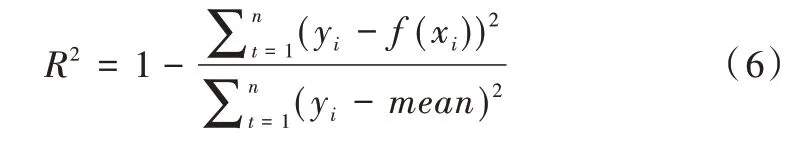
在λ=750、λ=1 350 和λ=1 900 时在测试集上进行测试，4 种零件预测结果评价指标如表3 所示。

当决定系数R2超过0.85 即可认为模型具有较好的预测性能［21］。通过需求预测性能实验可以看出，LSTM-CSP（λ=750，1 350，1 900）具有良好的预测性能，其中λ=1 350时，4 种零件整体预测效果最好。对比3 次实验发现，λ=1 350 时其均方根误差（RMSE）和平均绝对百分误差（MPAE）要小于λ=750 和λ=1 900 的值。

Table 3 Evaluation index of LSTM-CSP表3 LSTM-CSP 的评价指标

选取5 个连续的主生产计划（35 天）进行实验，当λ=1 350 时，部分零件的预测结果拟合程度如图4 所示。

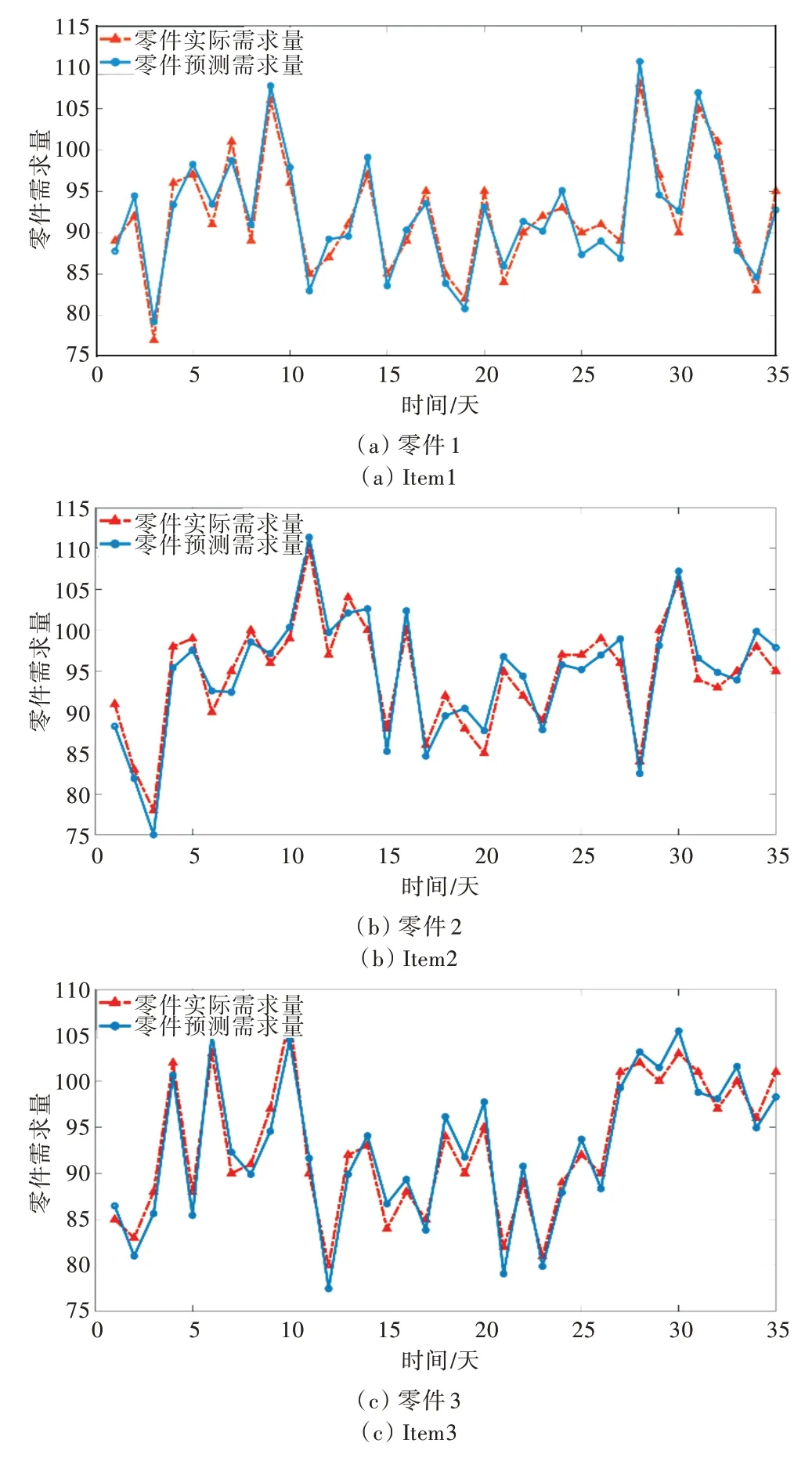
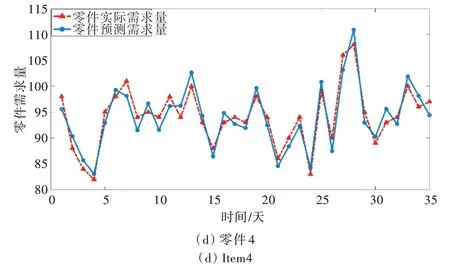
Fig.4 Fitting figures of prediction of cutting parts图4 零件的预测结果拟合程度

LSTM 网络在处理时间序列信息的延续性问题时，需要将λ个数据加入到细胞中。当λ从零开始增大时，细胞中有关数据增加，其预测性能不断提高。但是LSTM 网络的隐藏层信息容量（隐藏单元个数）是有限的，当λ增大到一定界限后会超过其饱和点，算法会出现过拟合现象，对后续数据不敏感，从而预测性能随之下降。此次需求预测性能实验中，当λ=750 时，LSTM 网络的隐藏层信息容量未达到饱和点，其预测性能未达到最优；当λ=1 900 时，LSTM网络的隐藏层信息容量超过饱和点，出现过拟合，其预测性能降低。因此，在使用LSTM-CSP 时需要选择合适的预测窗口λ。

在LSTM-CSP 中，不同的预测窗口会对预测精度产生影响，进而影响到下料的原材料利用率和原材料总成本。3 种预测窗口（λ=750、1 350、1 900）下原材料利用的总成本与利用率如表4 所示。

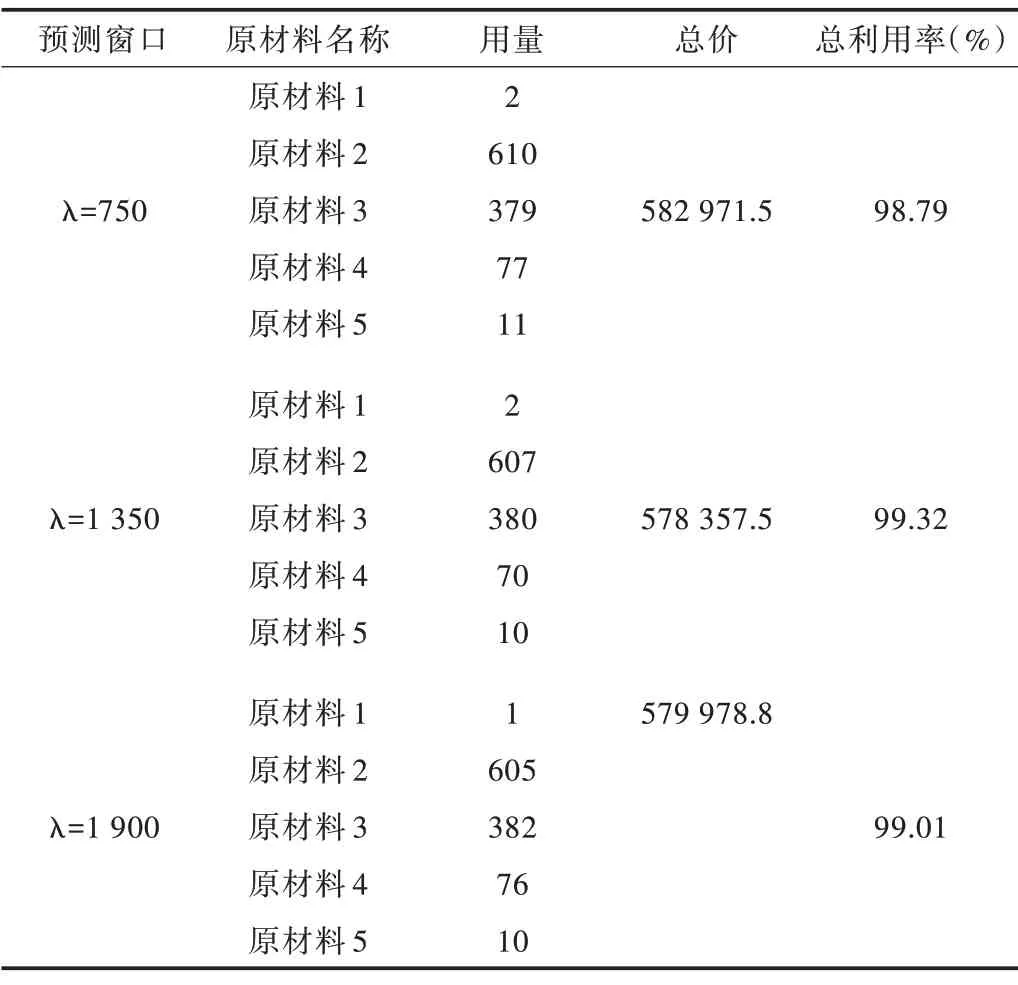
Table 4 LSTM-CSP blanking scheme under different forecast windows表4 不同预测窗口下LSTM-CSP 下料方案

通过零件需求预测性能实验发现，LSTM-CSP（λ=1 350）在原材料利用率上比LSTM-CSP（λ=750）和LSTMCSP（λ=1 900）都有大幅度提升。随着原材料利用率的提升，其成本也随之减少。因此，本文在优化性能对比实验中选择LSTM-CSP（λ=1 350）作为实验模型。

3.2.2 优化下料性能比较实验

为了验证所提模型的有效性，以单次下料（追求每个批次下料最优，不考虑余料的使用）和基于库存下料（追求每个批次下料最优，将余料纳入库存并在下次下料时优先使用）作为对照，进行对比实验。对比的指标分别为原材料利用率和原材料总成本。其中：

原材料利用率=零件总长度/原材料总长度

原材料总成本=原材料使用根数*原材料单价

单次下料算法对7 个批次进行优化下料，每次完成一个批次；基于库存下料算法对7 个批次的优化下料问题进行下料，每一个批次下料完成后将余料加入到库存中，并在下一批次中优先使用库存余料。两者的下料方案总成本如表5 所示。

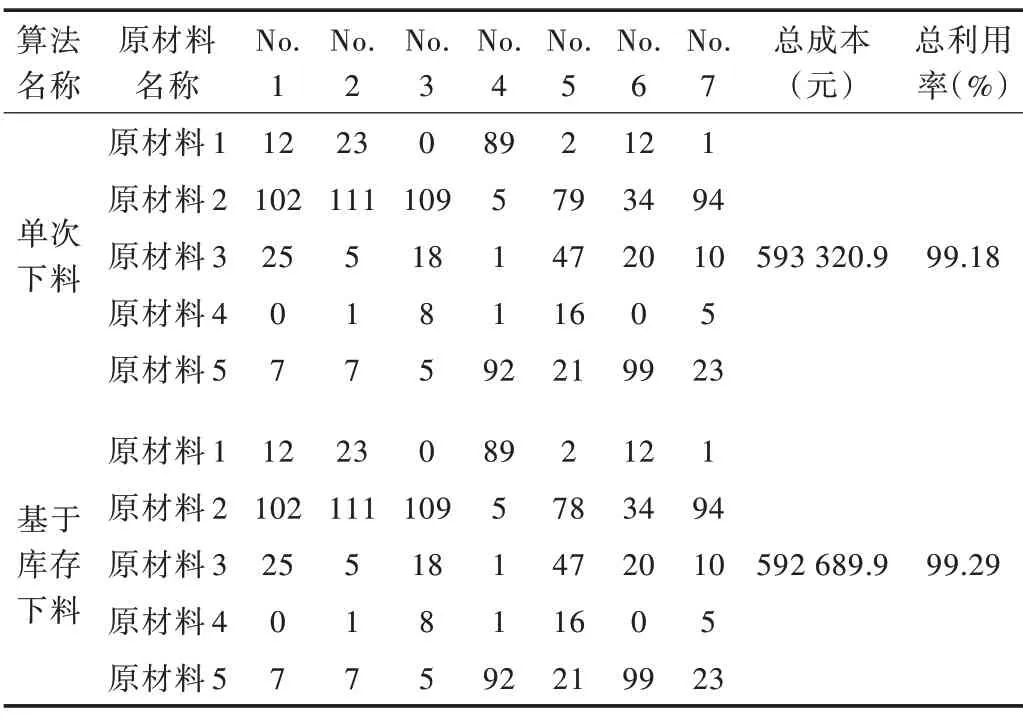
Table 5 Single blanking and optimization scheme based on inventory blanking algorithm表5 单次下料和基于库存下料算法优化方案

表6 给出每次下料中详细的预测需求。其中，零件1生产663件，零件2生产679件，零件3生产622件，零件4生产602件，零件5生产645件，零件6生产603件，零件7生产612 件。表7 给出每种原材料的下料用量与利用率。

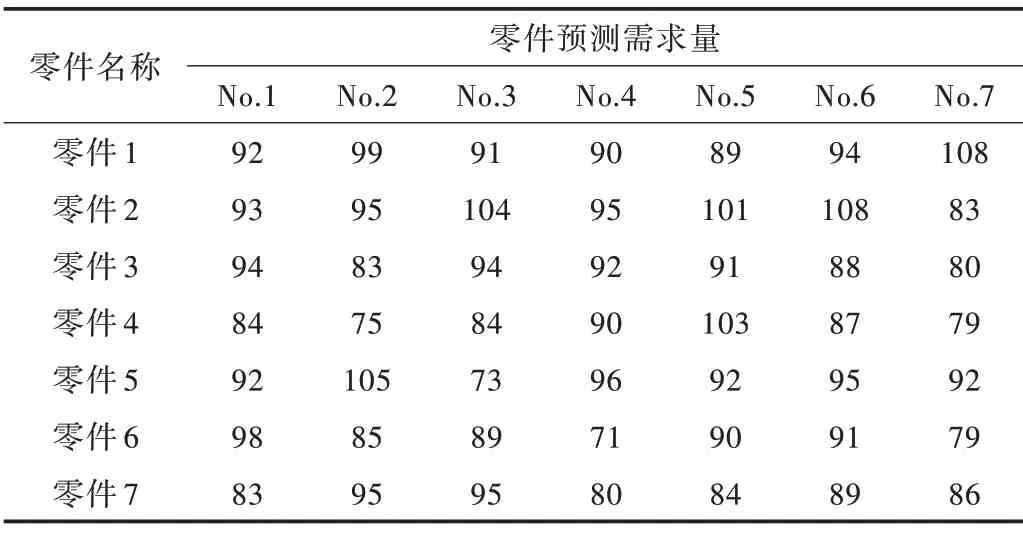
Table 6 Parts forecast demand data表6 零件预测需求数据

对比实际需求量后发现，零件1多生产2件，零件2少生产4件，零件3少生产6件，零件4多生产4件，零件5多生产5件，零件7 多生产8 件；因此，对少生产的零件再次下料。使用原材料5 和原材料3 进行补偿下料，两者各使用1根。表8 给出了LSTM-CSP（λ=1 350）算法的原材料利用率和原材料总成本。

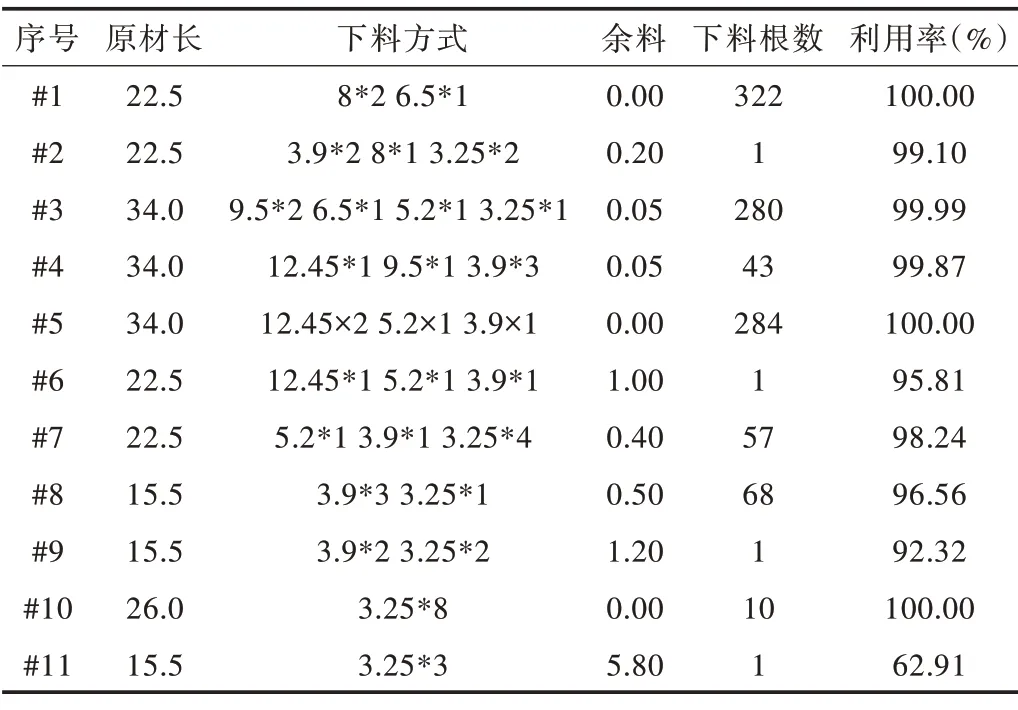
Table 7 Optimal blanking scheme of LSTM-CSP（λ=1 350）algorithm表7 LSTM-CSP（λ=1 350）算法优化下料方案

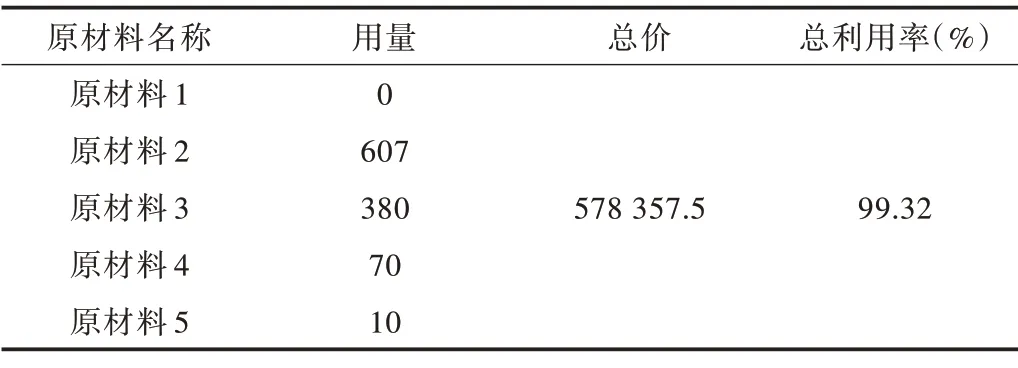
Table 8 Cost of blanking scheme of LSTM-CSP（λ=1 350）algorithm表8 LSTM-CSP（λ=1 350）算法下料方案成本

通过优化性能对比实验发现，LSTM-CSP 算法在原材料利用率上比单次下料和基于库存下料算法都有大幅度提升。随着原材料利用率提升，其成本也随之减少。相比于单次下料，LSTM-CSP 算法下料所得出的原材料成本更低，减少了14 963.4 元。LSTM-CSP 结合了集中下料思想，将零件的需求量进行纵向集中，扩大多批次型材优化下料问题的解空间。相比基于库存余料的型材优化下料算法，单独考虑了库存来扩大解空间范围，结果是LSTM-CSP 方法更加有效合理。

4 结语

本文针对多批次线型材料优化下料问题提出了一种融合LSTM 需求预测的下料方法，构建了相应模型LSTMCSP。该模型利用LSTM 对后续多个批次的零件需求量进行预测，将预测的需求整合成一个优化下料问题并利用列生成法进行求解，同时通过贪婪法对因预测误差造成的下料零件数量不足进行补偿下料。基于某型材加工企业的实际下料数据生成仿真数据集，进行仿真实验验证。优化下料性能比较实验结果表明，相比传统的按批次下料和基于库存下料方法，本文方法使线型材料多批次下料的原材料总体利用率得到提高，总成本显著减少。其中，与按批次下料方法相比提升了0.141 7%，金额减少了14 963.4 元；相比基于库存下料方法提升了0.031 3%，金额减少了14 332.4元。本文还对LSTM-CSP 算法中预测窗口λ 进行了研究，选取适当的λ 不仅可以有效降低时间复杂度，还可降低原材料总成本，提高原材料利用率。实验表明，本文方法能够有效提升线型材料多批次优化下料性能。后续将继续探索该方法在二维原材料优化下料中的应用。