非线性充电函数电动汽车配送路径问题研究
2022-01-07匡梓君
王 芳,秦 盼,匡梓君
(武汉科技大学恒大管理学院,湖北武汉 430065)
0 引言
近年来,随着工业的飞速发展,人们的生活水平不断提高,对汽车的需求量也逐步提升。因此,对环境造成的影响日益严重,其中包括对生态环境的破坏、对矿物资源的破坏以及对环境的污染等。普通汽车燃烧汽油供汽车行驶,并产生大量尾气。首先,产生的汽车尾气会污染空气;其次,汽油是不可再生化石燃料,在地球上的贮藏量有限。因此,清洁能源引起了人们的极大兴趣。
在该背景下,国家对绿色能源的关注与日俱增,计划到2022 年,初步建成布局合理、生态友好、清洁低碳、集约高效的绿色出行服务体系,绿色出行环境明显改善,绿色出行装备水平明显提升。电动汽车行业目前处于稳步发展阶段,发展前景良好[1-4]。另一方面,当前燃油价格不断上涨,且排放标准日益严格,物流企业纷纷采用电动汽车代替内燃机汽车,尤其在最后的配送环节中。
本研究具有以下意义:
(1)理论方面,可进一步丰富与发展电动汽车配送路径问题相关理论知识,为电动汽车电池电量计算提供了新方向,并为路径规划算法提供了理论依据,具有一定参考价值。
(2)经济方面,电动汽车行驶相同距离消耗的电力成本大约是传统汽车燃料成本的1/10~1/7。另外,如果电动汽车在低用电量期间充电(如在午夜,单位电价仅为中国部分省份正常电价的1/3),成本可进一步降低。
(3)环保方面,随着保护环境、节约能源的呼声日益高涨,电动汽车的环保特性(如没有温室气体排放、降低噪音污染、高能源效率)不仅对环境有益,而且可帮助使用电动汽车的物流企业树立更加绿色、健康的企业形象。
1 相关研究综述
就能量消耗而言,现有模型大部分采用线性函数近似方法[5-6],即电池能量增长随充电时间的延长而线性增长。然而,这种线性增长的方式过于理想化,实际应用中有很多额外因素都会对电量消耗产生影响。此外,即使为电池充相等的电能,从不同的电池状态开始充电,充电时间也会有很大不同。在这方面,Goeke 等[7]和Lin 等[8]在考虑电动汽车参数及其负载的情况下,使用实际道路网络计算电池能量消耗。谭学怡等[9]、赵雅兰[10]分析电动汽车质量、速度与道路坡度对电动汽车电量消耗的影响,构建了基于非线性电量消耗的电动车路径规划模型;蔡银怡[11]在分析电动车能量消耗影响因素与能量转换过程的基础上,构建更符合实际的能量消耗函数。为模拟更真实的充电过程,Montoya 等[12]引入带有非线性充电函数的电动汽车路径问题(E-VRP-NL),但引入非线性充电函数后,现有研究都对函数进行了线性化近似,而近似过程可能会对实验结果产生影响[13-14]。因此,本文首次不对非线性充电函数进行线性化近似,而是直接使用。
目前已有的电动汽车配送路径方案中,针对电动汽车充电问题,主要存在两种解决方法:①通过复制充电站生成多个充电站的虚拟节点解决充电站访问问题,每个充电站最多只能被一辆车访问一次[15-16],但是这种解决办法有很大缺陷。一方面,当充电站数量很多时,将增加问题的复杂性。另一方面,设置虚拟充电站时无法预知每个充电站的虚拟节点数目;②通过设置一个决策变量Xijc判断电动车在从客户i到客户j的路径中是否访问了充电站,访问充电站时,决策变量Xijc=1,否则Xijc=0,但是这种方法同样会增加问题的复杂性[17-18]。
Zuo 等[19]提出一种新的更为高效的方法解决车辆访问充电站问题,使用该方法时,其模型复杂度高于传统VRP模型。N表示客户节点集,N′表示客户与仓库的集合。首先为每个客户定义一组附近的充电站Ci(Ci∈C),然后引入一个二进制变量yic,说明车辆在离开客户之后是否访问充电站,访问即yic=1,否则yic=0。该变量的引入不增加模型复杂度,因此本文模型沿用此二进制变量。
2 模型构建
本文沿用文献[19]相关假设,假设穿过节点弧(i,j)时的电能消耗是一个常数dij(根据标准距离单位(SDU)2测量),并假设弧上消耗的能量等于弧距离(单位:sdu),而行程时间也等于以分钟为单位测量的弧距离。本文使用的充电函数是Teo 于2015 年拟合的[20]。经过计算,电池电量充满大约需要108min(见图1)。

Fig.1 Non-linear charging function图1 非线性充电函数
函数斜率即电动车电池充电速率,通过观察函数可看到函数斜率随时间的增长呈下降趋势,也即是说电池充电效率随着时间的增长不断降低。并且,当电池从不同的电量状态开始充电,需要充相同电量时,起始电池电量越多,充电时间越长。具体而言,同样为电池充0.1的电,从电池状态为0.2时开始充,所需时间为14.184 6-9.192 3=4.992 3min,而从电池状态为0.7时开始充,所需时间为52.695 4-42.382 5=10.312 9min,所需充电时间显著增加。
2.1 问题描述
电动汽车配送路径问题为一组已知地理位置、需求、服务时间窗和服务时间的客户进行配送服务,服务车辆是一组已知车辆容量、车辆最大行驶距离和电量消耗速率的同质车队。车辆在行驶过程中,电池剩余电量随着行驶距离的增加而下降,车辆可在充电站充电后继续行驶,充电站数量及位置已知。
目前研究电动汽车路径问题时,针对电动车行驶过程中的能耗问题,大部分学者引入的是线性充电函数,也即充电能量与充电时间成正比,但实际上大多数电动汽车充电能量与充电时间不成正比,充电速率随着充电时间的增加而逐步下降。
该问题的目标是规划可行的路径方案并使其行驶里程最小,可行方案需满足以下条件:为每个客户服务并且只服务一次。到达每个客户点以及最后完成配送任务回到仓库都在规定的时间窗内。电动汽车在路径上任一点,电池电量都在0~Q 之间。
2.2 基本假设
所有客户只能被一辆车服务,不允许订单拆分。
允许充电站被多次访问。
假设每个CS 具有同时为多个EV 服务的无限容量。
假设这些站点的所有电动汽车具有相同的SOC 时间曲线。
电动汽车从仓库出发时是满电状态。
假设路网处于恒定的交通环境中。
车辆的行驶速度恒定。
2.3 数学模型
相关参数如下:

决策变量如下:


问题的数学模型如下:

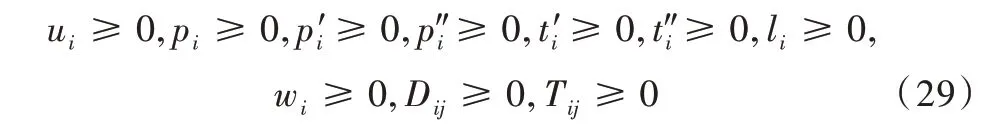
公式(1)为目标函数,表示总行驶里程最小;公式(2)、(3)表示每个客户只能被访问和离开一次;公式(4)判断车辆是否在离开客户i后访问充电站;公式(5)-(8)计算车辆从客户i到客户j的实际行驶里程;公式(9)确定行驶时间;公式(10)、(11)跟踪路径上的时间;公式(12)、(13)显示仓库点不需要服务;公式(14)为客户i开始服务的时间在可以为客户i进行服务的时间窗口内;公式(15)指电动车在到达客户i时车辆负荷不小于客户需求;公式(16)、(17)跟踪路径上车辆的负载;公式(18)指车辆在路径上任意位置的负载不大于车辆最大容量;公式(19)、(20)限制行驶到客户途中的能量变化;公式(21)限制行驶到仓库途中的能量变化;公式(22)、(23)限制行驶到充电站途中的能量变化;公式(24)说明车辆是满电量从仓库出发的;公式(25)指车辆到达充电站时剩余能量不小于安全阈值;公式(26)保证充电后电动车能量不超过最大电池容量;公式(27)约束了电动车充电时间;公式(28)、(29)定义了所有决策变量范围。
3 启发式方法
3.1 时间窗优先的求解方法
时间窗优先的求解方法即将各客户按可以服务的截止时间升序进行排序,然后对排序后的客户逐一进行判断求解,无法服务的客户直接放入下一轮重新判断,直到所有客户都完成配送服务,如图2 所示。具体流程如下:
Step 1 初始化参数。初始车辆数为0,初始里程为0。
Step 2 计算客户、仓库及充电站各点间的距离,生成距离矩阵。构造当前无法服务的客户点集Qw,并将未服务的客户点按可以服务的截止时间升序进行排序,将排序后的客户点集存入Q 中。
Step 3 判断Q 中个体数是否等于0,若等于0,则操作终止,输出最优路径;否则,转Step 4。
Step 4 按Q 中的客户排序判断每个客户点能否为其服务。
Step 4.1 判断服务当前客户点是否满足时间窗与容量需求,并判断如果进行服务,之后能否在指定时间窗内回到仓库点。若满足要求,则转入Step 4.2;否则,转入Step 4.5。
Step 4.2 判断如果进行服务,服务完成后剩余电量能否回到仓库或充电站。如果可以,则进行服务并更新数据,转到Step 4;否则,转入Step 4.3。
Step 4.3 判断剩余电量能否直接到达充电站。若满足要求,进入充电站充电,并转入Step 4.4;否则,转入Step 4.5。
Step 4.4 判断充电并服务完当前客户后是否仍能回到充电站或仓库。若满足要求,对其进行服务并更新数据;否则,转入Step 4.5。
Step 4.5 将当前客户加入未服务点集Qw 中。
Step 5 判断服务完最后一个客户后能否回到仓库。
Step 5.1 判断服务完最后一个客户后车辆能否回到仓库。若满足要求,更新数据,并转到Step 3;否则,转到Step 5.2。
Step 5.2 判断服务完最后一个客户后能否回到充电站。若满足要求,则转到Step 5.3;否则,去掉最后一个服务的客户点,转到Step 5.1。
Step 5.3 判断允许充电的最大时间是否大于回到仓库所需充电的时间。若满足要求,则回到仓库,更新数据,并转到Step 3;否则,去掉最后一个服务的客户点,转到Step 5.1。
3.2 距离优先的求解方法
距离优先的求解方法即在未服务点集中选取离刚服务的客户最近的满足时间窗、电量及车辆容量等约束的客户点进行配送服务,直到所有客户都完成配送服务的过程,具体流程如图3 所示。
由图3 可清晰地看出,以距离为优先的求解方法在整个循环逻辑上与以时间窗为优先的求解方法基本一致,主要区别在于选取即将服务的客户时参考数据不一样(文字进行了加粗),时间窗参考的是可服务客户里可服务截止时间最早的一个,而距离优先选取的是与刚服务的客户距离最近的客户,以致中间数据更新环节有一些不同。
3.3 节约里程法
节约里程法[20]是指依次将运输问题中的两个回路合并为一个回路,每次使合并后的总里程减少最多,直到达到车辆的最大载重量,再进行下一辆车的优化。首先根据节约里程公式计算连接每两点相应的节约里程数,然后在未服务点集中选取与刚服务的客户连接时,节约距离最大的满足时间窗、电量及车辆容量等约束的客户点进行配送服务,直到所有客户都完成配送服务。
与时间窗优先及距离优先一致,节约里程法在循环逻辑上也与前两者相同。不同的是节约里程法选取即将服务的客户时,参考的是闭合两个回路成一个回路时产生的最大节约距离,这里不再赘述。
3.4 同时考虑时间窗与距离的求解方法
该方法在考虑下一个可配送客户时,还使用线性加权方法,将时间窗优先与距离优先同时考虑进来,二者的权重系数相加为1。本文设计了0.2/0.8、0.4/0.6 两种权重比例。
4 结果比较与分析
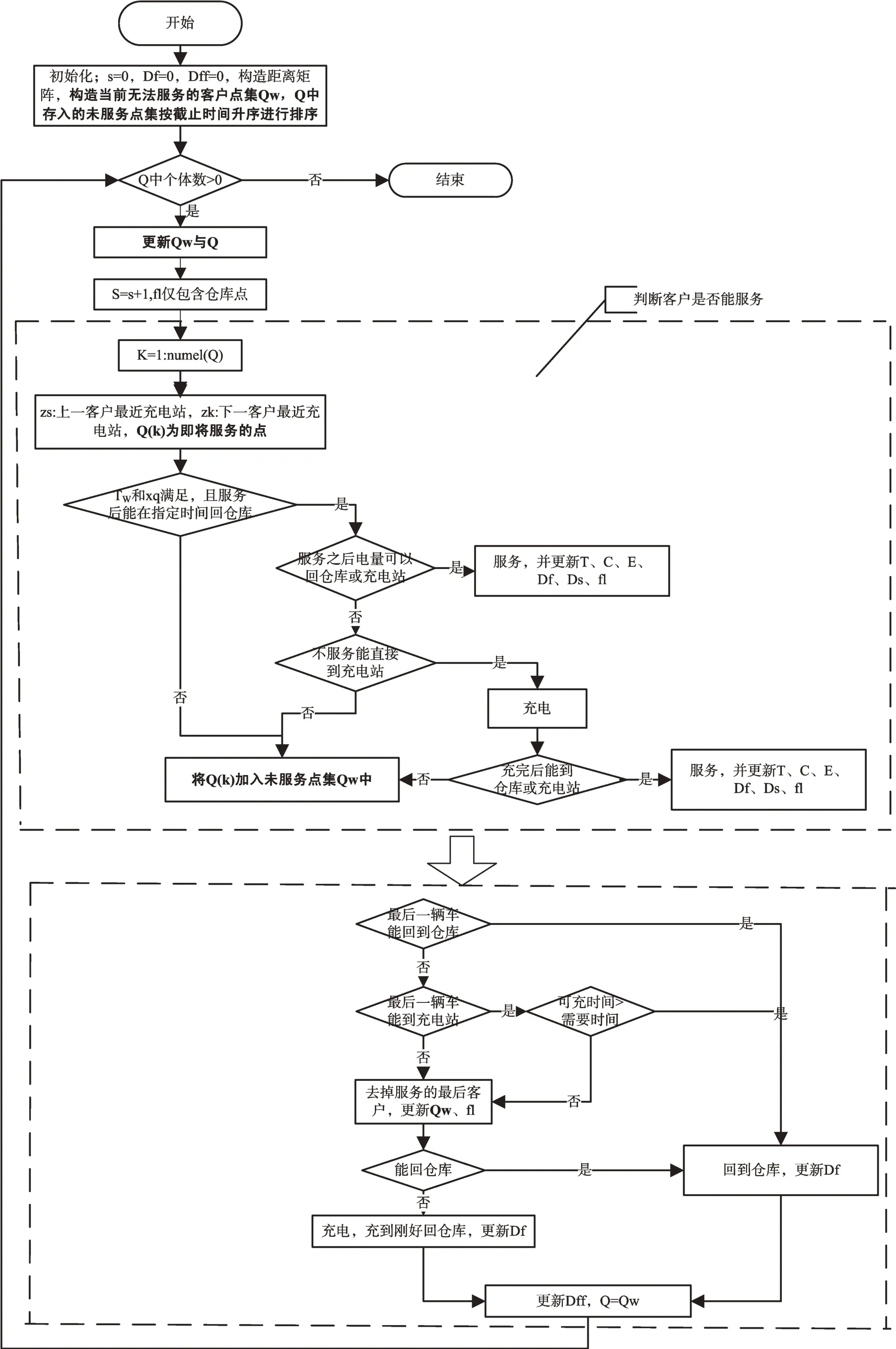
Fig.2 Time window first solution method图2 时间窗优先的求解方法
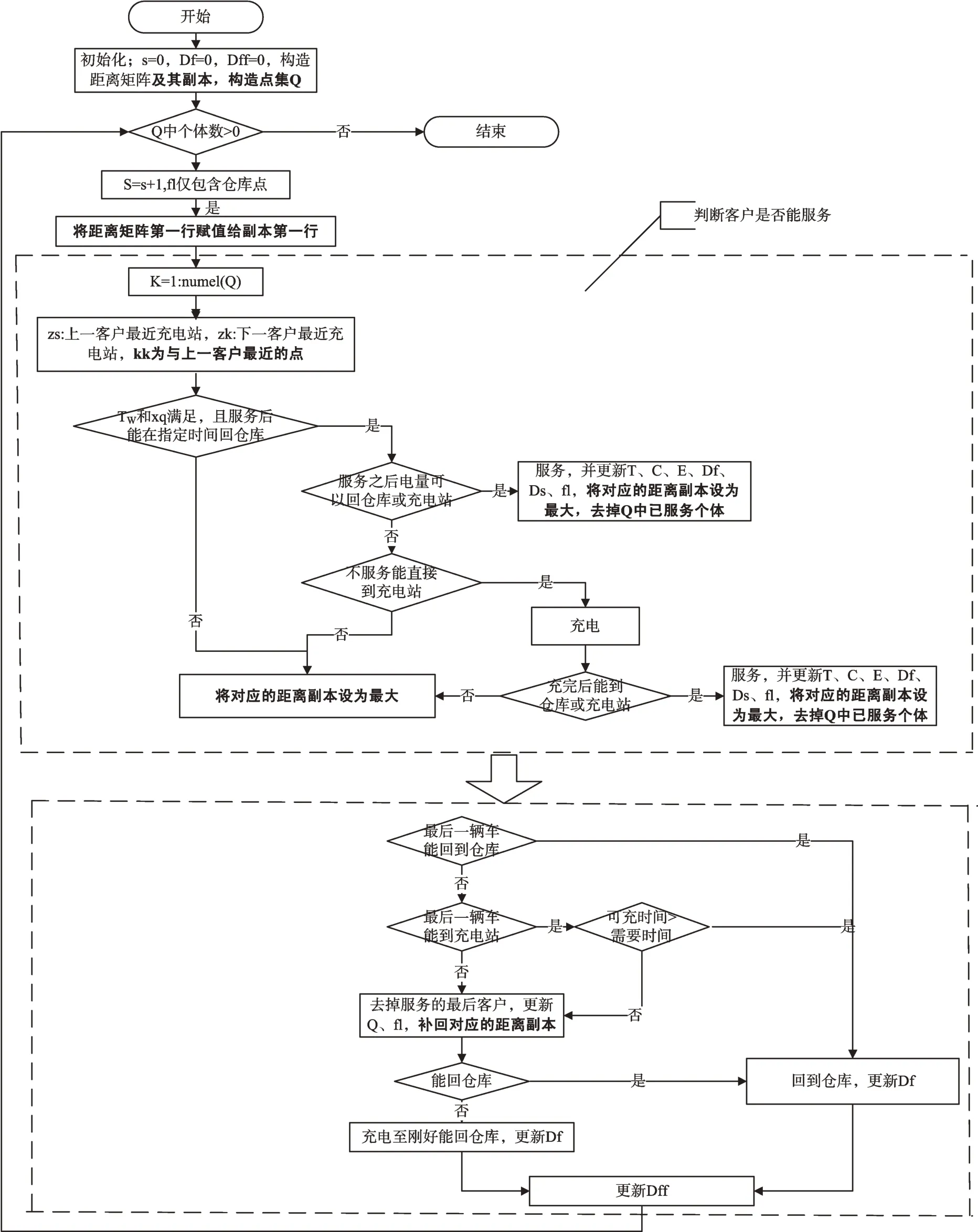
Fig.3 Distance-first solution method图3 距离优先的求解方法
本文使用经典Solomon 的VRPTW 实例[20],集合C 中的客户地理数据呈聚集性特点,而集合R 中的客户地理数据是随机分布的。集合RC 中的客户地理数据结合了随机与聚集两个特点。R 型和RC 型问题的客户服务时间为10,C型问题的服务时间为90。其中,充电站横坐标由计算得出,纵坐标由计算得出,i、j表示客户点。
采用不同求解方法,针对不同客户集合类型进行求解,并将结果与现有数学模型求解结果进行对比分析,如表1 所示[19]。
经过对数据的观察对比,对于R 类客户集合,使用节约里程法得到总里程的AVG 值最大,而使用距离与时间窗加权的方法得到的结果最小,其中0.4/0.6 权重的平均结果最好。几种方法得到的结果均优于现有数学模型求解结果,而其中表现最优的为0.4/0.6 权重方法。对于C 类客户集合,表现最差的依然是节约里程法,表现最好的为时间窗优先的求解方法。0.2/0.8 权重方法在单个案例中表现较好,有C102-104 共3 个案例的求解结果优于数学模型的结果。而对于RC 类客户集合,表现最差的是距离优先的方法,表现最好的为0.2/0.8 权重方法。不论哪种方法都能求出可行解,而采用CPLEX 求解在某些案例中甚至求不出可行解,并且好的启发式方法可求得比CPLEX 更好的解,尤其是综合考虑时间窗与路径的求解方法表现较好。

Table 1 Comparison of experimental results表1 实验结果比较
5 结语
本文考虑有客户需求、车辆容量和电池容量等约束的车辆路径问题,并在电池容量计算中引入非线性充电函数,同时使用一种新的模型构建方法。该方法都能对问题进行快速求解,并且相当一部分案例能获得比数学模型求解更好的结果,说明启发式求解方法在求解大规模问题时具有一定优势。本文设计的求解方法较为简单,下一步可对求解方法进行改进,以进一步提高寻优能力。
