基于误差约束的激光扫描路径优化研究

殷亚斌，张立强，周六信，李宇昊

（1.上海工程技术大学机械与汽车工程学院；2.上海拓璞数控科技股份有限公司，上海 201620）

0 引言

3D 线激光扫描仪可将从物体表面搜集的密集坐标数据点作为点云快速捕获物体的表面几何形状，具有非接触测量、测量速度快、光学排列简单、精度适中、成本低、易提取光条纹图像信息等优点。然而，3D 激光扫描仪扫描出的点云质量会因工件表面的镜面反射而产生微小的测量误差，与工件表面点的真实位置不同，点云数据亦会因为不同的扫描深度和角度而造成不同程度的误差。这些误差会对后续计算机辅助设计与应用程序开发产生负面影响，在逆向工程中也会导致建模误差。因此，在利用3D 线激光扫描仪对反射面进行扫描时，分析影响扫描精度的主要参数十分必要。

针对工件表面颜色造成的扫描误差，Li 等［1］建立了材料颜色、吸收颜色、波长三者之间的库表示测量误差与颜色之间的关系，认为通过误差库补偿误差较为可行；Dang等［2］针对颜色测量中由于角度不同而产生的颜色偏差，记录x、y 色度坐标，利用LASSO 函数拟合与交叉验证，并建立色度坐标偏移预测模型，进行了精度评价；Vukasiinovic等［3］研究了工件表面颜色与工件和传感器的距离对激光扫描误差的影响。针对扫描位姿造成的误差，Lu 等［4］研究了倾角和方位角（包括旋转角和偏转角）对测量结果的影响，基于误差补偿构造迭代函数，提出一种任意位置和方向激光的标定方法，并进行了误差补偿；任永杰等［5］研究系统测量精度与转台转角之间的关系，建立了角度与精度测量模型；Wu 等［6］研究激光扫描仪的位置和姿态参数（包括扫描深度、入射角和方位角）对测量误差的影响，建立了基于几何光学的理论模型和基于误差评估的经验模型；Feng 等［7］研究扫描深度和扫描偏角对测量精度的影响，发现系统误差与扫描深度和扫描偏角呈双线性关系；Igor 等［8］通过过滤扫描仪的随机误差结合三坐标测量机数据估计被检测工件的形状偏差，利用较少的触觉点有效补偿了点云位置误差；王建军等［9］研究姿态角随机测量误差与点云、数字表面模型之间的联系，通过建立姿态角随机测量误差与激光脚点定位误差之间的关系优化姿态角，降低了扫描误差；Crane 等［10］将一种基于热流计算距离的新方法应用于求解测地线距离，该法还可以应用于任何类型的域（点云、三角网格、多边形网格等），在点云中计算出任意两点的误差，速度较快，且平均误差较小；周森等［11］通过两个固定的激光扫描仪获取工件两端表面的关键轮廓，通过高度特征变化识别端面、端点位置，并结合空间投影和最小二乘原理拟合出关键数据，以提高扫描精度；Wang 等［12］研究扫描方向对离群点的影响，开发了一种检测和去除离群点的有效方法，结果发现正确的扫描方向可以显著减小异常值范围；何秉高等［13］研究温度对激光发射、接收光机系统的影响，提出一种三维激光扫描定位系统优化方案，提高了扫描精度；王鹏等［14］利用背光板获取不同角度下被测工件的背影轮廓，并运用所得表面数据设置扫描路径，最终获取了完整的工件表面点。通过查阅大量文献可知，现有研究多集中在点云数据补偿［15］、边缘信息处理［16］，以及工件表面颜色［17］、工件表面误差数据［18-19］、粗糙表面数据［20］对扫描精度的影响等方面。

目前很多研究聚焦扫描位姿对扫描误差的影响，未利用扫描位姿对五轴机床中的线激光扫描进行路径规划。为此，本文针对线激光扫描仪的测量误差，提出一种扫描路径规划方法，将扫描误差作为目标函数，最小化每个扫描位姿的扫描误差，获取当前位置的扫描位姿，并组成位姿集合，作为扫描路径。具体操作为首先引入激光扫描误差ε 与扫描角度、扫描深度之间的关系；然后构建目标函数，通过优化目标函数选择当前最佳扫描位姿，获得扫描路径上的扫描姿态集；最后对所提出的线激光扫描路径进行实验分析，通过与常规中间扫描路径进行对比验证本文方法的有效性。

1 激光扫描原理

图1 为典型的3D 线激光扫描系统，包括1 个五轴机床，1 个安装在五轴机床主轴上的3D 线激光扫描仪，1 个具有自由曲面的工件。五轴机床的主轴用于安装线激光扫描仪，规划扫描路径，扫描方向为点光源位置T 到工件表面点P。线激光扫描仪分为两个部分，一个是激光源T，用于发射激光到工件表面点P；另一个是传感器Q，用于接收远离工件表面的漫反射光线。

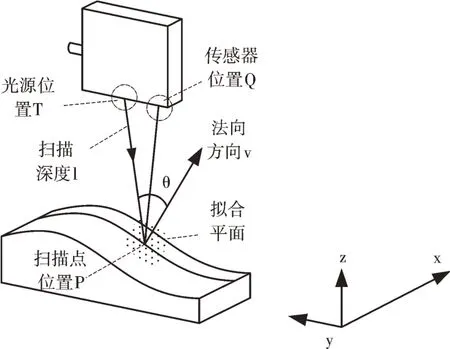
Fig.1 System of laser scanning图1 激光扫描系统

如图2 所示，激光扫描仪发射出激光，与工件表面形成扫描深度l，与工件表面点P 处的法线方向形成扫描倾角θ。文献［21］通过线激光扫描仪扫描标准球得到误差ε、扫描倾角θ 与扫描距离l 三者之间的关系，表示为：

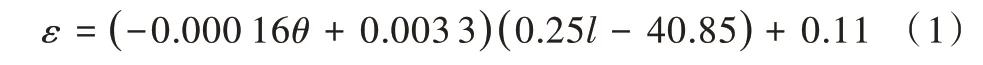
当θ=0，ε=0 时，可以计算出最佳扫描深度为lb=2255/126。

Fig.2 Scanning angle and scanning depth图2 扫描角度与扫描深度

2 扫描路径优化

2.1 工件表面离散点及其扫描位姿获取

扫描层工件表面离散点的集合为P｛P1，P2，P3，…，Pn｝，与各点对应的最佳扫描位姿集合为T｛T1，T2，T3，…，Tn｝。如图3 所示，集合P 与集合T 中的点一一对应，扫描深度均为最佳扫描距离lb，对应方向均为集合P 中每个点在其局部区域的法向。

Fig.3 Discrete points and scanning points on workpiece surface图3 工件表面离散点及其扫描点

采用最小二乘法计算出点P 处拟合平面的法向Vi（ui，vi，wi）。通过建立局部扫描姿态坐标系，由Pi［xiyizi］位置、扫描法向Vi［uiviwi］以及最佳扫描距离lb经过空间平移变换，可以确定与Pi对应的Vi的位置，表示为：

2.2 优化目标函数建立

理论上集合T 中的每个点都可以作为该处线激光扫描仪的扫描位姿，但在实际操作中，一般会选取工件表面中间点作为扫描位姿，然而其不一定为最佳扫描位姿，需要进一步优化。创建每个扫描位姿的误差函数以量化扫描误差，比较目标函数大小，误差最小值即为最佳扫描位姿。

定义误差集合K｛K1，K2，K3，…，Kn｝，Ti位姿下Ti与离散点集合P｛P1，P2，P3，…，Pn｝中各点形成扫描距离集合li｛li1，li2，li3，…，lin｝以及扫描角度集合θi｛θi1，θi2，θi3，…，θin｝，则该扫描位姿处的扫描误差为：

式中，εij为扫描位姿Ti与第j 个工件表面离散点的扫描误差。各参数如图4 所示，计算方法如式（4）所示。

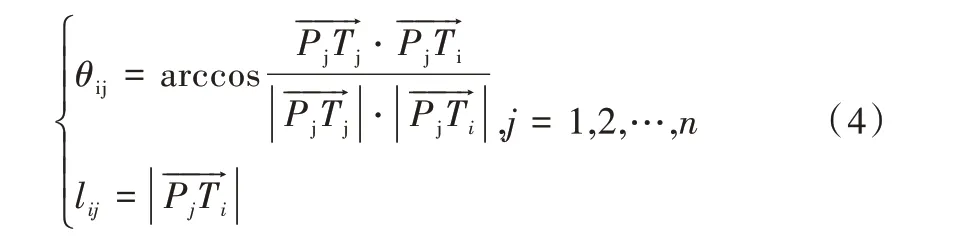
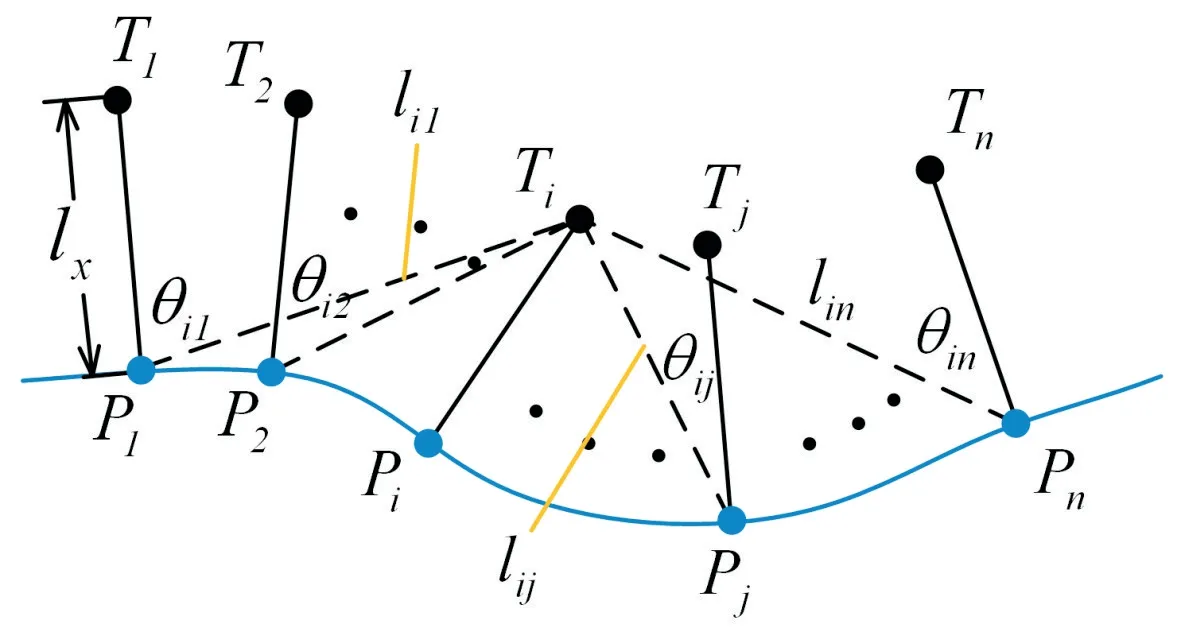
Fig.4 Scanning angle and scanning depth under each scanning position and pose图4 各扫描位姿下扫描角度与扫描深度

找出Ki中的最小值Kmin，记录当前扫描层对应的最佳扫描点Tbi，每一层的扫描点集合即为扫描路径，表示为Tb｛Tb1，Tb2，Tb3，…，Tbh｝，其中h 表示该扫描路径上所有的扫描层数。

综上所述，算法总体流程为通过扫描深度和扫描角度两个因素建立误差优化目标函数；然后离散曲面，获取点云，得到不同点位处的扫描位姿；构建不同扫描位姿下的误差函数，计算最小误差并获取当前扫描位姿以构成扫描位姿集合，最终形成扫描路径。具体如图5 所示。

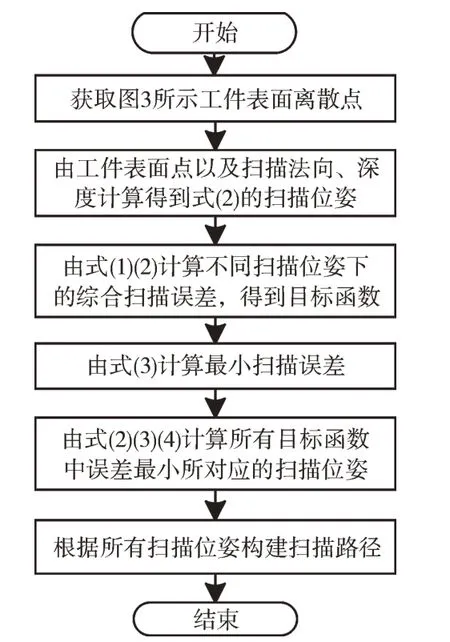
Fig.5 Flow chart of scanning path algorithm图5 扫描路径算法流程

3 实验方法与结果

3.1 仿真结果分析

对每层每个点的扫描位姿及其对应扫描误差进行分析，结果如图6 所示（彩图扫OSID 码可见）。扫描层数为6，每层扫描位姿为39 种，对应图中横坐标，每个位姿下的扫描误差Ki对应图中纵坐标，优化前的扫描路径均为每层第20 个扫描位姿，即图中虚线对应位姿。通过仿真发现，第20 个扫描位姿并非扫描误差最小的位姿，最佳扫描位姿实际上分布在中间扫描位姿周围。

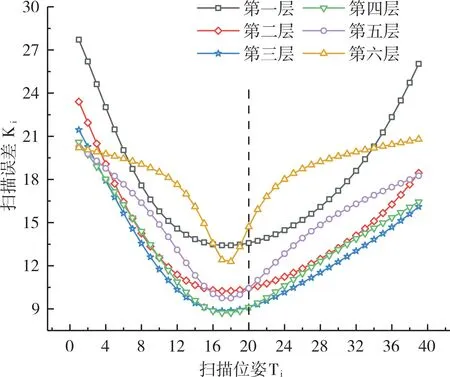
Fig.6 Scanning position and scanning error data图6 扫描位姿及扫描误差数据

优化前后扫描误差比较如图7 所示，x 轴表示扫描层数h，y 轴表示优化前后的误差大小。可以看出，优化前后误差随着扫描层数的增加呈先降低后增加的趋势。

Fig.7 Error before and after optimization图7 优化前后误差

由图8 可知，基于扫描误差的位姿优化方法会使优化幅度随着工件表面平均曲率的增大而增大，平均曲率的变化范围为0.113～0.514，优化幅值对应的变化范围为0.161～2.420，这表示对于表面曲率越大的工件，优化后扫描误差的降低幅度就越大，优化效果越明显，即在曲面变化幅度较大时使用本文方法优化效果更好。

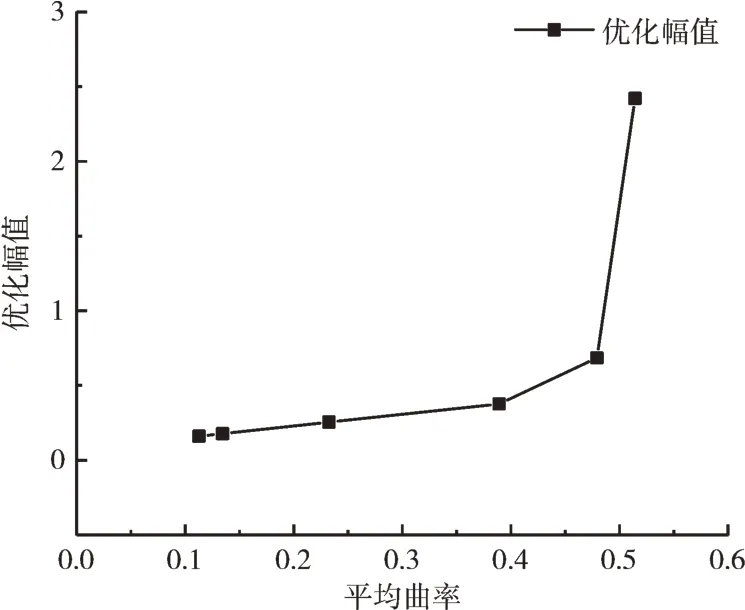
Fig.8 Mean curvature and optimized amplitude图8 平均曲率与优化幅值

3.2 对比实验与结果分析

使用基恩士LJ-V7300 激光扫描仪进行验证实验，其平面不确定度为Z 轴5μm、X 轴60μm，可接受的仰俯角度为±45°。采用BC 双摆台摇篮式五轴机床VMCC30H，其中B 轴旋转幅度为±90°，C 轴旋转幅度为±180°，工件通过夹紧装置固定在工作台上，通过控制五轴机床运动可以达到任意扫描位姿，如图9 所示。采用ZEISS CONTURA G2 三坐标测量机，其精度可达1.8μm+L/300，测量环境如图10 所示。

将三坐标测量数据作为工件表面实际数据，对扫描得到的点云数据与实际数据进行对比。采集15×39 个点的工件表面数据，计算点云数据中的点与三坐标中对应点之间的距离，并作出对应误差图，其中标准线以下记为负数，标准线以上记为正数。图11 为优化前后误差对比图（彩图扫OSID 码可见），其中图11（a）为优化前沿中间法线的扫描路径，图11（b）为优化后的扫描路径。从图中可以看出，误差主要集中在蓝色和深红色区域，对应曲面上曲率较大且距离标准线较远的区域。优化前的扫描路径基本在曲面中间，即表面离散中间点对应的扫描位姿，此时误差比较对称。优化后的路径稍微偏左，最左边扫描区域的整体扫描误差相对减小，最右边区域由于扫描深度与扫描角度的增大导致局部扫描误差变大，误差范围由-0.017～0.018 变化为-0.019～0.012 9，但总体误差减小，根据区域曲率不同，误差降低1.184%～16.450%。如果曲面曲率变大，扫描区域随之变大，整体可以降低的扫描误差也会更大，优化效果也会更明显。

Fig.9 Environment of laser measuring图9 激光测量环境

Fig.10 CMM environment图10 三坐标测量环境

4 结语

本文针对线激光扫描仪扫描获取工件表面轮廓过程中，因扫描深度和扫描角度不断变化而导致点云扫描误差较大的问题，提出适用于线激光扫描的扫描路径规划策略。根据激光扫描特性，充分利用不同扫描深度和扫描角度构成的扫描误差优化扫描位姿，构建最小扫描误差下的扫描路径。该法虽然会导致局部扫描误差增大，但整体误差却会减小，平均曲率的变化范围为0.113～0.514，优化幅值对应的变化范围为0.161～2.420，误差降低1.184%～16.450%。随着扫描曲面曲率的增大，优化后扫描误差的降低程度也越大，有效证明了本文提出方法的有效性。然而在进行点云分区时，阈值的选择会直接影响曲面分区的大小以及线激光扫描路径的规划，本文在选取点云的曲率阈值时未涉及到曲率选值标准的考察，后续可深入对点云曲率阈值进行研究。

Fig.11 Error distribution before and after optimization图11 优化前后误差分布