粒子群优化LSSVM 与RBF 的混合回归预测模型

2022-01-07王博，彭硕

软件导刊 2021年12期

王博，彭硕

（井冈山大学电子与信息工程学院，江西吉安 343009）

0 引言

支持向量机（SVM）具有良好的鲁棒性，已广泛应用于模式识别、回归分析、趋势预测等领域。由于支持向量机模型中的两个正则函数与核参数具有优化改进的空间，例如文献［1-3］提出对正则参数使用参数优化算法，并对传统的支持向量机进行改进，取得了良好效果。其中，游仕洪等［3］注意到，传统支持向量机在进行训练时，输出的误差项包含大量可再次学习的信息，因此提出新的混合回归预测模型来提取这些信息，并再次训练输出，得到了更优的输出；文献［4-6］则对核参数进行优化；文献［7-9］采用ARIMA-SVM（混合时间序列预测算法）将数据的线性训练数据与非线性预测误差相结合，得到最终预测结果；文献［10］建立支持向量机与泰勒时间预测混合模型，对残差项重新进行优化训练，对支持向量机的预测值进行修正。

然而，上述混合模型受限于训练数据的线性要求，使模型应用范围受到限制。本文尝试将最小二乘支持向量机与经过粒子群算法优化的RBF 神经网络相结合，建立混合回归预测模型（LSSVR-IPSO-RBFNN），并将该模型用于流域水生态环境的水质预测，取得了良好效果。

1 支持向量机与最小二乘支持向量机

支持向量机理论基于结构风险最小化原则，利用样本信息，在提高特定训练样本学习精度及任意样本识别精度的需求中寻找最佳点，以解决受约束的二次规划问题，具有较好的预测能力。由于支持向量机本身的特性，其在回归分析、模式识别等领域得到了广泛应用，并取得了很好的效果［11-13］。

以下函数常被用来描述支持向量机的优化问题：

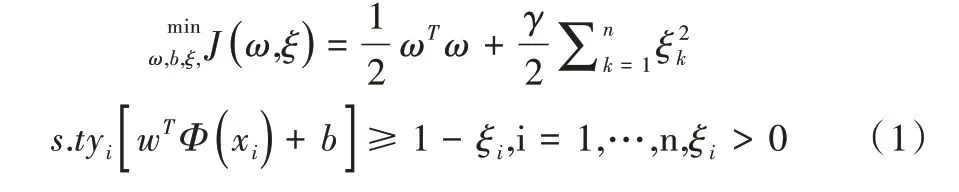
利用拉格朗日法对上述公式进行优化求解，将其转化为二次规划问题。

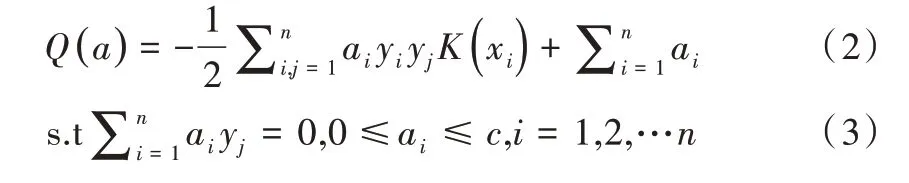
虽然支持向量机具有较好的预测能力，但训练过程复杂、计算速度较慢。最小二乘支持向量机模型将整个训练过程简化为求解一个线性方程组，可有效避免求解二次规划问题，因此减少了计算量，提高了计算速度。最小二乘支持向量机相较于标准支持向量机过程更加简单，建模速度更快。具体公式如下：

在此基础上引入拉格朗日公式，表现为以下形式：

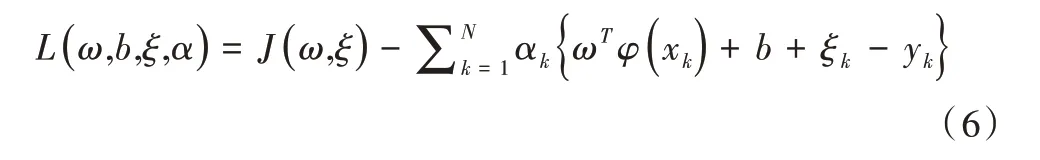
进一步推出优化条件为：

转换为矩阵，表示为以下形式：

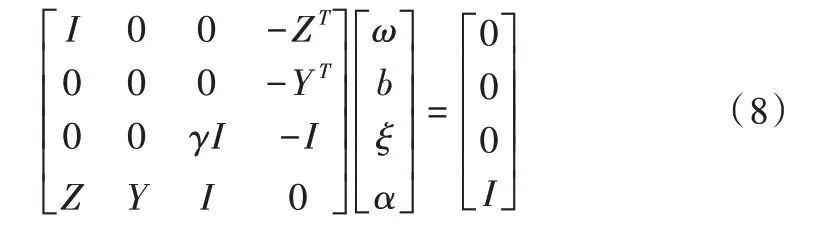
式中，I是n×n 的单位矩阵，，。消除权重因子与松弛因子后，可得到如下等式：

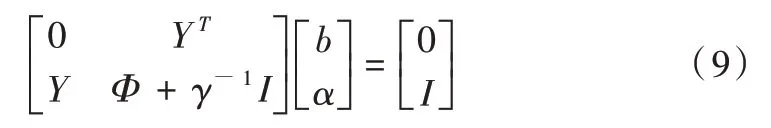
式中，Φ=ZZT为n × n单位矩阵，结合式（8）、式（9），可得到：

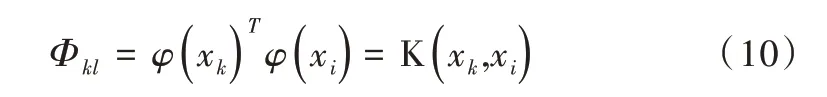
其中，K(xk,xi)是核函数。上式用核函数形式来表现，则：

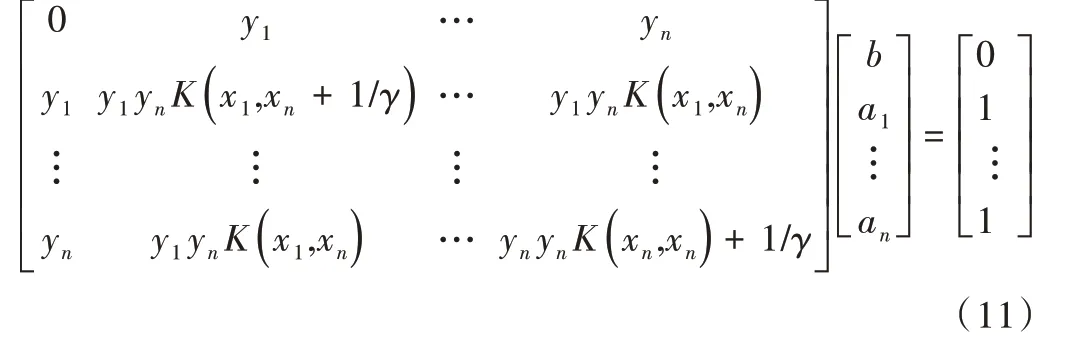
至此，可得到最小二乘支持向量机（LSSVR）模型为：

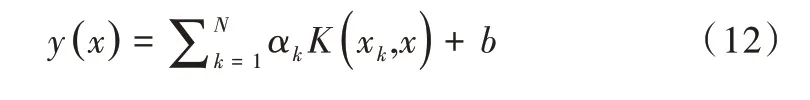
在该LSSVR 模型中，最重要的两个参数分别为正则化参数（gam）与核函数参数（sig2）。

2 RBF 神经网络

人工神经网络可通过网络进行学习与训练，不断调整权值和阈值，利用非线性函数将输入的数据映射到高维空间，加权后输出最终结果［14-15］。典型的神经元结构由3 层组成，具体神经元模型如图1 所示。

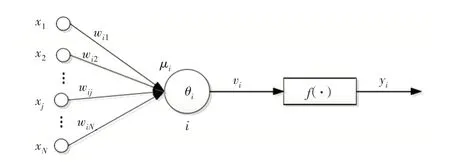
Fig.1 Neural net model图1 神经元模型

在神经元模型中，xj,j=1,2,…N为输入层输入数据，wij为连接权重，θi为第i 个神经元阈值，f(·)代表激励函数，yi代表第i 个神经元的输出值。

将径向基函数引入神经网络，建立径向基神经网络（RBF），使得神经网络具有更好的泛化能力及更快的收敛速度。RBF 神经网络结构如图2 所示［16］。

Fig.2 RBF nueral network图2 RBF 神经网络

在模型中，数据条件属性的维数决定了输入层节点个数，预测目标值则通过一个输出层节点进行输出。满足径向基函数特性的函数有3 个，具体公式如下［17-18］：

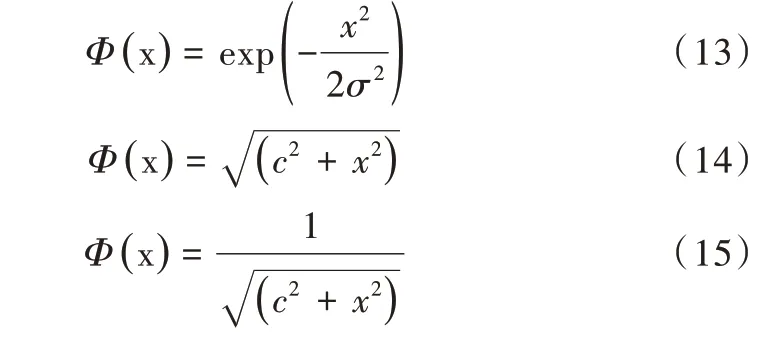
将高斯函数引入径向基函数后，其表现形式为［19］：

其中，N 表示隐藏层个数，ci表示第i个隐藏层节点中心向量，σi表示第i 个隐藏层节点半径，连接权重W 为：

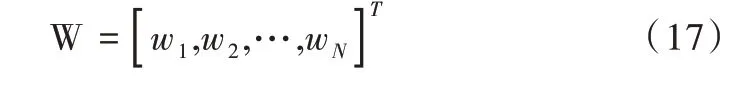
则RBF 网络输出y 可表示为：

以上3 个参数ci、σi、wi常采用梯度下降法进行优化。

RFB 的优化目标函数为［20］：

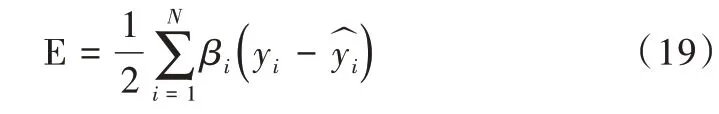
βi表示遗忘因子，yi表示实际值，为预测值。E对ci、σi、wi的偏导数为：

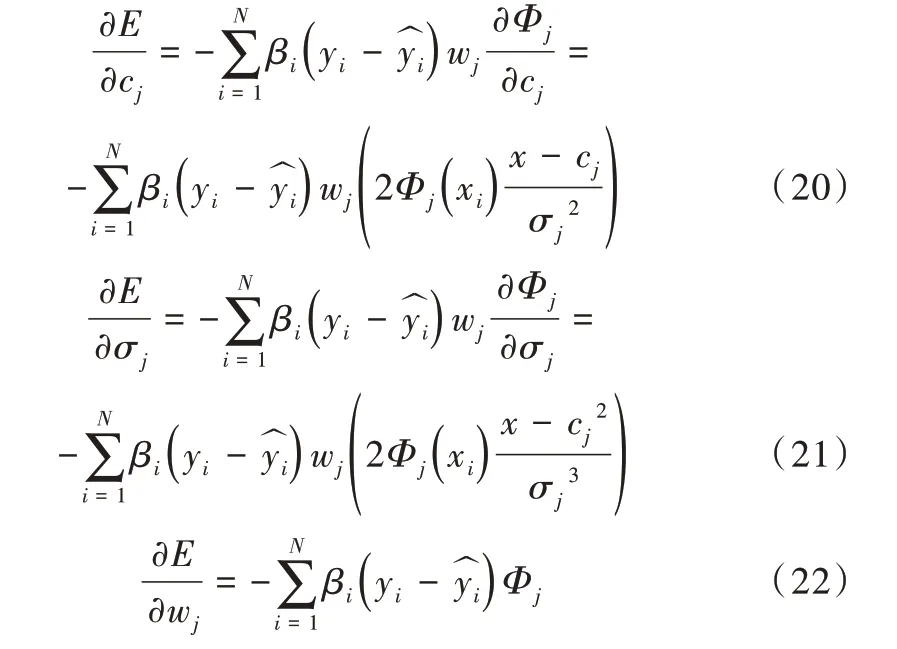
ci、σi、wi根据以上公式不断进行训练并循环调整，使网络预测值达到期望值。

3 混合回归预测模型

式中，yi表示实际值，Δi表示误差项。本文尝试使用粒子群算法与最小二乘支持向量机的混合回归预测算法，从Δi中提取未被学习与利用的有效信息，以进一步提高回归预测模型精度。

假设训练与测试数据集具有相似的误差，则可使用测试数据集误差的估计值对支持向量机预测值进行修正，具体公式如下：

为避免f(Xi)出现过拟合或欠拟合的情况，本文使用改进的粒子群算法对最小二乘支持向量机的两个关键参数——正则化参数（gam）与核函数参数（sig2）进行优化。

3.1 粒子群算法及其优化

粒子群算法中每一个粒子具有两个重要特征值，即全局最优值与局部最优值，由这些粒子组成的粒子群可在搜索空间中搜索最优位置。

在n 维空间中，第i 个粒子经过k 次迭代后，其位置Xi(k)与速度Vi(k)为：

则在第k+1 次迭代时，粒子的位置和速度可表示为：

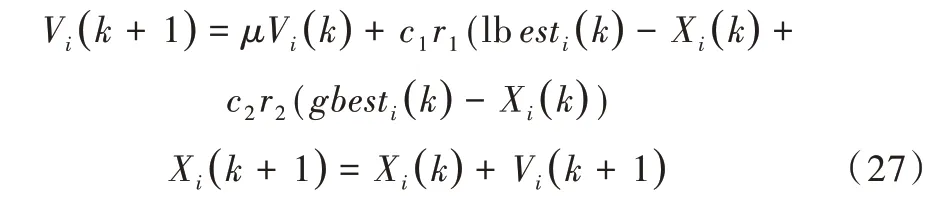
其中，r1、r2为[0,1]的随机数，c1、c2为学习因子，μ为惯性权重。

由于惯性权重μ对全局搜索与局部搜索能力的平衡具有重要影响，可避免粒子群算法陷入局部最优，因此本文采用动态调整公式对惯性权重μ进行优化：

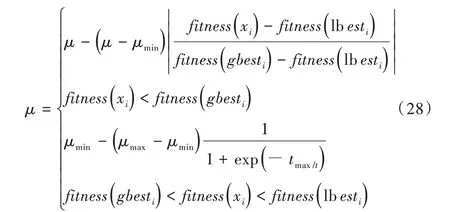
式中，μmax表示惯性权重最大值，μmin表示惯性权重最小值，tmax表示最大迭代次数。

粒子群算法优化过程如图3 所示。

3.2 混合回归预测模型构建与预测

因为支持向量机训练产生的残差值Δi与训练集的条件属性具有关联性，所以可将两者结合为新的训练数据集来训练RBF 神经网络模型，使RBF 神经网络能够进一步提取Δi中未被利用的信息，从而提高支持向量机预测精度。LSSVM-RBF 算法流程如图4 所示。

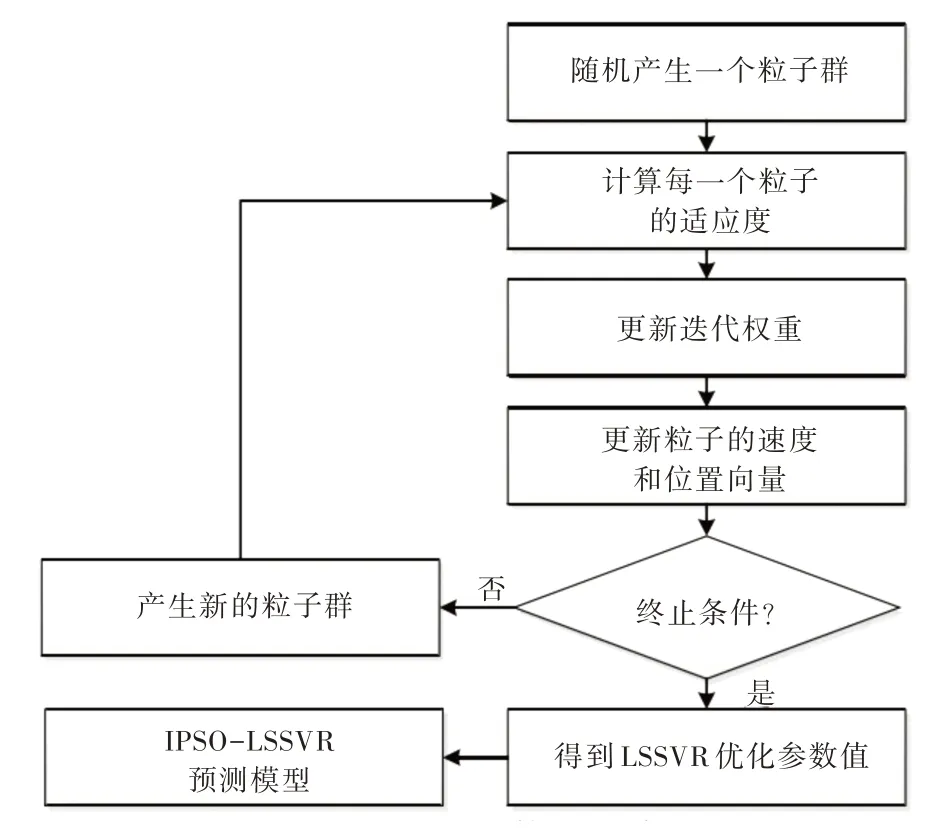
Fig.3 Particle swarm algorithm optimization process图3 粒子群算法优化过程

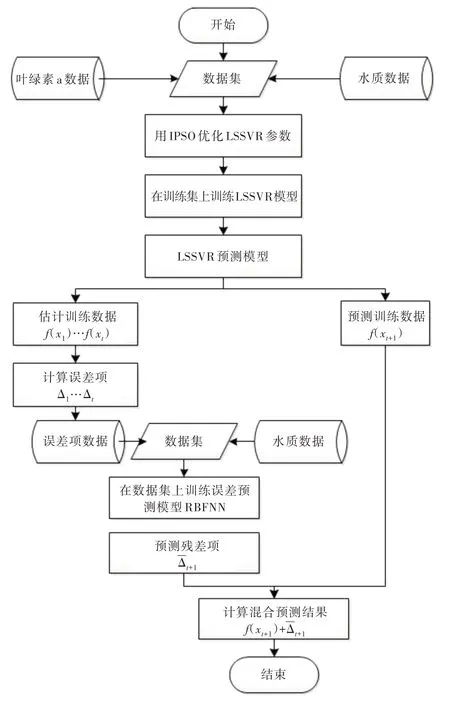
Fig.4 LSSVM-RBF algorithm flow图4 LSSVM-RBF 算法流程

在以上算法流程基础上，可构建基于最小二乘向量机与粒子群优化RBF 神经网络的混合回归预测模型。利用该模型对估计值与残差进行预测。具体步骤如下：

（1）根据图3 的算法优化过程，采用改进的粒子群算法对LSSVR 参数进行优化。

4 实验分析

在流域生态环境趋势预测中，其中的水环境预测十分重要。根据文献［20］的研究，水中叶绿素a 的浓度高低可体现水质富营养化程度。本文采用混合回归预测模型，通过对水中叶绿素a 的浓度预测，以更好地了解该流域的水生态环境趋势，并选取总磷（TP）、总氮（TN）、PH 值、高锰酸盐（CODmn）、溶解氧（DO）几个与叶绿素a 相关的条件属性。

为了对结果进行客观评价，选取4 个常用模型进行对比，包括：RBF 神经网络模型、ϵ-SVR模型、LSSVR 模型、IPSO-LSSVR 模型。经过数据集训练后，各模型预测误差如表1 所示。叶绿素a 浓度预测值如图5 所示。