气-面相互作用对均匀加热微梁系统中稀薄气体流动特性影响的数值研究

王晓伟，武 越，杜春林，韩 峰，张志军*，张世伟

（1. 东北大学 机械工程与自动化学院，沈阳 110819； 2. 北京卫星环境工程研究所，北京 100094）

0 引言

在没有任何初始压力梯度的稀薄气体中，非均匀温度场会诱导气体流动，且浸没在气体中的结构会受到辐射力[1-3]。该现象最早发现于19 世纪后期William Crookes 爵士发明的辐射计中[4]。该辐射计由安装在抽真空的玻璃灯泡内部的一组薄叶片组成，叶片一面涂成黑色，另一面为光亮的白色。将该装置放置于阳光下，叶片开始旋转，旋转方向为从黑色一面指向白色一面。

随着航空航天科学技术和微机电系统（MEMS）的发展，研究人员对应用辐射力的兴趣日益浓厚。Jones 异想天开地提出基于辐射力的直升机[5]和微型巡航导弹[6]。基于辐射力的推进系统还可用在临近空间飞行器上[7]，由安装在航天器表面的多个方形叶片阵列为航天器提供升力或者阻力补偿力。研究发现，在40～80 km 的高度上，这种推进系统叶片上的辐射力能够达到25 mN/m2。此外，由于对环境压力、温度以及气体成分较为敏感，辐射力也被用于MEMS 传感器中的压力测量[8]和气体检测[9-20]。

最近，Strongrich 等[9-10]提出一种基于辐射力驱动的设备（Microelectromechanical In-plane Knudsen Radiometric Actuator, MIKRA），可用于气体检测。研究表明，物理和几何参数显著影响该设备的性能[21-22]：当冷热微梁温差从10 K 增大到100 K 时，最大辐射力将增大7 倍以上；辐射力随环境压力的增大呈现出“钟形”分布规律；微梁宽度的增大将使设备整体所受辐射力减小，且最大辐射力在更小的环境压力下取得；微梁高度增大3 倍时，最大辐射力将增大3.66 倍；当梁的高度与宽度的比值增加9 倍时，最大辐射力能增大5.33 倍。需要指出的是，在这些研究中气体与所有梁表面之间的相互作用规律都是基于完全漫反射假设；然而，在实际应用中这种假设并非总是成立的。有关研究表明，气-面相互作用规律（表面调节系数）对流场结构、传热特性、压力分布以及辐射力都有显著的影响[23-25]。Zhou 等的研究表明[23]，法向能量调节系数（NEAC）和切向动量调节系数（TMAC）对微通道内的压力分布和流场结构会产生很大的影响；并且，相比于NEAC，改变TMAC 对流动特性的影响更为显著。此外，Kalempa 和Wang 等[24-25]研究了气-面相互作用规律对稀薄气体中球体和微梁周围流体特性的影响，发现对于辐射力，改变NEAC 和TMAC 会产生相反的作用。值得注意的是，在文献[25]的研究中，微梁（一对冷热梁）上的NEAC 和TMAC 是同步变化的，并没有考虑其中一根梁上表面调节系数单独变化的影响情况。

为了补充气-面相互作用规律对辐射力影响的理论研究，本文采用直接模拟蒙特卡罗（DSMC）方法研究微梁周围的稀薄气体流动特性，主要考查过渡流态下单梁表面调节系数变化对流场结构、传热特性、压力分布以及辐射力等的影响，以期为相关器件的设计制造和应用提供理论参考与指导。

1 气-面相互作用模型

常见的气-面相互作用模型包括镜面反射、漫反射、Maxwell 以及CL（Cercignani-Lampis）模型。对于不同的气-面相互作用模型，气体分子撞击壁面并发生反射的速度分布规律[26]如图1 所示。镜面反射模型是最简单的气-面相互作用模型，它假设撞击到表面的气体分子类似于完全弹性的球体一样被反射，即，气体分子的法向速度分量反向而切向速度分量保持不变，如图1(a)所示，这意味着在这种气-面相互作用过程中，气体分子与壁面之间不发生热传递和摩擦行为。对于漫反射模型，撞击到壁面的气体分子首先与表面进行能量交换，使气体分子温度和壁面温度达到热平衡；然后根据由壁面温度确定的半范围Maxwell 分布，随机分配反射分子的速度，如图1(b)所示。前面这2 种气-面相互作用模型都不太切合实际，因此出现了Maxwell模型。实际上，Maxwell 模型是漫反射与镜面反射模型的组合[27]，在模型中引入调节系数α（0≤α≤1）来指定入射分子在壁面上的反射形式，即，入射分子的α部分为漫反射，剩余的(1-α)部分为镜面反射。相比于Maxwell 模型，CL 模型能更真实地反映物理现实中反射分子的速度和能量分布[28]，如图1(c)所示。该模型包括2 个表面调节系数（NEAC和TMAC），二者相互独立，对于一般的光滑表面，这2 个调节系数的数值均在0～1 之间变化。本研究的所有DSMC 模拟中，气-面相互作用模型均选用CL 模型。

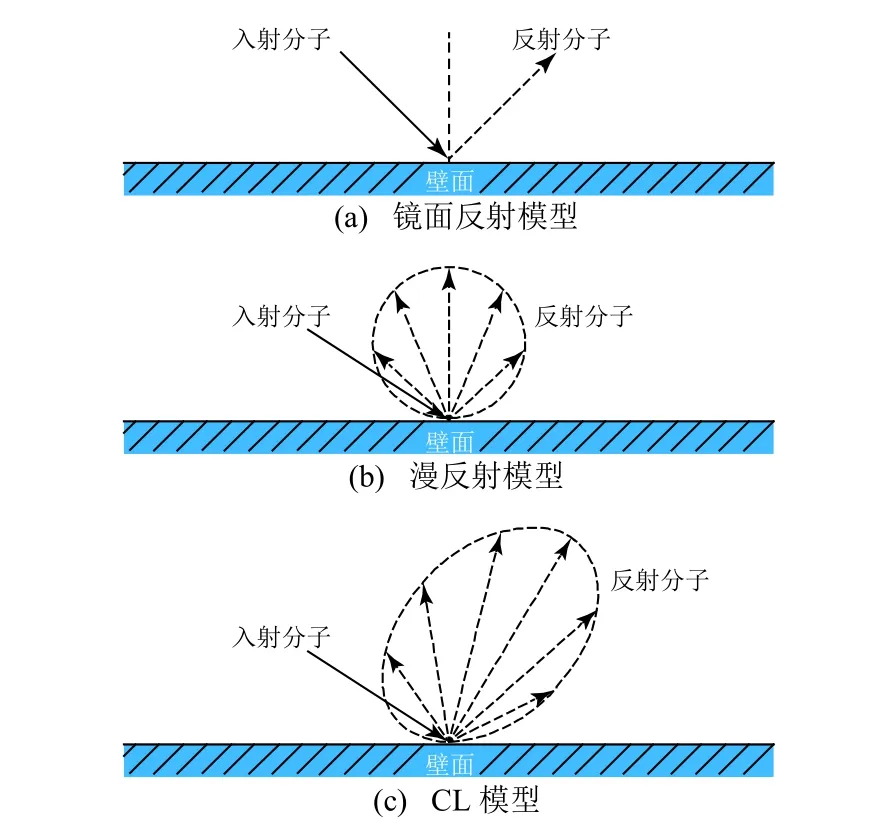
图1 不同气-面相互作用模型中反射分子的速度分布示意Fig. 1 Schematics diagram of velocity distributions of reflected molecules based on different gas-surface interaction models

2 问题陈述与数值方法

由于MIKRA 设备中冷热梁的长度（1.4 mm）远大于其横截面尺寸（50 μm×50 μm），所以只需进行二维模拟以近似表征实际的气体流动情况，模拟域如图2 所示。左右两表面为对称边界，上方是自由流边界以表征H2-N2混合气体的流入或流出，下方为基底壁面边界。冷热梁悬浮于距基底上方4 μm处。冷梁和热梁具有相同的尺寸，且在模拟过程中假设两者的间距g保持不变，为20 μm。此间距也用于计算Knudsen 数（Kn）。

图2 模拟域和边界条件Fig. 2 Simulation domain and boundary conditions

DSMC 方法基于粒子求解Boltzmann 方程[29]，使用大量的模拟粒子再现实际气体分子的运动情况，跟踪并记录这些粒子的位置、速度和内能等信息，最后对模拟粒子的微观值进行平均从而获得宏观量。该方法为了降低统计误差，需要较长的模拟时间。本文使用开源的DSMC 求解器dsmcFoam-Plus[30]来模拟微梁周围的气体流动；采用无时间计数器（NTC）方案选取粒子碰撞对；另外，因为模拟域气体介质是50%H2+50%N2的双原子混合气体[13,18,25]，所以采用变径软球（VSS）模型和Larsen-Borgnakke 模型分别模拟粒子间的碰撞和粒子本身动能与内能的交换过程。

所有模拟均在环境压力P=387 Pa（Kn=0.74）的气氛中进行；冷梁和均匀加热的热梁的温度分别为Tc=304 K 和Th=341.5 K。值得一提的是，这2 个温度是通过在纯N2气氛中将相应压力条件下测得的实验数据[9-10]取平均值得到的。根据这些参数，使用Δx=Δy=2 μm 的网格均匀地划分模拟域[10,13,18,25]，每个网格中的模拟粒子数不少于20 个。模拟计算的时间步长Δt=1 ns，总模拟时间不短于5 ms[10,13,18,25]；另外，对于表面调节系数 NEAC（αn）和TMAC（σt）均独立设为0.2、0.4、0.6、0.8 和1。本研究中只单独改变冷梁的表面调节系数，而热梁的表面调节系数恒为1（对于冷、热梁同步变化的情况，请参见文献[25]）。在物理实际中，可通过改变制造冷梁和热梁所用的材料来实现其表面调节系数的调整。本文为区分冷梁和热梁的表面调节系数，分别以上标Cold 和Hot 予以标记。

3 结果与讨论

3.1 流场结构

图3 不同NEAC 下的速度流线和温度分布云图Fig. 3 Velocity streamlines and temperature contours for different NEACs (In each of the sub-figures, the left half shows the results of αnCold=αn, αnHot=1, the right half shows the results extracted from Ref. [25], αnCold=αnHot=αn)

TMAC 变化对微梁附近流场的影响如图4 所示，同样在每幅图中均给出了本文和文献[25]的模拟结果。不难看出，相比于NEAC 对流场结构的影响，切向TMAC 的影响力较弱，且在仅改变冷梁TMAC 以及冷梁和热梁TMAC 同步变化的情况中均是如此。这一结果对微梁制作材料的选取具有一定的指导意义。同样由于热梁TMAC 的降低导致气体与壁面交换的能量减少，使得冷梁和热梁TMAC 同步改变所引起的流场结构的变化比仅改变冷梁TMAC 的情况更为明显，且流场温度更高。

图4 不同TMAC 下的速度流线和温度分布云图Fig. 4 Velocity streamlines and temperature contours for different TMACs (In each of the sub-figures, the left half shows the results of =σt, =1, the right half shows the results extracted from Ref. [25], ==σt)

3.2 传热特性

不同NEAC 对冷梁各表面传热量的影响如图5所示，每幅图中虚线数据为文献[25]的模拟结果，下同。传热量数值为正表示该表面处于吸热状态，为负则表示其处于放热状态。可以看到，受到高温热梁的影响，冷梁的上表面和右表面处于吸热状态；对于下表面，由于其温度比底部基底的更高且距离较近，故处于放热状态；左表面处于放热状态的原因是，其远离热梁且表面温度比其周围气体的温度高。正如预期的那样，NEAC 的减小导致表面传热量的绝对值减小，即，表面的吸热或放热能力减弱。另外，对于仅改变冷梁的NEAC 的情况，表面的吸热或放热能力比冷梁和热梁的NEAC 同步变化时更强。由于冷梁右表面距离热梁较近，这种现象尤为明显，如图5(d)所示。

图5 不同NEAC 对冷梁各表面传热量的影响Fig. 5 Heat transfer distributions along surfaces of cold beam with different NEACs (In each of the sub-figures, dashed lines show the results extracted from Ref. [25])

不同TMAC 对冷梁各表面传热量的影响如图6所示。可以看出，各表面的吸热或放热状态以及传热分布规律与改变NEAC 时的一致。从传热量上来看，改变TMAC 比改变NEAC 能够获得更大的绝对值。

图6 不同TMAC 对冷梁各表面传热量的影响Fig. 6 Heat transfer distributions along surfaces of cold beam with different TMACs (In each of the sub-figures, dashed lines show the results extracted from Ref. [25])

这对于物理应用中的热管理具有一定的参考价值，即，针对材料不同的微梁需要配备不同换热能力的散热系统。另外，仅改变冷梁的TMAC 获得的结果与冷梁和热梁的TMAC 同步变化所得到的结果之间的差异在TMAC 较大的情况下并不明显，只在TMAC 较小时才能凸显。

3.3 压力分布特性

图7(a)和图7(b)分别为NEAC 和TMAC 变化对冷梁左右表面压力分布的影响。

图7 不同表面调节系数下冷梁左右表面的压力分布Fig. 7 Pressure distributions along left and right surfaces of the cold beam with different surface accommodation coefficients (In each of the sub-figures, dashed lines show the results extracted from Ref. [25])

由图7(a)可以看到，仅改变冷梁的NEAC 在引起梁表面压力变化方面与冷梁和热梁的NEAC 同步变化的情况显示出完全不同的结果。更确切地说，如果仅仅改变冷梁的NEAC，冷梁右表面压力始终大于左表面压力，且随着NEAC 的减小，右表面压力明显增大。这意味着冷梁与热梁两者之间相互排斥。而对于冷梁和热梁NEAC 同步变化的情况，则会出现冷梁左表面压力大于右表面压力的现象，且随着NEAC 的降低右表面压力明显减小，这种现象更为显著[25]。这意味着冷梁与热梁两者之间在NEAC 较大时是相互排斥的，而当NEAC 较小时则表现为相互吸引。因此，在物理实际中可通过选用不同的材料来实现对微梁移动方向的控制。

由图7(b)可以看到，无论是仅改变冷梁的TMAC还是同步改变冷梁和热梁的TMAC，冷梁右表面压力均始终大于左表面压力，即，冷梁与热梁两者之间相互排斥。此外，随着TMAC 的减小，右表面压力明显增大，且同步降低冷梁和热梁的TMAC 在增大右表面压力方面比仅降低冷梁的TMAC 的情况表现出更显著的效果。

3.4 辐射力

在DSMC 中，施加在冷梁上的辐射力F可通过撞击在冷梁表面的入射粒子和反射粒子之间的动量变化来计算，

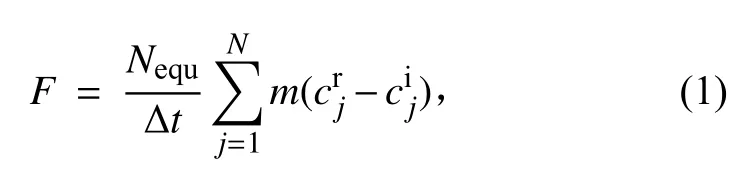
式中：Nequ为一个DSMC 模拟粒子所代表的真实气体分子数量；N为与表面相互作用的总粒子数；m为粒子的质量；c为粒子的速度，上标i 和r 分别表示入射粒子和反射粒子。

图8(a)和图8(b)分别为NEAC 和TMAC 变化对冷梁所受辐射力的影响，其中虚线为文献[25]的结果。

由图8(a)可以看出，对于仅改变冷梁的NEAC与冷梁和热梁的NEAC 同步变化这2 种情况，冷梁所受辐射力对NEAC 的依赖性显示出完全不同的情形。更确切地说，如果同步减小冷梁和热梁的NEAC，辐射力随着NEAC 的减小呈非线性减小，当αn＜0.2 之后出现辐射力方向反转的现象，且其绝对值具有随着NEAC 的减小而增大的趋势（辐射力曲线的斜率随着NEAC 的减小而增大）；而对于仅减小冷梁的NEAC 的情况，辐射力随着NEAC的减小呈近似线性增大。

由图8(b)可以看出，在仅改变冷梁表面TMAC的情况中，辐射力随着TMAC 的减小呈非线性减小；而对于冷梁和热梁的TMAC 同步变化的情况，辐射力却随着TMAC 的减小呈非线性增大。同时，我们注意到，在这2 种情况中，随着TMAC 的减小辐射力曲线的斜率（绝对值）均增大。

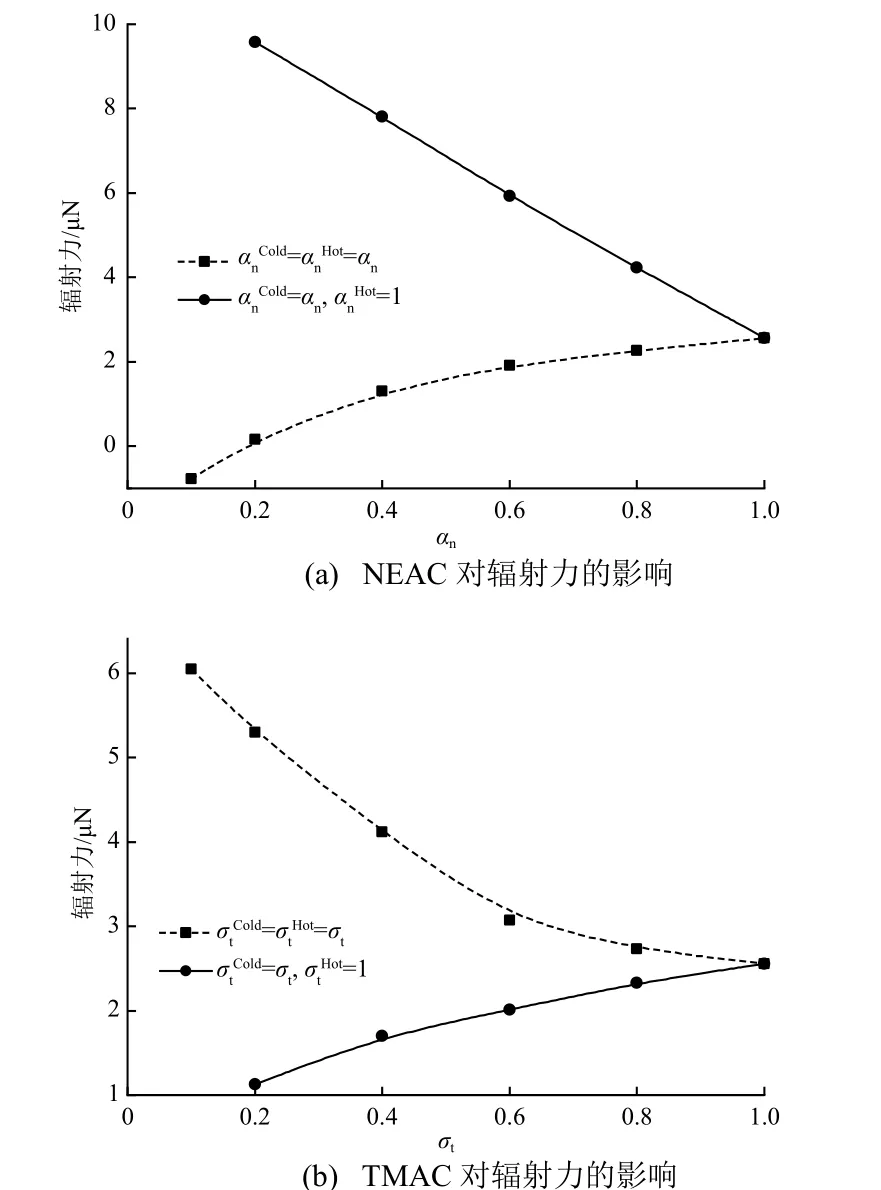
图8 不同表面调节系数下冷梁所受辐射力Fig. 8 Radiometric force of the cold beam with different surface accommodation coefficients (In each of the sub-figures, dashed lines show the results extracted from Ref. [25])

4 结束语

本文采用DSMC 方法并基于CL 气-面相互作用模型研究法向能量调节系数（NEAC）和切向动量调节系数（TMAC）对一组微梁周围稀薄气体流动的影响。结果表明，表面调节系数对流场结构、传热特性、压力分布和辐射力的影响是显著的。为了在实际应用中尽可能地获得最大的辐射力，在设计和制造MEMS 器件时，如果冷梁和热梁使用相同的材料，则应该选取NEAC 较大而TMAC 较小的材料；如果冷梁和热梁使用不同的材料，则冷梁应该选具有较小NEAC 和较大TMAC 的材料，而热梁应该选NEAC 和TMAC 均较大（最好接近于1）的材料。