球形弹丸超高速斜撞击薄板的碎片云和侵彻特征仿真分析

2022-01-07邓勇军

航天器环境工程 2021年6期

刘昕，邓勇军,2*，彭芸，姚勇,2

（1. 西南科技大学土木工程与建筑学院； 2. 工程材料与结构冲击振动四川省重点实验室：绵阳 621000）

0 引言

自20 世纪以来，人类航天活动日益频繁，造成空间碎片数量急剧增加。空间碎片与航天器发生碰撞时的速度可能高达10 km/s，会造成航天器机械损伤乃至功能失效，给航天器安全和航天员生命带来极大威胁的同时也蕴含着重大任务风险和经济损失。

对于超高速斜撞击的首次研究可追溯到20 世纪50 年代[1]。随后有实验表明，斜向超高速撞击产生的碎片云与正撞击产生的碎片云有很大区别[2]；碎片云性质与弹丸尺寸有密切关系[3]。Schonberg 等[4-6]研究了弹丸超高速斜撞击中的跳弹现象以及空间分布，发现法向碎片云和轴向碎片云是跳弹碎片云的派生，并基于物理冲击条件建立了斜撞击冲击波的分析模型。

当前，在超高速斜撞击研究中，靶板主要使用延性材料，对脆性材料[7-9]和复合材料[10-11]的研究相对较少。对于撞击特征的研究主要基于经验分析，以穿孔经验公式[12-15]为主，也有关于碎片云特征尺寸参量与撞击角度、速度和弹丸直径的经验公式[16-17]。

研究表明，撞击所产生的碎片云分布对于防护结构后板的损伤特性有着重要的影响：其尺寸和投影面积会受到撞击角度的影响[18-19]，同时存在产生多弹坑的临界冲击角[20]；靶板厚度/弹丸直径（t/d）在很大程度上决定了碎片破坏的阈值冲击速度以及碎片云的尺寸分布[21-22]。此外，撞击时界面温度[23]、弹丸材料组成[24]、t/d值[25]对铝合金弹丸撞击铝合金目标时的破片尺寸分布亦有影响。Piekutowski[26]研究了大碎片的等效直径与弹丸直径的比例关系，并且和t/d的影响结果进行比较。Verma 等[27]用无量纲经验方程来评估碎片云中的最大碎片对于防护结构的损伤能力。最近的研究基于数值模拟可以得到碎片云的特征点速度和边界[28]，详细量化了危险碎片的集中区域，为防护结构的损伤提供了一种量化评估方法[29]。Wen 等提出了一种利用椭圆函数描述冲击波的几何传播模型[30-31]，为后续的弹丸破碎[32]和失效演化[33]的分析和量化提供了理论基础。总的来说，目前对于撞击速度在7 km/s 以下的实验研究较为充分，但对更高速度的球形弹丸的撞击研究相对缺乏，主要受限于实验发射能力，且还需要考虑相变、电离等现象，在数值模拟中须重点解决的问题是要有能够描述相变现象的状态方程[34-35]。

上述学者的研究大多基于地面实验，然地面实验成本高、准备周期长、限制条件多，且弹丸与前板作用时间极短、反应剧烈，当前的实验技术难以对该过程进行直接观察。相比而言，数值模拟计算具有快速、直观的特点，不仅能弥补实验研究之不足、处理实验无法解决的工况，还能为实验提供指导，更充分地了解撞击的全过程以及超高速撞击现象的内在机理。计算采用的撞击弹丸多选择球形弹丸，因为球形结构完全对称，只需要一个尺寸参数即可描述，不存在撞击姿态的问题，便于分析和比较。

本文基于光滑粒子流体动力学（smoothed particle hydrodynamics, SPH）方法，利用Autodyn-3D 软件对球形弹丸超高速斜撞击薄板进行模拟，通过算例分析找出撞击速度、撞击角度对于碎片云形貌和几何尺寸，以及穿孔大小和形状的影响规律，旨在模拟出航天器舱壁与空间碎片超高速斜碰撞的情况，为后续的防护设计工作提供支持。

1 模型算法

弹丸材料为Al2017-T4，直径6 mm；靶板薄板材料为Al2A12，尺寸为50 mm×50 mm，厚度为0.5 mm。弹丸和薄板均采用SPH 算法建模，粒子大小0.1 mm，排列方式均为矩形排列[36]。数值计算模型如图1 所示，为节省计算时间，采用3D 轴对称方式建模：正撞击工况采用1/4 对称建模；斜撞击工况采用1/2对称建模。计算时间步长为20 μs。

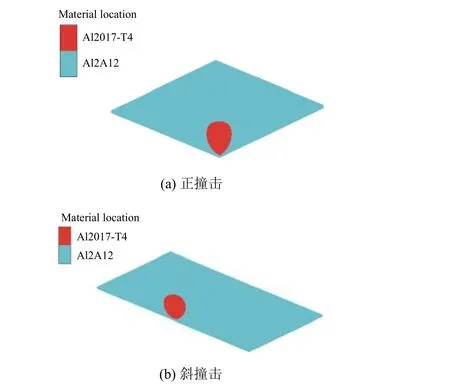
图1 弹丸撞击薄板的数值计算模型Fig. 1 Numerical model of spherical projectile impact on thin plate

1.1 状态方程

在1 kPa 压力范围[29]内，对晶体材料来说，Mie-Grüneisen 状态方程较为常用。由于冲击绝热关系与高压固体状态方程之间联系密切，而冲击绝热关系的实验数据较多，所以Mie-Grüneisen 状态方程可以通过冲击绝热关系确定，其定义为

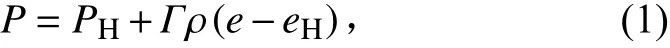
式中：P和e分别为静水压力和比内能；PH和eH分别为冲击Hugoniot 曲线上静水压力和比内能的参考值；Γ和ρ分别为材料的Grüneisen 参数和密度，Γρ=Γ0ρ0=常数，相应的Γ0和ρ0为材料的初始Grüneisen 参数和初始密度。常用的“shock”形式Mie-Grüneisen 状态方程的定义为

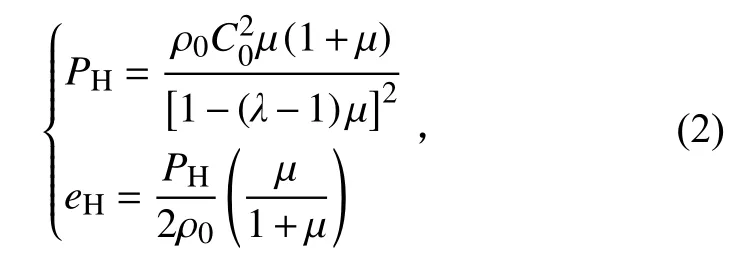
式中：μ=ρ/ρ0-1；λ为冲击波速度U与波后质点速度up之间线性关系的斜率，通常U=C0+λup，C0为体积声速。Al2017-T4 和Al2A12 的Mie-Grüneisen 状态方程参数见表1[36]，其中S为输入常数。

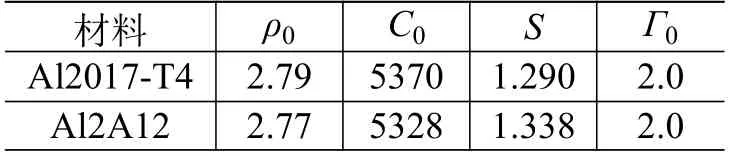
表1 Mie-Grüneisen 状态方程参数[36]Table 1 Parameters of Mie-Grüneisen equation of state[36]

1.2 强度模型

Johnson-Cook 模型与Steinberg-Guinan 模型是2 种常用的材料强度模型[36]。

Johnson-Cook 模型能够反映应变率强化效应和温度软化效应，在超高速撞击数值模拟中较为常用，其屈服应力σ的表达式为

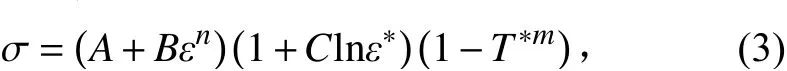
式中：ε为等效塑性应变；ε∗=ε˙/ε˙0，为相对等效塑性应变率，其中参考应变率ε˙0=1 s-1；T*=(T-Troom)/(Tmelt-Troom)，其中，Troom为室温，Tmelt为熔点温度；A、B、C、m和n均为材料参数，其中，A为材料在准静态下的屈服强度，B和n表征应变硬化的影响，C为应变率敏感系数，m为温度软化系数[36]。Al2017-T4的Johnson-Cook 强度模型参数见表2[36-37]。

表2 Al2017-T4 的Johnson-Cook 强度模型参数[36-37]Table 2 Parameters of Johnson-Cook strength model for Al2017-T4[36-37]

Steinberg-Guinan 屈服模型定义剪切模量G和屈服应力Y为

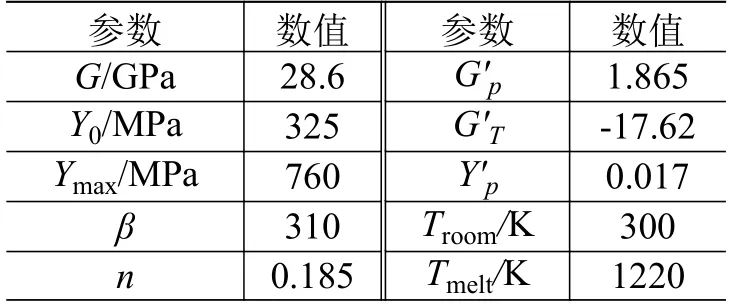
表3 Al2A12 的Steinberg-Guinan 强度模型参数[36]Table 3 Parameters of Steinberg-Guinan strength model for Al2A12[36]

1.3 失效模型

材料不可能承受任意大的拉伸应力，需要定义失效模型来描述材料的极限强度与失效形式，特别是在超高速撞击条件下，必须考虑弹丸与薄板材料的失效问题。常用的材料失效判据有应力判据和应变判据2 种，本文在模拟计算中采用应力失效判据，即认为：当材料所受最大拉应力超过材料的失效应力时材料失效，不再承受拉应力。邸德宁等[38]通过考查不同失效模型（无失效模型、Grady 失效模型和最大拉应力失效模型）下计算出的碎片云外形尺寸及速度、粒子点失效表现和碎片数量分布，发现Grady 失效模型更符合实验结果。Grady-Spall失效模型认为，在确定的失效应变εc下，失效应力σs随着材料密度ρ、体积声速C0以及屈服应力Y等的变化而变化。对于承受冲击荷载的韧性材料，其失效应力为

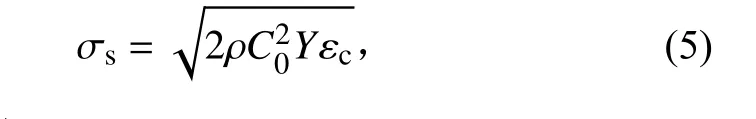
铝合金材料的εc=0.15。

1.4 数值模拟准确性验证

为验证数值模拟的准确性，将数值模拟结果与地面实验结果（文献[36]中的05 工况）进行比较。如图2 所示，当撞击速度为5 km/s 时，7.02 μs 时刻两者的碎片云形态大致相同。在建立数值模型时提前设置高斯点读取各个时刻、位置的速度，取其中2 个特征点速度（v1a、v2a）与地面实验结果进行比较，结果如表4 所示，数值模型与实验结果间的相对误差不超过5%，说明二者吻合较好。

图2 地面实验[36]与数值模拟结果的比较（撞击速度：5 km/s；时刻：7.02 μs）Fig. 2 Comparison between the results of ground experiment[36] and numerical simulation(impact velocity: 5 km/s; time: 7.02 μs)

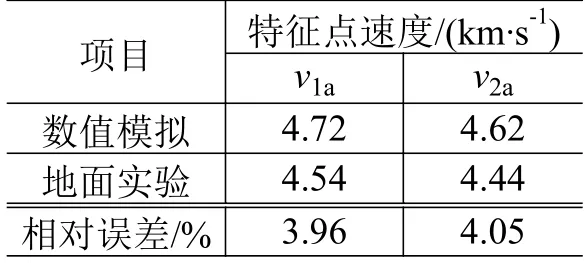
表4 特征点的速度比较Table 4 Comparison of the speeds at characteristic points

2 碎片云形成机理

2.1 碎片云的组成

如图3(a)所示，正撞击中，碎片云结构包括反溅碎片云、外泡碎片云以及内核碎片云（即主体碎片云和后剥落碎片云）。反溅碎片云是高速撞击过程中产生的向薄板前方喷射的大量小碎片的组合，主要由薄板材料组成；外泡碎片云是一个由大量碎片膨胀形成的封闭结构，主要由薄板材料组成，也包含一小部分弹丸材料；内核碎片云由弹丸破碎形成，位于外泡碎片云内部的前方，占整个碎片云质量的大部分；后剥落碎片云是由弹丸后表面一定厚度的材料破碎、剥落形成。

如图3(b)所示，斜撞击中，形成了3 种不同的碎片云：其中，薄板后方的碎片云可以根据其运动方向细分为2 种，在较小的撞击角度下，几乎无法区分它们；随着撞击角度θ的增大，可以看到其中一部分碎片云朝着撞击速度的方向移动，而另一部分则朝着薄板的法线方向移动，故将它们分别称为轴向碎片云和法向碎片云。轴向碎片云主要为弹丸碎片，而法向碎片云主要为薄板碎片。第3 种碎片云称为跳弹碎片云，出现在薄板前方，设弹丸碎片发生反溅的临界撞击角为θc，即当θ＜θc时弹丸碎片不会发生滑弹反溅，θ≥θc时则发生滑弹反溅。发生滑弹反溅时，只有部分弹丸碎片穿过靶板，与靶板碎片形成透射碎片云，而其余碎片则发生滑弹，形成滑弹反溅碎片云[14]。

图3 超高速撞击碎片云结构示意[27,36]Fig. 3 Sketch of debrisclouds’ structure in hypervelocityimpact[27,36]

2.2 应力波分析

虽然球形弹丸形状规则，不存在撞击姿态问题，但其与前板的撞击面不是平面，将导致冲击波在弹丸表面的反射和波系的空间传播及衰减呈高度非线性。

以球形弹丸SD6（直径6 mm）为例，撞击速度为5 km/s，撞击角度分别为0°和45°的情况下分析碎片云形成过程，弹靶内部的应力波变化如图4所示。

图4 超高速正、45°斜撞击下弹靶内部各个时刻应力波的变化Fig. 4 Variation of stress waves inside a projectile target at various moments under hypervelocity forward and oblique(45°) impacts

正撞击（见图4(a)）下，在t=0.05 μs 时刻，弹丸与薄板一接触就立即在材料内部产生冲击波，并在弹丸和薄板内部反向传播。在t=0.20 μs 时刻，薄板的压缩波较早到达薄板背面反射成为拉伸波并向弹丸方向传播。在t=0.50 μs 时刻，撞击边缘处的单元首先达到失效阈值，材料破碎成碎片；接触面处的粒子在弹和板的挤压下沿接触面向后喷出，形成反溅碎片云。在t=0.70 μs 时刻，压缩波呈弧面，且曲率小于弹丸表面的曲率，因此压缩波到达弹丸表面各处的时刻不同；压缩波到达弹丸表面后反射为拉伸波，与薄板反射的拉伸波叠加后导致弹丸内部开始发生层裂；随着时间的推进，层裂碎片在其内部应力波以及碎片间相互碰撞的共同作用下使弹丸内部损伤逐渐增大，碎片数目增多、尺寸继续减小，同时薄板的鼓包逐渐增大，部分单元失效，形成环状的碎片。

45°斜撞击（见图4(b)）相较于正撞击，同一时刻下应力波在弹、板中传播得较慢，并且继续作用应力波的分布也变得不均匀，主要沿撞击速度方向分布较为明显。其原因是当弹丸的速度方向与薄板的法线方向具有一定的角度之后，与薄板作用的为速度分量，应力波的传播会受到削弱，使得弹丸和薄板内的应力波卸载得较晚，导致斜撞击的碎片云的形成时间晚于正撞击工况（对比t=0.35 μs 时刻）。

3 参数分析

3.1 撞击速度对碎片云的影响

1）碎片云形貌

图5 为不同撞击速度下的碎片云形貌。正撞击中，外泡碎片云、后剥落碎片云呈椭球形，主体碎片云呈蝶形，反溅碎片云呈上下扩散的圆台形态；随着撞击速度的增大，外泡碎片云逐渐由椭球形变为水滴形，主体碎片云破碎程度加剧，“翼缘”部分逐渐清晰且尺寸增大，后剥落碎片云体积逐渐增大，上下扩散得更远，轮廓的曲率逐渐变大。45°斜撞击中，跳弹碎片云形状不规则，并向远离撞击速度的方向膨胀；薄板前方的碎片云不再呈现蝶形；随着撞击速度的增大，弹丸材料破碎得更加彻底，并且在跳弹碎片云和轴向碎片云中分布广泛，而在法向碎片云中分布相对稀少。

图5 不同撞击速度下的碎片云形貌Fig. 5 Debris cloud morphology under different impact speeds

2）碎片云几何尺寸

以几何参数α、β、γ、δ描述碎片云的几何特征，其具体含义为：α表示轴向长度，即碎片云沿撞击速度方向膨胀的最远距离；β表示上径长度，即以撞击速度方向为轴向，碎片云上部膨胀最远处与轴向的垂直距离；γ表示下径长度，即碎片云下部膨胀最远处与轴向的垂直距离；δ表示膨胀距离，即碎片云沿靶板中垂线方向膨胀的最远距离。由图6 可以看到，正撞击中碎片云上下对称，斜撞击中碎片云上下不对称。

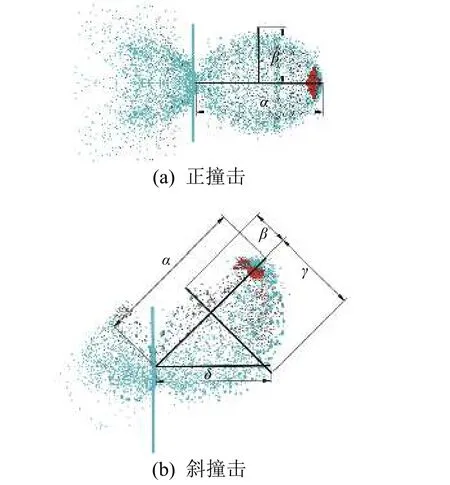
图6 碎片云几何特征参数Fig. 6 Geometric characteristic parameters of debris cloud

撞击速度对碎片云几何特征参数α和δ的影响见图7。如图7(a)所示，在正撞击和斜撞击中，碎片云轴向长度均与撞击速度近乎呈线性关系，正撞击时撞击速度对碎片云轴向长度的影响更显著。

图7 撞击速度对碎片云几何特征参数α 和δ 的影响Fig. 7 The axial length and the expansion distance of the debris cloud under different impact speeds

如图7(b)所示，撞击角度为0°～15°时，碎片云膨胀距离受撞击速度影响显著，两者间近乎呈线性关系；而当撞击角度超过30°时，膨胀距离随撞击速度的变化呈现出先减小后增大的趋势。

撞击速度对碎片云几何特征参数β和γ的影响见图8。如图8(a)、(b)所示，在正撞击和斜撞击中，上、下径长度均与撞击速度近乎呈线性关系，但在斜撞击中，撞击速度对下径长度的影响更显著。引入上、下径长度比值参数β/γ（0＜β/γ≤1）以反映碎片云形状的对称程度，该比值越小表示碎片云形状的不对称性越明显。如图8(c)所示，该参数受撞击速度的影响不明显。

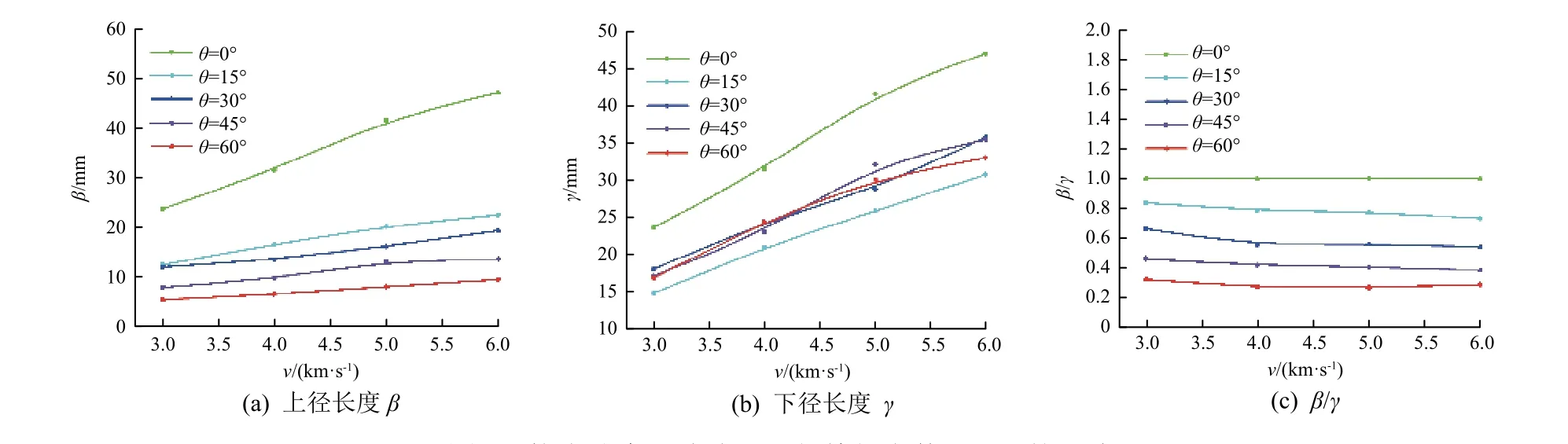
图8 撞击速度对碎片云几何特征参数β 和γ 的影响Fig. 8 The top and bottom radial diameters of the debris cloud under different impact speeds

3.2 撞击角度对碎片云的影响

1）碎片云形貌

如图9 所示，与正撞击相比，斜撞击产生的碎片云形貌具有不对称性，随着撞击角度的增大，轴向碎片云逐渐向撞击速度方向发生偏转移动，法向碎片云依然沿着薄板法向移动，并且弹体也会破碎得更加彻底。碎片云沿撞击角度一侧分布较多，会发生滑弹反溅现象，弹丸破碎的材料会进入到跳弹碎片云中，形成滑弹反溅碎片云。发生滑弹反溅现象的临界撞击角大致在30°～45°之间，并且随着撞击角度的增大，滑弹反溅的现象也越加严重，即跳弹碎片云中弹丸材料的占比会逐渐增大。

图9 不同撞击角度下的碎片云形貌Fig. 9 Debris cloud morphology for different impact angles

2）碎片云几何尺寸

如图10(a)所示，撞击角度为0°～15°时，碎片云轴向长度受撞击角度的影响显著，从正撞击工况到斜撞击工况出现骤减；但随着撞击角度的持续增大，轴向长度受撞击角度的影响逐渐趋于不明显。如图10(b)所示，与正撞击相比，斜撞击中撞击角度的偏转使得碎片云逐渐偏离薄板中垂线，因而膨胀距离随撞击角度的增大持续减小。

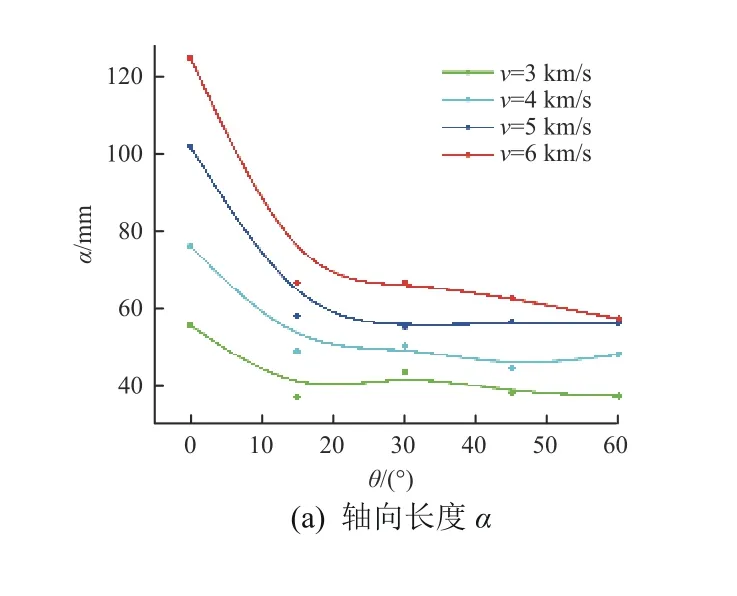
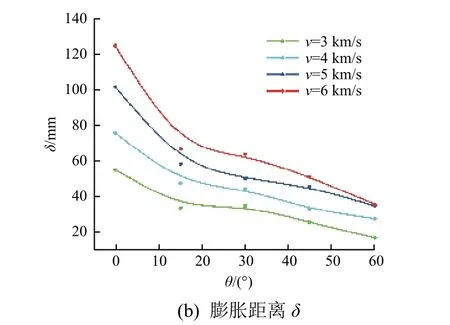
图10 撞击角度对碎片云几何特征参数α 和δ 的影响Fig. 10 The axial length and the expansion distance of the debris cloud for different impact angles

如图11(a)所示，碎片云的上径长度随着撞击角度的增大而逐渐减小。如图11(b)所示，随着撞击角度的增大，碎片云的下径长度先减小后基本保持不变。撞击角度为0°～15°时，向弹丸速度方向的偏转直接影响碎片云的分布，下径长度的下降速度最快；撞击角度为15°～60°时，下径长度几乎不受撞击角度的影响。如图11(c)所示，随着撞击角度的增大，碎片云上、下径比（β/γ）近乎呈线性减小，说明碎片云偏离薄板法线的程度受撞击角度的影响明显，碎片云形状也逐渐偏离椭球形。

图11 撞击角度对碎片云几何特征参数β 和γ 的影响Fig. 11 The top and bottom radial diameters of the debris cloud for different impact angles

3.3 薄板穿孔尺寸

球形弹丸斜撞击薄板时，穿孔尺寸特征参数随撞击角度的变化如图12 所示。其中：Dy为弹丸入射速度方向在靶板撞击面上投影的椭圆穿孔长度，称为椭圆穿孔长轴长度；Dx为垂直于Dy方向上的椭圆穿孔长度，称为椭圆穿孔短轴长度；(Dy/Dx)为穿孔的椭圆度。Dx、Dy的增大意味着穿孔尺寸的扩展，而(Dy/Dx)表征穿孔形状。

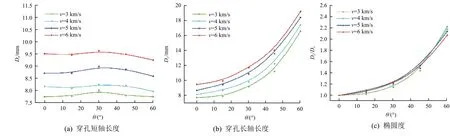
图12 穿孔尺寸特征参数随撞击角度的变化Fig. 12 The characteristic size parameters of perforation for different impact angles

如图12(a)所示，Dx随撞击角度的增大呈现先增大后减小的趋势。这是因为球形弹丸会在撞击角度增大到一定程度时发生滑弹反溅现象，且撞击角度越大，反溅碎片云中包含的弹体材料质量就越大，甚至弹丸的滑弹体积超过其投射体积，使弹丸对薄板的侵彻能力减弱，穿孔直径变小。如图12(b)所示，Dy由于与撞击速度分量方向重合，当撞击角度越大时，该速度分量就越大，越有利于Dy扩展。如图12(c)所示，穿孔的椭圆度（Dy/Dx）随撞击角度增大而增大，而撞击速度对其几乎没有影响。随撞击角度的增大，穿孔长轴尺寸的增长速度更快，而短轴尺寸的增长速度较慢，当撞击角度超过30°时，椭圆度显著增大，这是滑弹反溅造成球形弹丸的侵彻能力下降，短轴尺寸为负增长，而长轴尺寸增长变快的结果。