基于非结构化三角网格的大地电磁二维h-型自适应有限元正演模拟

乃国茹, 王绪本, 秦 策, 谢卓良, 陈先洁

(1.成都理工大学 地球物理学院，成都 610059；2.河南理工大学，焦作 454002)

0 引言

经过几代学者不懈地努力，大地电磁测深法得到了蓬勃发展，因其具有勘探深度大、施工方便、成本低、对低阻体反应灵敏等优点，在地球物理勘探、地质勘查和工程探测等众多领域都发挥着重要作用。大地电磁测深法的最终目的，是得到与实际实际地质情况最为吻合的地电模型。该过程要求对实测资料进行正反演计算，使模型响应与实际资料达到最佳拟合。正演是反演的基础，因此，对复杂地质模型进行高精度快速正演计算是MT数值模拟研究的重点[1-3]。

二维MT的正演问题已相对成熟，如有限差分、积分方程、有限单元等方法均有稳定实现[4-7]。这里着重探讨有限单元法求解大地电磁正演问题。Rodi[8]、Wannamaker等[9]使用规则化矩形网格剖分对大地电磁二维正演模拟进行了研究；徐世浙等[10-11]将原来简单的网格剖分发展为三角单元剖分和三角单元-矩形单元剖分，很大程度提高了大地电磁场场值求解的精度和计算速度。但复杂的地电模型中，传统结构化网格为了保证内节点拓扑结构的一致性，往往需要更多的网格。Kerry Key等[12]、柳建新等[13]利用非结构化自适应有限元网格对二维大地电磁进行研究；Ren等[14]提出了面向目标的自适应矢量有限元法，大大提高了计算精度和适应性；罗天涯等[15]、杨振武等[16]相继利用非结构化网格进行了二维MT正演研究。笔者认为，将非结构化三角网格与h-型自适应算法相结合，一定程度上可提升复杂构造二维正演的模拟精度与计算时间。

笔者主要研究基于非结构化三角网格划分的自适应有限元解决大地电磁的二维正演问题。有限元法首先通过计算将研究域分成许多小单元结构的每个节点电磁场值，接着每个小单元的场值可利用二次插值函数得到，最后可计算出整个研究域的电磁场值。基于非结构化三角形网格剖分的自适应有限元算法，对不规则与复杂结构模型的边界有了更好地模拟，为了提升数值模拟计算精度，采用了基于后处理技术的后验误差估计方法(Dual Error Estimate Weighting, DEW)[12]，对局部网格实现了自动加密。

1 基本理论

1.1 大地电磁的边值问题

考虑电性参数沿走向不变的二维地电模型，则在二维地电结构中，大地电磁场满足偏微分方程：

▽·(τ▽u)+λu=0

(1)

在大地电磁二维正演中，式(1)中电磁波的性质为定态时谐波，记e-iwt为时谐因子。TE模式下，u=Ex,τ=1/iμε,λ=σ-iωε，由于上边界与地面之间距离足够远，取u=1；TM模式下，u=Hx,τ=1/(σ-iωε),λ=iωμ，因空气中的磁场分量不受地下介质电性分布的影响，且为常量，可取地面上的u=1；对于下边界与左右两边界，TE、TM两种极化模式具有相同的边界条件。

1.2 加权余量法

记φ为权重函数，引入加权余量法，式(1)两边同时乘以φ并进行积分，可得式(2)。

(2)

针对式(2)左边的第一项，利用矢量运算式与积分变换式，并将相应边界条件代入可得式(3)。

(3)

将式(3)代入式(2)可得式(4)。

(4)

1.3 二次插值有限元分析

如图1所示，假设O点为三角形的重心，取三角单元内二次插值形函数向量为：

图1 三角单元节点编码及面积坐标Fig.1 Triangular element node coding and area coordinates

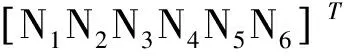
(5)

其中形函数Ni与面积坐标Li的关系为

N1=(2L1-1)L1

N2=(2L2-1)L2

N3=(2L3-1)L3

N4=4L1L2

N5=4L2L3

N6=4L1L3

假设u是三角单元内任意点的电磁场值，则

(6)

将式(6)代入式(4)，消去变分项后得：

(K1-K2+K3)ue=0

(7)

其中，

根据有限单元法的基本法则，进行单元矩阵的扩展，可得总体刚度矩阵：

(8)

代入边界条件后，可得到有限元方程：

Ku=P

(9)

式中：Κ为对称矩阵，是由单元上计算的系数矩阵扩展而来的总体系数矩阵，为了节约计算内存，利用定带宽存储方式，只将矩阵的上三角或下三角元素进行存储，并只对非零元素进行存储。在有限元方程求解过程中，首先采用乘数法对有限元方程添加边界条件，该方法得优势在于对方程的改动较小，程序容易实现，且效率较高[17]；然后利用直接稀疏LU分解法对系数矩阵组成的线性方程组进行求解，得到研究区上的节点场值u，有限元求解完成。

1.4 后验误差估计

在有限元中，当全局网格满足一定的条件后，局部网格的密度对于有限元解的精度有着很大影响，这表明相对于全局网格的细化，更好的细化方案是根据需求有选择性的进行局部区域网格地细化。利用3D-Gmsh进行研究域的粗剖分，将生成的粗网格作为初始网格，然后求解出每个单元节点处的有限元解uh，进而计算出解的梯度值▽uh，得到每个单元内的局部误差为式(10)。

re=‖T▽uh-▽uh‖2(e)=‖(T-I)▽uh‖2(e)

(10)

式中：T为恢复因子；I为单位算子。其中，恢复因子T的超收敛特性对后验误差估计的有效性存在重要影响，故较精确的误差估计表达式为式(11)。

(11)

其中：u为微分方程的真实解；h为每个三角单元外接圆的直径。该方法属于一种全局网格细化的基本误差估计方法，为了实现对局部网格的加密，需要求解一个对偶问题，对原后验误差估计值使用对偶问题的解的后验误差估计值进行加权，即对局部误差re增加一个加权项，多位学者对该问题的定义都已做了详细的论述[14,18]。加权后验误差估计公式为式(12)。

Re=‖k(T-I)▽uh‖2(e)‖(T-I)▽wh‖2(e)

(12)

式中：TE模式时k=1；TM模式时，k=1/σ，wh为对偶问题的解。

1.5 自适应网格剖分

这里采用开源软件Gmsh建立非结构化三角网格，该网格的灵活度较高，可以在场变化剧烈的区域及电性突变界面处的加密网格，对于复杂地电模型有较好的模拟效果。为了更好地符合边界条件，在研究区域以外设定网格稀疏的扩展区域，如图2所示。

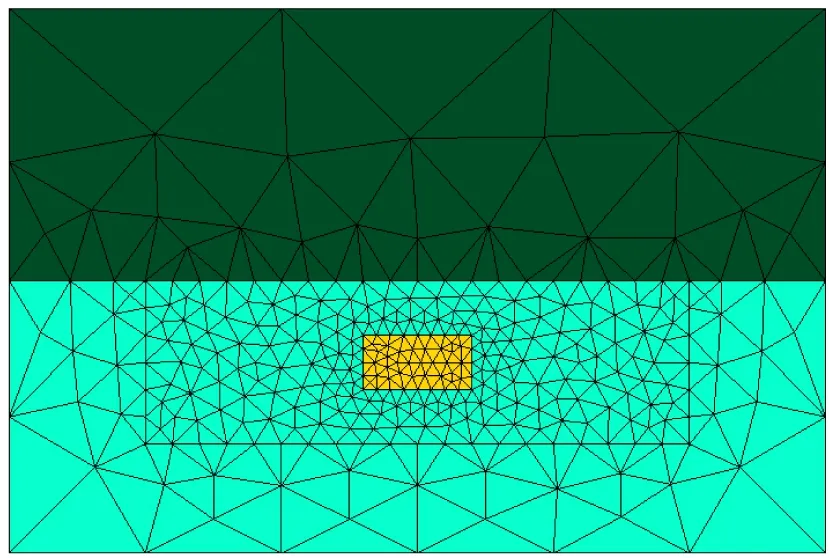
图2 非结构化自适应网格Fig.2 Unstructured adaptive grid

自适应网格细化方式有：h-型、p-型和hp-型三类[19-20]。h-型是通过逐步加密网格，而形函数的阶次保持不变的情况下满足精度要求；p-型是通过改变形函数的阶次，但单元网格的大小维持不变的情况下逼近精确解；hp-型是结合h-型和p-型两种细化方式，虽然细化效果优于前两种方法，但是实现较为困难。笔者采用h-型自适应网格细化技术，利用初始粗网格得到的局部误差为指导进行局部区域的网格细化，对细化后的网格再次进行误差计算，直至细化后的网格误差满足精度要求。

2 算例

2.1 一维层状介质

如图3所示，构建了一个H型水平层状地电模型。其中ρ1=200 Ω·m，h1=2 000 m；ρ2= 100Ω·m，h2= 2 000 m；ρ3=300 Ω·m，层厚无限延伸。测线距离L= 20 km，测点个数N= 101个，点距r= 200 m； 频率f为 10-4Hz～104Hz，取对数(log10)后，以0.2为采样间隔，频点n= 41个，自适应加密后网格数目为8 652。对H型地电模型采用本文算法数值模拟，将模拟结果与解析解、2D矩形网格剖分有限元解成图(图4)分析。由图4可知，视电阻率曲线与解析解视电阻率曲线基本吻合，在高频段，阻抗相位曲线与解析解阻抗相位曲线存在误差。

图3 一维层状介质地电模型Fig.3 One-dimensional layered dielectric geoelectric model

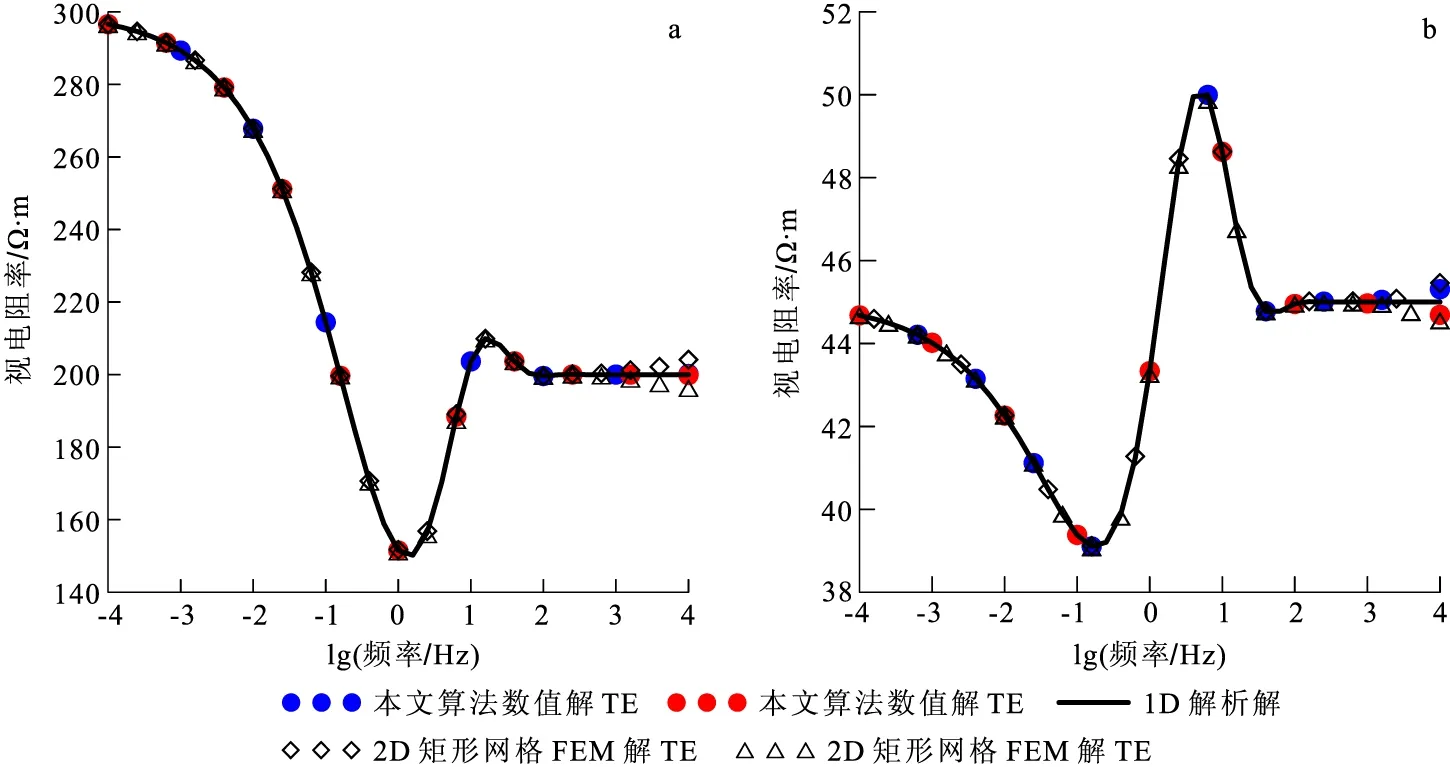
图4 一维层状介质响应曲线Fig.4 Response curve of one-dimensional layered media(a)视电阻率曲线;(b)相位曲线

表1 误差统计表

使用电阻率相对误差百分比和相位误差绝对值来评估精度，其计算公式如下：

(13)

(14)

式中：ρs为解析解视电阻率值；ρa为有限元解的视电阻率值；φs为解析解阻抗相位；φa为有限元解的阻抗相位；n为频点个数。分别选择矩形网格与非结构化三角网格进行数值模拟，计算两种模式下有限元解与数值解的误差(表1)。

在网格节点数量大致相同的情况下，通过表1可知，2D非结构化三角网格FEM数值解的视电阻率的误差比矩形网格小，且在计算速度上得到了一定的提升。

2.2 COMMEMI-2D1模型

对COMMEMI-2D1模型(图5)进行数值模拟，旨在验证该算法对二维构造的有效性。如图5所示，在电阻率ρ2=100 Ω·m的地下均匀半空间存在一个电阻率ρ1= 0.5 Ω·m的低阻异常体，其宽为1 km，高为2 km，顶面距离地表0.25 km；设置长度L=40 km的测线，测点数N=81，测点间距r=0.5 km。为了与Zhdanov等[21]发布的结果进行对比验证，使用本文算法选取10 Hz频率进行数值模拟(图6)。

图5 COMMEMI-2D1模型Fig.5 COMMEMI-2D1 model

由图6可知，本文算法在TE和TM两种模式的模拟结果与Zhdanov等[21]提供的数据基本吻合，说明了计算方法的正确性。根据响应曲线可知，在低阻异常体的边界处，TE模式视电阻率产生明显的突跳增大，而TM模式相对变化平缓，且TE模式视电阻率受低阻体的影响范围较TM模式更广，曲线体现出向上的开口更大。

图6 COMMEMI-2D1模型Fig.6 COMMEMI-2D1 model(a) TE模式;(b) TM模式

2.3 起伏地电模型

2.3.1 地垒模型

如图7所示，构建一个地垒模型。模型上方电阻率ρAi r= 108Ω·m，下方电阻率ρ= 100 Ω·m，起伏地表水平范围为-800 m～800 m，高度为500 m，凸起部分范围为-200 m～200 m，研究区范围为-3 000 m～3 000 m，在地表设置86个测点。采用非结构化三角形单元进行网格粗剖分，经过10次细化迭代，自适应加密之后的网格单元数为7 640，网格节点为3 467(图8)。利用自适应有限元法对该模型进行正演计算，选取0.01 Hz、1 Hz、100 Hz 3个频点，可得两个模式下的正演响应曲线(图9)。

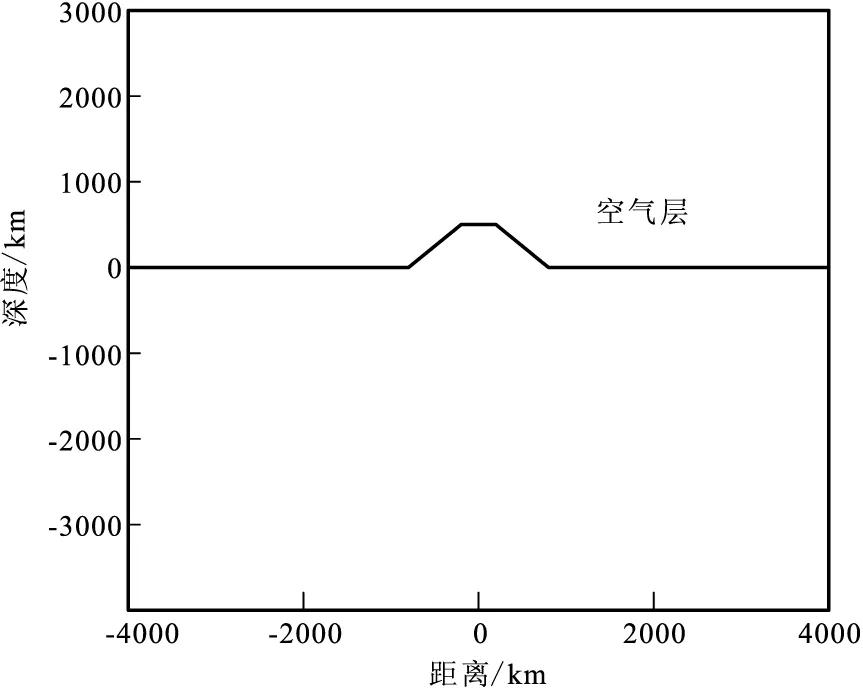
图7 地垒模型示意图Fig.7 Schematic diagram of the land barrier model

图8 地垒模型自适应网格Fig.8 Adaptive grid for basement model

地垒模型对图9(a)、图9(b)、图9(c)与图9(d)中的曲线都产生了不同程度的影响。其中，对于视电阻率曲线而言，两种模式下的曲线是反向的， TE模式下曲线随频率的波动范围要明显低于TM模式，且图9(c)曲线在地形变化处(-800 m、800 m、-200 m和200 m)的突变程度明显高于图9(a)曲线； 而对于相位曲线而言，地垒模型对二者的影响很接近，其与频率的变化大致成正相关，且在地形变化处(-800 m、800 m、-200 m和200 m)曲线的突跳大致相同。

2.3.2 地堑模型

如图10所示，构建一个地堑模型。模型参数与地垒模型参数相同，采用非结构化三角形单元进行网格粗剖分，经过12细化迭代，自适应加密之后的网格单元数为9 860，网格节点为4 617(图11)。采用自适应有限元法对该模型进行正演计算，选取0.01 Hz、1 Hz、100 Hz 3个频点，可得两个模式下的正演响应曲线(图12)。

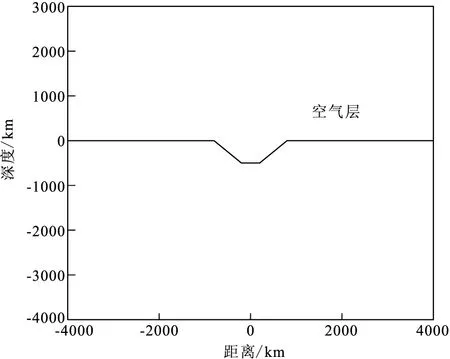
图10 地堑模型示意图Fig.10 Schematic diagram of the mantle model

图11 地堑模型自适应网格Fig.11 Adaptive grid of graben model

由图12可知，地嵌模型对两种极化模式下的视电阻率曲线和阻抗相位曲线都产生了一定程度的影响。对于视电阻率曲线，两种极化模式下的曲线是反向的， TE模式下曲线受地形起伏影响比TM模式更加明显，且图12(c)曲线在地形变化处(-800 m、800 m、-200 m和200 m)的突变程度明显高于图12(a)曲线； 而对于相位曲线，地堑模型对二者的影响很接近，其与频率的变化大致成正相关，且在地形变化处(-800 m、800 m、-200 m和200 m)随着频率的增大曲线突跳明显。

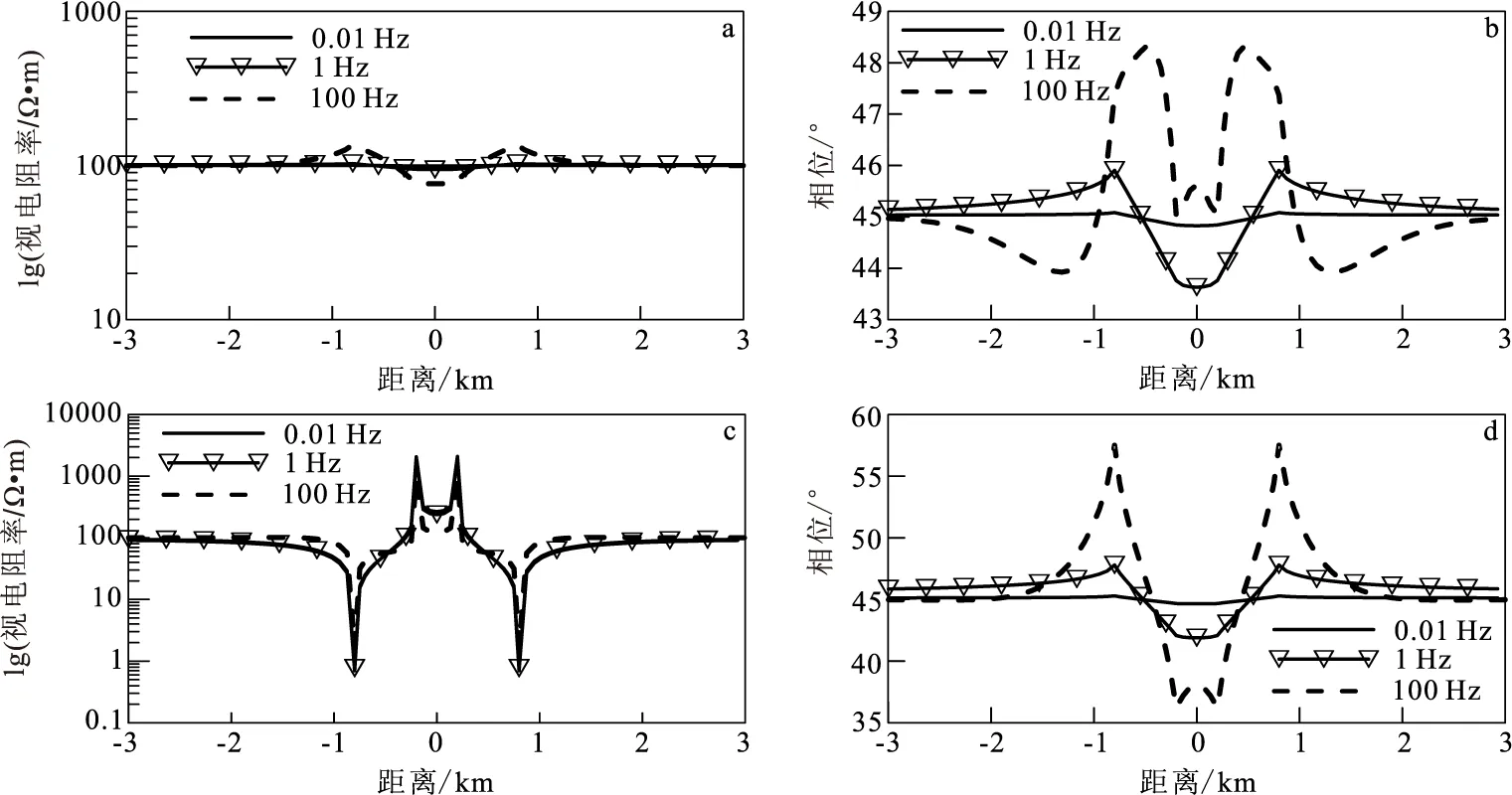
图12 地堑模型自适应有限元二维正演响应曲线Fig.12 Adaptive finite element 2D forward response curve of graben model(a)TE模式视电阻率曲线;(b)TE模式阻抗相位曲线;(c)TM模式视电阻率曲线;(d)TM模式阻抗相位曲线

2.4 复杂构造模型

2.4.1 组合异常体模型

构建如图13所示的地电模型。在电阻率为100 Ω·m的均匀半空间，存在电阻率为10 Ω·m的低阻块体和电阻率为1 000 Ω·m的高阻块体。两块体大小相同，距离地面埋深均为1 000 m，两块体之间相距4 000 m。

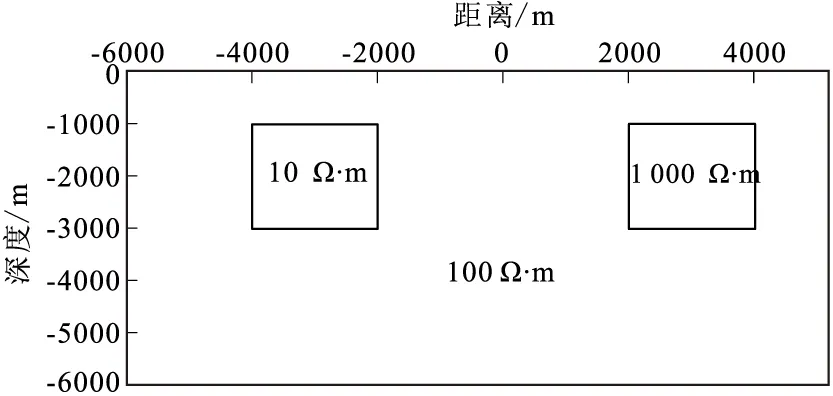
图13 组合异常体模型示意图Fig.13 Schematic diagram of combined abnormal body model

采用非结构化三角形单元进行网格粗剖分，经过3次细化迭代，自适应加密之后的网格单元数为6 100，网格节点为2 788(图14)。采用自适应有限元法对该模型进行正演计算，得到二维正演响应剖由图15可知，两种极化模式下的正演结果都很好地刻画了两个异常体的基本特征，TM极化模式对异常体的正演响应显得更加灵敏，而TE极化模式对异常体的分辨率稍差。再者，正演响应结果对低阻异常体的分辨率比较高，而对高阻异常体的分辨率较差。

图14 组合异常体模型自适应网格Fig.14 Combined anomaly model adaptive grid

图15 组合异常体模型自适应有限元二维正演响应剖面图Fig.15 Adaptive finite element two-dimensional forward response profile of combined abnormal body model(a)TE模式视电阻率图(b)TE模式阻抗相位图;(c)TM模式视电阻率图;(d)TM模式阻抗相位图

2.4.2 断层模型

构建如图16所示逆断层模型，断层上下盘均为层状均匀介质，地电结构为KH型，电性参数如图16所示。断层倾角为45°，断层上下盘断距为500 m。采用非结构化三角形单元进行网格粗剖分，经过3次细化迭代，自适应加密之后的网格单元数为3 497，网格节点为1 430(图17)。

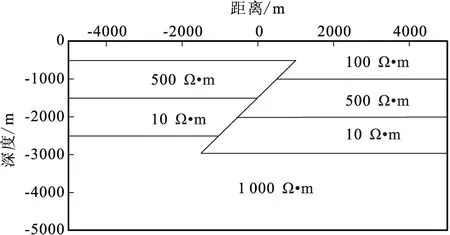
图16 断层模型示意图Fig.16 Schematic diagram of fault model

图17 断层模型自适应网格Fig.17 Fault model adaptive grid

图18是TE、TM两种极化模式下断层模型的二维正演响应剖面图。从图18(a)、图18(c)可得出，对断层上盘的K型地电模型的三层地层有较为清楚地分辨。高频部分断层破碎带处出现等值线错断。上盘的表层厚度反应明显比下盘厚度薄，反应上盘地层有相对下盘地层而言有抬升；低频时， TM极化模式下的视电阻率图中等值线出现错动。从图18(b)、图18(d)可得出，高频时，对浅表及中部地层的抬升分辨较高，底界面埋深差别明显分辨，左高右低；低频时，TE极化模式下的等值线变化不明显，TM极化模式下的等值线在断裂处出现扭动。

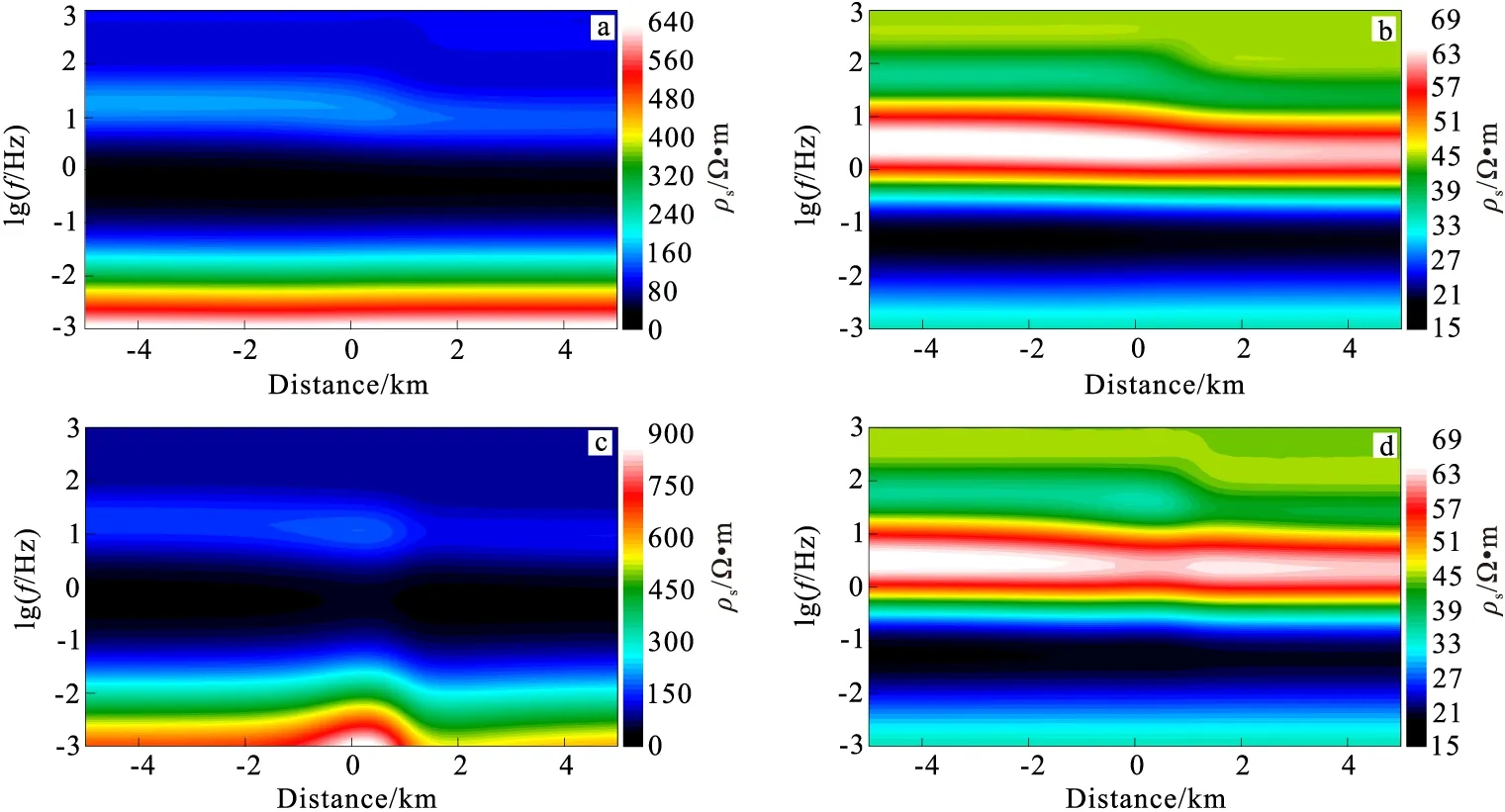
图18 断层模型自适应有限元二维正演响应剖面图Fig.18 Fault model adaptive finite element 2D forward response profile(a) TE模式视电阻率图;(b)TE模式阻抗相位图;(c)TM模式视电阻率图;(d)TM模式阻抗相位图

3 结论

通过Gmsh剖分的非结构化三角网格作为初始网格，应用对偶误差估计加权法对初始网格进行自适应细化，构建了一维层状模型、COMMEMI-2D1模型与起伏地电模型，通过解析解、2D 非结构化三角网格FEM解与2D矩形网格FEM数值解的试算对比分析，得到以下结论：

1)通过一维层状模型，验证了本算法的准确性。

2) 通过与2D矩形网格FEM数值解地对比，验证了本文算法有较高精度。

3)通过复杂模型与起伏地电模型，计算并分析了两种模型的二维MT响应特征，可作为实测MT数据质量评价、静态效应研究的参考资料，进一步表明本文算法存在使用价值。

4)自适应网格加密相对全局网格加密能够节省计算量，非结构化网格相比矩形网格能够更好地适应起伏地形和复杂异常体。