地震初至拾取奇异值编辑在快速处理中的应用

钟家均, 凌 航, 曾 涛

(中石化西南油气分公司 勘探开发研究院，成都 610041)

0 引言

初至拾取一直是地震勘探中的一个基础而又非常重要的问题。初至拾取是地表低速带静校正的基础，特别是在近地表结构较为复杂的地区，准确拾取地震波走时还是地震层析成像方法中计算速度的重要依据[1]。迄今为止，许多专家学者以及专业领域的开发者都针对初至拾取开展了大量的工作，目前绝大多数处理系统(Omega、Geovation等)或者静校正软件(ToModel等)均有初至自动拾取的功能，笔者也查阅了大量的文献，但几乎都是讨论如何准确求取初至位置的方法和原理，对于自动拾取初至后产生的大量不正确初至值(初至奇异值)如何处理，很少有文献提及。王振国[2]研究提高记录信噪比提高初至拾取的准确性；左国平等[4]介绍使用改进的能量比实现一种简洁易于实现的初至自动拾取方式；陈仲平等[8]讨论利用空变时窗约束条件增加初至自动拾取位置的准确性；徐钰[10]则着重讨论利用时窗、相位、能量等多种因素实现自动准确高效拾取初至，也简单提及了如何删除部分初至奇异值点的方法等。基于此，笔者重点讨论如何在获得了自动拾取初至数据集的基础上，利用文中介绍的方法原理，编程实现初至奇异值的自动编辑剔除，大幅度减少人工进行初至修改的操作，最终保留真实准确的自动拾取的初至数据，达到快速获取准确静校正量的目的。

1 奇异值编辑的实践基础

1.1 初至数据的表现特征

理论模型正演数据表明，无论是水平地表还是起伏地表，初至在空间都表现出一定的连续性(图1)，如初至与炮检距、道顺序和炮桩号等存在多因素的变化关系[6](图2～图5)。初至数据包含一些严重不满足这种关系的独立或者有一定连续性的大值起跳点，即初至奇异值点。

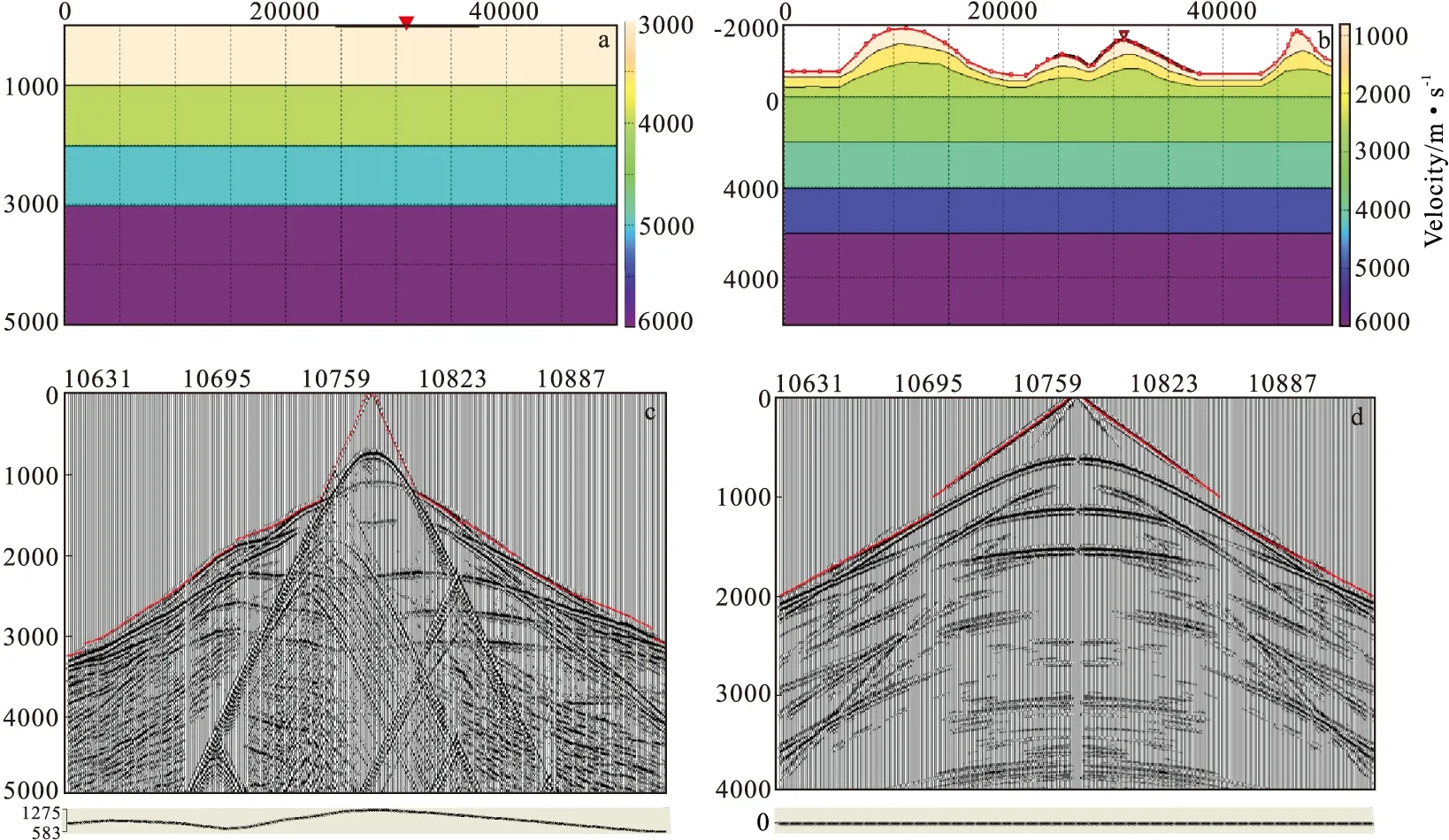
图1 层状介质理论地质模型及其模拟记录Fig.1 Theoretical model of layered media and corresponding simulation records(a)水平地表模型;(b)起伏地表模型;(c)水平地表模拟记录;(d)起伏地表模拟记录

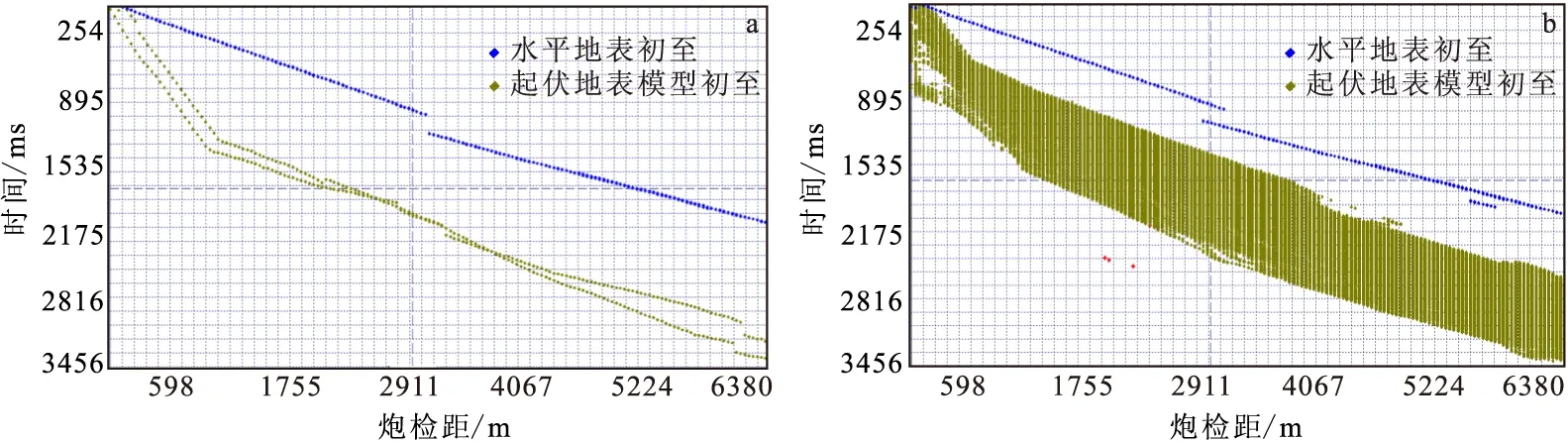
图2 两种模型的初至叠加显示Fig.2 First break superposition of the two models(a)单个炮记录初至叠加显示;(b)所有炮记录初至数据叠加显示

1.2 剔除部分冗余初至对层析静校正量的影响

一般情况下，处理人员希望一炮不漏的获得逐道准确的初至信息。但复杂的地震地质条件使得炮点初至变化复杂，各种干扰导致地震道初至前背景不干净，岩性差异导致激发能量传递不一致而影响初至起跳的强弱，手工拾取初至会受到较大的人为因素影响，看漏、看错不可避免等。因此，尽量减少人为因素干扰，利用自动拾取初至和并快速去除那些初至值不正确的点是目前最为快捷的一种方式。但剔除这些不正确的点，势必导致初至数据量减少，在目前覆盖次数较高的地震采集技术方法下，当出现初至漏失会产生影响，我们以某工区手工拾取初至数据为基础，对不同的初至数据集产生的静校正量进行了分析。在随机减少10%～50%的有效初至进行初至层析反演，采用统一的反演参数，获得其速度模型和静校正量。图6是原始初至数目和在此基础上减少40%的静校正量对比，表1是针对不同的模型参数和不同的初至数量进行层析反演之后的实际效果对比分析。由图6与表1分析及层析反演静校正量实际计算可知，对于高覆盖次数的地震数据道，去掉部分冗余初至对层析静校正量影响不大。特别是基于近地表速度模型的基准面静校正量，控制形态和构造成像的长波长静校正量，五种方式不存在明显的差异。因此，我们有理由认为，在初至数据存在冗余的情况下删除部分初至数据对静校正量影响很小。

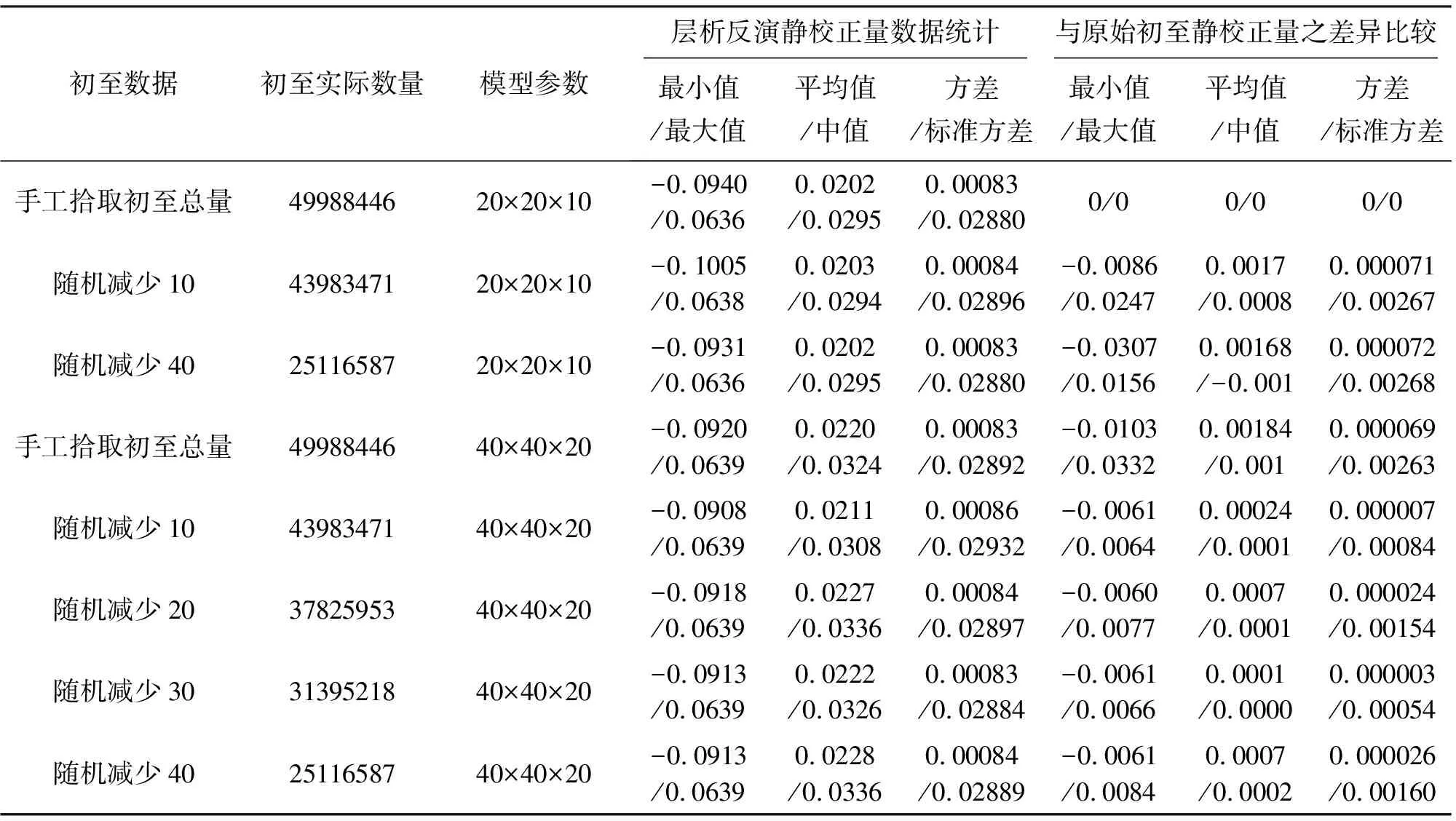
表1 手工拾取初至总量和在其基础上随机减少不同比例的静校正量对比表

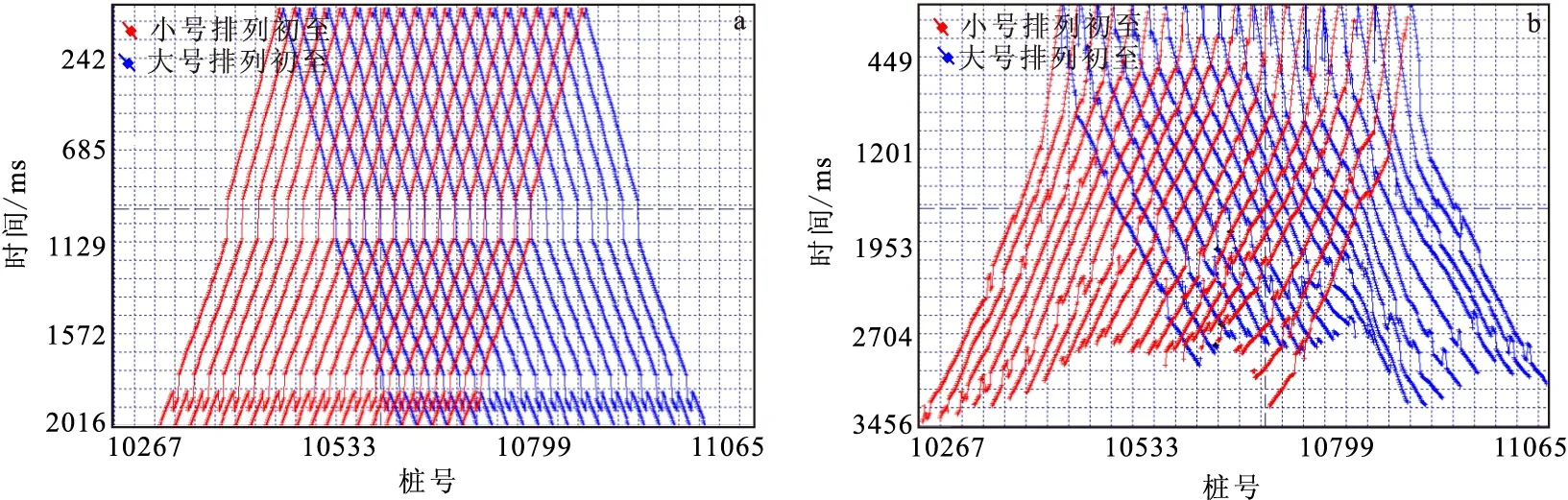
图3 共炮点初至数据表现为一定连续性的曲线形态Fig.3 The first break data of common shot points show a certain continuous curve shape(a)水平地表;(b)起伏地表

图4 共检波点初至数据表现为一定连续性的曲线形态Fig.4 The first break data of co-detection points show a continuous curve shape(a)水平地表;(b)起伏地表

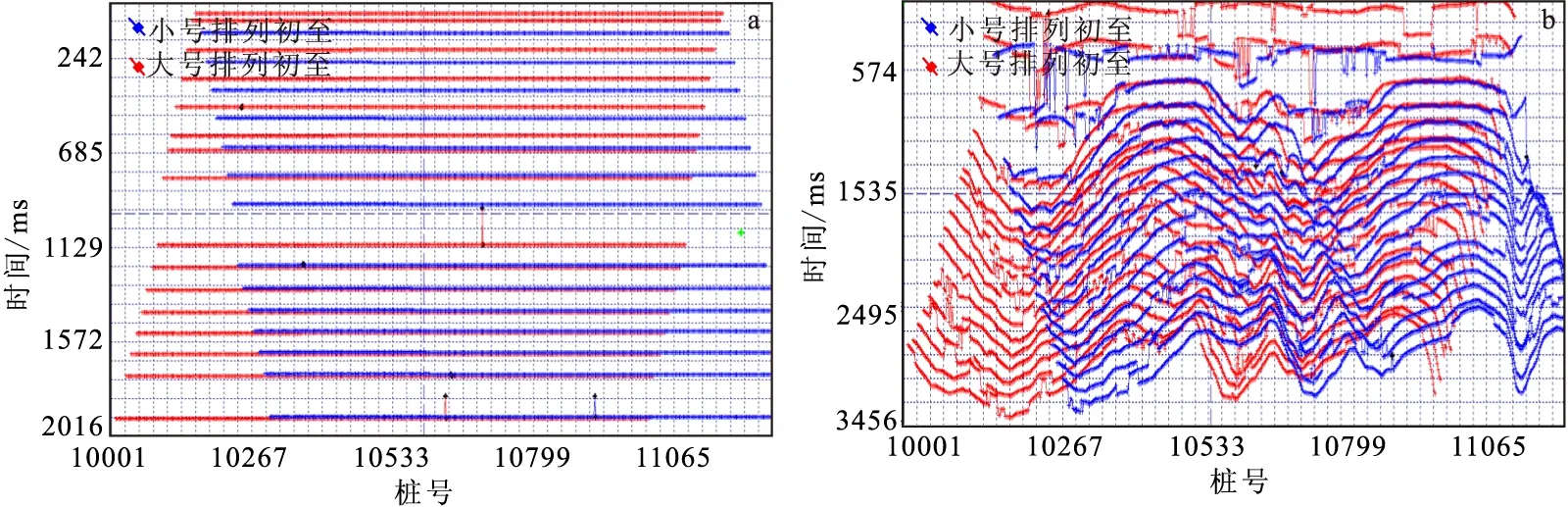
图5 共炮检距初至数据表现为一定连续性的曲线形态Fig.5 The first arrival data of common offset show a certain continuous curve shape(a)水平地表;(b)起伏地表

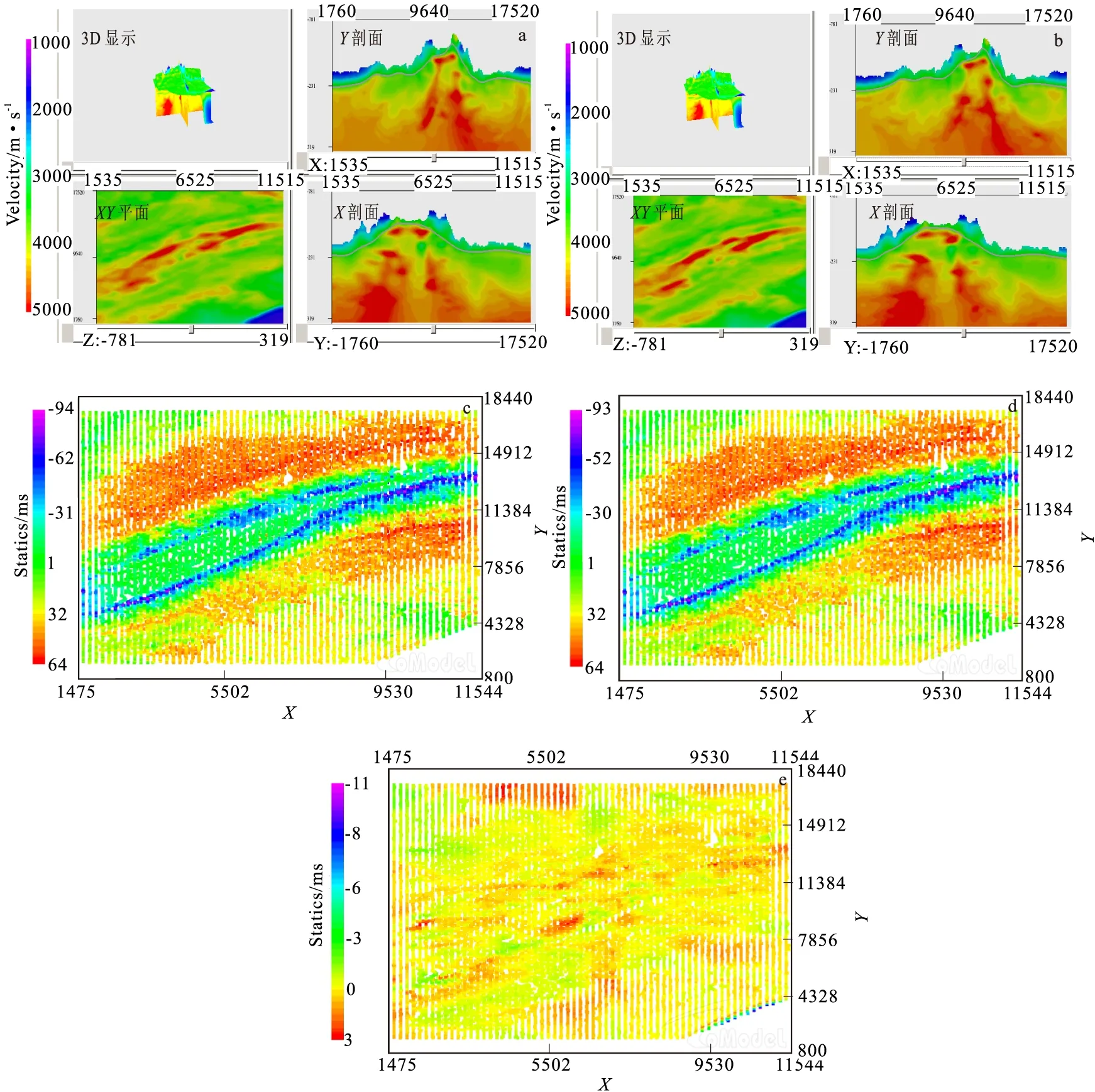
图6 手工拾取初至总量和在其基础上随机减少40%的层析反演模型和静校正量对比Fig.6 Comparison of tomographic inversion models and static corrections based on first break collection of manual picking up and random 40 % reduction(a)原始初至数据反演的近地表速度模型;(b)减少40%初至后反演的近地表速度模型(c)原始数据静校正量;(d)减少40%初至的静校正量;(e)原始初至和减少40%初至静校正量之差

1.3 快速准确拾取初至是资料快速处理的重要保证

随着勘探开发进程加快，资料处理项目的时间节点安排变得越来越紧凑，资料快速处理任务也越来越多，工作量大、时间紧。而利用初至数据的层析静校正，是常规处理中较为准确而又相对稳定的静校正量获取方法[3，9]。在短期内能够获得较为准确的静校正量，一直是资料处理人员需要达成的目标。因此，想尽一切办法获得接近真实的初至拾取数据，拾取速度就决定了静校正量的获取速度，也决定了能够获得更加准确的初至折射或者层析静校正量。

2 初至奇异值剔除编辑思路

目前地震数据利用初至拾取软件进行自动拾取的效率高，而且可供选择的拾取方法也很多。笔者讨论利用自动拾取初至的结果，并根据初至奇异值的分布规律和特征，讨论提出剔除初至奇异值需要完成的数据准备和基本操作方法，并设计提出初至的数学模型，然后根据此模型估算剔除初至奇异值，从而完成初至奇异值从正常初至数据集中分离剔除操作。

2.1 自动拾取初至的结果的获得

在进行本方法编辑初至之前，需要采用适合该工区自动拾取精度比较高的初至拾取方法(可以自己编程实现，也可以利用处理系统或者静校正软件等完成)对地震数据批量自动拾取一遍初至(图7)，将初至数据保存到地震数据到头或者单独的指定格式文件中。需要注意的是，无论采用什么样的自动拾取方法，应保证全区初至拾取位置的一致性。

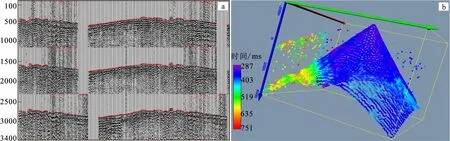
图7 部分排列自动拾取初至(已线性动校)和某炮初至数据在空间上的展布Fig.7 First break ( linear motion correction ) of partial spread of a shot and spatial distribution of first break of a shot(a)自动拾取的部分排列初至点(红色点);(b)单个炮点初至空间分布(含奇异值点)

2.2 初至奇异值的分布规律

自动拾取之后的初至包含着许多的奇异值点(图8)，如果保留，会严重影响初至拾取的质量，如果直接应用于初至层析静校正的反演中，会大大降低静校正量获取的质量。手工操作拾取初至时，主要是逐个排列去查看并执行删除或者重新拾取操作，这种工作量很大，费时又费力。通过观察和实际拾取操作，发现需要手工拾取和修改初至的部分符合以下几个规律：

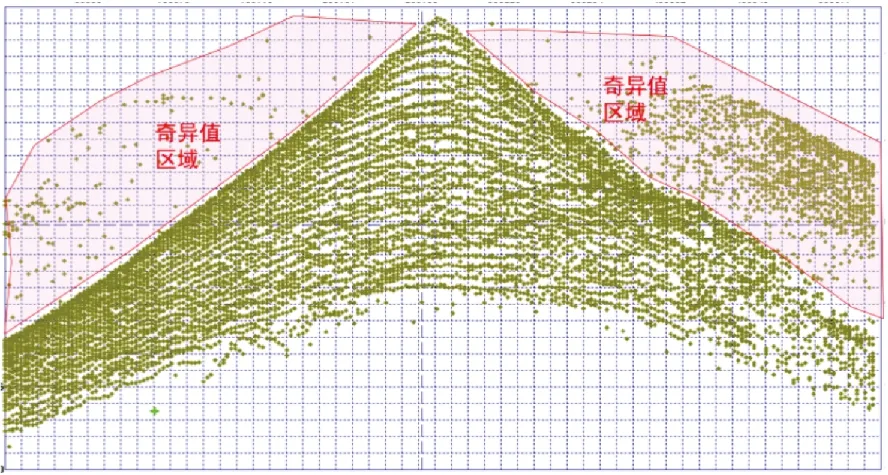
图8 某三维炮点自动拾取初至及伴随的奇异值Fig.8 The first break and the associated singular values of all the three-dimensional shot points by automatically picked up

1)初至值随炮点、检波点位置和炮检距的变化步调突然不一致。

2)拾取位置常出现在地震道信噪比低或者地震道初至前干扰特别严重的位置。

3)删除奇异值初至的操作较为多且频繁，相对简单容易，但拾取初至的几率较少，且操作显得更为复杂。

4)总是希望找到一次性的去掉异常值的方法，然后集中精力进行拾取检查操作。

5)希望能够看到和处理的初至更集中、更多等。

据上述初至拾取工作特点，希望找到一种软件实现奇异值的自动剔除，借助可视化界面将初至数据进行集中分析处理，进行少量的操作之后视情况开展下一步精细拾取工作，减少因为肉眼观察失误或者视觉疲劳而漏拾的现象，这样会大大缩短初至拾取的时间，提高初至拾取质量和效率。

2.3 奇异误差值的估算与控制模型

前人研究表明[5-7]，无论是理论模型还是实际初至数据，影响初至值大小的几个关键因素主要为激发点和检波点的空间位置关系。从理论模型的初至数据来看，无论地表如何起伏弯曲，其初至的连线形态是基本连续的，初至的变化值应该是在一定的限制值范围之内，如果突破了这个限制值的范围，就会出现极不协调的孤立拐点(奇异值点)。处理奇异值点有很多种方式，比如初至数据统计、曲线拟合逼近等(图9)，这里运用最易实现的相邻初至差分散程度统计计算方法。

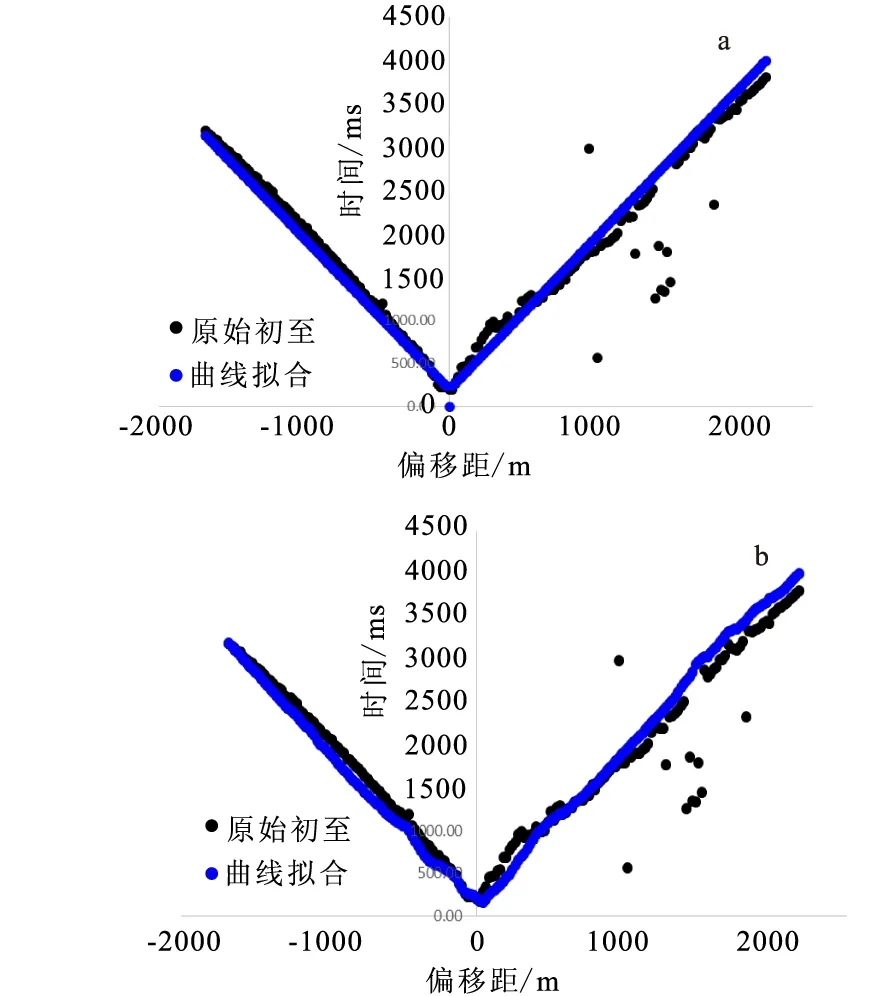
图9 一种合适的拟合初至的方法Fig.9 A suitable fitting curve of first break(a)实际初至与线性拟合对比;(b)实际初至与加上修正量之后拟合对比

在相同的数据集中，相邻两个初至数据点的差值制约条件是基本固定的，这种差值不会无限制的增加或者减少，可以利用统计规律进行初至奇异值排除。统计规律排除的基本原理如下：

1)手绘初至数据集中趋势线，如果每个初至点的坐标为yi(xi,ti)，集中分布趋势线可以假设首尾点的坐标分别为y1(x1,t1)和y2(x2,t2)可以使用两点式的直线方程表示：

(y-t1)/(t2-t1)=(x-x1)/(x2-x1)

式中要求x1≠x2，t1≠t2。可以利用点到直线的距离公式求出每个初至点距离趋势线的距离。然后根据指定的距离阈值判断每个初至，根据设定的阈值进行计算排除(图10)。

图10 利用手绘集中区域初步排除奇异初至值Fig.10 Preliminary exclusion of singular initial values by using hand-painted concentrated regions(a)手工绘制集中区域趋势线;(b)旋转至水平方向并标记奇异值的初至数据

2)将一个有序的初至数据集合，看作一个与桩号、炮检距或者高程等有密切联系的一些列离散函数值。利用相邻初至差的分散程度实现初至数据的再次过滤，这种分散程度使用最常规的统计计算方法就可以实现。设一个标准道距为dx(dx>0)，

ti代表第di(i=1,2,3……,n)数据道初至时间值，则相邻一个标准道距的两个数据道之间的数值差Δt可以表示为：

Δti=ti+1-ti(i=1,2,3，…,n-1)

(1)

野外排列位置变化很复杂，炮点及接收点道的分布总是不均匀的。考虑到初至值的变化与接收点的空间位置密切相关，在进行奇异值误差估计时需要尽量考虑排列长度、高程值等关键因素的影响。笔者先不考虑低降速带的变化，仅从地形考虑，如果空间位置增大，相邻两道之间的初至之差也会增大，如果接收道位置增高，相邻两道之间的初至之差也会增加。我们需要根据实际初至统计与排列长度和高程值相关的一个修正量ki，最简单的就是排列长度增量kx和高程变化增量kz，用于增大初至差的容错率。这种初至差转化为标准道距的修正值可以表示为：

(2)

修正之后的初至差序列为Δtki=kiΔti，然后利用常规的统计学求取Δtki数值序列的平均值Δtka、标准方差Δtks。

对于修正之后的每一个初至差值，其与均值的偏离程度可以用式(3)表示。

dki=|Δtki-Δtka|

(3)

如果一个数值序列确定，那么Δtka和Δtks将都是定值。我们可以利用Δtka和Δtks设置奇异值过滤阈值。这个阈值定义为：

Bi=[(dki-CΔtks)>0]

(4)

其中：Bi为奇异值排除阈值；C为给定校正常数。以求取的dki大于CΔtks为奇异值判断标准，如果超过视该初至值为奇异点，对相应初至置删除标记。针对具体工区，C值可以先利用几炮数据手工拾取之后由程序统计确定。奇异值筛选应保证所在数据集具有一致性，如常用的数据集有共炮点数据集、共接收点数据集和共炮检距数据集(图11～图12)。

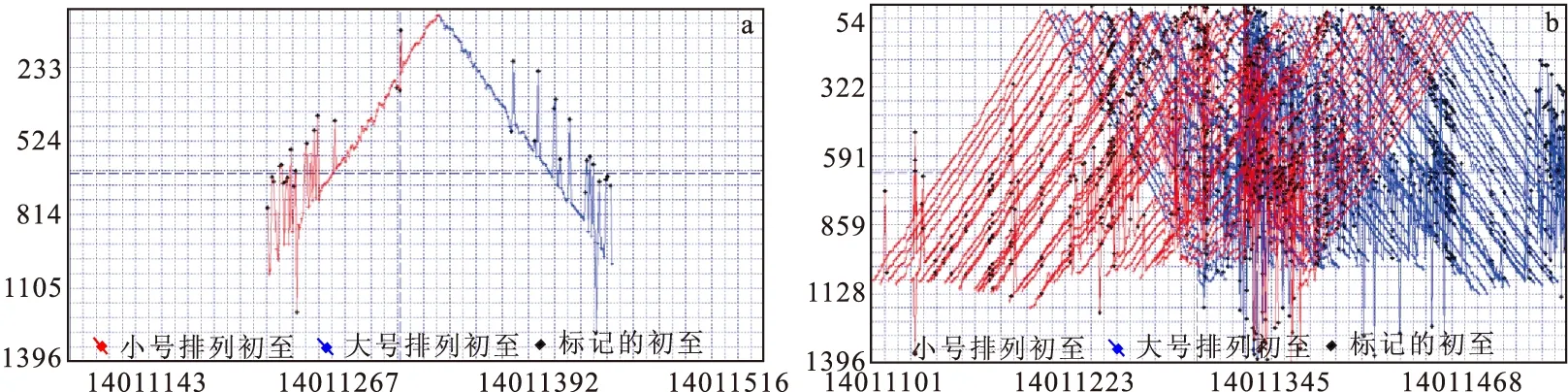
图11 共炮点道集上进行排除(黑点标记)Fig.11 Marking of common shot gathers(black markers)(a)一个排列初至数据;(b)多个排列的初至数据奇异值筛选

图12 共接收点和共炮检距数据筛选(黑点标记)Fig.12 Result of screening of common receiver points and common offset points datasets(black markers)(a)共接收点初至数据筛选结果;(b)共炮检距数据集筛选结果

3 应用实例及效果

在某三维工区中进行了六千余炮的初至拾取排除测试，实际人工拾取需要4个人努力花费15 d左右才手工拾取完成。但从拷贝数据开始至最终完成阈值筛选，利用此自动剔除方法仅花费1 d的时间。首先在共炮点道集上初至数据进行判断和排除标记(图13～图14)；其次利用前面的筛选结果又切换至共接收点初至数据集和共炮检距初至数据集中进行类似的计算排除；再次根据前面筛选排除结果迭代进行，最终消除了绝大部分奇异值，最大程度的保留有效初至，留下极为少数的奇异值初至数据点(图15)，最终获得的初至总数为4 490×104个，介于手工拾取初至总量和在手工拾取初至总量基础上随机减少10%的数目之间。

图13 某炮点排除奇异值点之后效果Fig.13 The effect after excluding singular value points of a shot point(a)利用阈值筛选初至显示;(b)部分排列放大显示

图14 某炮点部分排列初至数据奇异值排除前后在地震道集上的对比Fig.14 Comparison of seismic traces before and after elimination of singular values of first break data from partial spread of shot points(a)某排列自动拾取初至结果;(b)奇异值阈值排除之后的结果

图15 初至阈值筛选前后叠加对比Fig.15 Overlay comparison of first break before and after threshold screening(a)单个炮点奇异值筛选前后对比;(b)全部炮点奇异值筛选前后对比

图15是自动拾取结果和阈值筛选奇异值之后的初至数据叠加显示，从图15中可以看出，自动拾取后的初至中(草绿色)包含有大量的奇异值点；经过阈值方式编辑处理之后的初至(蓝色)奇异值点几乎去得很干净，其中也可能包含去掉的部分有效初至数据。图16是手工拾取初至和阈值筛选初至后获得的层析静校正叠加剖面。通过比较可以看出，两种剖面在构造形态几乎没有差别，静校正量差异是很微弱的。

图16 手工拾取初至与和阈值筛选初至层析静校正量叠加剖面对比Fig.16 Comparison of tomographic static correction stack section between of manual picking and threshold screening first break(a)手工拾取初至后层析静校正叠加剖面;(b)阈值筛选初至后层析静校正叠加剖面

最后一步是进度最慢的一步，可以根据需要安排人手开展工作。将筛选之后的初至数据与地震数据进行关联，进行人工检查或者后续的人工拾取操作，删除做好标记的所有初至，输出最终拾取结果。当然，也可以视情况直接使用编辑之后初至数据获取快速处理项目的静校正量，用于后续的精细初至拾取和精细处理项目之中。

4 结束语

在进行初至奇异值自动编辑剔除的过程中，有如下几点认识：

1)利用软件进行初至奇异值处理，能够节约大量的人力劳动，也不容易出现初至奇异值剔除失误，实现最大程度地改善因奇异值点的影响带来的静校正量误差，明显提高工作效率。

2)本方法只是一个抛砖引玉的方法，不是初至编辑的万能法。这种方法对于初至的变化趋势与地形和低降速层变化呈线性关系较强的地区适应性较好。因为筛选初至需要一定的误差控制，所以筛选过程中会出现某些奇异值不能排除，或者将一些有效的初至数据给排除掉。需要在实际应用中与实际地震数据对比，反复修改，让筛选参数更适合实际需要。

3)使用本方法可以减少初至拾取工作量，但无论何种软件对初至自动拾取不可能达到百分之百准确，还是需要部分人工干预。但在对工程项目要求时间紧工作量大的情况下，此法能够提供较为准确的快速处理静校正量，并为下一步人工精细拾取做好准备。

4)在保证自动拾取初至效果准确率很高的情况下，选定的排除拟合函数不同，初至最终排除效果也会不一致。使用逼近真实初至的拟合函数和抓住关键影响因素，排除绝大多数初至奇异值，获得准确的初至数据和高精度的静校正量才是最终目的。