流体饱和正交裂缝孔隙型介质数值模拟及波场特征分析

王钰鹏, 李小斌, 阎建国

(成都理工大学 地球物理学院,成都 610059)

0 引言

裂缝是油气重要的运移通道和储存空间，因此裂缝发育的地层是良好的油气储集层。对裂缝介质各向异性的研究，主要是通过等效介质理论建立裂缝参数与地震各向异性之间的联系。相对发展成熟的传统等效介质理论有Hudson扰动理论[1]、Thomsen 等径孔隙理论[2]、线性滑动理论[3]和Chapman多尺度裂缝等效介质[4]。

近年来，许多学者充分考虑介质的裂缝、孔隙以及之间的流体交换作用，提出了一系列的等效介质模型。Parra[5]结合BISQ喷流机制和Thomsen模型；分析在不同方位角和入射角传播的地震波的速度频散和衰减特性;Gurevich[6]将线性滑动理论和Gassmann各向异性理论相结合，推导了垂直裂隙和孔隙液压连通的等效模型；杜启振等[7]利用线性滑动理论、Biot孔隙介质理论和连续介质渗流模型建立了裂缝诱导各向异性双孔隙等效模型，推导了速度应力方程，并使用有限差分方法进行了数值模拟；Bakulin等[8]依据线性滑动理论，给出了正交介质的弹性系数计算方法；张显文等[9]利用BISQ机制推导了双相正交各向异性介质的频散方程，研究了地震波的衰减频散方位特性；高炜等[10]将Biot双相介质理论和Gurevich模型相结合，推导了裂缝诱导双相介质模型的弹性波传播方程；刘财等[11]使用伪谱法对高炜建立的模型进行数值模拟，研究其波场特征；张繁昌等[12]将裂缝看作高孔隙薄层周期层状模型，结合Biot方程，推导了裂隙介质的刚度系数与频率的关系，分析孔隙和裂缝之间的不同类型的挤喷流影响。

为了研究正交裂缝，孔隙并存时，裂缝参数对波场传播特征的影响，笔者参照了Gurevich的思路，首先利用线性滑动理论，建立两组相互正交的裂缝，然后通过各向异性Gassmann方程，引入孔隙背景，最后使用Biot双相介质理论弹性波传播方程，用有限差分方法进行数值模拟。通过分析波场特征，进一步认识裂缝性储层的地震波传播规律。笔者所建立的这种模型旨在模拟和分析“裂缝、孔隙、流体共存”介质中的波场特征，为地震储层预测及方法研究提供一些参考。

1 基本原理

1.1 孔隙介质

本次研究所建立的模型如图1所示，含两组相互正交的裂隙，一组裂隙法向平行与x轴的竖直裂隙，另一组法向平行与z轴的水平裂隙。在实际储层中，竖直裂隙常常由构造运动造成，水平裂隙提供了流体流动和储集空间。模型的背景岩石为各向同性高孔隙性介质。

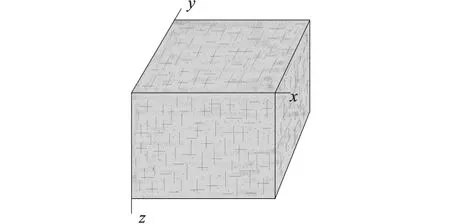
图1 正交裂隙孔隙型介质Fig.1 Orthogonal fractured porous medium

在各向同性介质中，引入均匀分布的孔隙，结果为含孔隙的各向同性介质。使用以下经验公式来计算引入孔隙后的弹性模量[13]，

K=(1-α0)Kg

(1)

μ=(1-α0)μg

(2)

(3)

式中：k、μ分别为含孔隙岩石体积模量和剪切模量;kg、μg分别为背景岩石颗粒的体积模量和剪切模量;φp孔隙的孔隙度。

1.2 正交裂缝

按照Schoenberg理论，整个介质的弹性柔度张量表示为式(4)。

(4)

(5)

另一组旋转不变性裂隙法向平行于z轴时，设n3=(0，0，1)，则柔度张量可以写成式(6)形式。

(6)

因此，当介质中同时含有一组法向平行于x轴和一组法向平行于z轴的裂缝时，介质的柔度张量可以表示为式(7)。

S0=Sb+Sf1+Sf2

(7)

对式(7)求逆可得正交裂缝介质的弹性系数。

C11=(λ+2μ+4μ(λ+μ)ZN2)/[(λ+2μ)·

(ZN1+ZN2)+4μ(λ+μ)ZN1ZN2+1]

C12=(λ+2λμZN2)/[(λ+2μ)(ZN1+ZN2)+

4μ(λ+μ)ZN1ZN2+1]

C13=λ/[(λ+2μ)(ZN1+ZN2)+

4μ(λ+μ)ZN1ZN2+1]

C22=[λ+2μ+4μ(λ+μ)(ZN1+ZN2)+

(8μ3+12λμ2)ZN1ZN2]/[(λ+2μ)·

(ZN1+ZN2)+4μ(λ+μ)ZN1ZN2+1]

C23=(λ+2λμZN1)/[(λ+2μ)(ZN1+ZN2)+

4μ(λ+μ)ZN1ZN2+1]

C33=(λ+2μ+4μ(λ+μ)ZN1)/[(λ+

2μ)(ZN1+ZN2)+4μ(λ+μ)ZN1ZN2+1]

(8)

式中:λ、μ为含孔隙各向同性背景介质的拉梅系数和剪切模量。

1.3 孔隙流体

研究饱和流体裂隙孔隙介质中的波场传播，可以利用各向异性Gassmann方程[14]引入孔隙流体。当介质由单一各向同性颗粒组成的各项异性骨架时，流体饱和弹性模量和干岩石骨架弹性系数之间的关系可以用Gurevich改的各向异性Gassmann方程来表示[15]:

(9)

其中，

式中:Kg为组成岩石的各向同性颗粒的体积模量;Kf为孔隙流体的体积模量;φ是总孔隙度。

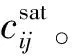
1.4 Biot模型

1.4.1 本构方程

Biot理论基于一定的假设描述了流体饱和孔隙介质中的弹性波传播。根据Biot的描述，本构方程为式(10)。

(10)

其中：ekl为固相应变；ε为液相应变；Qj表示固液之间的体积变化耦合关系；R为孔隙流体的弹性参数；σij、s分别为固、液相的应力，并且孔隙度φ及流体压力p满足,

s=-φp

(11)

1.4.2 运动微分方程

根据Biot理论，不考虑外力作用时，饱和双相介质的运动微分方程为式(12)。

(12)

式中:ρ11+ρ12=(1-φ)ρs,ρ12+ρ22=φρf，ρ12=-ρa

其中：B为耗散系数;η为流体的粘滞系数;kij为各个方向的渗透率;ρs为固相骨架密度;ρf为液相流体密度;ρa为两者之间的耦合密度。

1.4.3 几何方程

若固相位移为u，液相位移为U，在双相介质中，应力与位移的关系有

(13)

1.4.4 双相介质的一阶速度应力方程

将几何方程(13)带入到本构方程(10)，再对时间求一阶倒，得到速度表示应力的方程为式(14)。

(14)

将运动微分方程(12)化简，得到应力表示速度的方程为式(15)。

(15)

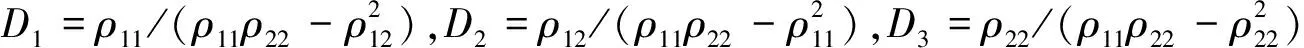
2 数值模拟

2.1 模型设置和网格参数

我们主要研究波场随着裂缝参数的变化，因此除裂缝外的参数是不变的，参数值见表1。

表1 介质参数表(不包括裂缝参数)

使用有限差分方法正演 ，震源使用雷克子波，函数如下，

e-λ[(x-x0)2+(z-z0)2]

(16)

密度单位kg·m-3，耦合参数Q1、Q3、流体参数R单位为109kg·m-1，Kf单位为Gpa，速度Vp和Vs单位为m/s

式中:f0为震源中心频率;t0=1/f0为子波延迟时间;(x0,z0)为震源中心位置;λ为震源作用的集中系数。

设计一个单层均匀的正交裂缝双相模型，模型网格数为300×300，网格大小为1 m×1 m。子波频率为20 Hz，时间采样间隔时0.1 ms。

2.2 不同裂隙参数的数值模拟

笔者使用裂隙参数为裂隙法向弱度EN和切向弱度ET。弱度参数的大小与裂隙尺度，填充物等参数相关。弱度与屈服度之间的关系为，

EN=ZN(λ+2μ),ET=ZTμ

(17)

式中:λ、μ为背景岩石介质的拉梅常数和剪切模量。

需要注意的是，文中的裂隙参数均为干裂隙参数，流体的表示是使用Gassmann方程来填充流体。在一些文章中提出EN为“0”表示流体饱和情况，实际上在高频情况下(实验室超声波测量)才满足这一条件，而本文通过Gassmann方程引入流体，表述的是低频段(地震频段)时候的饱和情况。若裂隙中没有其他固体包含物，则裂隙的法向弱度和切向弱度之比仅仅与背景介质的纵横波速度之比相关。

2.2.1 不同分量波场

按照表2的参数计算出四个分量的波场快照，如图2所示。从图2可以看出，双相各向异性介质中有三种波，传播速度最快的快qP波，呈现椭圆形，中间一圈形状复杂，有三叉区现象的波是qSV波，最内一圈是传播速度最慢的慢qP波。从流相与固相的对比中可以看出，流相的慢qP波比固相的慢qP波能量强，固相的qSV波比流相的qSV波能量强。

图2 不同分量波场快照(0.04 s)Fig.2 Snapshots of wavefields of different components(0.04 s)(a)固相速度x分量;(b)固相z分量；(c)流相x分量;(d)流相z分量

表2 模型裂隙参数表

笔者主要是分析波场特征随着裂缝参数的变化，考虑到各个分量的波形差异不大，后面只展示波场的固相速度z分量。

2.2.2 单组裂隙变化对波场特征的影响

在单组裂缝情况下，研究ET参数变化对波场特征的影响，裂缝参数的选择如表3所示。计算出的波场快照如图3所示。

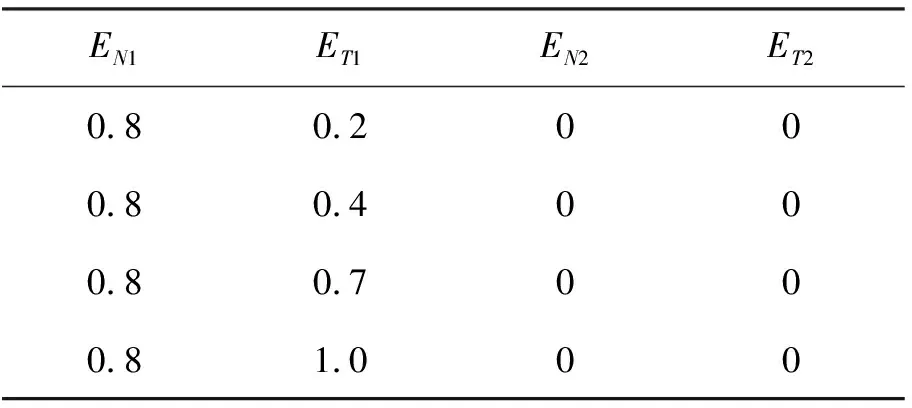
表3 单组裂隙变化裂隙参数表

从图3可以看出，随着切向弱度ET的增加，快qP波在裂缝的两侧和裂缝走向上，即水平和竖直方向上波场位置没有变化。在四个角处向内微微收敛，从跑道形态的椭圆转向偏菱形的椭圆，变化不太明显。可观察到qSV波的变化剧烈，从没有三叉区现象到三叉区现象明显。在介质的各个方向上波形缩小，速度降低。慢qP波形态变化不明显，能量加强。

图3 竖直裂隙切向弱度变化的波场快照(0.04 s)Fig.3 Snapshot of wavefields of vertical fracture tangential weakness change (0.04 s)(a)ET1=0.2分量;(b)ET1=0.4;(c)ET1=0.7;(d)ET1=1.0

2.2.3 单组裂隙变化对波场特征的影响

研究竖直裂缝模型波场随着裂缝法向弱度参数的变化，设计裂缝参数如表4所示，计算出的波场快照如图4所示。

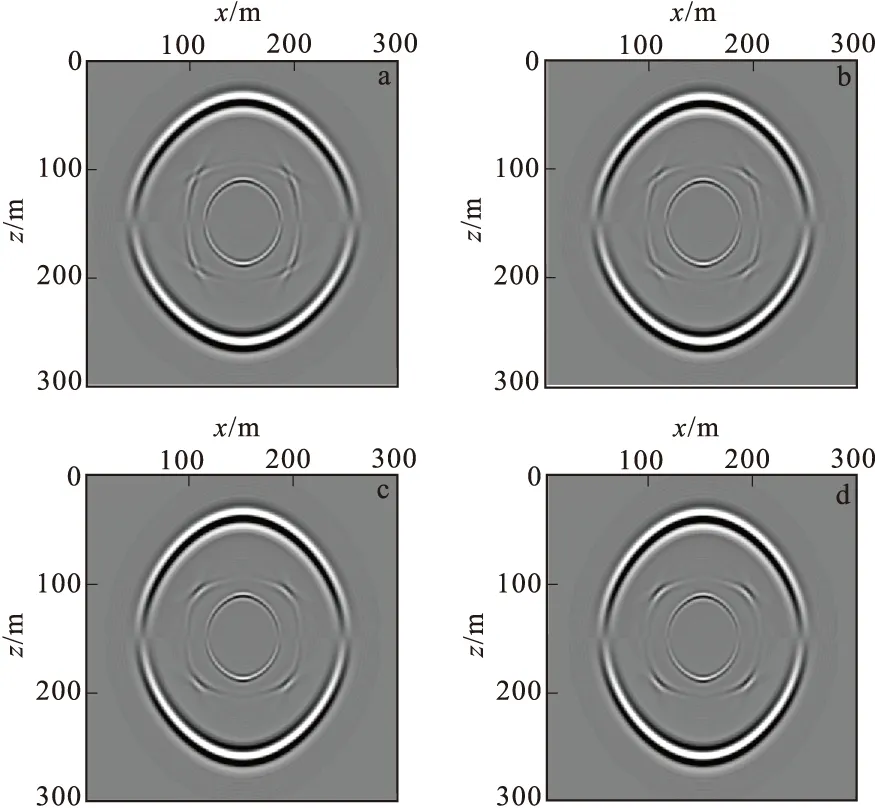
图4 竖直裂隙法向弱度变化的波场快照(0.04 s)Fig.4 Snapshot of wavefield of weakness change in normal direction of vertical fracture (0.04 s)(a)EN2=0.2;(b)EN2=0.4;(c)EN2=0.7;(d)EN2=1.0

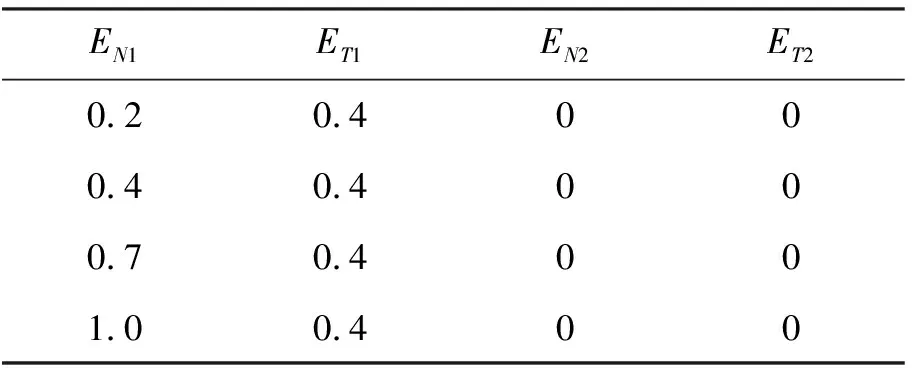
表4 单组裂隙变化裂隙参数表

从图4中可以看出，随着的增加，qSV波变化不明显，形状呈现椭圆状，存在不明显的三叉区现象，快qP波在裂缝的两侧方向向内收敛，椭圆形态加重，长轴变长，短轴变短，扁平率增加，在裂缝的走向上没有变化，传播速度不变。慢qP波变化不明显，在裂缝两侧有微弱的向内收敛。

2.2.4 正交裂隙变化对波场特征的影响

在正交裂缝情况下，研究波场快照随着裂隙切向弱度的变化。两组裂隙的参数值相同，具体参数见表5，计算出的波场快照如图5所示。

表5 正交裂隙变化裂隙参数表

图5 正交裂隙模型切向弱度变化的波场快照(0.04 s)Fig.5 Wavefield snapshot of tangent weakness change of orthogonal fracture model (0.04 s)(a)ET=0.1;(b)ET=0.3;(c)ET=0.6;(d)ET=1.0

从图5中可以看出整体上，在ET较小的时候，三叉区现象明显，位于四个坐标轴方向，如图5(a)所示；随着ET增加，三叉区现象减弱，然后再增强，此时的三叉区位于坐标轴的四个近似45°角处。快qP波在水平和竖直方向上波场位置没有变化，在四个角处向内微微收敛。qSV波变化剧烈，各方向的速度降低，波形缩小；三叉区现象的位置改变，从四个正方向到四个斜方向。慢qP波形态变化不明显，能量加强。

2.2.5 正交裂隙变化对波场特征的影响

在正交裂缝情况下，研究波场快照随着裂隙法向弱度的变化。裂隙参数见表6，计算出的波场快照如图6所示。

图6 正交裂隙模型法向弱度变化的波场快照(0.04 s)Fig.6 Snapshot of wavefield of normal weakness change of orthogonal fracture model (0.04 s)(a)EN=0.2;(b)EN=0.5;(c)EN=0.8;(d)EN=1.0

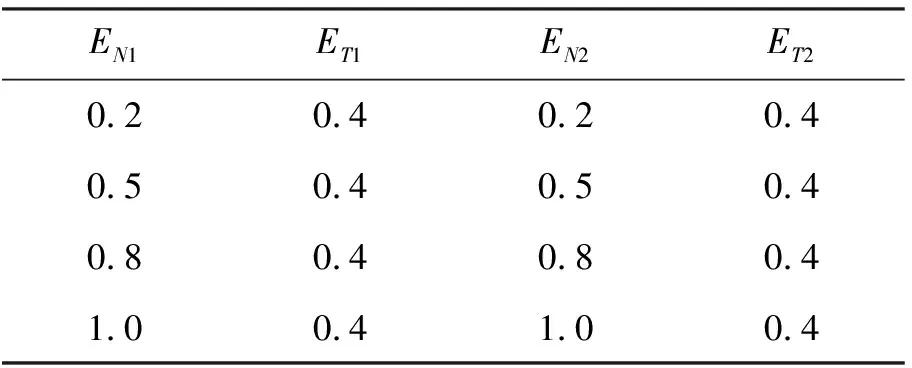
表6 正交裂隙变化裂隙参数表

从图6中观察到，快qP波在形态上都近乎椭圆，随增大，椭圆缩小，形成较为标准的圆形。快qP波各个方向的速度降低。qSV波在水平和竖直方向上波场位置没有变化。在四个角处的三叉区现象消失，波形向内靠。形态上从不规则到椭圆状态。慢qP波形态变化不明显，振幅增强。

从图3到图6，慢qP波的形态变化都不大，说明裂隙参数对慢qP波的影响较小。

2.2.6 裂隙密度对波场特征的影响

在上面的一些规律分析中，裂缝参数比较抽象，且各别极端情况并不会出现。笔者只讨论一种具体的情况，波场随着裂隙密度的变化的规律。从Hudson理论中，当裂缝为椭球体裂缝时，不含包含物的干裂缝弱度计算公式为：

(18)

按照本文设计的参数，计算出裂隙弱度参数随着裂隙密度的变化，如图7所示。法向弱度和切向弱度随着裂缝密度线性增加。法向弱度相对于切向弱度随裂隙密度的变化更敏感。这表明在做裂缝预测工作时，可以更多的关注法向弱度这个参数。

图7 弱度随裂缝密度变化曲线Fig.7 The curve of weakness-fracture density

按照不同的裂隙密度，计算出波场快照，单组裂隙模型如图8，正交裂隙如图9所示。

图8 单组裂隙波场随密度变化快照(0.04 s)Fig.8 Snapshot of the wavefield of a single group of fractures changing with density (0.04 s)(a)e=0.01裂缝密度;(b)e=0.05;(c)e=0.10;(d)e=0.15

图9 正交裂隙波场随密度变化快照(0.04 s)Fig.9 Snapshot of orthogonal fracture wavefield changing with density (0.04s)(a)e=0.01裂缝密度;(b)e=0.05;(c)e=0.10;(d)e=0.15

从模拟结果来看，单组裂缝时，快qP波在裂缝两边向内收敛，从圆形变为椭圆；qSV波，各方向的速度降低，波形缩小，裂隙密度增大到一定程度，出现较弱的三叉区现象；正交裂缝时，qSV波和快qP波的形态近乎圆形，随着裂隙密度增加，圆形缩小。

3 结论与展望

笔者使用线性滑动理论和各向异性Gassmann方程，构建饱和的正交裂缝孔隙型介质，然后使用高阶有限差分对我们构建的正交模型进行数值模拟，并取得了以下几点认识：

1)裂缝参数的变化对慢qP波的形态影响不大，但裂缝参数值增大，慢qP波能量增强。

2)EN变化对快qP波影响大。对qSV波的影响小；ET变化对qSV波影响大，对于快qP波而言，主要是影响除切向法法向以外的速度。

3)在单组裂隙中，随着ET越大，三叉区现象约明显。随着EN的增加，快qP波的椭圆形态加重。

4)在两组裂隙参数相同的正交裂隙介质中，随着ET增加，qSV三叉区现象从四个坐标轴方向逐渐消失，然后再出现在坐标轴的四个近似45°角处。EN增加，快qP波缩小，形态趋近于标准的圆形。

在实际的地震勘探中，主要还是应用纵波勘探。通过本文的研究，纵波主要受到裂隙法向弱度的影响。若不考虑裂隙中含有其余固相颗粒，则对裂隙密度更为敏感，也就是对裂隙发育更敏感。这表明对于地下裂隙的预测，我们可以更多地关注如何从纵波地震数据中反演出裂隙法向弱度参数。