DS-CDMA中盲多用户检测算法的研究与性能分析
2022-01-06钱雅儒
雍 慧,钱雅儒,马 毅
(1.宁夏回族自治区无线电管理委员会办公室,宁夏 银川 750000;2.中国移动宁夏公司银川分公司,宁夏 银川 750000)
0 引言
在DS-CDMA系统中,当多个用户的信息在同一个信道中传输时,利用扩频码的不同来区分,用户之间因非理想正交化产生非零互相关值,从而造成多用户干扰(MAI),很大程度上限制了系统容量并造成通信解码时误码率大幅度上升,甚至无法通信。多址干扰会导致“远近”效应问题从而进一步的恶化系统性能。所以在CDMA通信系统中,通信最关键的一个技术就是解决信号的多址干扰问题和抗“远近”效应等,目前多用户检测已成为有效抑制多用户干扰的一个主要措施。这些算法需要知道干扰用户的扩频码知识、发送训练序列等较多的先验信息;且复杂度随用户码元数呈指数率增加;特别的,信道和用户数是时变的,要不断发送的训练序会占用大量的系统资源。
因此,只需知道目标用户的扩频波形,而不需要知道具体训练序列的盲多用户检测技术逐渐成为目前研究的热点。本文对3种基于最小均方算法(Least Mean Square, LMS)和递归最小二乘算法(Re-cursive Least-Square, RLS)以及Kalman滤波盲多用户检测算法的误码率、信干比与算法的计算复杂度进行了比较分析,为后期研究多用户检测算法性能的改进和提高提供了参考。
1 系统模型
在加性高斯白噪声信道环境下,K个用户的同步CDMA系统,接收端的基带信号可表示为:

式中,Ak表示第k个用户信号幅度;{bk(i)∈{-1,+1}}为第k个用户发的信息序列;Tb为信息符号的间隔;n(t)是具有单位功率谱密度的高斯白噪声;σ是高斯白噪声的均方误差;sk(t)是第k个用户的归一化特征波形。
设用户1为期望用户,则接收到的信号可表示成:

式中,r=[r(0),r(1),…,r(N-1)]T为接收信号向量;Sk=[Sk(0),Sk(1),…,Sk(N-1)]T为特征波形向量;v=[v(0),v(1),…,v(N-1)]T是噪声向量。式(2)右边的 3项依次代表期望的用户信号、所有其他干扰用户的信号之和、信道的噪声。
2 盲多用户检测的典范表示
假设用户1为所期望的用户,探讨用户1的线性多用户检测器,使决策统计量
盲多用户检测器的典范表示有两种:


3 盲多用户检测原理及方法
盲多用户检测思想:只根据一个码元间隔内的r=[r(0),r(1),…,r(N-1)]T和sk=[sk(0),sk(1),…,sk(N-1)]T,即可估计期望用户的发送序列bk(n)。所谓“盲”是不需要其他用户的任何信息。目前典型的盲算法中主要有:最小均方(LMS)算法、递归最小二乘(RLS)算法及卡尔曼(Kalman)滤波算法。
3.1 LMS算法的盲自适应多用户检测
LMS算法核心思想就是在迭代基础上用平方误差作为均方误差值的估计值。在盲多用户检测中,考虑利用典范表示1描述的盲多用户检测器c1,则其输出信号

假设用户1为待检测用户,则其线性检测器为:c1=s1+x1,其中分量是恒定不变的,分量x1是不断更新的权矢量,并且x1和s1是正交的,即x1Ts1=0。所以检测器的更新设计就相当于x1的更新,x1的选取应该实现此线性检测器输出能量值最小化,来达到减小干扰的目的。
盲自适应多用户检测的LMS滤波算法流程如图1所示[1]:

图1 盲LMS算法流程
其中,迭代步距μ必须要满足使输出均方误差收敛的稳定性条件。

式中,N为扩频增益;σ为背景噪声。
3.2 RLS算法的盲多用户检测
RLS算法核心思想是最小化盲检测器的指数加权输出能量,利用指数加权的平方和代替了LMS算法的最小均方准则。从而得到下面最优化的约束问题:

约束条件为:

式中,0<λ<1为遗忘因子,λ可以使得过去时间比较久的数据的权重得到相应减小,以至于降低它们的影响。盲自适应多用户检测的RLS算法流程[2]如图2所示:
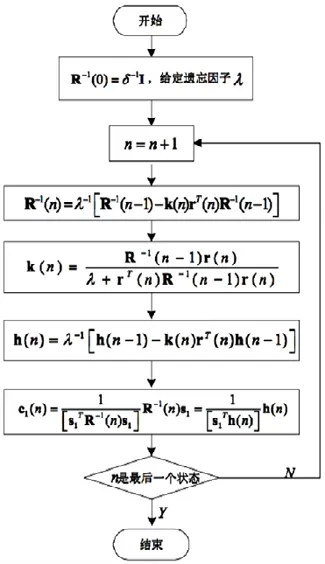
图2 RLS盲多用户检测算法流程
3.3 基于Kalman滤波算法的盲多用户检测
按照多用户检测的原理,建立一个多用户检测器的状态空间模型,通过采用Kalman滤波算法来估计出最优的判决向量,这便是基于Kalman滤波的盲多用户检测算法。
根据线性检测器的典范表示2,得到对于待检测用户k的判决向量ck(n)可以表示为(n),式中,向量wk(n)是ck(n)的自适应部分;sk是非自适应的部分。>=0,那么权向量ck(n)的自适应和非自适应两个部分正交。当sk以Ck,null已知的时候,可以自适应的更新ck(n)。Ck,null可以通过正交化方法来获得,比如斯密特或者奇异值分解方法。
对于一个时不变的CDMA系统,建立多用户状态空间模型:

盲多用户检测的卡尔曼滤波算法描述如下:已知观测方程矩阵dH(n),使用观测的数据对状态矢量wklopt的各个系数在每个n≥1时进行最小均方误差估计。
用于时不变系统的盲自适应多用户检测的Kalman流程如图3所示[3]:

图3 时不变系统的盲自适应多用户检测的Kalman流程
4 仿真结果及分析
对LMS盲多用户检测算法、RLS盲多用户检测算法和Kalman滤波盲多用户检测算法在平稳信道即加性高斯白噪声信道环境中进行实验仿真,并对它们相互之间的性能差异进行对比。为对比不同算法抗多址干扰的能力,仿真实验选择系统时间平均信干比(SINR)与时间平均的剩余输出能量(EOE)作为性能指标。
考虑10个用户同步CDMA系统的多用户检测问题,采用BPSK方式调制,以n=5的Gold序列作为扩频序列,扩频增益取N=31,传输数据数目为2 000,以用户1作为待检测用户。假定用户k的信噪比, 其中,Ek=A2k为用户k的比特能量;所期望用户1具有单位能量,即:A21=1,信噪比为20 dB,背景噪声方差σ2=0.01;多址干扰用户9个,其中有3个干扰用户信噪比均为30 dB其中1个干扰用户的信噪比为50 dB(即A25=1000),其中5个干扰用户信噪比均为40 dB在运行LMS算法时,本次仿真试验的步长因子设定为μ=10-5。使用RLS算法时,初始值R-1(0)=δ-1I,取δ=0.01,遗忘因子λ=0.997。
(1)静态环境仿真:在高斯白噪声信道环境下,对同步CDMA系统采用LMS算法、RLS算法和Kalman滤波算法三种算法迭代2 000步,独立运行500次。仿真过程中没有其他干扰用户加入或撤出。仿真结果如图4所示。LMS和RLS算法分别在迭代500次和700次之后开始收敛,并且分别稳定在11 dB和13 dB左右,Kalman算法随着迭代次数增加其SINR值一直递增,2 000次时接近18 dB。由上分析说明,Kalman算法的抗干扰能力比其他两种算法明显要强,Kalman滤波算法的收敛速度比LMS算法和RLS算法的要快。

图4 (a) 时间平均信干比曲线
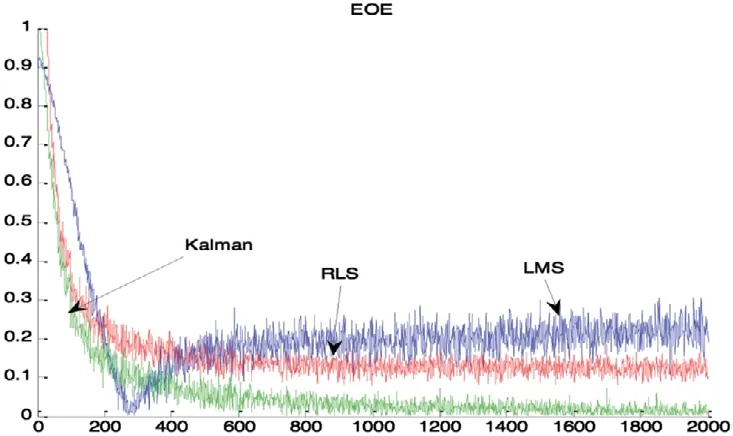
图4 (b) 剩余输出能量曲线
(2)动态环境下仿真:与静态环境仿真的初始条件是相同。分别考虑下面的四种动态环境,基本涵盖了实际情况下的动态环境,比较符合实际的动态通信系统。
①迭代600次时先加入3个40 dB的干扰用户,迭代1 200次时再移除2个40 dB的干扰用户和1个 50 dB的干扰用户;②迭代600次时先加入2个40 dB的干扰用户,迭代1 200次时再加入1个40 dB的干扰用户和1个50 dB的干扰用户;③迭代600次时先移除4个40 dB的干扰用户,迭代1 200次时再加入3个40 dB的干扰用户和1个50 dB的干扰用户;④迭代600次时先移除2个40 dB和1个50 dB的干扰用户,迭代1 200次时再移除1个30 dB的干扰用户。
实验仿真结果如图5所示:三种算法都有收敛跟踪能力,只是LMS的收敛跟踪新性能稍差一些。在用户动态变化是,LMS算法SINR提高不明显,LMS算法EOE值随动态用户变化很大,曲线存在严重的抖动;RLS和Kalman都有收敛递增的趋势,但后者递增趋势更大,且稳定后SINR值更高,基本不受干扰用户的影响,能够在非常小的抖动后再次迅速收敛,但是RLS算法在系统用户改变的时候跳变的非常明显,而Kalman滤波算法能够一直保持很好的剩余输出能量,稳态的情况下接近于零值。所以,LMS算法易受到时变传输环境的影响,而Kalman算法抗干扰能力很强。
比较LMS,RLS和Kalman三种算法的计算复杂度(每个码元间隔之内,更新抽头权矢量c1(n)的计算量)。
LMS算法[4]:4N次乘法和6N次加法;
RLS算法[1]:4N2+7N次乘法和3N2+4N次加法;
Kalman算法[5]:4N2 -3N次乘法和4N2 -3N次加法。

图5 (a) 四种动态环境下的时间平均信干比曲线

图5 (b) 四种动态环境下的剩余输出能量曲线
所以,三种算法各有优点和不足:LMS算法编程相对简单,算法复杂度较低,然而收敛速度很慢,且跟踪信道变化能力较差。RLS算法和Kalman算法的收敛速度较快,抗干扰能力强,能够更快地跟踪信道变化,但是算法复杂度明显增高。特别是Kalman算法有更快地收敛速度和更高的信干比,在硬件满足的条件下更加实用。
