杆式杀伤元可控飞散技术研究*

张亮，毛川，李川，李俊龙，高位，陈华文，何有为

(重庆红宇精密工业集团有限公司，重庆 402760)

0 引言

随着导弹制导技术的进一步发展，国际上新型杆式战斗部研究与设计异常活跃[1]。Raytheon公司分析认为[2]，如果在直接撞击式导弹上加装杆式战斗部，当导弹系统确定来袭导弹己经处在直接撞击的致命毁伤区域之外时，迅速起爆杆式战斗部，可以获得高得多的毁伤概率，对巡航导弹和飞机等目标有着更好的毁伤效果。离散杆战斗部与破片式战斗部相比，杀伤元素质量大，杀伤效率高，对空中目标的切割能力强、破坏力大[3]。离散杆战斗部具有破片战斗部杀伤半径大、破片速度高的特点，而且单杆对空中目标的破坏力远远大于单枚破片的破坏力，同时它的杀伤半径又大于连续杆[4]。

李华新等从理论分析、试验研究対聚焦型离散杆战斗部爆炸驱动及飞行规律进行了研究[5]。赵英杰等介绍了离散杆式战斗部结构及杀伤原理，推导了杀伤概率的主要因素[6]。张雄飞、李卫青等在飞行力学和空气动力学基础上对杆条运动进行了初步分析[7-8]。刘志建等探索性提出可控离散杆工程设计方法[9-10]。孙传杰等利用Shapior理论并结合数值仿真对离散杆式战斗部飞行控制的设计方法进行了探索[11-14]。对杆式杀伤元爆炸驱动可控技术研究，是单层可控离散杆战斗部的关键技术，以上研究过程中都假设杆条为刚性体，没有考虑到杆条变形防护是姿态可控基础，杆式杀伤元完整性控制方法是可控离散杆战斗部设计急需解决的问题。

1 杆式杀伤元飞散姿态控制

按照Shapior理论，爆轰波是由战斗部扩爆药O点出发，以球形波阵面的形式向外传播，杆式杀伤元端部的法线与产品轴线构成夹角φ1，爆轰波阵面法线与产品轴线构成夹角φ2，产品微元速度矢量偏离杆式杀伤元法线的偏角为θ。可控杆式杀伤元产品杆式杀伤元旋转的理论分析见图1。

图1 可控杆式杀伤元速度分析图Fig.1 Velocity analysis diagram of controllable rod-type killing element

图1a)中，产品在端面O起爆后，通过对另一端面杆式杀伤元微元的速度分析，可以发现杆式杀伤元端部存在一个侧向速度分量，这个侧向速度分量即为杆式杀伤元侧向旋转的初始线速度。从速度分解可得到v0C为

(1)

式中：v0为杆式杀伤元端部微元飞散初速(m/s)；l为杆式杀伤元长度(mm)；de为装药直径(mm)；θ为杆式杀伤元端部微元飞散偏转角(°)；α为杆式杀伤元与产品轴线的夹角(°)。

由此可见，杆式杀伤元装配与产品轴线有一个夹角α时，产品爆炸后，在爆轰波的作用下，杆式杀伤元在向外飞散的同时还会产生旋转。旋转方向由下式决定：

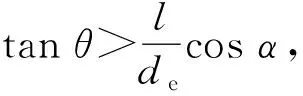
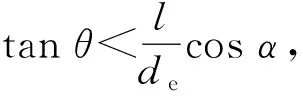
产品爆炸后，假定杆式杀伤元质心运动为径向直线运动，则杆式杀伤元飞行时间为[15]

(2)

式中：t为杆式杀伤元质心径向运动时间(s)；α为杆式杀伤元速度衰减系数(1/s)；v0为杆式杀伤元径向飞散速度(m/s)；R为杆式杀伤元飞散距离(m)。

假定杆式杀伤元的旋转为绕其质心的匀速运动，当杆式杀伤元飞行到确定的距离R时，控制旋转90°，则杆式杀伤元旋转的线速度为

(3)

由式(1)和(3)，由于α很小，近似取cosα=1，当n=0时有[16]

(4)

2 杆式杀伤元完整性控制

通过杆式杀伤元飞散姿态控制研究，其理论是在假设杀伤元为刚体结构时的空间运动规律，再考虑实际产品的结构，杆式杀伤元将发生一定变形，不利于飞行控制，需要通过结构优化实现，也就是杆条的完整性控制，通过调整杆式杀伤元上的压力分布或者说杆式杀伤元上速度矢量的分布及能量匹配等实现杆式杀伤元完整性。减少杆式杀伤元的变形是可控离散杆设计的重要环节。

2.1 杆式杀伤元完整性的理论分析

设计可控杆式杀伤元产品时，将杆式杀伤元各段微元速度差控制在一定的范围内能有效控制杆式杀伤元的弯曲变形。经过进一步分析得到，当任意相邻微元之间的初始速度差值为在某范围内的一恒值，即所有微元的初速值在“速度-微元”坐标系中为一条直线时，更有利于实现对杆式杀伤元弯曲变形的控制。考虑到工程应用，基本上无法达到一条直线。但杆式杀伤元本身是有一定的刚性的，杆式杀伤元各个微元不是独立存在的，是相互关联的。只要控制其在一定范围内，就可以很好解决杆式杀伤元的变形问题。

在初始计算时，给定第1个微元初速v0x1，同时给定相邻微元间的速度差值Δv，由

v0xn-v0x(n-1)=Δv,

(5)

可计算出每段微元速度v0x1,v0x2,…,v0xn。

由格尼公式：

(6)

由式(6)变换得

(7)

则每段微元所对应的装填比β(x)可由式(6)计算得到。

实际设计可控杆式杀伤元产品时，可调整每段杆式杀伤元微元对应的装填比等于理论计算给定装填比β(x)，使每段微元的速度等于给定的速度v0x1,v0x2,…,v0xn。

2.2 杆式杀伤元完整性的仿真分析

在控制杆式杀伤元完整性控制的研究中，进行了ANSYS/LS-DYNA数值仿真，采用了单点(LS-DYNA单元11)算法。由于炸药爆炸后爆轰气体直接作用于杆式杀伤元上，采用拉格朗日算法不能保证爆轰气体和杆式杀伤元之间的正常接触，因此进行数值仿真时采用了ALE(arbitrary Lagrangian-Eulerian)多材料算法。即炸药四周充填空气介质，炸药和四周的空气介质均被剖分成欧拉(Euler)网格，杆式杀伤元、壳体、前盖和后盖均被剖分成拉格朗日网格，并置入欧拉网格中。为了消除边界效应，空气介质的外边界设置成压力输出边界以表示无限欧拉场。计算时将拉格朗日网格完全放在欧拉场中，程序采用一定的耦合方式表示拉格朗日网格和欧拉空间之间的相互作用。拉格朗日介质之间采用自动单面接触(LS-DYNA接触类型13)模拟结构之间的相互作用。

计算初始条件：

装药结构：内径φ65 mm，外径φ105 mm，长度185 mm，B炸药；杆式杀伤元参数：φ4 mm×150 mm，80根，低碳钢；壳体参数：内径φ115 mm，外径φ120 mm，2A12；前后端盖：厚3 mm，2A12。

按照上述的基本条件，进行参数调整，计算方案如下：

计算1：验证杆式杀伤元上速度分布具有一定速度差时，杆式杀伤元变形不大。

杆式杀伤元左端：铣削斜面长度15 mm，斜面高度1.5 mm；杆式杀伤元右端：铣削斜面长度36 mm，斜面高度1.5 mm，杆式杀伤元上速度分布虽然150 m/s差别，杆式杀伤元变形仍然不大。见图2。

图2 杆式杀伤元上速度分布及变形情况示意图Fig.2 Schematic diagram of velocity distribution and deformation on rod

计算2：验证实心装药与空心装药对杆式杀伤元变形的影响。

图3a)为实心装药杆条变形，变形长度约为杆条长度的30%；图3b)为空心装药杆条变形情况，杆条基本未变形。因此，在可控离散杆设计时，尽量采用空心装药结构。

(3) 控制方法

方法1：可控杆式杀伤元通过空心装药，减少径向装药量，调整装填比，将杆式杀伤元速度控制在1 800 m/s 以内，可以控制杆条变形。

图3 实心装药和空心装药的杆式杀伤元变形情况对比Fig.3 Comparison of the deformation of rod of solid charge and hollow charge

方法2：改变微元对应段驱动质量。就是改变杆式杀伤元的质量分布，常采用杆式杀伤元两端铣削斜面，通过改变杆式杀伤元质量分布达到改变驱动比，提高杆式杀伤元两端速度，降低速度差。此种方法结构简单，但杆式杀伤元两端斜面不易铣削过大，过大将产生杆式杀伤元端部弯曲的情况，如图4所示，杆条端部铣削斜面位置杆条强度降低，发生严重弯曲。

图4 杆式杀伤元端部弯曲情况Fig.4 End bending condition of rod

方法3：改变微元对应段装药厚度。这即是工程试验时用来控制杆式杀伤元弯曲变形的另一种设计方法。当产品直径较小时，由于受到产品结构限制，考虑到装药量的关系，其中心管不能过大，只调整杆式杀伤元两端斜面，无法达到调整杆式杀伤元上速度分布的作用，此时就可以调整中心管空腔或装药形状，实现调整杆式杀伤元上速度分布的目的。

在杆式杀伤元设计时，3种调整方法可以综合使用，具体情况需要由实际结构来决定。

3 试验验证

3.1 试验参数设计

杆式杀伤元采用φ4×150 mm圆形杆，采用设置中心管和调整杆式杀伤元两端铣削斜面控制杆式杀伤元的变形，达到杆式杀伤元上速度分布均衡的目的，杆式杀伤元安装斜置角2°，试验件采用端面起爆。测试杆条在不同距离处旋转角度，验证设计方法的正确性。试验件结构示意图如图5所示，具体结构参数如表1所示。试验产品数量1发。

图5 试验件结构示意图Fig.5 Schematic diagram of test piece structure

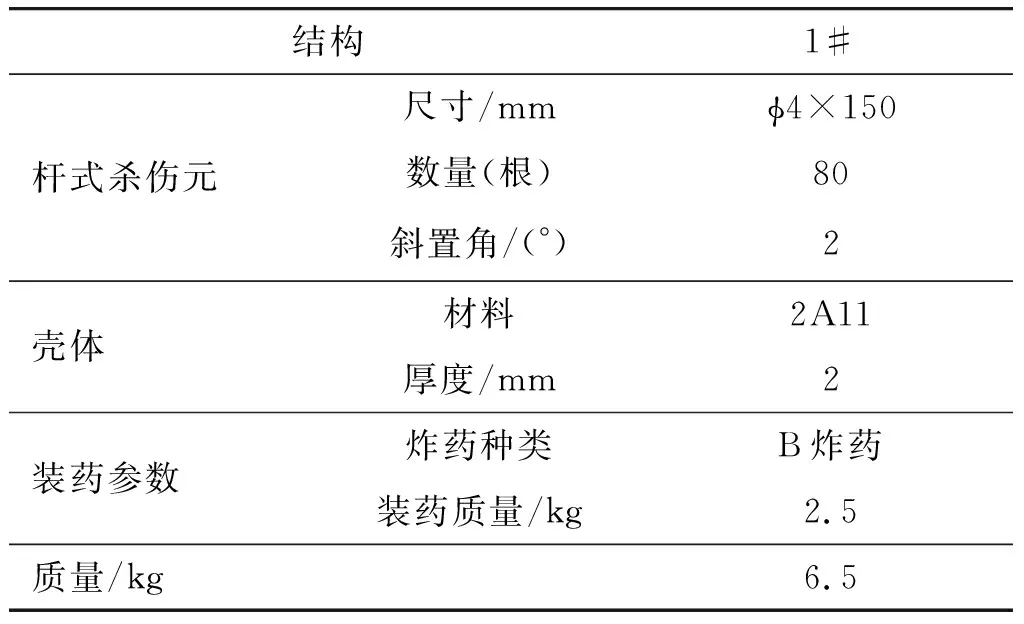
表1 产品结构参数表Table 1 Test piece structural parameters table

3.2 靶场布置

试验件立放在托弹架上，在距爆心2,3,3.5,4 m处布置靶板，测试杆式杀伤元飞散姿态，布置断靶网2路，每路由4个靶网组成，测试杆式杀伤元初速。具体布置图见图6。

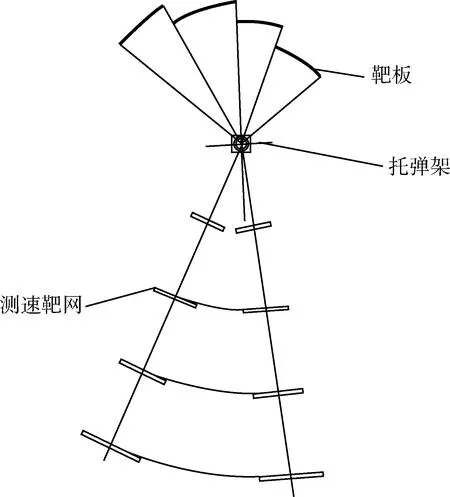
图6 靶场布置图示意图Fig.6 Schematic diagram of test site

3.3 试验结果

杆式杀伤元在靶板上的穿孔情况见图7～10。

图7 2 m处靶板穿孔情况Fig.7 Target perforation at 2 m position

图8 3 m处靶板穿孔情况Fig.8 Target perforation at 3 m position

图9 3.5 m处靶板穿孔情况Fig.9 Target perforation at 3.5 m position

图10 4 m处靶板穿孔情况Fig.10 Target perforation at 4 m position

将设计计算结果与试验件试验测试结果进行对比，对比结果见表2。

表2 设计与试验结果符合性统计表Table 2 Conformity comparison table of design and test results

通过对比分析杆式杀伤元的初速、飞行姿态、方向角与工程计算相当，工程计算可以指导产品设计，并且杀伤元变形不大，说明控制方法有效。

4 结论

本文研究了杆式杀伤元旋转机理，探讨了杆式杀伤元飞散控制，分析了斜置角对杆式杀伤元飞行性能的影响，提出了杆式杀伤元完整性控制。调整杆式杀伤元上的压力分布或者说杆式杀伤元上速度矢量的分布及能量匹配等实现杆式杀伤元完整性，减少杆式杀伤元的变形。并通过试验研究，验证了杆式杀伤元完整性及飞行可控性。得到如下结论：

(1) 给出了杆式杀伤元初速、杀伤半径、杆式杀伤元斜置角三者之间的关系。

(2) 进行了杆式杀伤元完整性控制设计，提出了控制方法，并通过试验设计和验证，得到了有效的试验数据。结果与理论设计分析和数值仿真结果相吻合，说明建立的理论分析是正确的，建立的控制模型是可靠的。