基于LMS算法的自适应滤波器性能分析*

刘建涛 席 闯 姜海洋

（沈阳辽海装备有限责任公司 沈阳 110000）

1 引言

滤波器研究的目的是设计和制造最佳的（或最优的）滤波器，减小期望频率信号的衰减，并阻止非期望频率信号通过，分为传统与现代滤波器，可通过软件或硬件实现［1］。本文将比较三种经典滤波器的滤波性能，并重点介绍LMS自适应滤波器的实际应用。

2 滤波器原理

2.1 经典滤波器

20世纪40年代，数学家维纳（Norbert Wiener）首次提出噪声是叠加于信号之上的，即加性噪声的概念：

其中，x(t)为实测值；s(t)为目标信号；v(t)为噪声信号。

为了还原目标信号，就需要进行滤波。其中模拟滤波器只能粗略的限定可通过的信号的频率范围，更进一步的滤波、平滑甚至预测等任务需要交给数字滤波器来处理，以下提及的滤波器均指代数字滤波器。

在离散数字信号的场合，设y(n)为期望输出，有：

一个典型的滤波系统具有如下结构［2］：

图1 滤波器组成

其中，ℎ(n)为冲激响应。

但由于滤波器自身性能的限制，以一个线性滤波系统为例，其实际输出为

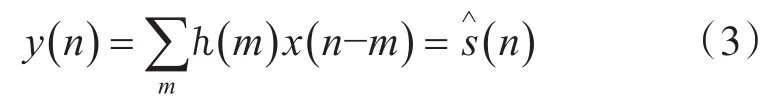
2.2 维纳滤波器

依据最小均方误差准则，希望求得误差值平方的期望值最小。设误差e(n)，真实值s(n)，估计值，即：

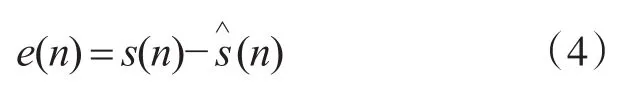
最小均方误差为

设冲激响应h（n），有：

式中，Rxs(m)为互相关函数，Rxx(m)为自相关函数，即：

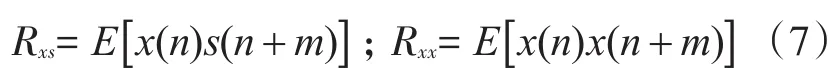
若这两个参数已知，即可由式（6）求得滤波器系统冲激响应。

2.3 卡尔曼滤波器

卡尔曼滤波器的描述建立在这样一个状态空间基础上：即认为系统噪声和测量噪声共同引起了实际误差，系统框图如下：

图2 卡尔曼滤波系统

由其思想可以看出，卡尔曼滤波器是在观测值和估计值之间进行折中。当估计误差较大时更依赖观测值，当上一次误差较小时便增加H的权重。

2.4 LMS自适应滤波器

LMS自适应滤波器同样采用最小均方准则，系统的闭环结构使其更适用于信号模型未知的情况，该系统结构如下［3］：

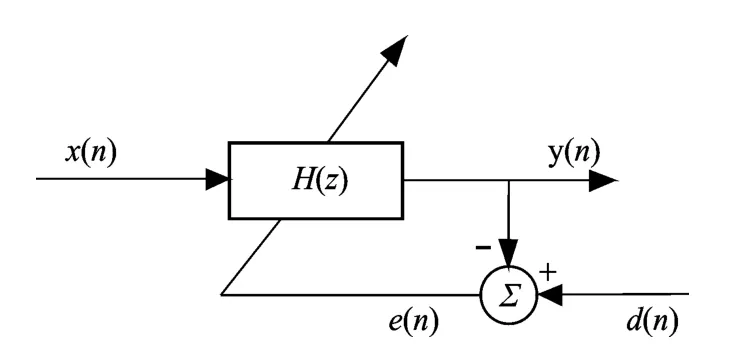
图3 自适应滤波器的结构

图中，x(n)为输入；y(n)为输出；H(z)为参数矩阵；d(n)为期望；e(n)为误差。通过e（n）对数字滤波器进行重新设置，使误差的均方插值最小。

当n时刻的输入x(n)进入到滤波器时，M阶滤波器输出为

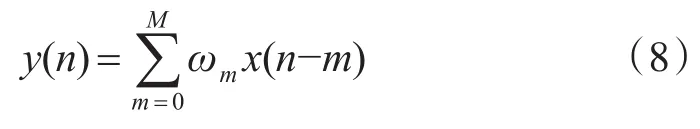
其中ωm为第m个抽头线上的权值。

对ωm的自适应控制详细结构如图4所示。

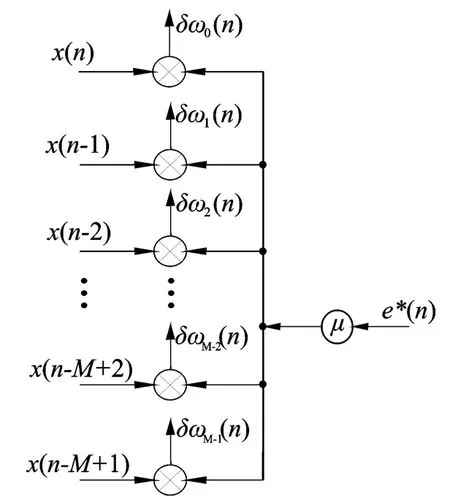
图4 权值自适应控制算法模型

图中，μ为步长因子（也称收敛因子）根据上图，有：

w为ω的向量形式。

μ的取值范围为

式中SMAX为x（n）功率谱密度的最大值。步长过大会降低滤波的精度，当μ取较小值时，LMS自适应滤波过程进行的较慢，但减少了失调的影响［4～6］，需根据实际应用场景进行调整。

3 性能分析

3.1 仿真分析

为了检验两种滤波器算法在去噪应用中的滤波性能，利用Matlab对维纳滤波器和自适应滤波器进行模拟仿真实验。仿真结果如下：

以单位幅值正弦波信号叠加高斯白噪声为例，维纳滤波器阶数为100，相关信号长度为100时，结果如图5所示。

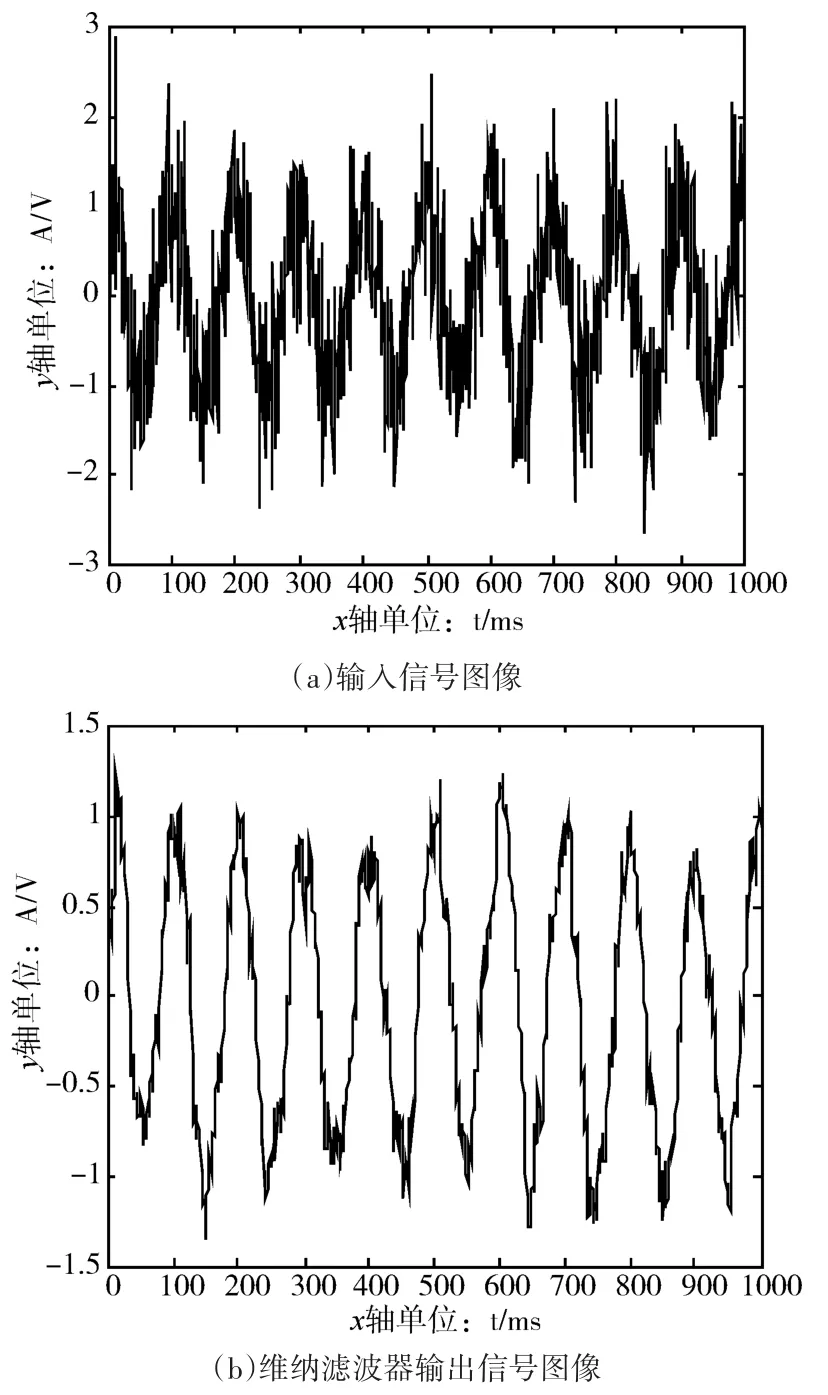
图5 维纳滤波器仿真

LMS自适应滤波器阶数为50时，结果如图6所示。

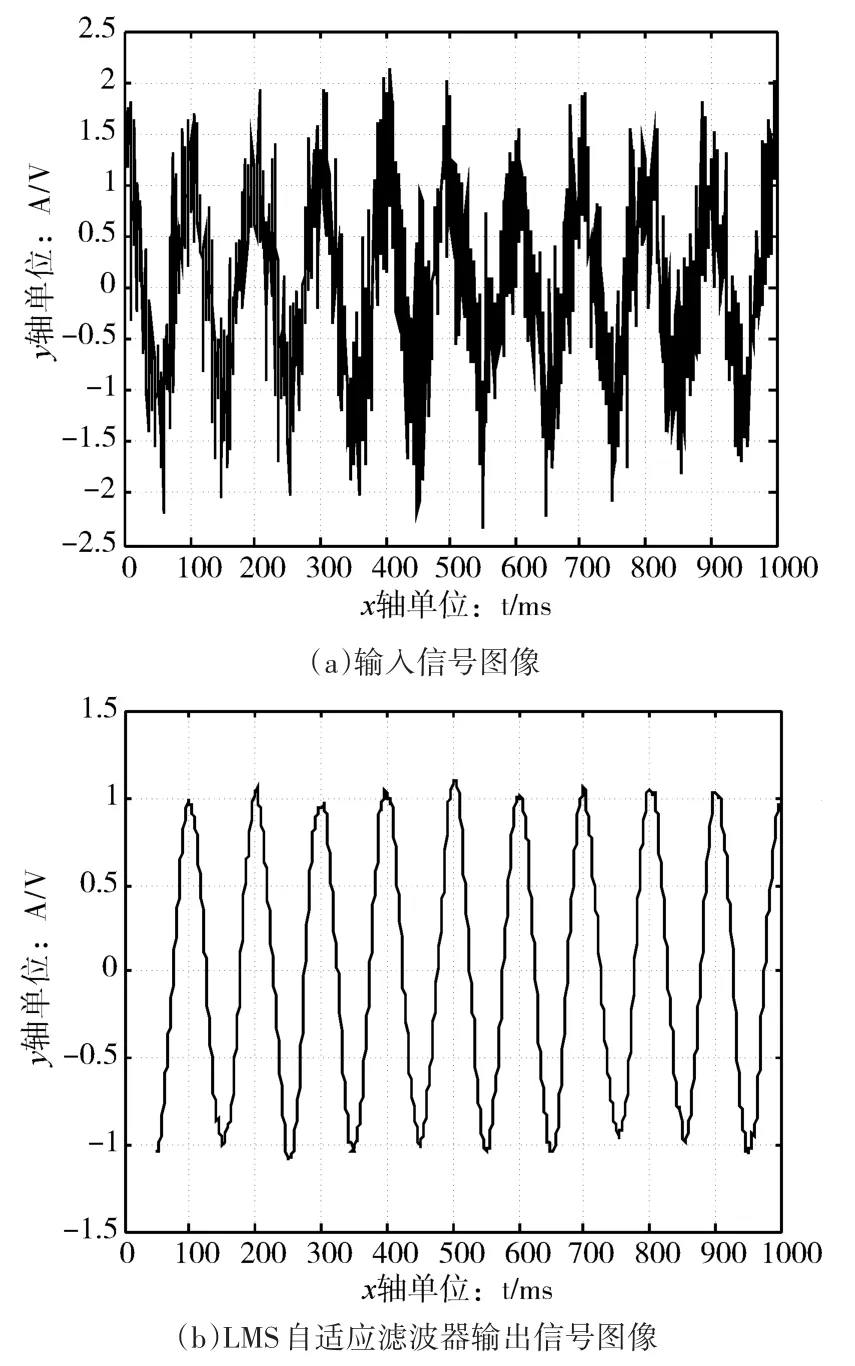
图6 LMS自适应滤波器仿真

比较上述维纳滤波器滤波结果可见，基于LMS算法的自适应滤波器对变化的信号反应更加灵敏，输出曲线相较维纳滤波器更加平滑，滤波效果更佳。图中未示出LMS自适应滤波器在前50个点的输出，这是因为当滤波点数小于阶数时，不能完全发挥出滤波器的能力。LMS自适应滤波器的输出与期望较为接近，与输入信号相比，获得了十分明显的滤波效果，输出与期望的误差的绝对值也会随信号幅值的增加而增加。

3.2 水池实验

为更直观观察LMS自适应滤波器的滤波效果，进行水池单频信号的接收实验，通过LMS自适应滤波器对接收信号进行滤波，结果如图7所示。

图7 实验滤波结果及误差

图7可直观看出，当期望信号已知时，随累积观测时长增加，LMS自适应滤波器的估计误差减小，滤波效果变好。

4 自适应LMS算法的应用

4.1 自适应均衡

避免多途影响系统性能，采用自适应均衡技术，对接收信号进行自适应均衡补偿处理，尽可能接近期望信号，消除码间干扰，解决传输环境不理想带来的失真问题［7～9］。

4.2 语音处理

不同环境噪声具有不同特性，需在已知语音信号频谱范围条件下，设计自适应滤波器，针对未知环境消除噪声干扰。基于LMS算法的自适应滤波器在语音信号处理中，具有较好的收敛性和良好的环境适应性，并且稳态误差小，广泛应用于语音系统中。

4.3 自适应回声消除

电话回声和声学回声是降低通信系统通话质量的主要原因［10］。LMS算法的快速收敛特性，可保证语音系统的实时性，是其在回声消除领域有广泛的应用先决条件之一。通过对回声路径的自适应分析，结合语音信号的自适应处理，可以有效抑制回声，降低回声信号被察觉的可能性，实现即时语音回声自适应消除。

4.4 自适应干扰对消

LMS算法收敛速度快，稳定性高，结构简单等优势，使其在需要干扰对消的军事、医疗、科研生产等方面，均有广泛的应用，例如天线阵列旁瓣对消、雷达干扰对消、降低设备电源干扰［11～13］等。

5 结语

维纳滤波器适用于输入特性已知且广义平稳的随机过程，使用全部的过去观测值完成这一“去相关”过程；卡尔曼滤波器还可适用于非平稳随机过程，特别适合对模型已知系统的实时预测，当应用于噪声较大系统时，预测结果将十分依赖观察值；LMS自适应滤波器更适合于对非平稳随机过程中变化的信号进行滤波，取得的结果明显优于维纳滤波器，其波形与维纳滤波器相比更平滑、更接近目标信号。