基于变分模态分解算法的隧道爆破振动信号光滑降噪模型

彭亚雄，刘广进，苏 莹，刘运思，张 超

(1.湖南科技大学 岩土工程稳定控制与健康监测湖南省重点实验室，湖南 湘潭 411201；2.湖南科技大学 土木工程学院，湖南 湘潭 411201)

爆破是一种有效的岩体开挖方法，在隧道工程中广泛使用。炸药爆炸产生的地震波会引起隧道围岩及结构振动，对隧道稳定性及邻近建(构)筑物造成不利影响[1]。准确分析爆破振动特征及衰减规律是有效控制爆破振动有害效应的基础。由于复杂的工程环境、电磁干扰和监测仪器误差等因素的影响，实测爆破振动信号中包含大量高频噪声，导致信号失真。为了准确分析隧道爆破振动特性，必须对实测信号进行降噪处理。

信号降噪过程包括信号分解和去噪两个部分，目前最常用的信号分解方法有小波类(小波[2]、小波包[3]、平移不变小波[4])和经验模态分解类(经验模态分解(empirical mode decomposition，EMD)[5]、集合经验模态分解(ensemble empirical mode decomposition，EEMD)[6]、互补集合经验模态分解(complementary ensemble empirical mode decomposition, CEEMD)[7]。为了获得更好的降噪效果，还可以与独立成分分析[8]和排列熵[9]等优化算法结合，这些方法已经在爆破振动信号降噪处理中得到了较好地应用。小波类降噪方法是基于小波变换算法，具有良好的时频局部化特性，但在降噪过程中小波基函数和分解层次难以确定[10]，使得这类方法的自适应性不强，降噪效果难以保证。EMD是一种具有较好自适应能力的信号分解方法，对爆破振动信号分解有较好的适应性，但存在端点效应和模态混叠问题。EEMD和CEEMD改进算法的提出在一定程度上解决了EMD算法的这两类问题，信号降噪效果有所提高[11]，但其基本的分解模式并未得到根本的改变。

信号分解后的去噪方法包括强制降噪和阈值降噪。强制降噪是将具有高频特征的信号分量认定为噪声分量，直接去除后进行信号重构[12]。该方法降噪效果较好，但对分解算法精度要求高且人为因素影响较大。阈值降噪是对高频分量进行阈值处理，将信号有效成分进行重构，去除无效的噪声成分[13]。采用硬阈值方法会使得重构信号产生振荡；而软阈值方法的信号连续性较好，但其影响了重构精度[14]。

变分模态分解(variational mode decomposition，VMD)是由Dragomiretskiy等[15]提出了一种非递归的信号自适应分解方法，利用迭代搜寻变分模型的最优解，确定各分解部分的频率中心及带宽，能够自适应地进行信号频域划分和分量分离。该方法克服了EMD递归分解产生的端点效应和模态混叠问题，具有较好的鲁棒性。本文对爆破振动信号进行VMD分解，以分解得到的本征模态函数(intrinsic mode function，IMF)建立低通滤波算法；根据滤波算法重构误差和光滑程度获得最优光滑降噪模型，并应用于实测隧道爆破振动信号降噪处理。

1 VMD算法

VMD算法将模态估计转变为变分问题，通过迭代寻找频率范围内的变分模态最优解，不断更新各模态函数及中心频率，得到若干具有一定带宽的IMF。VMD算法将原始信号x(t)分解为K个中心频率为ωk的模态函数uk，其中K为预设模态分量个数[16]。定义模态函数为调幅-调频信号，即

uk(t)=Ak(t)cos(φk(t))

(1)

式中：uk(t)为第k个模态分量；Ak(t)和φk(t)分别为瞬时幅值和相位。

为了得到某带宽的IMF，①对uk(t)进行希尔伯特变换，得到解析信号和单边频谱ψ；②对解析信号加入估计中心频率，并将各模态频谱转换至基频带；③计算解析信号梯度的平方L2范数，估计各模态信号带宽，得到约束性变分问题

(2)

式中：{uk}为信号分解得到的K个模态分量；{ωk}为各分量对应的中心频率；δ(t)为脉冲函数。

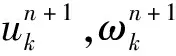
(3)

(4)

(5)

将原始含噪信号进行VMD分解后得到K个IMF分量，I1～IK的主频逐渐增加，而噪声成分主要存在于高频部分，因此从原始信号x(t)中由高频向低频逐步除去累积的IMF分量，即构建低通滤波算法，获得多个低通信号，通过对比分析各低通信号特征，获得最优降噪信号，达到去除噪声的目的。

2 信号光滑降噪模型

2.1 滤波算法重构误差

对原始信号x(t)进行VMD分解，以分解得到的IMF建立低通滤波算法，如式(6)所示

(6)

滤波算法的重构误差采用降噪后信号与原始信号的均方根误差ef表示，如式(7)所示。

(7)

2.2 滤波算法光滑程度

在其定义域内各点均具有一阶连续导数的曲线为光滑曲线。光滑曲线上任一点的左导数和右导数存在且相等；对于两条以上曲线构成的光滑曲线，两条曲线交点处的导数存在且相等[17]。

因此，设曲线u(x)和v(x)相交于x0，且在该点连续可导，则有

(8)

若两条曲线在x0处光滑，则应该满足u(x)和v(x)在x0点的曲率相等，即

Ku|x=x0=Kv|x=x0

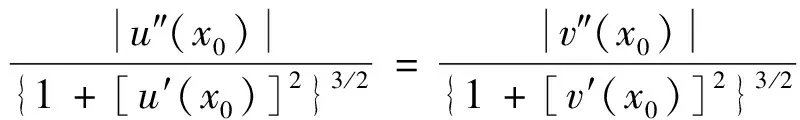
(9)

将式(8)代入式(9)，可得

u″(x0)=v″(x0)

(10)

根据导数的定义，u″(x)和v″(x)可以表示为

(11)

(12)

将式(9)和式(11)、式(12)代入式(10)，可得

v(x0+2h)-u(x0-2h)-2[u(x0-h)-u(x0-h)]=0

(13)

曲线u(x)和v(x)组成的f(x)在x0点处的光滑度可表示为

SN|x=x0=f(x0+2h)-f(x0-2h)-2[f(x0-h)-f(x0-h)]

(14)

式中，h为采样间隔。曲线的SN值越小，说明曲线越光滑。

将曲线SN的均方根误差定义为滤波算法的平整度，记为eS。该值反映了降噪后信号的光滑程度，计算时应注意去掉采样样本中两个端点。

2.3 目标函数

对原始信号进行VMD分解得到IMF，建立低通滤波算法。考虑滤波算法的重构误差和光滑程度，设置了一个权重系数μ，得到光滑降噪模型的目标函数

F=μ·ef+(1-μ)·eS

(15)

权重系数μ通常为0.3[18]。计算得到目标函数F值最小为最优解，最优解对应于最优滤波算法模型，其降噪效果最好。

2.4 降噪效果评价指标

信号在分解过程中会导致部分成分丢失，将原始信号与降噪后信号的标准差SD(standard deviation)作为评价处理信号失真情况的评价指标。并采用信噪比ξ、降噪后和原始信号的均方根误差ef作为评价指标[19]，分析隧道爆破振速信号降噪效果。均方根误差ef如式(7)所示，重构标准差r和信噪比ξ定义如下：

(1)重构标准差r

(16)

(2)信噪比ξ

(17)

ESD用于评估信号保真度，其值越小说明在分解过程中信号成分丢失越少。信噪比ξ反映原始信号和噪声的能量关系，信噪比ξ越大表明降噪后信号更好的保留了原始信号特征。ef反映了噪声的平均能量值，也体现了降噪后与原始信号的相似程度，通常其值越小效果越好。此外，除了采用定量参数客观评价降噪效果，还应该分析降噪前后信号波形特征，确保特征波形的一致性和明显噪点已去除干净。

3 工程应用

3.1 实测信号降噪

以山东省烟台市某地下水封石洞液化石油气储库工程为依托工程，工程包括不同高程、不同位置的三种储气库：LPG库、丙烷库与丁烷库，均采用光面爆破开挖。现场采用TC-4850型测振仪进行测试。选取丙烷库洞室爆破开挖的一条实测典型振动信号为研究对象，如图1所示。该实测信号的采样频率为3 200 Hz，根据Nyquist采样定理，实测信号频率为1 600 Hz；采用时间为1 s，共采集3 200个采样点。

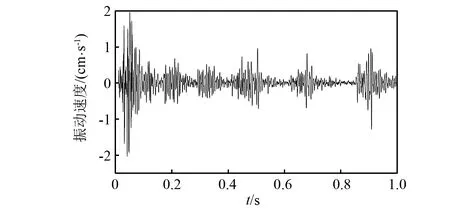
图1 实测爆破振动信号(s1)

使用VMD算法进行信号分解，需要预先设定的参数包括：模态分量个数K、惩罚因子α、保真度τ和收敛条件ε。保真度τ和收敛条件ε通常采用默认值[20]。经反复试算，惩罚参数确定为α=4 800，以保证分解过程的细节特征保留度。对于模态分量个数K，分别取K=2, 3, 4, …, 9对实测信号进行分解，各IMF的中心频率如表1所示。当某K值分解的各IMF分量主频保持相对稳定；而以K+1值分解，仅最后一个IMF分量主频增大，认为K值最佳。由表1可知，K=8分解的各IMF分量主频保持相对稳定；而K=9时，最后一个IMF分量主频增加，因此该信号的本征模态函数的分量个数K设定为8，得到信号VMD分解的IMF分量如图2所示。

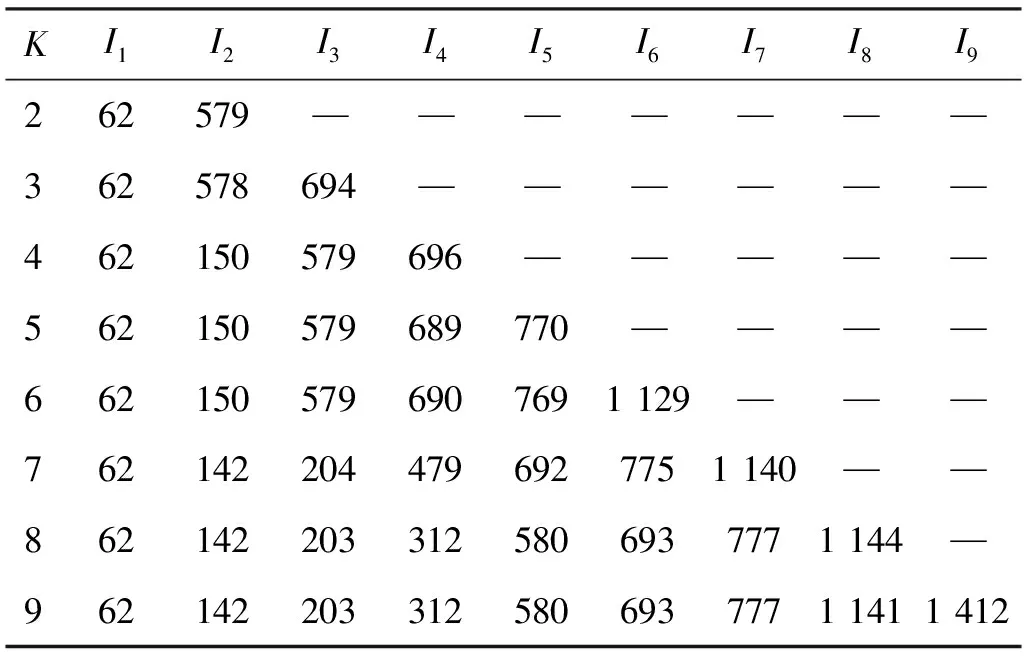
表1 不同K值分解的IMF分量主频

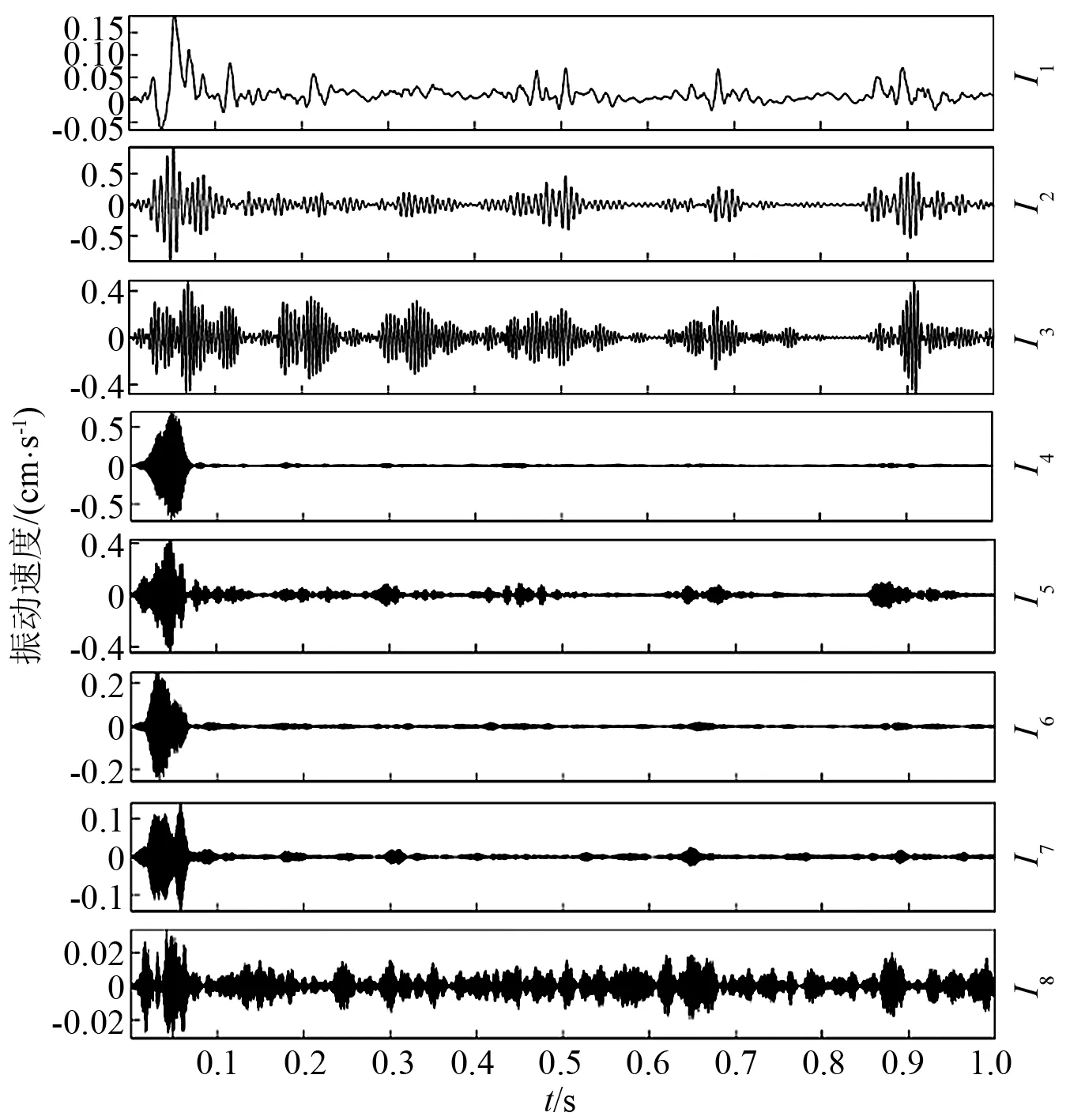
图2 振动信号 VMD分解结果

由表1和图2可知，采用VMD算法对实测信号进行分解共得到8个IMF分量，I1～I8主频逐渐增加。构建低通滤波模型，如式(18)所示。分别计算各滤波模型的平整度、重构标准差和目标函数F值，各指标的结果如图3所示。

(18)

由图3可知，降噪后信号D1～D8的ef逐渐降低，而eS逐渐增加，说明降噪后信号与原信号的相似程度增加而光滑程度降低。D5的目标函数F值最低，其降噪效果最佳。比较目标函数F值，D4和D5的F值差异不大。因此，给出原始信号与去噪信号(D4和D5)的对比图，如图4所示。

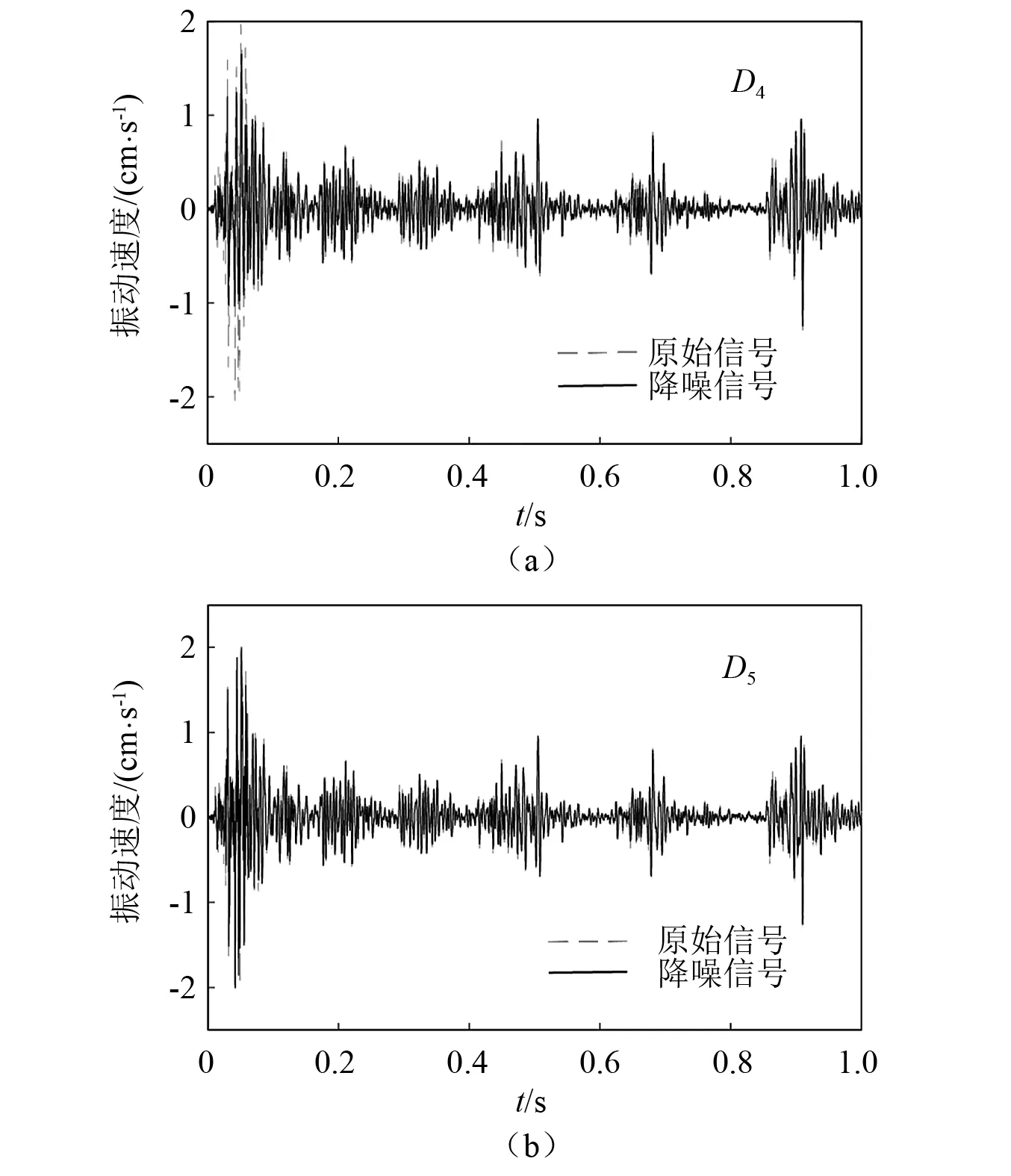
图4 原始信号与降噪后信号对比

由图4可知，尽管D4与D5的目标函数F值相差不大，D5信号的降噪效果明显更好。其在振动速度峰值处与原始信号相似度更高，D4存在明显的降噪过度。

3.2 时频能量分析

AOK时频分析技术能较好地反映爆破振动信号的时频特性[21]。为了进一步验证VMD光滑降噪模型的效果，利用AOK时频分析方法对原始信号和降噪后信号的时频能量进行对比。信号的时频能谱如图5所示。图5中：X为时频能量峰值；Y为主频。

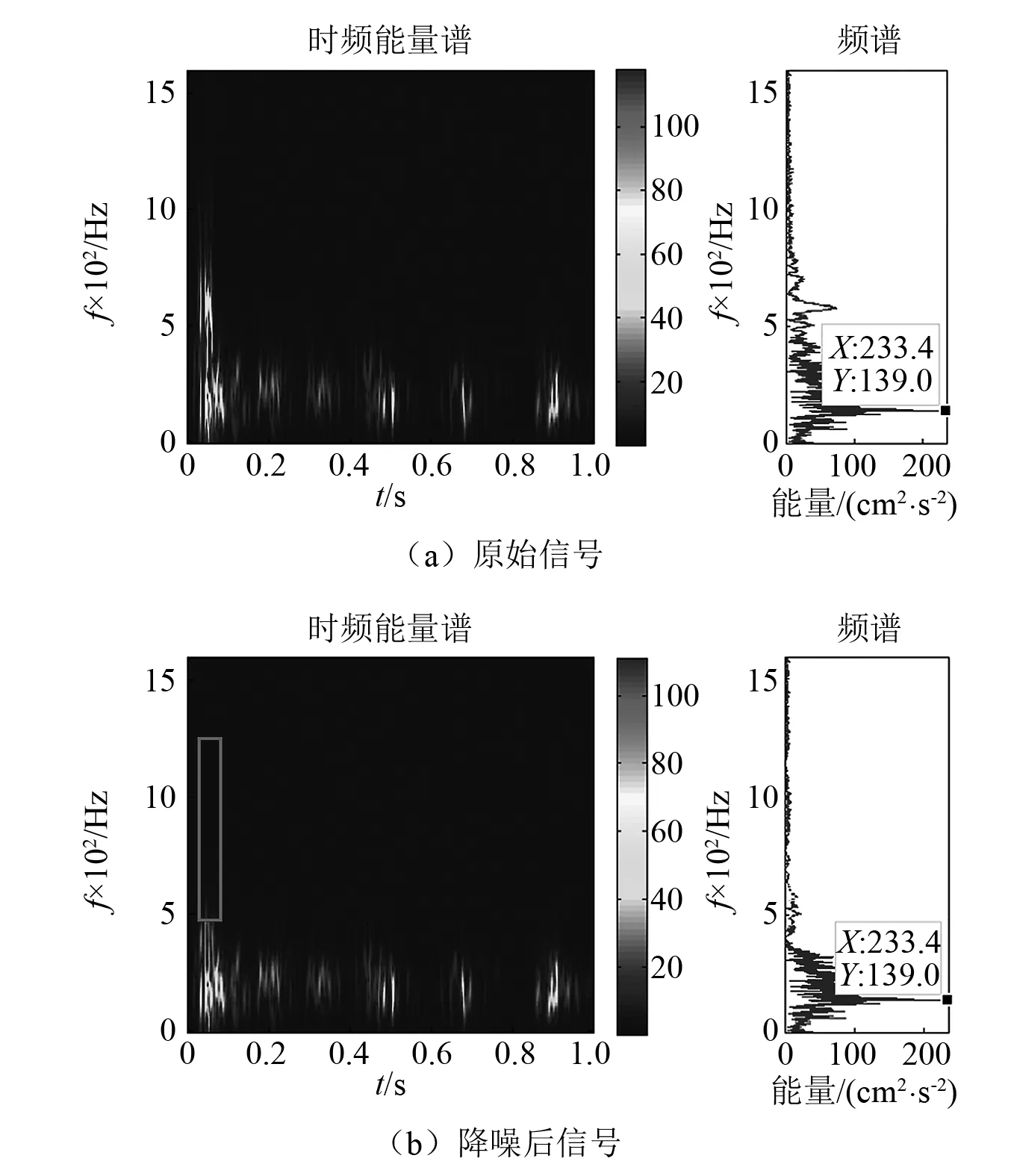
图5 原始信号与降噪后信号时频能量谱

由图5可知，信号时频能量主要分布在0～300 Hz的频率范围和0～1 s的时间范围内。原始信号在频率500 Hz以上范围存在明显的噪声成分，是造成原始信号失真的主要原因(见图5(b)中方框)，利用VMD光滑降噪模型较好地去除了这些噪声成分；且在0～300 Hz内，低频能量分量没有明显降低。原始信号与降噪后信号的主频均为139 Hz，时频能量峰值均为233.4 cm2/s2。表明VMD最优光滑降噪模型不仅能成功地去除高频噪声能量，而且对低频信号能量影响较小。

4 降噪效果对比分析

基于EMD、CEEMD算法同样可以构造相应的光滑降噪模型。采用EMD、CEEMD和VMD光滑降噪模型对3组隧道爆破振动信号进行降噪处理，原始信号与降噪后信号如图6所示。计算原始信号与重构信号的标准差ESD、信噪比ξ、降噪后信号和原始信号的均方根误差ε，如表2所示。

表2 爆破振动信号降噪效果指标

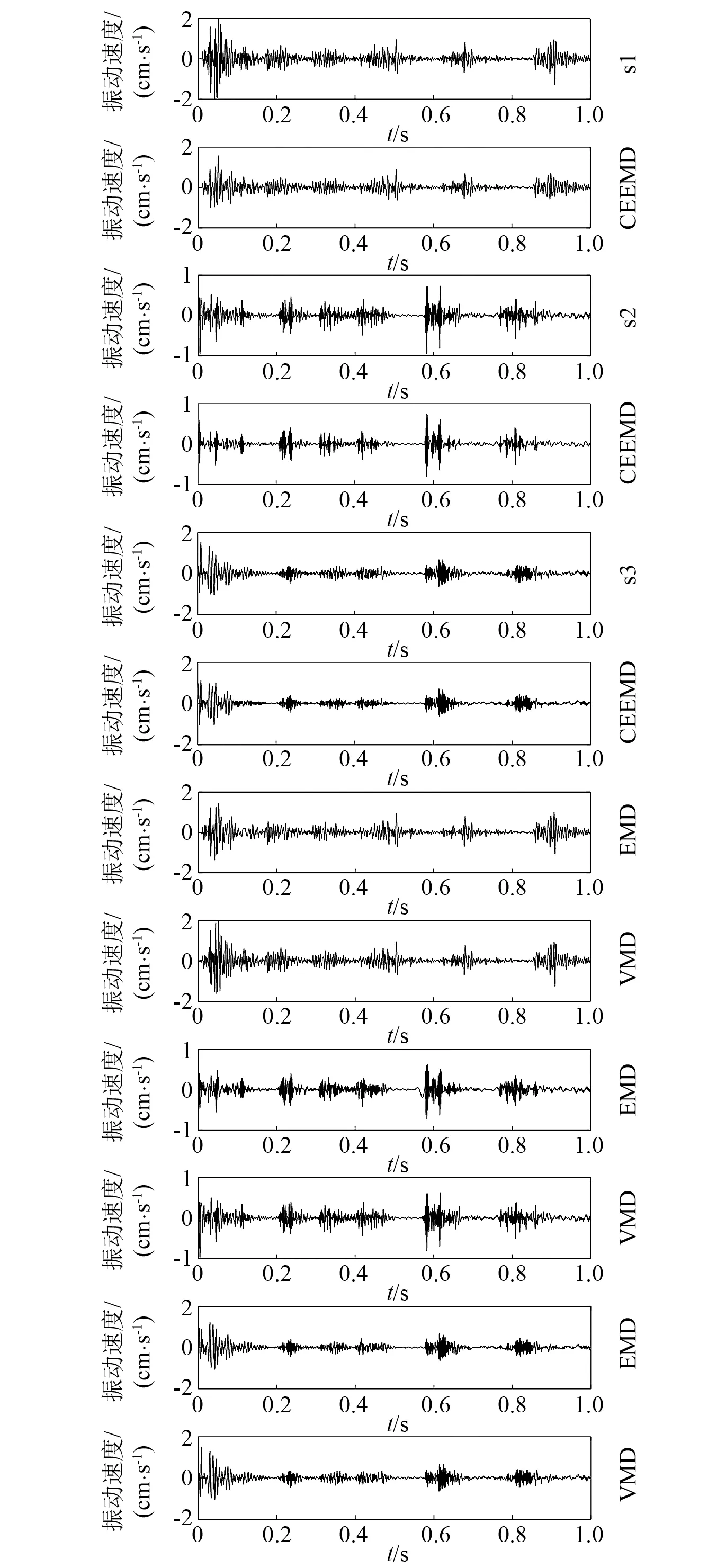
图6 原始信号与降噪后信号对比(EMD，CEEMD，VMD)

由图6和表2可知，采用EMD，CEEMD和VMD光滑降噪模型对三组实测隧道爆破振动信号进行了降噪，均取得一定程度降噪效果，去除了部分高频噪声。3组实测信号分解与重构过程中，原始信号与重构信号的标准差ESD在0.011 1～0.023 4，说明三种模型均具有较好的保真性。其中EMD模型的重构标准差ESD均最大，而最小值则存在差异，说明EMD，CEEMD和VMD模型在处理不同实测信号时其保真性存在差异。对比三种光滑降噪模型的降噪效果评价指标，在3组实测信号降噪中VMD模型的降噪后信号信噪比ξ均最大，CEEMD模型略大于EMD模型；VMD模型的均方根误差ε均最低，CEEMD模型略低于EMD模型。VMD光滑降噪模型相比于其他两种模型，能够更好的去除高频噪声信号，且降噪后信号的波形更接近原始信号。因此，基于VMD算法的光滑降噪模型在振动信号降噪方面具有一定的优越性，且能够更好地保留隧道爆破振动信号中的有效信息。

此外，CEEMD作为基于EMD的改进算法，具有较好的信号分解效果，并在一定程度上克服了模态混叠现象，CEEMD光滑降噪模型的降噪效果优于EMD模型。

5 结 论

隧道爆破振动信号中存在较多高频噪声，导致实测振动信号中所包含的信息常被噪声信号所掩盖。针对这一问题提出了基于VMD算法的光滑降噪模型，用于隧道爆破振动信号降噪处理。

(1)利用VMD算法对隧道爆破振动信号进行分解，得到不同频带的IMF分量，进而构建低通滤波算法。考虑滤波算法的重构误差和光滑程度构造目标函数，计算目标函数的最优值得到最优降噪信号。工程应用表明该方法达到较好地去除高频噪声的目的。

(2)利用AOK时频分析技术，对比分析降噪前后振动信号的时频能量谱，VMD最优光滑降噪模型不仅能成功地去除500 Hz以上的高频噪声能量，而且对低频信号能量影响较小。

(3)将EMD，CEEMD和VMD光滑降噪模型进行对比分析，三种方法都具有较好的保真性和降噪效果，其中VMD模型的降噪效果指标均优于EMD，CEEMD模型，验证了基于VMD算法的光滑降噪模型的有效性，对隧道爆破振动信号降噪及分析具有指导意义。