铺缆船用电缆埋设犁土壤挖掘阻力计算

吴占阳， 王 赟， 许素蕾， 汤维佳

(上海振华重工(集团)股份有限公司，上海 200125)

0 引 言

海底电缆埋设犁是海洋铺缆船用关键设备，可实现对海底电缆的边挖沟边埋设工作。挖掘阻力是埋设犁在挖沟埋缆作业过程中所受主要载荷，主要来自埋设犁犁刀正面土壤的挖掘反力和侧面土壤的摩擦力。目前针对土壤挖掘阻力的计算，可根据库仑土压力理论计算犁刀正面挖掘反力，但对于犁刀侧面的土壤摩擦力，主要基于经验公式方法[1]；也可在库仑土压力理论基础上采用修正系数的方法[2]。这些计算方法，对于既定犁刀尺寸和结构，如果试验数据丰富，则获得的结果相对准确，但如果试验数据缺乏，且犁刀结构和尺寸有较大变化时，计算结果则会出现较大偏差。根据土力学基本原理，通过对某型埋设犁犁刀正面挖掘反力和侧面摩擦力的计算，在不依赖试验数据的情况下，介绍一种计算埋设犁土壤挖掘阻力的理论方法。

1 埋设犁正面土壤阻力计算

埋设犁在海底切削土壤时，其正面在拖曳力作用下切削土壤，根据土力学理论，这时土壤受到被动土压力。当压力达到一定程度时，对应破坏面上的剪应力超过土壤抗剪切应力，土壤在破坏面发生滑动。按照库仑土抗剪切强度理论：

τf=c+σtanφ

(1)

式中:τf为土的抗剪切强度，kPa；c为土的内聚力，kPa，取50 kPa(重黏土)；σ为剪切面的法向应力，kPa；φ为土的内摩擦角，(°)。

图1为来自土壤中某一点的单元体的受力状态示例。图1 中：σ1和σ3为主应力，且定义σ1>σ3；mn为单元体上任意剪切面；α为单元体剪切面mn与小主应力σ3方向的夹角；ds为微单元体剪切面mn的面积；τ为剪切面mn上的剪应力。

图1 土壤单元体受力示例

结合材料力学二应力理论，可得：

(2)

根据式(1)和式(2)，可得：

(3)

当土体中任意一点在某一平面上的剪应力等于土的抗剪切强度时，这种状态被称为极限平衡状态。根据相关土力学原理，当土体发生剪切破坏时，其破坏面不是发生在剪切强度最大的面上，而是发生在与最大主应力作用面成45°+φ/2的面上[3]。此时，单元体平面mn与小主应力σ3方向的夹角被称为破裂角，标记为αf，且αf=45°+φ/2。将αf代入式(3)，可得：

(4)

根据黏性土极限平衡条件[4]，在极限平衡状态下：

(5)

同时，当土壤处于极限平衡状态时，满足：

τf=τ

(6)

埋设犁在海底切削土壤时，一般取φ=40°，c=50 kPa，则土壤破坏面的破坏角αf=45°+φ/2=45°+40°/2=65°。

将上述已知数据代入式(1)和式(4)～式(6)，得到结果如表1所示。

表1 土壤应力计算结果 kPa

图2～图5为某型埋设犁犁刀不同受力模型示例。图4和图5以犁沟顶面和斜型犁刀正面交点为坐标原点O，水平向右为横坐标正向，竖直向下为纵坐标正向，建立一个平面坐标系，以便进行后续力学位置计算和力的合成。

图2 某型埋设犁正面土壤阻力分析示例

图3 某型埋设犁正面土壤阻力计算示例

图4 某型埋设犁正面土壤阻力分解示例

图5 某型埋设犁侧面土壤摩擦力分析示例

根据经典土力学理论，当埋设犁前进挖沟时，犁刀前面的土壤可以视为一面竖直的挡土墙(见图2)。由图2可看到：当埋设犁前进挖沟时，按犁刀受力最大工况，可假定σ1的作用方向垂直于下部犁刀和犁刀正面，下部犁刀和犁刀正面会受到来自土壤的阻力。图3为某型埋设犁正面土壤阻力计算示例。在图2和图3中，某型埋设犁挖沟最大深度H为3 200 mm，其中下部犁刀挖沟深度H1为470 mm，斜型犁刀正面挖沟深度H2为 2 730 mm。

如图3所示，当埋设犁前进挖沟至深度3 200 mm时，下部犁刀和斜型犁刀正面分别受到来自土壤的正压力Fn1和Fn2：

(7)

(8)

式(7)和式(8)中：S1为下部犁刀面积，m2；S2为斜型犁刀正面面积，m2；b为犁刀宽度，m；L1为下部犁刀长度，m；L2为斜型犁刀正面长度，m。

图4为某型埋设犁正面土壤阻力分解示例。将上述计算结果Fn1和Fn2进行水平和垂直各方向的分解。Fn1分解为：水平力Fx1，垂直力Fy1，kN；Fn2分解为：水平力Fx2，垂直力Fy2，kN。上述水平和竖直方向力的方向定义为：竖直向上为正；水平向右为正(与犁的前进方向相反)。可得：

Fx1=Fn1cosθ1

(9)

Fy1=-Fn1sinθ1

(10)

Fx2=Fn2cosθ2

(11)

Fy2=Fn2sinθ2

(12)

联立式(7)～式(12)，计算结果如表2所示。

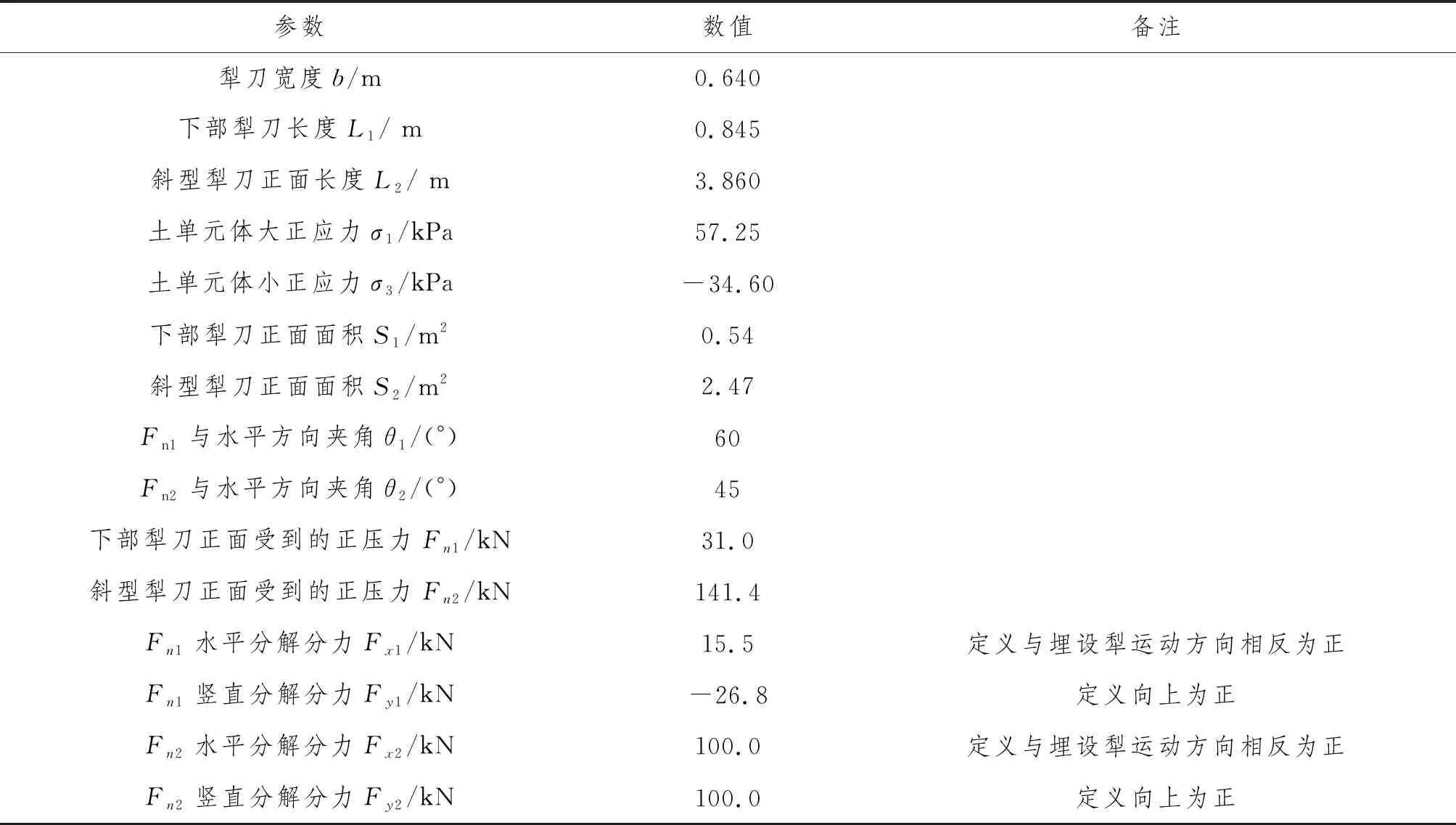
表2 某型埋设犁正面土壤阻力计算结果

2 埋设犁侧面土壤摩擦力计算

埋设犁在作业过程中，其犁体两侧面受到来自土壤的正压力和摩擦力，其受力部分如图5所示。根据犁体侧面与海底土壤接触情况，将犁体侧面划分成3个部分：三角形OAB，长方形ACDE，梯形EDGF。

根据图5，埋设犁上端面OAE直线的解析方程为

YOAE=0

(13)

埋设犁下端面即斜型面OB直线的解析方程为

YOB=X

(14)

埋设犁底面CDG直线的解析方程为

YCDG=3.2

(15)

埋设犁上部斜型面EF直线的解析方程为

(16)

下文分别求犁体的三角形OAB、长方形ACDE、梯形EDGF区域内犁体侧面正压力和摩擦力，在计算中钢与土壤的摩擦因数μ为0.5。

埋设犁在水下作业时，其侧面受到来自土壤的侧面压力和由此产生的摩擦阻力。埋设犁的两侧面属于垂直面(非倾斜面)，当埋设犁作业前进时，两侧土壤会对其产生侧压力，将这种土侧压力看作是静止土侧压力。根据相关土力学原理，可用静止土压力理论进行计算。

根据静止土力学理论，设静止土压力强度为σ0(见图6)，则

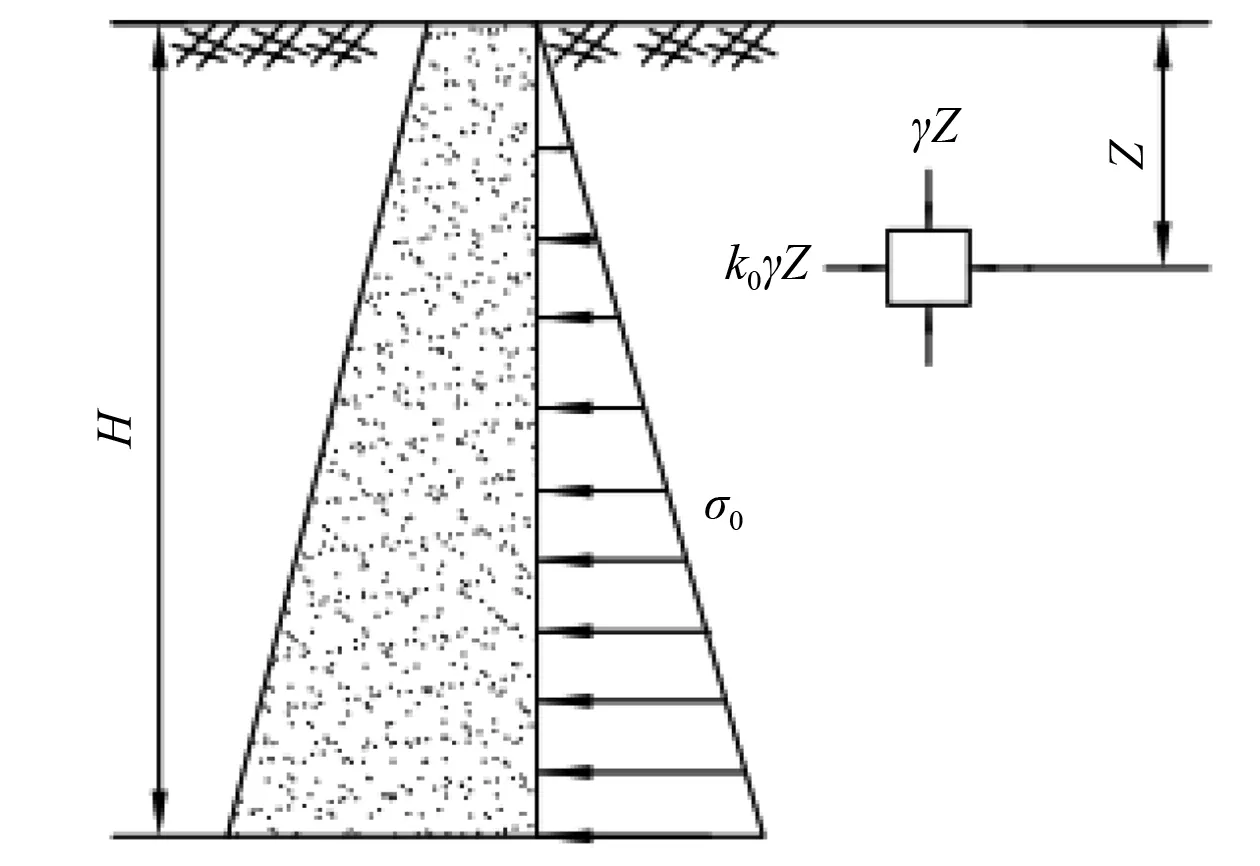
图6 静止土压力计算示例

σ0=γZK0

(17)

式中：γ为海底土壤的容重，一般取16.5 kN/m3；Z为作用位置深度，m；K0为静止土压力因数，通常对于黏性土，K0取0.5～0.7，非黏性土取0.35～0.50，此处按黏性土取K0=0.7。

2.1 三角形OAB区域土壤正压力和摩擦力计算

三角形OAB区域，结合式(14)和式(17)，单位宽度土墙对埋设犁侧面的侧压力计为

(18)

运用定积分的元素法原理[5]，在三角形OAB区域内得到的侧面正压力为

(19)

式中：XB=2.727 m，XO=0 m，XB、XO分别表示点B、点O在X轴的坐标。经计算得到NOAB=39 kN。

相应地，三角形OAB区域内受到的局部摩擦阻力大小为(含正反2个侧面)fOAB=2μNOAB=39 kN。

2.2 长方形ACDE区域土壤正压力和摩擦力计算

长方形ACDE区域，结合式(13)、式(15)和式(17)，单位宽度土墙对埋设犁侧压力为常数：

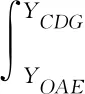
(20)

则在长方形ACDE区域内得到的侧面正压力为

(21)

式中：XC=2.727 m，XD=3.818 m，XC、XD分别表示点C、点D在X轴的坐标。经计算得到NACDE=64 kN。

相应地，长方形ACDE区域内受到的局部摩擦阻力大小为(含正反2个侧面)fACDE=2μNACDE=64 kN。

2.3 梯形EDGF区域土壤正压力和摩擦力计算

梯形EDGF区域，结合式(15)、式(16)和式(17)，单位宽度土墙对埋设犁侧压力为

31.07+14.67X-1.93X2

(22)

则在梯形EDGF区域内得到的侧面正压力为

(23)

式中：XD=3.818 m，XG=8.027 m，XG为点G在X轴的坐标。经计算得到NEDGF=199 kN。

相应地，梯形EDGF范围内受到的局部摩擦阻力大小为(含正反2个侧面)fEDGF=2μNEDGF= 199 kN。

2.4 侧面摩擦力作用点位置

在静止土压力强度σ0的作用(见图7)下，对单位长度挡土墙侧面压力沿深度方向逐渐加大分布。这种分布作用可以等效成一个集中力，该力大小为E0，作用在某一深度位置Z′。

图7 作用位置求解示例

假设E0作用位置深度为Z′，则单位长度的挡土墙在任意作用位置深度Z处，对深度Z′处的力

矩满足如下关系：

(24)

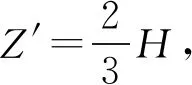
图8为某型埋设犁侧面土壤摩擦力合成示例。在图8中，以犁沟顶面和斜型犁刀正面交点为坐标原点O，水平向右为横坐标正向，竖直向下为纵坐标正向，建立一个平面坐标系。在埋设犁犁刀侧面三角形OAB区域，沿着犁刀侧面X方向，单位长度挡土墙集中力E0=EOAB沿直线OH分布其上，根据单位长度挡土墙集中力E0作用位置在距沟底1/3深度处的结论，直线OH的方程为

(25)

由式(18)可知：EOAB是关于X的函数。因此，侧面正压力也可以等效到OH上某一点。假设该点深度位置为y′,对应该点横坐标为X′，则根据力矩平衡关系，可得：

(26)

将式(18)、式(25)代入式(26)，且XO=0 m，XH=2.727 m，XH为点H在X轴的坐标。经计算得到y′=1.364 m 。

在图8的埋设犁侧面矩形ACDE区域内，沿犁刀侧面X方向，单位长度挡土墙集中力E0=EACDE沿直线IJ分布其上，根据单位长度挡土墙集中力E0作用位置在距沟底1/3深度处的结论，直线IJ为一条水平直线，方程为

图8 某型埋设犁侧面土壤摩擦力合成示例

(27)

由式(20)可知：EACDE为常数。因此，侧面正压力也可以等效到IJ上某一点。假设该点深度位置为y″,则容易得到y″=2.133 m。

在图8的埋设犁侧面梯形EDGF区域内，沿犁刀侧面X方向，单位长度挡土墙集中力E0=EEDGF沿直线JK分布其上，根据单位长度挡土墙集中力E0作用位置在距沟底1/3深度处的结论，直线JK为一条直线，方程为

y=0.192x+1.398

(28)

由式(22)可知：EEDGF是关于X的函数。因此，侧面正压力也可以等效到JK上某一点。假设该点深度位置为y‴，则根据力矩平衡关系，可得：

(29)

将式(22)和式(28)代入式(29)，且已知XJ=3.818 m，XK=8.027 m，XJ、XK分别表示点J、点K在X轴的坐标。经计算得到y‴=2.341 m。

根据上述计算结果，在埋设犁犁刀侧面正压力作用位置确定后，对应其所产生的摩擦力集中作用点位置相应确定。这3个区域范围的摩擦力fOAB、fACDE、fEDGF的作用位置如图8中y′、y″和y‴所示。由于这3个摩擦力为水平方向，水平坐标位置与力产生的转矩无影响，此处水平坐标位置不作具体计算。

3 埋设犁犁体挖掘阻力合成计算

3.1 挖掘阻力合力计算

上文经过计算，已获得埋设犁在进行作业时犁刀体受到来自土壤的各种阻力，包括：埋设犁正面所受土壤阻力的水平分力Fx1、Fx2；正面土壤阻力竖直分力Fy1、Fy2；侧面压力NOAB、NACDE、NEDGF；侧面摩擦力fOAB、fACDE、fEDGF。其中，犁刀体两个侧面压力大小相等，方向相反。在计算整个埋设犁的平面力系时由于相互抵消，可以不考虑。

综上所述，某型埋设犁犁刀体受到的挖掘阻力如表3所示。

由表3可知：某型埋设犁在挖沟到最大深度时，受到来自土壤的阻力，可按水平和竖直两个方向进行大小合成，则有水平合力Fx(与埋设犁运动方向相反为正)和竖直合力Fy(向上方向为正)分别为

表3 某型埋设犁挖掘阻力

Fx=Fx1+Fx2+fOAB+fACDE+fEDGF=417.5 kN

(30)

Fy=Fy1+Fy2=73.2 kN

(31)

3.2 挖掘阻力合成

现假设上述2个力合成至埋设犁的某一点处，相对于坐标原点而言，设该合成力的坐标为(X,Y)，上述分析的Fx1、Fy1、Fx2、Fy2、fOAB、fACDE、fEDGF各力的作用点坐标如图9所示。在图9中，以犁沟顶面和斜型犁刀正面交点为坐标原点O，水平向右为横坐标正向，竖直向下为纵坐标正向，建立一个平面坐标系。各水平方向作用力绕原点O形成的力矩之和可以用总的水平力Fx与其纵轴坐标Y的乘积等效；竖直方向作用力绕原点O形成的力矩之和可以用总的竖直力Fy与其横轴坐标X的乘积等效。相关方程为

图9 某型埋设犁挖掘阻力合成示例

(32)

将各已知数据代入式(32)可得到X=1 718 mm；Y=2 119 mm。

最终埋设犁挖掘阻力合成力位置及大小如表4所示。

表4 某型埋设犁挖掘阻力合成

4 结 论

根据土壤力学的基本原理，在电缆埋设犁挖掘海底土壤过程中，运用库仑抗剪切强度理论，对某型埋设犁正面挖掘反力进行理论分析与计算；运用静止土理论，对埋设犁挖掘过程中犁刀侧面受到的摩擦力进行理论分析与计算；并运用力学平衡原理，对埋设犁受到的正面挖掘反力和侧面土壤摩擦力进行大小和位置的等效合成。在缺乏有效试验数据的情况下，为埋设犁海底挖掘阻力的分析与计算提供一种通用性的理论方法，突破经验公式的局限性，并为埋设犁犁刀的设计及整机力学分析提供一种理论指导。然而，作为一种理论计算方法，在实际运用时需要繁琐的数学建模和大量图例，因此相对于经验公式，计算工作量增加。