基于改进遗传算法的拣货机器人手臂运动误差自动校正方法

刘 媛

(安徽电子信息职业技术学院 机电工程学院,安徽 蚌埠 233000)

拣货机器人在作业过程中运行轨迹的控制中由于多种因素的影响,导致其拣货过程中手臂出现一定误差,影响正常作业效率[1].为此,相关研究者对降低机器人手臂运动误差进行了很多研究.

当前,对机器人手臂运动误差校正方法主要包括模糊参数辨识法、空间参数融合方法,特征分布式检测方法等.这些方法中通过构建自主作业型拣货机器人手臂参数控制模型,结合对自主作业型拣货机器人手臂的动作特征识别进行姿态参数估计[2-3],计算自主作业型拣货机器人手臂的运动位姿的特征统计量等,在一定程度上降低了拣货机器人手臂运动误差,但当前方法对机器人拣货中手臂误差校正的准确性不高,仍需要进一步的改进.

对此,本文提出基于改进遗传算法的拣货机器人手臂运动误差自动校正方法.构建机器人拣货机器人手臂运动参数分布模型,获取其运动过程中的相关参数;通过RBF 神经网络对其自适应区域参数进行控制,采用改进遗传算法和姿态参数融合方法完成其误差的校正.与传统校正方法相比本文方法可有效提升拣货机器人手臂运动的校正精度,且其自适应性能较好,具有一定优势.

1 运动误差信息融合

1.1 拣货机器人手臂运动学模型

为了实现基于改进遗传算法的自主作业型拣货机器人手臂位姿误差自动校正,首先构建自主作业型拣货机器人的运动学分析模型,结合对自主作业型拣货机器人的运动特征分辨提取结果,采用双目视觉跟踪融合,实现对自主作业型拣货机器人的机器视觉参数识别,结合对自主作业型拣货机器人的动态特征点匹配结果[4-5],建立自主作业型拣货机器人的惯性融合参数模型,提高自主作业型拣货机器人的运动控制能力和误差校正能力.自主作业型拣货机器人的运动控制流程如图1 所示.

图1 自主作业型拣货机器人的运动控制流程

根据图1运动流程控制,初始化得到全局自主作业型拣货机器人手臂姿态,根据姿态参数估计,进行拣货机器人手臂运动双目视觉分析,在自主作业型拣货机器人的位姿确定下[6],若矩阵C满足C=C1(xtg+i)2,其中i=1,2,…,n,xtg代表求共轭,引入自主作业型拣货机器人手臂运动误差反馈调节[7],得到自主作业型拣货机器人的手臂运动位姿分布特征量,即kb=2πi,在目标位姿分布中,自主作业型拣货机器人的位姿状态特征量为cr≥1,那么,对自主作业型拣货机器人的结构参数优化得到

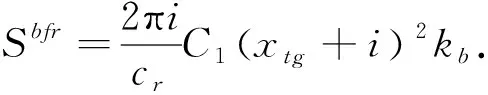
(1)

结合空间模糊度特征寻找最优解,得到全局自主作业型拣货机器人手臂姿态信息[8],在仿射区域α中,拣货机器人手臂运动学模型为

(2)

将传感器放置自主作业型拣货机器人的运动学参数采集模块中,采用模糊度控制技术,得到自主作业型拣货机器人手臂优化参数k(gc)为

(3)

UH=T(uhry+uhby).

(4)

令T∈{1,2,3,…,n},综上分析,构建自主作业型拣货机器人手臂参数运动学模型.

1.2 自主作业型拣货机器人手臂运动误差信息融合

根据上述构建的拣货机器人手臂运动学模型,将其运动过程中的运动误差信息进行融合.在此过程中,构建拣货机器人手臂运动参数分布模型,根据手臂空间姿态参数采集拣货机器人手臂运动信息,构建辨识参数控制模型,完成其运动过程中运动误差信息的融合.

设置自主作业型拣货机器人运动状态函数为

(5)

考虑拣货机器人手臂运动控制系统刚体特征,将静点β加入其手臂运动位姿计算,得到自主作业型拣货机器人的手臂运动误差自动校正的线性化处理模型为

(6)

其中,Clrf、Cjrf分别为自主作业型拣货机器人手臂运动误差自动校正的稳定性平衡点.将所有点增加到手臂运行路线中,得到机器人手臂运动的误差融合结果

(7)

根据上述机器人手臂运动的误差融合结果,对自主作业型拣货机器人的模糊参数进行辨识,得到机器人手臂运动状态未知点、动点的辨识函数为:

Drsgt=dx1(kx+g)(sin-1α+cos-1β),

(8)

(9)

2 运动误差自动校正

2.1 拣货机器人手臂运动参数的遗传进化算法

假设遗传算法中种群规模描述为z,种群集合表示为zq={zq1,zq2,…,zqn,},其中,zqn表示种群中数据的第n个个体数据,此时种群中的平均个体数据为

(10)

(11)

可以看出,该算法的种群方差可表示为l维行向量,若l维该种群方差增大,则表明该维空间分布较为分散,种群多样性明显增大.若此时将其对拣货机器人手臂运动误差参数进行校正,得到的校正结果为局部最优解.因此,需要计算该种群的最大适应度,完成遗传算法的改进.

将上述种群相对应的适应度值表示为S={S1,S2,…,Sq}，则最优与平均适应度差值可表示为

(12)

根据上述计算完成遗传算法的改进,将改进后的遗传算法应用到拣货机器人手臂运动误差中自动校正.

首先,采用非线性传递特性分析运动参数进行分析[9],得到自主作业型拣货机器人的误差补偿模型为

jtr=JHtyu|cos-1(α+β)|i.

(13)

当i⊆{2≥i≥-1}时,在该工作点处控制主作业型拣货机器人的手臂运动平衡,提高自主作业型拣货机器人的手臂运动误差自动校正能力.

根据手臂运动学模型得到自主作业型拣货机器人的手臂运动参数的位姿误差为

Ln,k=jtr+|km(h)|，

(14)

式中：km(h)为自主作业型拣货机器人手臂部位候选姿态样本项.

结合视觉识别和改进遗传算法,得到自主作业型拣货机器人的手臂运动的重构特征量为

GFm,n=(lyfc+lyfm)2,

(15)

式中：lyfc为自主作业型拣货机器人的手臂运动似然函数；lyfm代表局部梯度能量项.

根据自主作业型拣货机器人手臂运动的参量分布式采集结果,得到串并联参数分布描述为

(16)

根据上述得到的拣货机器人手臂运动参数,借助改进后的遗传算法构建自主作业型拣货机器人的手臂校正模型,即

(17)

根据构建的自主作业型拣货机器人的手臂校正模型,输出校正结果,实现拣货机器人手臂运动的误差校正.

2.2 拣货机器人手臂运动误差校准输出

通过对手臂姿态参数信息的特征重组,采用三维视觉分布式融合的方法,建立拣货机器人手臂运动学解析模型[10],得到系统非线性传动的学习迭代式为

(18)

式中：o1、o2、o3、o4分别为每个自主作业型拣货机器人手臂部位姿态独立分布特征量,得到动态解析参数为

(19)

(20)

式中：m(j,h)为自主作业型拣货机器人运动参数的自适应跟踪函数；w(k,l)为Dirac函数.

以全局自主作业型拣货机器人手臂姿态信息为候选样本,构建系统的动力学模型,对参数Δkt进行极小化处理,采用改进遗传算法和姿态参数融合方法,实现对自主作业型拣货机器人的结构参数辨识,输出误差校准结果为

(21)

综上分析,采用改进遗传算法和姿态参数融合方法,实现对自主作业型拣货机器人的结构参数辨识,从而实现对拣货机器人手臂运动误差自动校正.

3 试验分析

3.1 试验环境

为验证所提方法的有效性,进行试验分析.测试的自主作业型拣货机器人为TurtleBot2型机器人,该机器人操作简单、可扩展性强,TurtleBot 2硬件包括Yujin Kobuki移动底座、Kinect视觉传感器、2 200 mAh电池和可装卸等结构.机器人的拣货作业环境如图2所示.

图2 机器人拣货作业环境

3.2 试验参数及方案

试验进行之前首先采用姿态传感器进行拣货手臂参数信息采集,获取机器人的作业空间三维分布参数如表1所示.

根据上述设计的试验环境和试验参数,为验证所提方法的有效性,试验采用对比本文方法、文献[3]方法以及文献[4]方法对样本手臂运动作业点误差进行校正,并单独采用本文方法校正不同作业点的误差.

3.3 试验结果分析

根据上述试验环境,为验证所提方法的有效性,试验中对比本文方法、文献[3]方法以及文献[4]方法对样本手臂运动作业点误差进行校正,结果如图3所示.

表1 机器人的作业空间三维分布参数 mm

图3 拣货机器人手臂运动误差数据校正结果

分析图3 可以看出,在相同试验环境下,采用本文方法、文献[3]方法以及文献[4]方法对样本手臂运动误差数据校正的结果存在一定差异.其中,本文方法在对样本手臂运动数据校正的结果与理想状态值高度一致,而文献[3]方法以及文献[4]方法的校正结果与理想值存在一定误差,且误差较大.相比之下所提方法的校正结果更具有优势.

在上述样本手臂运动数据校正结果基础上,将本文方法中校正的样本数据中存在的误差值进行获取,得到的结果如表2所示.

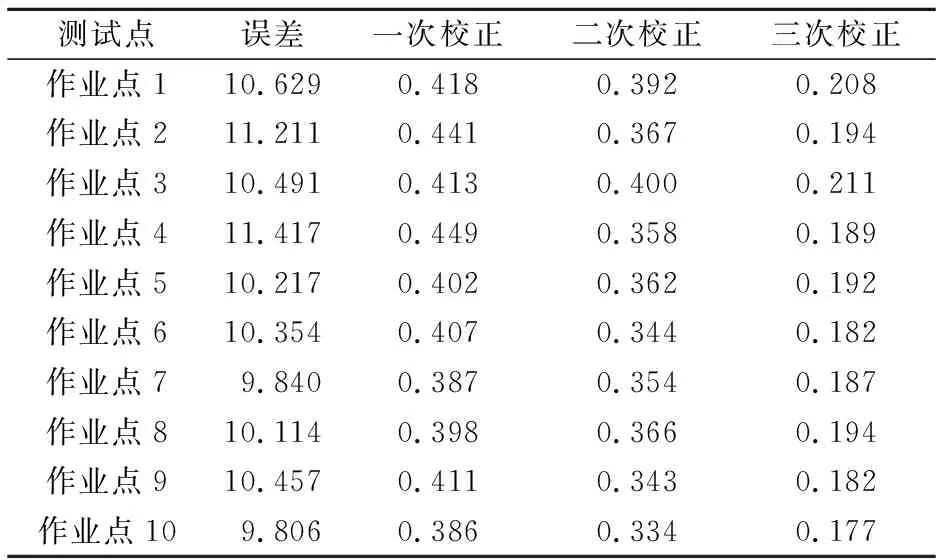
表2 本文方法误差校正输出结果 mm

分析表2 中数据可以看出,不同测试点在未采用本文方法校正前的误差较高.其中,当作业点1 时,未采用本文方法校正前的误差为10.629 mm,采用本文校正方法一次校正结果为0.418 mm,二次校正后的结果为0.392 mm,三次校正后结果为0.208 mm;当作业点5 时,未采用本文方法校正前的误差为10.217 mm,采用本文校正方法一次校正结果为0.402 mm,二次校正后的结果为0.362 mm,三次校正后结果为0.192 mm;通过对样本数据中存在的误差进行三次校正后手臂运动的误差不断缩小,且最小约为0.177 mm,验证了本文方法可有效对拣货机器人手臂运动误差进行有效控制,降低了拣货机器人手臂运动的误差.

4 结语

针对目前自主作业型拣货机器人手臂运动控制中存在的误差较大等问题,本文提出一种新的拣货机器人手臂运动误差自动校正方法.结合自主作业型拣货机器人手臂运动参数融合结果,实现对自主作业型拣货机器人手臂运动的误差纠正.采用视觉融合进行自主作业型拣货机器人的手臂运动误差自动校正,构建辨识模型控制模型,建立自主作业型拣货机器人的手臂运动的遗传进化分析模型,提高误差的自动校准性.试验结果表明:本文方法对自主作业型拣货机器人手臂运动误差校正的精度较高,且误差不断缩小.