基于Ansys的钢筋混凝土框架结构非线性有限元分析
2022-01-05祖庆芝
祖庆芝
(漳州职业技术学院 建筑工程学院 ,福建 漳州 363000)
钢筋混凝土是由钢筋和混凝土2种材料组成的,钢筋混凝土的出现有效推动我国国民经济的发展.由于钢筋混凝土的拉力和承受力较高,使其广泛应用建筑行业中[1-2].
由于钢筋混凝土结构是一种特殊的复合材料,复杂性和特殊性较强,同时现阶段有关于钢筋混凝土框架结构的分析研究受到了环境以及人为等多重因素的干扰,想要精确分析组成结构具有较大的难度.考虑到这些比较复杂的因素,需要精确分析钢筋混凝土结构从加载到破坏的全过程是十分困难的.针对上述问题,国内外相关专家进行了大量的研究.宁可等[3]优先组建箱体三维模型,通过Ansys软件进行有限元分析.鲁亮等[4]通过CR-RCFC摇摆机制和对应节点构建有限元模型,同时对地震作用下的动力时程进行分析,得到不同地震作用下的结构动力特性.在上述已有方法的基础上,本文提出一种基于Ansys的钢筋混凝土框架结构非线性有限元分析方法.仿真实验结果表明,所提方法得到的模拟结果和真实结果更加接近,充分验证了所提方法的有效性和优越性.
1 分析方法
1.1 钢筋混凝土的框架结构分析
1) 破坏曲面.
根据混凝土的破坏准则能够设定满足应力和应变状态的约束条件.
通常情况下,应力状态主要通过坐标{ζ,r,θ}描述,具体如图1所示.将{σ1,σ2,σ3}设定为坐标轴的主应力空间,其中点P{σ1,σ2,σ3}的应力状态可以通过矢量OP代表.
2) 破坏准则.
混凝土的破坏强度和它所在的应力状态存在密切关联.一般情况下,在结构没有受到破坏前期,需要将其设定为同性体,所以破坏准则和坐标之间的选择是不存在任何联系的[5-6],即不需要通过应力状态对应的不变量表示,而是通过{ζ,r,θ}表示,其中对应的破坏准则能够表示为
f{ζ,r,θ,k1,k2,…,kn}=0,
(1)
式中:k1,k2,…,kn为实验确定的主要参数.
3) 破坏模型.
由于钢筋混凝土的真实性和强度是十分复杂的,同时也和多种因素存在关联.研究破坏准则的主要目的就是确定函数的具体表达形式以及实验中各个参数的取值[7-8].

(a)
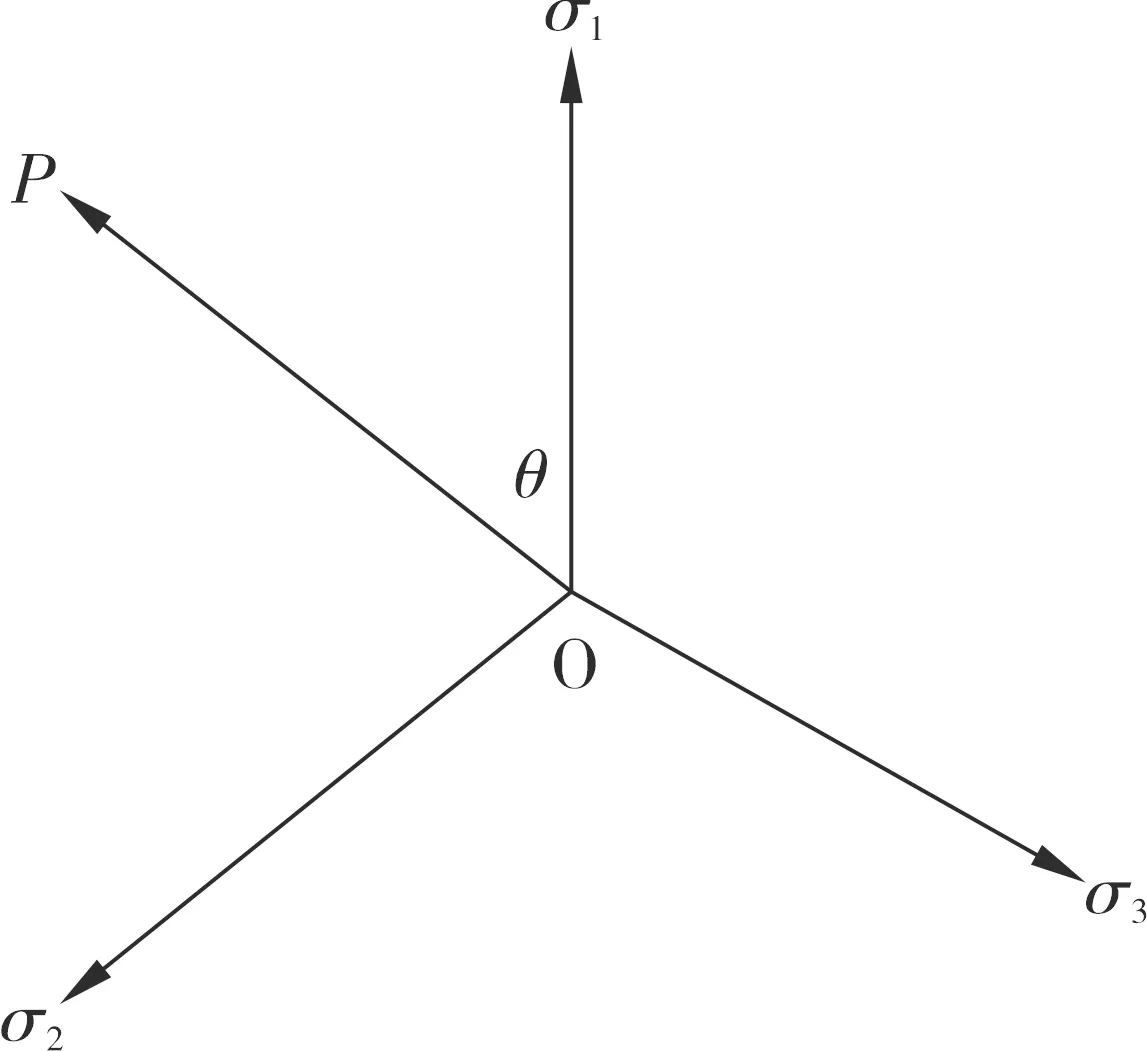
(b)图1 应力状态下的坐标
结合破坏准则中的参数数量,能够将破坏准则划分为单数和双数破坏准则.
1.2 基于Ansys的钢筋混凝土框架结构非线性有限元分析
通过有限元分析软件构建钢筋混凝土框架结构三维实体结构模型,具体的建立流程如图2所示.
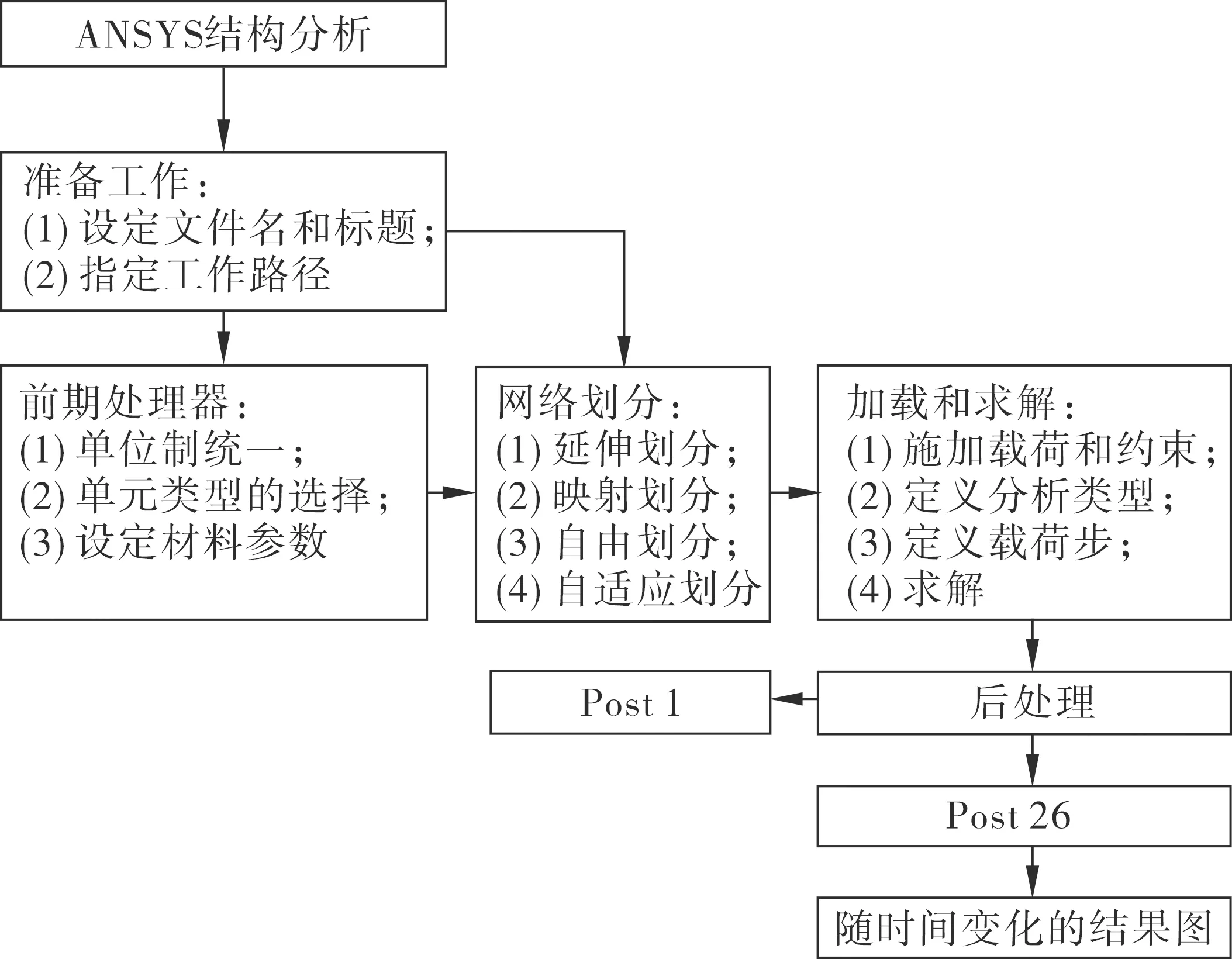
图2 钢筋混凝土框架结构三维实体结构模型构建流程
对钢筋混凝土进行有限元分析的过程中,需要将其中的2种材料进行离散化处理.其中,混凝土占据的比例较大,主要负责承受压力,而钢筋被混凝土包裹在里面,主要负责承受来自各方的拉力.针对钢筋的处理方式,能够将模式划分为3种不同的形式,具体如下所示:
1) 分离式模型.
分离式模型是使用范围比较广的一种模型.在构建模型的初始阶段,需要优先将已有材料划分为规格相同的结构单元.在实际应用钢筋的过程中,不需要考虑横向抗剪强度,结合线性单元进行分析和研究,避免大量数据单元的形成[9].如果钢筋和混凝土之间出现相对滑移的现象,则需要对两者之间的滑移现象进行模拟;否则,则说明其是刚性粘结.
2) 组合式模型.
组合式模型主要被应用于钢筋混凝土框架结构的相对滑移分析[10].
3) 整体式模型.
整体式模型在组建钢筋混凝土模型时,需要结合配筋率进行将钢筋均匀分布在混凝土中,进而推导出2种不同单元的刚度矩阵,具体计算形式如式(2)和式(3)所示.
[K]=[B]T[D][B]dV,
(2)
[D]=[Dc]+[Ds].
(3)
式中:[B]为几何矩阵;[Dc]为混凝土的应变能力矩阵;[Ds]为钢筋的应力应变矩阵.
在模拟钢筋混凝土周围材料时,如果土体为离线的弹性塑料模型[11-12],通过Drucker-Parger屈服准则和关联流动法则.其中,D-P屈服准则对应的等效应力表达式为
(4)
式中:{S}为偏应力;σm为平均应力的取值大小;β为材料常数,主要是由受压和受拉伸屈服应力或者是摩擦角推算出,对应的表达式为
(5)
式中:φ为钢筋混凝土结构内部的摩擦力;C为混凝土的黏度;σt为钢筋能够承受的最大拉伸力;σc为受压屈服应力.
其中,内摩擦角对应的表达式为
(6)
2 钢筋混凝土框架结构实例分析
2.1 实验概况
1) 水泥选取耀县425#普通硅盐酸水泥,砂为河砂,石头为鹅卵石,粒径在15~25 mm.
2) 混凝土配合比.水泥、水、砂、石子的比例为297∶190∶708∶1 025,其中混凝土塌落度控制在30~50 mm.
3) 钢筋选取I级φ10的圆钢,箍筋使用I级φ6的圆钢.
4) 角钢使用25 mm×25 mm×2 mm规格的Q235角钢.
5) 立方体试块的规格为150 mm×150 mm×150 mm,主要分为5批进行浇筑,每批共3块.
6) 钢筋混凝土柱截面为120 mm×120 mm,长度为1 m.
表1给出立体试块的平均强度值.
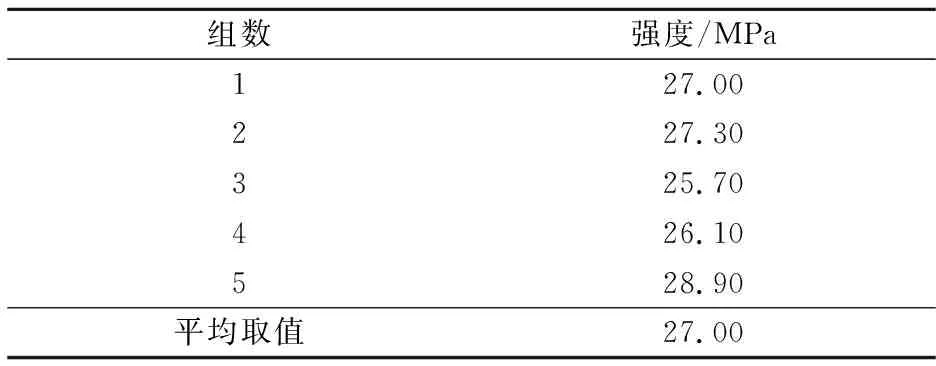
表1 立方体试块平均强度
表2~3给出钢筋和角钢试样的平均屈服强度.
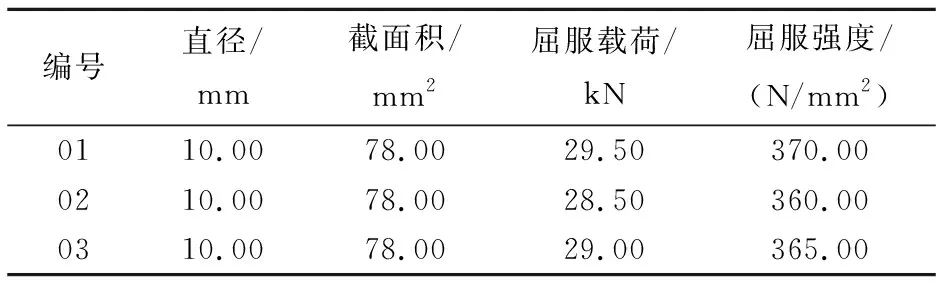
表2 钢筋的平均屈服强度

表3 角钢的平均屈服强度
2.2 实验结果分析
在粘钢加固的过程中,为了方便进行比较分析,设定全部配件的规格相同,具体情况如表4所示.

表4 试件基本情况
分析粘钢加固混凝土梁中的破坏载荷试验值和计算值之间的差值,计算结果如表5所示.
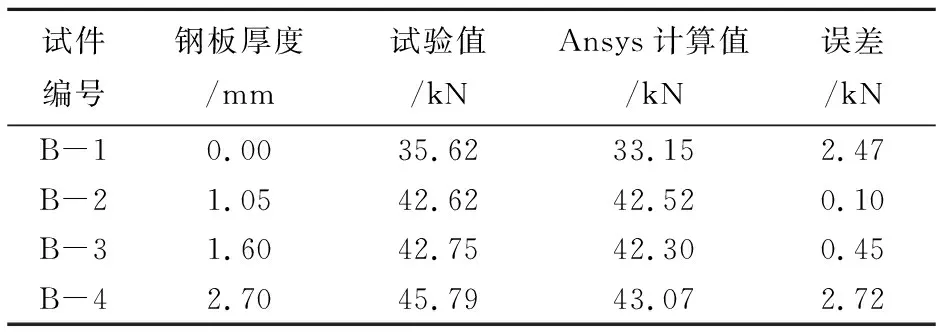
表5 破坏载荷对比结果
分析表5中的实验结果可知:试验值误差结果控制在5 kN内.虽然在实际计算的过程中,粘钢和缓凝体间的位移处于比较和谐的状态,但是整个结构中梁的高度已经远远超出实际情况.同时在实验过程中裂缝开关处于开启状态,会导致混凝土过早产生裂痕,整个钢筋混凝土框架结构的极限载荷取值会明显比实验值更低一些.
分别针对未进行加固和加固粘钢厚度不同的混凝土梁进行有限元分析,得到不同的载荷-挠度曲线如图3所示.

图3 粘钢加固混凝土荷载-挠度曲线对比
3 结论
上述实验数据是通过具体实验测试得到的,通过准确的计算结果,能够得到如下结论:
1) 当对钢筋混凝土粘钢进行加固处理后,整体承载能力得到有效增加,同时跨中挠度也得到了有效控制.
2) 当载荷取值较小时,各梁对应的曲线基本都为线性.
3) 通过加大粘钢厚度能够有效约束跨中挠度,同时当粘钢超过一定的厚度对混凝土承载能力的提升并不显著.
